[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
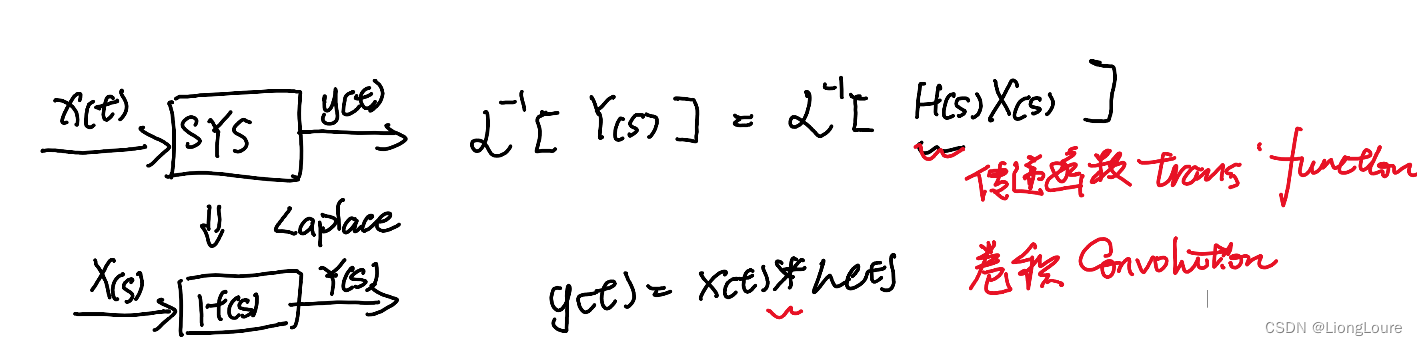
Laplace Transform : X ( s ) = L [ x ( t ) ] = ∫ 0 ∞ x ( t ) e − s t d t X\left( s \right) =\mathcal{L} \left[ x\left( t \right) \right] =\int_0^{\infty}{x\left( t \right) e^{-st}}\mathrm{d}t X(s)=L[x(t)]=∫0∞x(t)e−stdt
Convolution : x ( t ) ∗ g ( t ) = ∫ 0 t x ( τ ) g ( t − τ ) d τ x\left( t \right) *g\left( t \right) =\int_0^t{x\left( \tau \right) g\left( t-\tau \right)}\mathrm{d}\tau x(t)∗g(t)=∫0tx(τ)g(t−τ)dτ
证明: L [ x ( t ) ∗ g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=X(s)G(s)
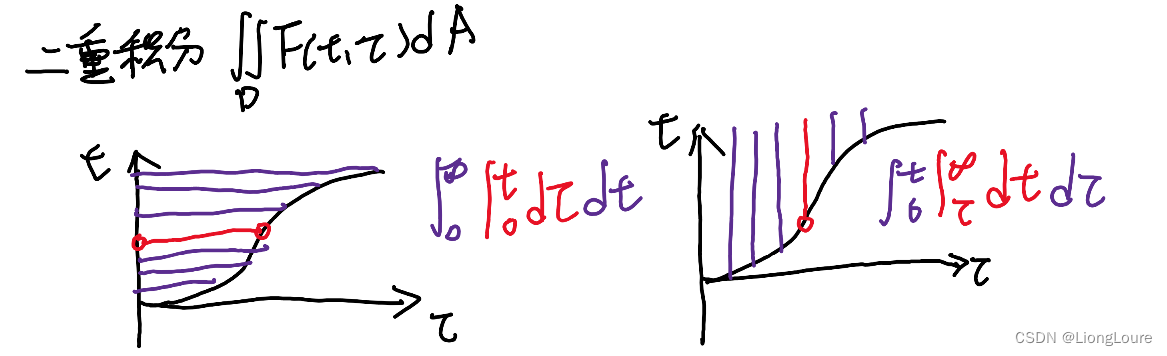
L [ x ( t ) ∗ g ( t ) ] = ∫ 0 ∞ ∫ 0 t x ( τ ) g ( t − τ ) d τ e − s t d t = ∫ 0 ∞ ∫ τ ∞ x ( τ ) g ( t − τ ) e − s t d t d τ \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^t{x\left( \tau \right) g\left( t-\tau \right) \mathrm{d}\tau}e^{-st}}\mathrm{d}t=\int_0^{\infty}{\int_{\tau}^{\infty}{x\left( \tau \right) g\left( t-\tau \right)}e^{-st}}\mathrm{d}t\mathrm{d}\tau L[x(t)∗g(t)]=∫0∞∫0tx(τ)g(t−τ)dτe−stdt=∫0∞∫τ∞x(τ)g(t−τ)e−stdtdτ
>令: u = t − τ , t = u + τ , d t = d u + d τ , t ∈ [ τ , + ∞ ) ⇒ u ∈ [ 0 , + ∞ ) u=t-\tau ,t=u+\tau ,\mathrm{d}t=\mathrm{d}u+\mathrm{d}\tau ,t\in \left[ \tau ,+\infty \right) \Rightarrow u\in \left[ 0,+\infty \right) u=t−τ,t=u+τ,dt=du+dτ,t∈[τ,+∞)⇒u∈[0,+∞)
L [ x ( t ) ∗ g ( t ) ] = ∫ 0 ∞ ∫ 0 ∞ x ( τ ) g ( u ) e − s ( u + τ ) d u d τ = ∫ 0 ∞ x ( τ ) e − s τ d τ ∫ 0 ∞ g ( u ) e − s u d u = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^{\infty}{x\left( \tau \right) g\left( u \right)}e^{-s\left( u+\tau \right)}}\mathrm{d}u\mathrm{d}\tau =\int_0^{\infty}{x\left( \tau \right)}e^{-s\tau}\mathrm{d}\tau \int_0^{\infty}{g\left( u \right)}e^{-su}\mathrm{d}u=X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=∫0∞∫0∞x(τ)g(u)e−s(u+τ)dudτ=∫0∞x(τ)e−sτdτ∫0∞g(u)e−sudu=X(s)G(s)
L [ x ( t ) ∗ g ( t ) ] = L [ x ( t ) ] L [ g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\mathcal{L} \left[ x\left( t \right) \right] \mathcal{L} \left[ g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)∗g(t)]=L[x(t)]L[g(t)]=X(s)G(s)
相关文章:
[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换 Laplace Transform : X ( s ) L [ x ( t ) ] ∫ 0 ∞ x ( t ) e − s t d t X\left( s \right) \mathcal{L} \left[ x\lef…...
生产问题: 利用线程Thread预加载数据缓存,其它类全局变量获取缓存偶发加载不到
生产问题: 利用线程Thread预加载数据缓存偶发加载不到 先上代码 public class ThreadTest {//本地缓存Map<String, Object> map new HashMap<String, Object>();class ThreadA implements Runnable{Overridepublic void run() {System.out.println("Thread…...

Elasticsearch mapping 之 性能相关配置
ES 常见类型 通用类型: 二进制: binary 布尔型: boolean 字符串: keyword, constant_keyword, wildcard, text 别名: alias 对象: object, flattened, nested, join 结构化数据类型: Range, ip, version, murmur3 空间数据类型: geo_point, geo_shape, point, shape 性…...

adb push报错:remote couldn‘t create file: Is a directory
adb push报错:remote couldn‘t create file: Is a directory 出现这个问题可能是电脑本地目录中包含中文或者是目录地址中多包含了一个/ 比如说以下两种路径 1. test/测试音频文件1/a.mp3 2.test/test_audio/ 这两种都是不可以的(我是在as中执行的…...

GitLab 服务更换了机器,IP 地址或域名没有变化时,可能会出现无法拉取或提交代码的情况。
当 GitLab 服务更换了机器,但 IP 地址或域名没有变化时,可能会出现无法拉取或提交代码的情况。 这可能是由于 SSH 密钥或 SSL 证书发生了变化。以下是一些可能的解决步骤: 这可能是由于 SSH 密钥或 SSL 证书发生了变化。以下是一些可能的解决…...

【华为OD题库-076】执行时长/GPU算力-Java
题目 为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。 假设GPU最多一次执行n个任务,一次执行耗时1秒,在保证GPU不空闲情况下&…...

持续集成交付CICD:Jenkins使用GitLab共享库实现前后端项目Sonarqube
目录 一、实验 1.Jenkins使用GitLab共享库实现后端项目Sonarqube 2.优化GitLab共享库 3.Jenkins使用GitLab共享库实现前端项目Sonarqube 4.Jenkins通过插件方式进行优化 二、问题 1.sonar-scanner 未找到命令 2.npm 未找到命令 一、实验 1.Jenkins使用GitLab共享库实现…...
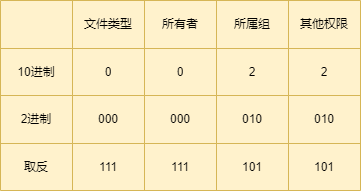
Linux文件结构与文件权限
基于centos了解Linux文件结构 了解一下文件类型 Linux采用的一切皆文件的思想,将硬件设备、软件等所有数据信息都以文件的形式呈现在用户面前,这就使得我们对计算机的管理更加方便。所以本篇文章会对Linux操作系统的文件结构和文件权限进行讲解。 首先…...

CentOS上安装和配置Apache HTTP服务器
在CentOS系统上安装和配置Apache HTTP服务器可以为您的网站提供可靠的托管环境。Apache是开源的Web服务器软件,具有广泛的支持和强大的功能。下面是在CentOS上安装和配置Apache HTTP服务器的步骤: 步骤一:安装Apache HTTP服务器 打开终端&am…...
———ES6迭代器)
前端知识(十二)———ES6迭代器
ES6中的迭代器是一种新的对象,它具有一个next()方法。next()方法返回一个对象,这个对象包含两个属性:value和done。value属性是迭代器中的下一个值,done属性是一个布尔值,表示迭代器是否已经遍历完所有的值。迭代器是一…...
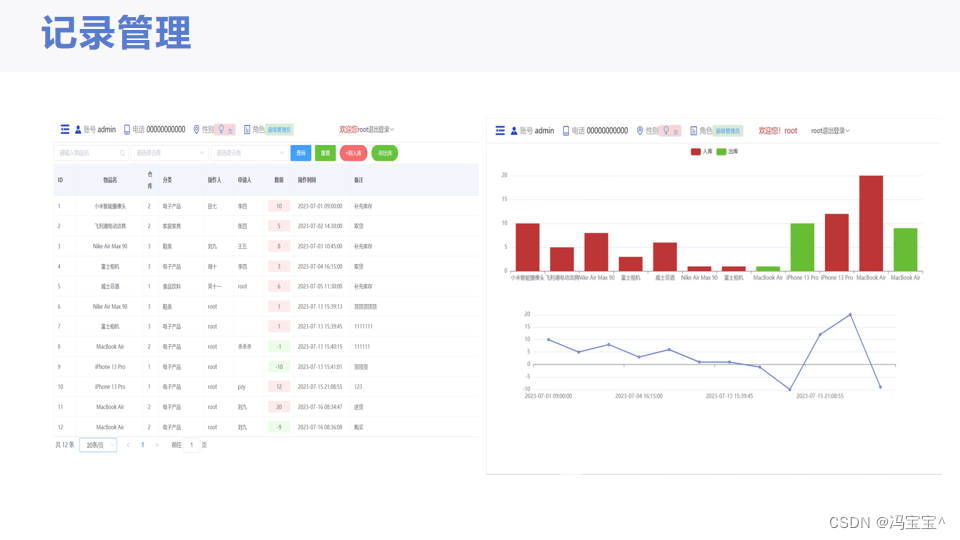
云端仓库平台
SpringBoot MySQL Vue 等技术实现的云端仓库 技术栈 核心框架:SpringBoot 持久层框架:MyBatis-Plus 前端框架:Vue 数据库:MySQL 项目包含源码和数据库文件。 效果图如下:...

php第三方skd自动加载
把mugou-sdk复制到项目下在composer.josn找到classmap加入sdk "autoload": {"classmap": ["mugou-sdk"] },在composer.josn找到files加入sdk "autoload": {"files":[mugou-sdk] },项目目录下运行 composer dump-autoload…...

Golang channle(管道)基本介绍、快速入门
channel(管道)-基本介绍 为什么需要channel?前面使用全局变量加锁同步来解决goroutine的通讯,但不完美 1)主线程在等待所有goroutine全部完成的时间很难确定,我们这里设置10秒,仅仅是估算。 2)如果主线程休眠时间长了,…...

盘点六款颇具潜力的伪原创AI工具
写作作为信息传递的主要媒介,在庞大的信息海洋中,为了在激烈的竞争中脱颖而出,伪原创AI工具成为越来越多写手的神秘利器。在本文中,我们将深入盘点六款颇具潜力的伪原创AI工具,为你揭开它们神秘的面纱。 1. 文心一言 …...
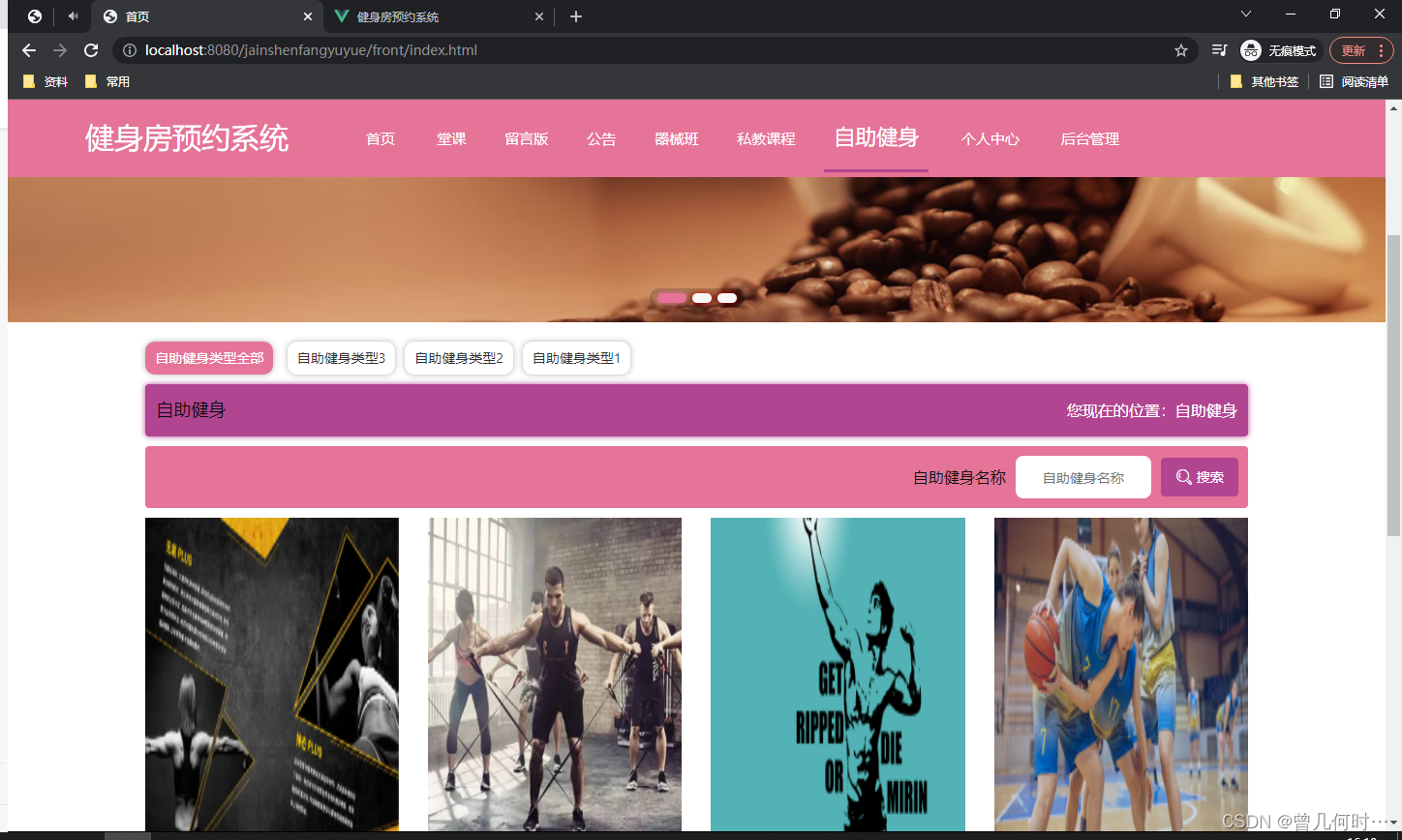
基于SSM的健身房预约系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...
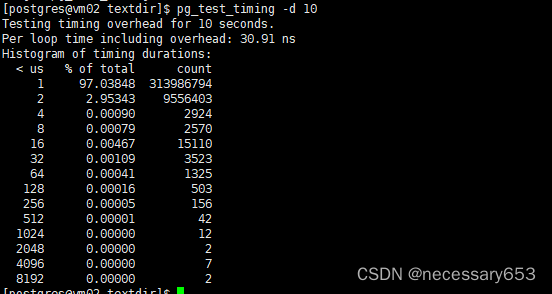
postgresql自带指令命令系列二
简介 在安装postgresql数据库的时候会需要设置一个关于postgresql数据库的PATH变量 export PATH/home/postgres/pg/bin:$PATH,该变量会指向postgresql安装路径下的bin目录。这个安装目录和我们在进行编译的时候./configure --prefix [指定安装目录] 中的prefix参…...
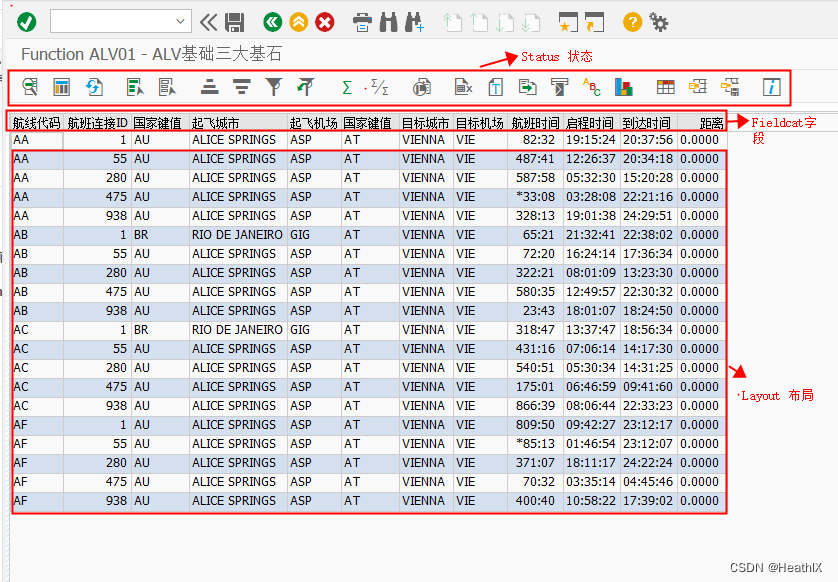
ABAP - Function ALV 02 简单开发一个Function ALV
了解Function ALV: https://blog.csdn.net/HeathlX/article/details/134879766?spm1001.2014.3001.5501程序开发步骤:① TCODE:SE38创建程序 ② 编写程序 DATA gt_spfli TYPE TABLE OF spfli.** Layout 变量定义 (固定使用 直接粘贴复制即可) DATA gs…...

IDEA启动失败报错解决思路
IDEA启动失败报错解决思路 背景:在IDEA里安装插件失败,重启后直接进不去了,然后分析问题解决问题的过程记录下来。方便下次遇到快速解决。也是一种解决问题的思路,分享出去。 启动报错信息 Internal error. Please refer to https…...
密码学学习笔记(二十三):哈希函数的安全性质:抗碰撞性,抗第一原象性和抗第二原象性
在密码学中,哈希函数是一种将任意长度的数据映射到固定长度输出的函数,这个输出通常称为哈希值。理想的哈希函数需要具备几个重要的安全性质,以确保数据的完整性和验证数据的来源。这些性质包括抗碰撞性、抗第一原象性和抗第二原象性。 抗碰…...

STM32-GPIO编程
一、GPIO 1.1 基本概念 GPIO(General-purpose input/output)通用输入输出接口 --GP 通用 --I input输入 --o output输出 通用输入输出接口GPIO是嵌入式系统、单片机开发过程中最常用的接口,用户可以通过编程灵活的对接口进行控制,…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
