【面试常考题目】五种方法解决“如何在n个无序数组中找出它的中位数(java)”问题
1.3 从N个数组中找到中位数,每一个数组可能乱序
在LeetCode上,"寻找多个数组的中位数"这类问题通常是由两个数组合并中位数问题(即LeetCode第4题)的变种或扩展。直接对应于多个数组合并后寻找中位数的题目在LeetCode上并不常见,但是可以通过扩展第4题的解决方案来处理。
处理多个数组合并后寻找中位数的问题,有几种可能的方法:
-
合并后排序:将所有数组合并成一个大数组,然后对这个数组进行排序,最后找到中位数。这种方法简单直接,但如果数组总长度非常大时,可能效率不高。
-
n路归并排序:合并的时候先将各个数组排序,然后采用n路归并的方式不断的将有序值取出(会用到数组指针,每一个元素对应其数组被取出元素的进度),直至取出到总长度的一半,时间复杂度为(n*logx)+O(TL),其中前者为各个数组的排序的时间复杂度之和(假设最长的数组长度为x),后者为这n个数组的总长度。
-
(n路归并的优化)优先队列(堆):使用最小堆(或最大堆)逐个合并数组。每次从堆中取出最小(或最大)元素,直到达到总长度的一半,以此找到中位数。这种方法比直接排序更高效一些。
-
基于快速排序的选择方法(效率最快):基于215. 数组中的第K个最大元素想出来的一种方法,首先需要将n个数组合并,然后对其基于215题进行求解
-
分治+二分法:这是参考LeetCode第4题的一种解决方案。LC第四题是从两个有序数组通过二分找到中位数,那么我们可以先将各个子数组排序,通过分治将数组两两合并成两个大数组,然后再调用LC第四题的方法api完成最终的中位数查找。
尽管LeetCode上可能没有直接对应多个数组合并寻找中位数的题目,上述方法提供了一些处理此类问题的思路。在实际编程挑战或面试中,这些方法可能会派上用场。
1.3.1 合并后排序(略)
1.3.2 合并的时候先将各个数组排序,然后采用n路归并的方式不断的将有序值取出(会用到数组指针,每一个元素对应其数组被取出元素的进度),直至取出到总长度的一半,时间复杂度为(nlogx)+O(n*TL),其中前者为各个数组的排序的时间复杂度之和(假设最长的数组长度为x),后者TL为这n个数组的总长度。
1 详细步骤
您的方法是一个有效的解决方案,它结合了排序和n路归并排序的思想来找到多个数组中的中位数。以下是对您方法的具体分析:
-
先排序:首先对每个数组进行排序。这确保了每个数组内部是有序的,是归并过程中的关键前提。
-
n路归并:利用归并排序的思路,您维护了一个指针数组来追踪每个数组的当前位置。在每一步中,您会从所有数组的当前位置中选出最小的元素,并将相应数组的指针向前移动一位。
-
取出到总长度的一半:由于中位数是位于排序后数组的中间位置,您只需要进行归并操作直到达到所有数组元素总数的一半。这样就可以找到中位数,无需完全归并所有数组。
这种方法的优点是,它避免了对整个合并后的数组进行完整排序,从而减少了不必要的计算,特别是在数据量很大时更有效率。另外,这种方法适用于数组初始时无序的情况,使其成为解决此类问题的一个实用方案。
2 代码实现
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Random;public class Test3 {public static void main(String[] args) {Random random=new Random();List<List<Integer>>list=new ArrayList<>();int n= random.nextInt(5)+1;for (int i = 0; i < n; i++) {int size= random.nextInt(10)+1;List<Integer>tmp=new ArrayList<>();for (int j = 0; j < size; j++) {tmp.add(random.nextInt(100)-50);}list.add(tmp);}for (int i = 0; i < list.size(); i++) {System.out.println("i:"+i+", "+list.get(i).toString());}System.out.println(getMid(list));}static float getMid(List<List<Integer>>list){list.forEach((o)->{Collections.sort(o);});int n= list.size();if(n==0) return 0.0f;int[]ps=new int[n];int tl=0;for (int i = 0; i < n; i++) {tl+=list.get(i).size();}// corner caseif(tl==1)return list.get(0).get(0);int mid=tl/2;int p=0;int preV=Integer.MAX_VALUE,curV=Integer.MAX_VALUE;while(p<mid+1){int minV=Integer.MAX_VALUE,pos=0;//从n个数组中找到最小那一个及其指针for (int i = 0; i < n; i++) {if(ps[i]<list.get(i).size()&&minV>list.get(i).get(ps[i])){minV=list.get(i).get(ps[i]);pos=i;}}ps[pos]++;//更新当前加入数组的值及其前一个有序值preV=curV;curV=minV;p++;}//总长度为偶数时的返回值if(tl%2==1)return preV;return (float) ((preV+curV)/2.0);}
}1.3.3 优先队列(对1.3.2方法的改进):使用一个能装n个元素最小堆逐个合并数组。每次从堆中pop取出最小元素,同时会从pop出的元素所属的数组中再取出一个元素使其填满n个,直到达到总长度的一半,以此找到中位数。这种方法比直接排序更高效一些。
1 详细步骤
使用优先队列(堆)来找到多个数组的中位数是一种高效的方法,特别是当处理多个大型数组时。这种方法的关键在于逐步合并这些数组,同时保持总体的运行效率。以下是具体的步骤和解释:
-
初始化优先队列:首先,创建一个最小堆(或最大堆,取决于具体实现)。优先队列(堆)将用于存储每个数组中的元素,同时保持它们的排序顺序。
-
填充堆:遍历每个数组,将每个数组的第一个元素(假设数组已排序)加入到优先队列中。为了追踪每个元素属于哪个数组以及在其数组中的位置,你可能需要存储额外的信息,比如数组索引和元素索引。
-
逐步取出元素:从优先队列中逐个取出元素。由于优先队列是一个最小堆(或最大堆),每次都能够取出当前所有数组中的最小(或最大)元素。
-
继续填充堆:每当从优先队列中取出一个元素,就从该元素所属的数组中取出下一个元素(如果存在)并将其加入到优先队列中。这样做可以保持堆中始终有所有数组中当前未处理的最小(或最大)元素。
-
找到中位数:重复上述过程,直到从优先队列中取出了总长度一半的元素。此时,取出的最后一个元素(或者最后两个元素的平均值,取决于总长度是奇数还是偶数)就是中位数。
这种方法的时间复杂度主要由优先队列的操作决定,即O(n log k),其中n是所有数组中总元素的数量,k是数组的数量。这比直接合并所有数组后进行排序的O(n log n)更高效,特别是当k远小于n时。此外,这种方法的空间复杂度为O(k),因为优先队列中最多同时包含k个元素。
2 代码实现
import java.util.*;public class Test3 {public static void main(String[] args) {Random random=new Random();List<List<Integer>>list=new ArrayList<>();int n= random.nextInt(2)+1;for (int i = 0; i < 2; i++) {int size= random.nextInt(2)+1;List<Integer>tmp=new ArrayList<>();for (int j = 0; j < size; j++) {tmp.add(random.nextInt(100)-50);}list.add(tmp);}for (int i = 0; i < list.size(); i++) {System.out.println("i:"+i+", "+list.get(i).toString());}System.out.println(getMid(list));}static float getMid(List<List<Integer>>list){list.forEach((o)->{Collections.sort(o);});int n= list.size();if(n==0) return 0.0f;int tl=0;for (int i = 0; i < n; i++) {tl+=list.get(i).size();}// corner caseif(tl==1)return list.get(0).get(0);// entry<arr_id,pos>PriorityQueue<Map.Entry<Integer,Integer>>pq=new PriorityQueue<>((o1,o2)->(list.get(o1.getKey()).get(o1.getValue())-list.get(o2.getKey()).get(o2.getValue())));for (int i = 0; i < n; i++) {pq.offer(new AbstractMap.SimpleEntry<>(i,0));}int mid=tl/2;int p=0;int preV=Integer.MAX_VALUE,curV=Integer.MAX_VALUE;while(p<mid+1){//从n个数组中找到最小那一个及其指针Map.Entry<Integer,Integer>e=pq.poll();int arrId=e.getKey();//属于哪一个数组int pos=e.getValue();//进度指针if(pos+1<list.get(arrId).size()){Map.Entry<Integer,Integer>ne=new AbstractMap.SimpleEntry<>(arrId,pos+1);pq.offer(ne);}//更新当前加入数组的值及其前一个有序值preV=curV;curV=list.get(arrId).get(pos);p++;}if(tl%2==1)return curV;//总长度为偶数时的返回值return (float) ((preV+curV)/2.0);}
}3 时间复杂度:比1.3.2复杂度更低
时间复杂度为(nlogx)+O(log(n)*TL),其中前者为各个数组的排序的时间复杂度之和(假设最长的数组长度为x),TL后者为这n个数组的总长度。
1.3.4 基于快速排序的选择方法
1 思路
参考LC215数组中的第K个最大元素,这个题采用了基于快速排序的选择方法,时间复杂度是O(n),我们知道对于长度为n的数组,n为奇数时,n中位数即是第(n/2+1)小的元素,n为偶数时,n中位数即是第(n/2)小的元素和第(n/2+1)小的元素元素之和的一半。我们知道无论k是多少,最坏的时间复杂度为O(n)
2 代码
假设所有数组的总长度为X,则其时间和空间复杂度均为O(X)
import java.util.*;public class Test3 {public static void main(String[] args) {Random random=new Random();List<List<Integer>>list=new ArrayList<>();int n= random.nextInt(2)+1;for (int i = 0; i < 4; i++) {int size= random.nextInt(2)+1;List<Integer>tmp=new ArrayList<>();for (int j = 0; j < size; j++) {tmp.add(random.nextInt(100)-50);}list.add(tmp);}for (int i = 0; i < list.size(); i++) {System.out.println("i:"+i+", "+list.get(i).toString());}System.out.println(getMid(list));}static float getMid(List<List<Integer>>list){List<Integer>tmp=new ArrayList<>();int n=list.size();//合并所有无序的数组for (int i = 0; i < n; i++) {tmp.addAll(list.get(i));}int mid=tmp.size()/2;if(tmp.size()%2==1){return findK(tmp,mid,0,tmp.size()-1);}else{return (float) ((findK(tmp,mid-1,0,tmp.size()-1)+findK(tmp,mid,0,tmp.size()-1))/2.0);}}// 参考LC215. 数组中的第K个最大元素的解法static int findK(List<Integer>ls, int k, int l, int r){Random random=new Random();int rp= random.nextInt(r-l+1)+l;swap(ls,r,rp);int base=ls.get(r);int low=l,high=r;for (int i = l; i <= high;) {if(ls.get(i)>base){swap(ls,i,high--);}else if(ls.get(i)<base){swap(ls,i++,low++);}else {i++;}}if(k<low){return findK(ls, k,l,low-1);}else if(k>=low&&k<=high){return ls.get(low);}return findK(ls,k,high+1,r);}static void swap(List<Integer>ls, int i, int j){int t=ls.get(i);ls.set(i,ls.get(j));ls.set(j,t);}
}相关文章:
”问题)
【面试常考题目】五种方法解决“如何在n个无序数组中找出它的中位数(java)”问题
1.3 从N个数组中找到中位数,每一个数组可能乱序 在LeetCode上,"寻找多个数组的中位数"这类问题通常是由两个数组合并中位数问题(即LeetCode第4题)的变种或扩展。直接对应于多个数组合并后寻找中位数的题目在LeetCode上…...

打包CSS
接上一个打包HTML继续进行CSS的打包 1.在之前的文件夹里的src文件夹创建一个css文件 2.在浏览器打开webpack——>中文文档——>指南——>管理资源——>加载CSS 3.复制第一句代码到终端 4.复制下图代码到webpack.config.js脚本的plugins:[.....]内容下…...

Java项目开发,业务比较复杂如何减少bug
Java项目开发,业务比较复杂如何减少bug 当Java开发工作涉及复杂业务时,可以采取以下方法来减少bug的数量: 1、深入了解业务需求 充分了解业务需求,与业务人员进行充分的沟通和交流,确保对需求的理解正确。在需求分析…...

[EFI]Atermiter X99 Turbo D4 E5-2630v3电脑 Hackintosh 黑苹果efi引导文件
硬件型号驱动情况主板 Atermiter X99 Turbo D4 处理器 Intel Xeon E5-2630v3 已驱动内存Desktop DDR4 2666 MHz已驱动硬盘Netac NV7000已驱动显卡AMD Radeon RX 5700xt已驱动声卡瑞昱 英特尔 High Definition Audio 控制器ALC897已驱动网卡LucyRTL8125已驱动无线网卡蓝牙Broad…...

map.getOrDefault
map.getOrDefault 是 Java 中的一个方法,用于从 Map 中获取指定键的值,如果键不存在,则返回指定的默认值。 方法签名如下: V getOrDefault(Object key, V defaultValue) 其中,key 是要获取值的键,defaul…...
vue3移动端脚手架(纯净,集成丰富)
概述 一个纯净的移动端框架 ,用到了 Vue3 vuex Vite3 Vant3 sass eslint stylelint htmlhint husky commitlint axios axios-adapter VConsole 自定义全局 loading ,自定义函数式 dialog (api模仿微信小程序)&#x…...
HarmonyOS应用开发-手写板
这是一个基于HarmonyOS做的一个手写板应用,只需要简单的几十行代码,就可以实现如下手写功能以及清空画布功能。 一、先上效果图: 二、上代码 Entry Component struct Index {//手写路径State pathCommands: string ;build() {Column() {//…...

Python中的logging介绍
Python中的logging模块是一个强大的、灵活的、可配置的日志记录系统。它允许你在不修改源代码的情况下记录错误和调试信息,同时也可以对日志信息进行各种处理,例如写入到文件、输出到控制台、记录到数据库等。 logging模块提供了一种用于日志记录的通用接…...
ClickHouse集成JDBC表引擎详细解析)
ClickHouse(17)ClickHouse集成JDBC表引擎详细解析
JDBC 允许CH通过JDBC连接到外部数据库。 要实现JDBC连接,CH需要使用以后台进程运行的程序 clickhouse-jdbc-bridge。 该引擎支持Nullable数据类型。 建表 CREATE TABLE [IF NOT EXISTS] [db.]table_name (columns list... ) ENGINE JDBC(datasource_uri, exte…...
利用CRM系统分析客户行为:精细掌握市场动态
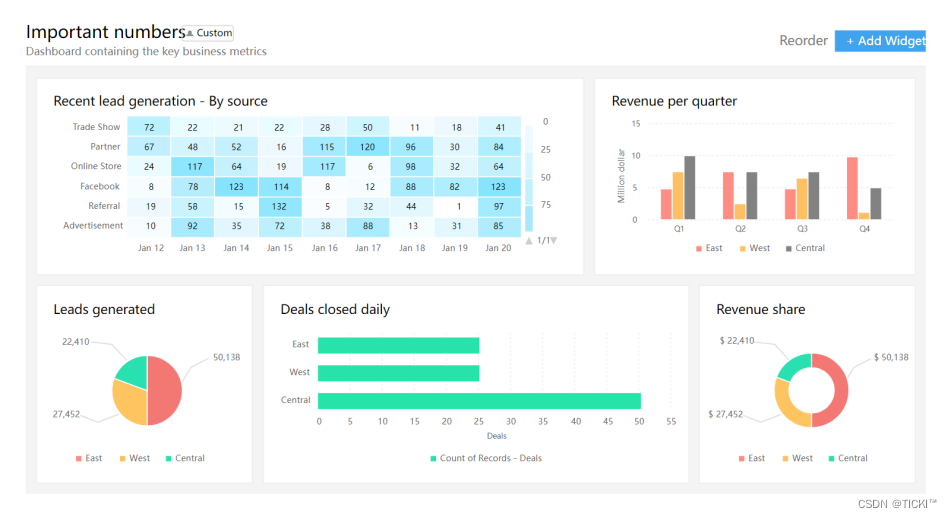
CRM客户关系管理软件在客户行为分析方面发挥着重要作用。通过CRM客户管理系统,企业可以更加便捷地统计客户的行为特征、消费习惯和消费需求,从而洞察市场趋势,帮助企业管理者精准制定营销策略。本文将通过购物篮分析的例子向您介绍CRM客户管理…...
15Linux、GIT及相关相似面试题、PostMan
Linux和git相似是命令相关的层次结构相似 Linux Linux Linux常用操作_linux操作-CSDN博客 程序员常用的10个Linux命令_简介linux系统中的10个常用命令及功能-CSDN博客 help help 命令 :获得 shell 内置命令的帮助信息,常用形式 help cd ls --help …...

游戏中小地图的制作__unity基础开发教程
小地图的制作 Icon标识制作制作摄像机映射创建地图UI效果“不一样的效果” 在游戏中经常可以看到地图视角的存在,那么地图视角是如何让实现的呢? 这一期教大家制作一个简易的小地图。 💖点关注,不迷路。 老样子,我们还…...

sqlite3 --- SQLite 数据库 DB-API 2.0 接口模块
源代码: Lib/sqlite3/ SQLite 是一个C语言库,它可以提供一种轻量级的基于磁盘的数据库,这种数据库不需要独立的服务器进程,也允许需要使用一种非标准的 SQL 查询语言来访问它。一些应用程序可以使用 SQLite 作为内部数据存储。可…...
——如果提高数据样本质量)
做数据分析为何要学统计学(0)——如果提高数据样本质量
样本是数据分析的关键,直接影响研究成果质量。如果样本质量不高,即使使用再好的分析方法,也无法得出理想的结论。所以数据学科圈里有句名言“数据比方法更重要”。所以如何提高数据样本的质量是保证研究成果质量的第一步,虽然这一…...

ubuntu18.04配置cuda+cudnn+tensorrt+anconda+pytorch-gpu+pycharm
一、显卡驱动安装 执行nvidia-smi查看安装情况 二、cuda安装 cuda官网下载cuda_11.6.2_510.47.03_linux.run,安装执行 sudo sh cuda_11.6.2_510.47.03_linux.run提升安装项,驱动不用安装,即第一项(Driver)ÿ…...
C++ 指针常量和常量指针的区别
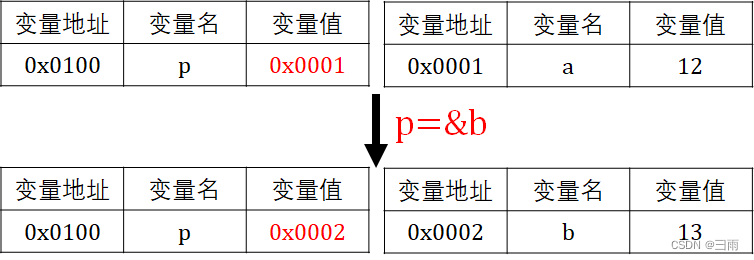
指针常量 指针常量:顾名思义它就是一个常量,但是是指针修饰的。 格式为: int * const p //指针常量在这个例子下定义以下代码: int a,b; int * const p&a //指针常量 //那么分为一下两种操作 *p9;//操…...

如何截取Hive数组中的前N个元素?
文章目录 1、需求描述2、使用索引3、使用posexplode()4、转换为字符串操作 1、需求描述 需求:截取任意给定数组中的前N个元素,返回截取后的子数组 假设我们有如下三种类型的Hive数组: select array(1,2,3,4) -- [1,2,3,4] selec…...
iPaaS架构深入探讨
在数字化时代全面来临之际,企业正面临着前所未有的挑战与机遇。技术的迅猛发展与数字化转型正在彻底颠覆各行各业的格局,不断推动着企业迈向新的前程。然而,这一数字化时代亦衍生出一系列复杂而深奥的难题:各异系统之间数据孤岛、…...
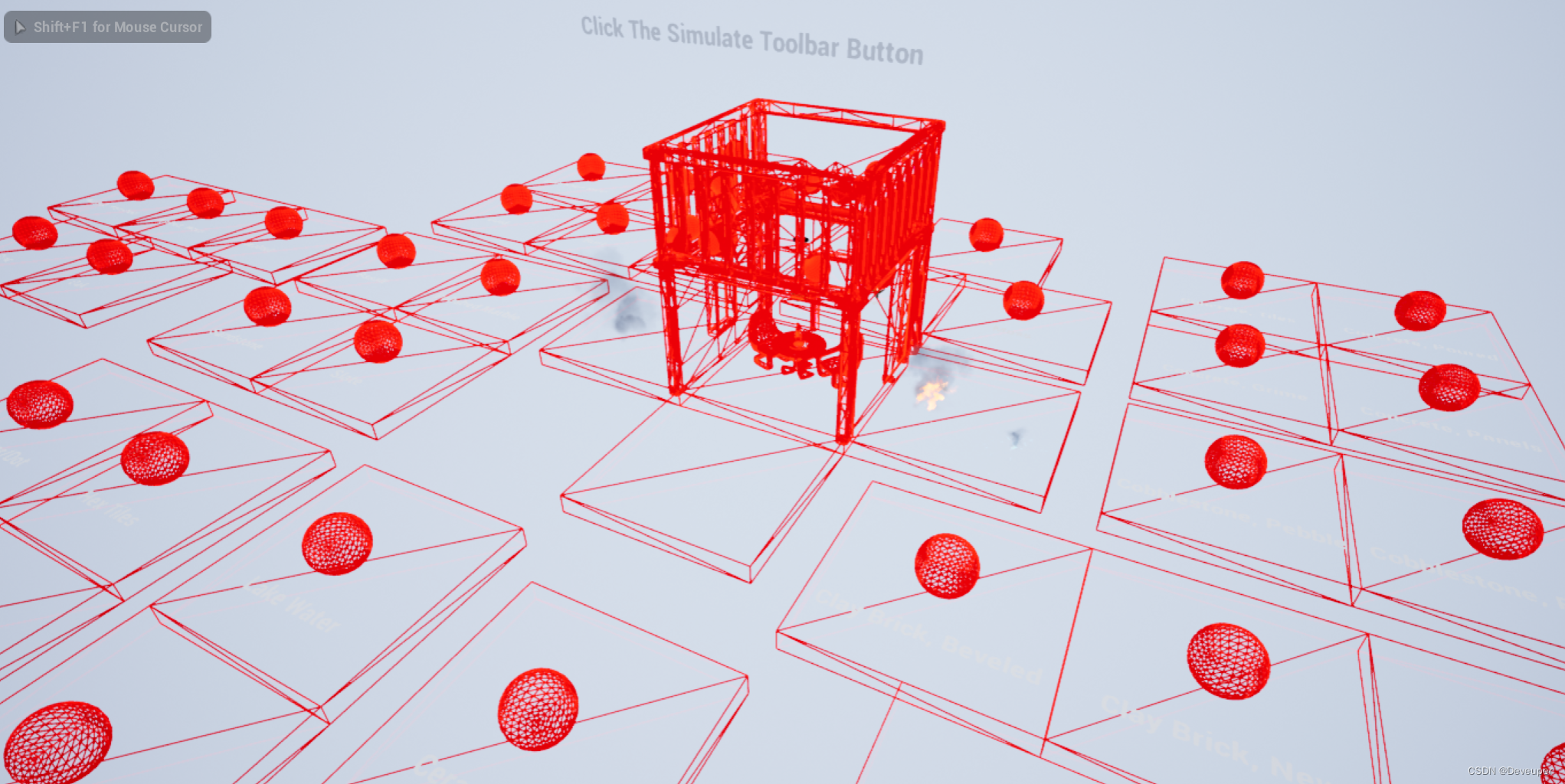
UE4/UE5 修改/还原场景所有Actor的材质
使用蓝图方法: 1.修改场景所有Actor 材质: Wirframe:一个材质类 MatList:获取到的所有模型的全部材质 的列表 TempAllClass:场景中所有获取的 Actor 的列表 功能方法如下: 蓝图代码可复制在:…...
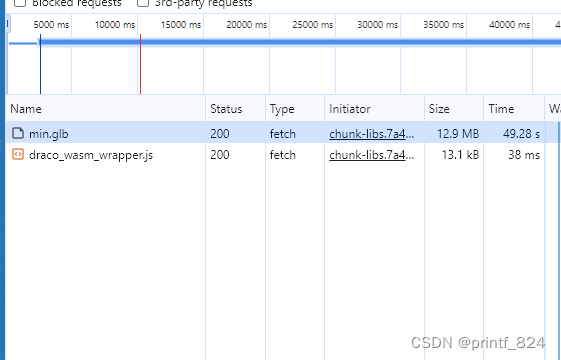
Three.js + Vue 处理glb文件过大问题(DRACOLoader加载压缩glb)
起因,three.js editer导出的glb文件过于庞大,导致部署后文件加载过久 解决方法: 第一步(得有个blender),压缩: 导出时把压缩勾选上 这时候我们会得到一个glb文件,但与three.js edite…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
