【贪心】LeetCode-406. 根据身高重建队列
406. 根据身高重建队列。
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
1 <= people.length <= 2000
0 <= hi <= 10^6
0 <= ki < people.length
题目数据确保队列可以被重建
算法分析
解题思路
- 先排序,h升序,k降序
- 根据k值站位
class Solution {public int[][] reconstructQueue(int[][] people) {//h升序,k降序Arrays.sort(people, (o1,o2) -> o1[0] != o2[0] ? o2[0]- o1[0] : o1[1] - o2[1]);List<int[]> ans = new ArrayList<int[]>();for (int[] person : people) {ans.add(person[1], person);}return ans.toArray(new int[ans.size()][]);}
}
复杂性分析
时间复杂度:O(n2)
空间复杂度:O(logn)
相关文章:

【贪心】LeetCode-406. 根据身高重建队列
406. 根据身高重建队列。 假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。 请你重新…...
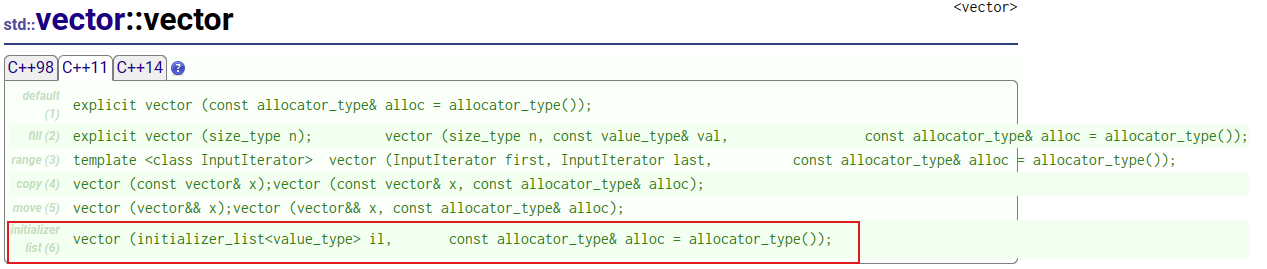
【C++11特性篇】C++11中新增的initializer_list——初始化的小利器
前言 大家好吖,欢迎来到 YY 滴C11系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 主要内容含: 欢迎订阅 YY滴C专栏!更多干货持续更新!以下是传送门! 目录 一.探究std::initializer_list是什么…...

springboot(ssm宠物美容机构CRM系统 宠物服务商城系统Java系统
springboot(ssm宠物美容机构CRM系统 客户关系管理系统Java系统 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0ÿ…...

LSTM 双向 Bi-LSTM
目录 一.Bi-LSTM介绍 二.Bi-LSTM结构 Bi-LSTM 代码实例 一.Bi-LSTM介绍 由于LSTM只能从序列里由前往后预测,为了既能够从前往后预测,也能从后往前预测,Bi-LSTM便被发明了出来。简单来说,BiLSTM就是由前向LSTM与后向LSTM组合而成。 二.Bi-LSTM结构 转自:...

2024测试开发面试题完整版本(附答案)
目录 1. 什么是软件测试, 谈谈你对软件测试的了解 2. 我看你简历上有写了解常见的开发模型和测试模型, 那你跟我讲一下敏捷模型 3. 我看你简历上还写了挺多开发技能的, 那你给我讲讲哈希表的实现流程 4. 谈一谈什么是线程安全问题, 如何解决 5. 既然你选择走测…...
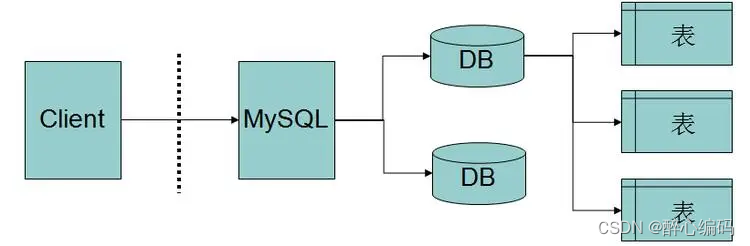
MySQL作为服务端的配置过程与实际案例
MySQL是一款流行的关系型数据库管理系统,广泛应用于各种业务场景中。作为服务端,MySQL的配置过程对于数据库的性能、安全性和稳定性至关重要。本文将详细介绍MySQL作为服务端的配置过程,并通过一个实际案例进行举例说明。 一、MySQL服务端配…...

Appium 自动化自学篇 —— 初识Appium自动化!
Appium 简介 随着移动终端的普及,手机应用越来越多,也越来越重要。而作为测试 的我们也要与时俱进,努力学习手机 App 的相关测试,文章将介绍手机自动化测试框架 Appium 。 那究竟什么是 Appium 呢? 接下来我们一起来学习PythonS…...
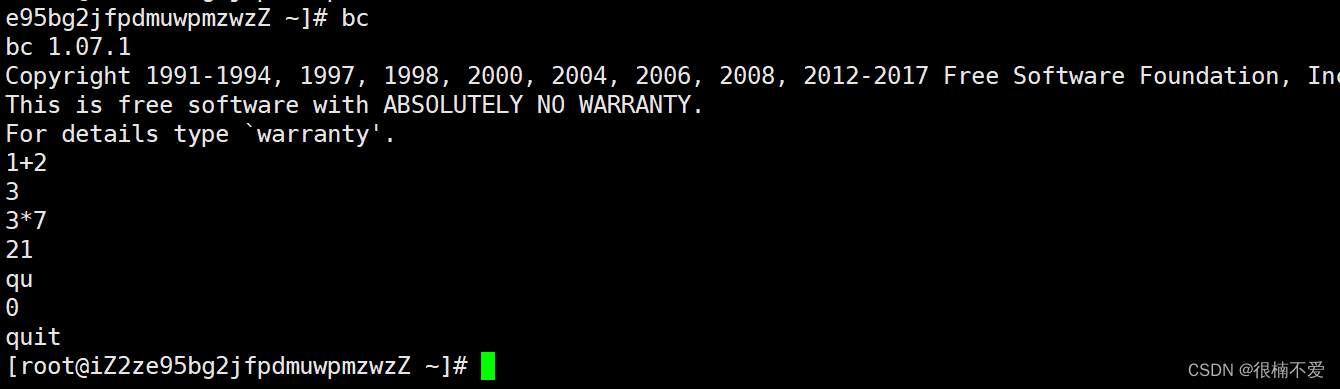
Linux基本操作指令
哈喽小伙伴们,从这篇文章开始,在学习数据结构的同时,我们开启一个新的篇章——Linux操作系统的学习,这将会是又一个新的开始,希望小伙伴们能够认真细心,不要掉队哦。 目录 一.什么是Linux 二.为什么要学习…...

探索SD-WAN技术对传统制造业实现智能制造的作用
在智能制造背景下,传统制造业面临着日益增长的信息化建设需求。随着企业趋向数字化转型,构建稳定、高效的网络基础设施成为提升企业核心竞争力的重要一环。 制造业企业信息化建设中的组网需求: 第一,连接多地分支机构,…...

C++基础-this指针详解
本文详细讲解C++this指针 定义 this 是 C++ 中的一个关键字,一个特殊的指针,它指向当前对象地址(换句话说,其值为 &object),通过它可以访问当前对象的所有成员。 类定义好后我们就可以通过类来创建多个实例对象,每个对象都有各自的实例属性(实例变量),但是非内…...
如何一键生成多个文件二维码?批量文件二维码制作技巧
文件能批量生成二维码吗?现在的二维码用途范围越来越广,比如常见的有图文、文件、问卷、音频或者视频等内容生成二维码图片,扫码查看内容。那么当需要将很多的文件每个都单独生成一个二维码时,有没有比较简单快捷的操作方法吗&…...

SQL连续
SQL连续 1、连续概述2、SQL连续及应用2.1、静态连续2.2、动态连续1、连续概述 连续问题是实际数据开发中比较常见的场景。例如,统计用户连续活跃天数等 SQL如何解决连续问题?本文主要介绍连续性问题,重点以常见的连续活跃场景为例,抽象出通用的连续问题解决方案。连续问题…...

sql server导出与导入
解决:不同版本sql server复制表、导数据;把数据库的结构和全部数据从2016版导入到2014版。 分离数据为mdf,ldf后,导入过程中无权限、被占用问题。 文章目录 使用脚本(.sql文件)导出导入备注 使用mdf,mlf导…...
DevEco Studio 项目鸿蒙(HarmonyOS)资源引用(自定统和系统)
DevEco Studio 项目鸿蒙(HarmonyOS)资源引用(自定统和系统) 一、操作环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、资源访问 HarmonyOS应用资源分为两类,一类是应用资源&…...

使用国内镜像源安装opencv
在控制台输入命令: pip install opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple 验证安装: step 1: 打开终端;step 2: 输入python,进入Python编译环境;step 3: 粘贴…...
人工智能与大数据的紧密联系
随着科技的飞速发展,人工智能(Artificial Intelligence,AI)和大数据(Big Data)已成为当今社会的热门话题。人工智能在许多领域的应用越来越广泛,而大数据则提供了支持和驱动AI技术的巨大资源。本…...

macbookpro 2024怎么恢复出厂设置
可能你的MacBook曾经是高性能的代表,但是现在它正慢慢地逝去了自己的光芒?随着逐年的使用以及文件的添加和程序的安装,你的MacBook可能会开始变得迟缓卡顿,或者失却了以往的光彩。如果你发现你的Mac开始出现这些严重问题ÿ…...

Linux系统编程(二):标准 I/O 库(下)
参考引用 UNIX 环境高级编程 (第3版)嵌入式Linux C应用编程-正点原子 1. 标准 I/O 库简介 标准 I/O 库是指:标准 C 库中用于文件 I/O 操作(如:读、写文件等)相关的一系列库函数的集合 标准 I/O 库函数相关的函数定义都在头文件 &…...
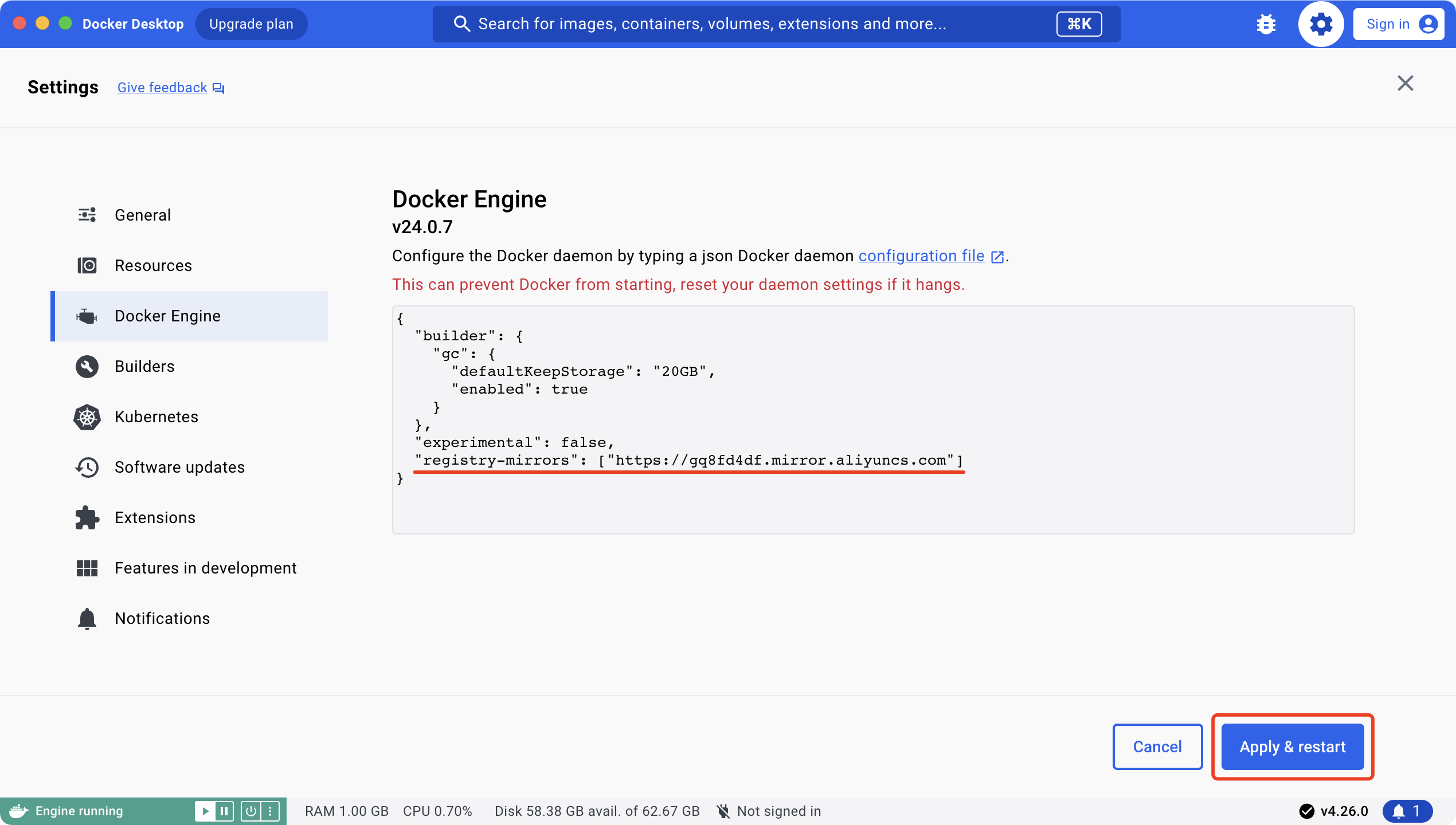
Mr. Cappuccino的第65杯咖啡——MacOS安装Docker
MacOS安装Docker 下载Docker安装Docker查看Docker相关信息镜像加速 下载Docker Docker官网 Docker文档中心 Docker桌面版下载地址 安装Docker 查看Docker相关信息 docker --versiondocker info镜像加速 阿里云镜像加速器 "registry-mirrors": ["https://gq8…...
)
解决 Docker Hub 国内无法访问的方法(Docker 镜像下载加速)
参考文章: 知乎:解决目前Docker Hub国内无法访问方法汇总 docker配置 修改配置文件 vim /etc/docker/daemon.json配置内容如下: {"builder": {"gc": {"defaultKeepStorage": "20GB","enab…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
