拓扑排序实现循环依赖判断 | 京东云技术团队
本文记录如何通过拓扑排序,实现循环依赖判断
前言
一般提到循环依赖,首先想到的就是Spring框架提供的Bean的循环依赖检测,相关文档可参考:
https://blog.csdn.net/cristianoxm/article/details/113246104
本文方案脱离Spring Bean的管理,通过算法实现的方式,完成对象循环依赖的判断,涉及的知识点包括:邻接矩阵图、拓扑排序、循环依赖。本文会着重讲解技术实现,具体算法原理不再复述
概念释义
1. 什么是邻接矩阵?
这里要总结的邻接矩阵是关于图的邻接矩阵;图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图;一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息;
图分为有向图和无向图,其对应的邻接矩阵也不相同,无向图的邻接矩阵是一个对称矩阵,就是一个对称的二位数组,a[i][j] = a[j][i];
邻接矩阵可以清楚的知道图的任意两个顶点是否有边;方便计算任意顶点的度(包括有向图的出度和入度);可以直观的看出任意顶点的邻接点;
本案例中,有向邻接矩阵图为进行拓扑排序的必要条件之一,其次为有向邻接矩阵图每个顶点的入度
2. 邻接矩阵的存储结构?
vexs[MAXVEX]这是顶点表;
arc[MAXVEX][MAXVEX]这是邻接矩阵图,也是存储每条边信息的二维数组。数组的索引是边的两个顶点,数组的数据是边的权值;
numVertexes, numEdges分别为图的顶点数和边数。
3. 有向邻接矩阵图顶点的入度?
在有向图中,箭头是具有方向的,从一个顶点指向另一个顶点,这样一来,每个顶点被指向的箭头个数,就是它的入度。从这个顶点指出去的箭头个数,就是它的出度
邻接矩阵的行号即代表箭头的出发结点,列号是箭头的指向结点,所以矩阵中同一行为1的表示有从第i个结点指向第j个结点这样一条边,而在同列为1就代表第j个结点被第i个结点指向,因此要求顶点的入度或出度,只需要判断同列为1的个数或同行为1的个数
4. 什么是拓扑排序?
拓扑排序的要素:
1.有向无环图;
2.序列里的每一个点只能出现一次;
3.任何一对 u 和 v ,u 总在 v 之前(这里的两个字母分别表示的是一条线段的两个端点,u 表示起点,v 表示终点);
根据拓扑排序的要素,可通过其有向无环来判断对象依赖是否存在循环。若对象组成的图可完成拓扑排序,则该对象图不存在环,即对象间不存在循环依赖。
拓扑排序除了通过有向邻接矩阵图实现外,还可以通过深度优先搜索(DFS)来实现。本案例中仅讲解前者。
5. 什么是循环依赖?
简单解释如下,若存在两个对象,若A创建需要B,B创建需要A,这两个对象间互相依赖,就构成了最简单的循环依赖关系。
编程示例
1. 对象实体
@Builder
@NoArgsConstructor
@AllArgsConstructor
@Getter
@Setter
@ToString
public class RelationVo implements Serializable {/*** 唯一标识*/private String uniqueKey;/*** 关联唯一标识集合*/private List combinedUniqueKeys;}2. 对象集合转换为有向邻接矩阵图
/*** 将List集合转换为邻接矩阵图的二维数组形式** @param sourceList* @return*/public static int[][] listToAdjacencyMatrixDiagram(List sourceList) {List distinctRelationVoList = new ArrayList(sourceList);List keyCollect = distinctRelationVoList.stream().map(RelationVo::getUniqueKey).collect(Collectors.toList());for (RelationVo vo : sourceList) {vo.getCombinedUniqueKeys().forEach(child -> {if (!keyCollect.contains(child)) {// 若叶子节点不在集合中,补充List集合中单独叶子节点,目的是完成提供邻接矩阵图计算的入参keyCollect.add(child);RelationVo build = RelationVo.builder().uniqueKey(child).build();distinctRelationVoList.add(build);}});}// 顶点数:对象中出现的全部元素总数int vertexNum = keyCollect.size();/** 初始化邻接矩阵图的边的二维数组,1表示有边 0表示无边 权重均为1* 其中数组下标为边的两个顶点,数组值为对象边的权值(权值=是否有边*权重)*/int[][] edges = new int[vertexNum][vertexNum];// 计算邻接矩阵图for (int i = 0; i < vertexNum; i++) {RelationVo colVo = distinctRelationVoList.get(i);List colUniqueKeys = colVo.getCombinedUniqueKeys();for (int j = 0; j < vertexNum; j++) {RelationVo rowVo = distinctRelationVoList.get(j);String rowVertex = rowVo.getUniqueKey();if (CollUtil.isNotEmpty(colUniqueKeys)) {if (colUniqueKeys.contains(rowVertex)) {edges[i][j] = 1;} else {edges[i][j] = 0;}}}}return edges;}3. 计算邻接矩阵图顶点的入度
/*** 返回给出图每个顶点的入度值** @param adjMatrix 给出图的邻接矩阵值* @return*/public static int[] getSource(int[][] adjMatrix) {int len = adjMatrix[0].length;int[] source = new int[len];for (int i = 0; i < len; i++) {// 若邻接矩阵中第i列含有m个1,则在该列的节点就包含m个入度,即source[i] = mint count = 0;for (int j = 0; j < len; j++) {if (adjMatrix[j][i] == 1) {count++;}}source[i] = count;}return source;}4. 对邻接矩阵图进行拓扑排序
/*** 拓扑排序,返回给出图的拓扑排序序列* 拓扑排序基本思想:* 方法1:基于减治法:寻找图中入度为0的顶点作为即将遍历的顶点,遍历完后,将此顶点从图中删除* 若结果集长度等于图的顶点数,说明无环;若小于图的顶点数,说明存在环** @param adjMatrix 给出图的邻接矩阵值* @param source 给出图的每个顶点的入度值* @return*/public static List topologySort(int[][] adjMatrix, int[] source) {// 给出图的顶点个数int len = source.length;// 定义最终返回路径字符数组List result = new ArrayList(len);// 获取入度为0的顶点下标int vertexFound = findInDegreeZero(source);while (vertexFound != -1) {result.add(vertexFound);// 代表第i个顶点已被遍历source[vertexFound] = -1;for (int j = 0; j < adjMatrix[0].length; j++) {if (adjMatrix[vertexFound][j] == 1) {// 第j个顶点的入度减1source[j] -= 1;}}vertexFound = findInDegreeZero(source);}//输出拓扑排序的结果return result;}/*** 找到入度为0的点,如果存在入度为0的点,则返回这个点;如果不存在,则返回-1** @param source 给出图的每个顶点的入度值* @return*/public static int findInDegreeZero(int[] source) {for (int i = 0; i < source.length; i++) {if (source[i] == 0) {return i;}}return -1;}5. 检查集合是否存在循环依赖
/*** 检查集合是否存在循环依赖** @param itemList*/public static void checkCircularDependency(List itemList) throws Exception {if (CollUtil.isEmpty(itemList)) {return;}// 计算邻接矩阵图的二维数组int[][] edges = listToAdjacencyMatrixDiagram(itemList);// 计算邻接矩阵图每个顶点的入度值int[] source = getSource(edges);// 拓扑排序得到拓扑序列List topologySort = topologySort(edges, source);if (source.length == topologySort.size()) {// 无循环依赖return;} else {// 序列集合与顶点集合大小不一致,存在循环依赖throw new Exception("当前险种关系信息存在循环依赖,请检查");}}单测用例
1. 测试物料-无循环依赖
示例JSON Array结构(可完成拓扑排序):
[{"uniqueKey":"A","combinedUniqueKeys":["C","D","E"]
},
{"uniqueKey":"B","combinedUniqueKeys":["D","E"]
},
{"uniqueKey":"D","combinedUniqueKeys":["C"]
}
]2. 测试物料-存在循环依赖
示例JSON Array结构(不可完成拓扑排序):
[{"uniqueKey":"A","combinedUniqueKeys":["C","D","E"]
},
{"uniqueKey":"B","combinedUniqueKeys":["D","E"]
},
{"uniqueKey":"D","combinedUniqueKeys":["C"]
},
{"uniqueKey":"C","combinedUniqueKeys":["B"]
}
]3. 单测示例
@Slf4j
public class CircularDependencyTest {/*** 针对集合信息判断该集合是否存在循环依赖*/@Testvoid testCircularDependencyList() throws Exception {String paramInfo = "[{\"uniqueKey\":\"A\",\"combinedUniqueKeys\":[\"C\",\"D\",\"E\"]},{\"uniqueKey\":\"B\",\"combinedUniqueKeys\":[\"D\",\"E\"]},{\"uniqueKey\":\"D\",\"combinedUniqueKeys\":[\"C\"]}]";// 序列化List list = JSONArray.parseArray(paramInfo, RelationVo.class);TopologicalSortingUtil.checkCircularDependency(list);}
}作者:京东保险 侯亚东
来源:京东云开发者社区 转载请注明来源
相关文章:

拓扑排序实现循环依赖判断 | 京东云技术团队
本文记录如何通过拓扑排序,实现循环依赖判断 前言 一般提到循环依赖,首先想到的就是Spring框架提供的Bean的循环依赖检测,相关文档可参考: https://blog.csdn.net/cristianoxm/article/details/113246104 本文方案脱离Spring Be…...
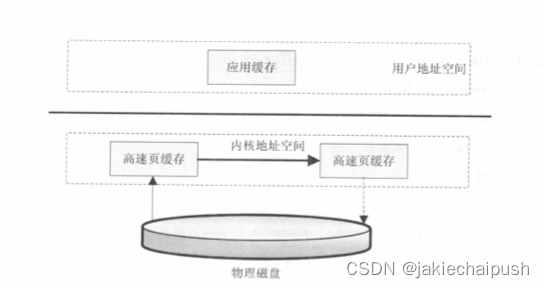
Java的NIO工作机制
文章目录 1. 问题引入2. NIO的工作方式3. Buffer的工作方式4. NIO数据访问方式 1. 问题引入 在网络通信中,当连接已经建立成功,服务端和客户端都会拥有一个Socket实例,每个Socket实例都有一个InputStream和OutputStream,并通过这…...

一个简单的光线追踪渲染器
前言 本文参照自raytracing in one weekend教程,地址为:https://raytracing.github.io/books/RayTracingInOneWeekend.html 什么是光线追踪? 光线追踪模拟现实中的成像原理,通过模拟一条条直线在场景内反射折射,最终…...
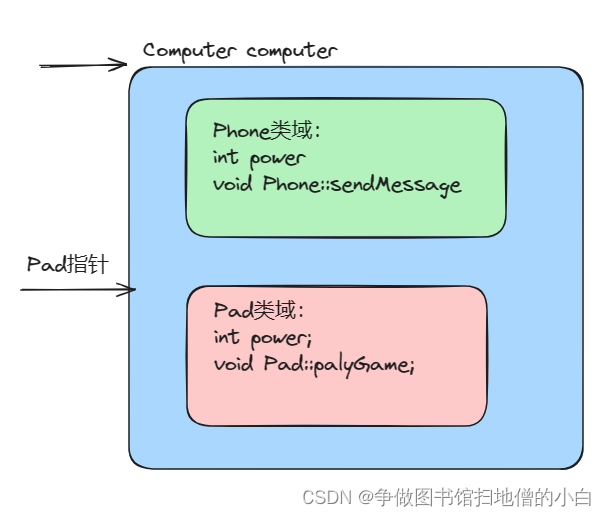
C++学习笔记(十二)------is_a关系(继承关系)
你好,这里是争做图书馆扫地僧的小白。 个人主页:争做图书馆扫地僧的小白_-CSDN博客 目标:希望通过学习技术,期待着改变世界。 提示:以下是本篇文章正文内容,下面案例可供参考 文章目录 前言 一、继承关系…...

DC电源模块的设计与制造技术创新
BOSHIDA DC电源模块的设计与制造技术创新 DC电源模块的设计与制造技术创新主要涉及以下几个方面: 1. 高效率设计:传统的DC电源模块存在能量转换损耗较大的问题,技术创新可通过采用高效率的电路拓扑结构、使用高性能的功率开关器件和优化控制…...

Sketch for Mac:实现你的创意绘图梦想的矢量绘图软件
随着数字时代的到来,矢量绘图软件成为了广告设计、插画创作和UI设计等领域中必不可少的工具。在众多矢量绘图软件中,Sketch for Mac(矢量绘图软件)以其强大的功能和简洁的界面脱颖而出,成为了众多设计师的首选。 Sket…...

ReactNative0.73发布,架构升级与更好的调试体验
这次更新包含了多种提升开发体验的改进,包括: 更流畅的调试体验: 通过 Hermes 引擎调试支持、控制台日志历史记录和实验性调试器,让调试过程更加高效顺畅。稳定的符号链接支持: 简化您的开发工作流程,轻松将文件或目录链接到其他…...

SVN忽略文件的两种方式
当使用版本管理工具时,提交到代码库的文档我们不希望存在把一些临时文件也推送到仓库中,这样就需要用到忽略文件。SVN的忽略相比于GIT稍显麻烦,GIT只需要在.gitignore添加忽略规则即可。而SVN有两种忽略方式,一个是全局设置&#…...

手写VUE后台管理系统10 - 封装Axios实现异常统一处理
目录 前后端交互约定安装创建Axios实例拦截器封装请求方法业务异常处理 axios 是一个易用、简洁且高效的http库 axios 中文文档:http://www.axios-js.com/zh-cn/docs/ 前后端交互约定 在本项目中,前后端交互统一使用 application/json;charsetUTF-8 的请…...

JavaScript装饰者模式
JavaScript装饰者模式 1 什么是装饰者模式2 模拟装饰者模式3 JavaScript的装饰者4 装饰函数5 AOP装饰函数6 示例:数据统计上报 1 什么是装饰者模式 在程序开发中,许多时候都我们并不希望某个类天生就非常庞大,一次性包含许多职责。那么我们就…...

C++学习笔记01
01.C概述(了解) c语言在c语言的基础上添加了面向对象编程和泛型编程的支持。 02.第一个程序helloworld(掌握) #define _CRT_SECURE_NO_WARNINGS #include<iostream> using namespace std;//标准命名空间int main() {//co…...
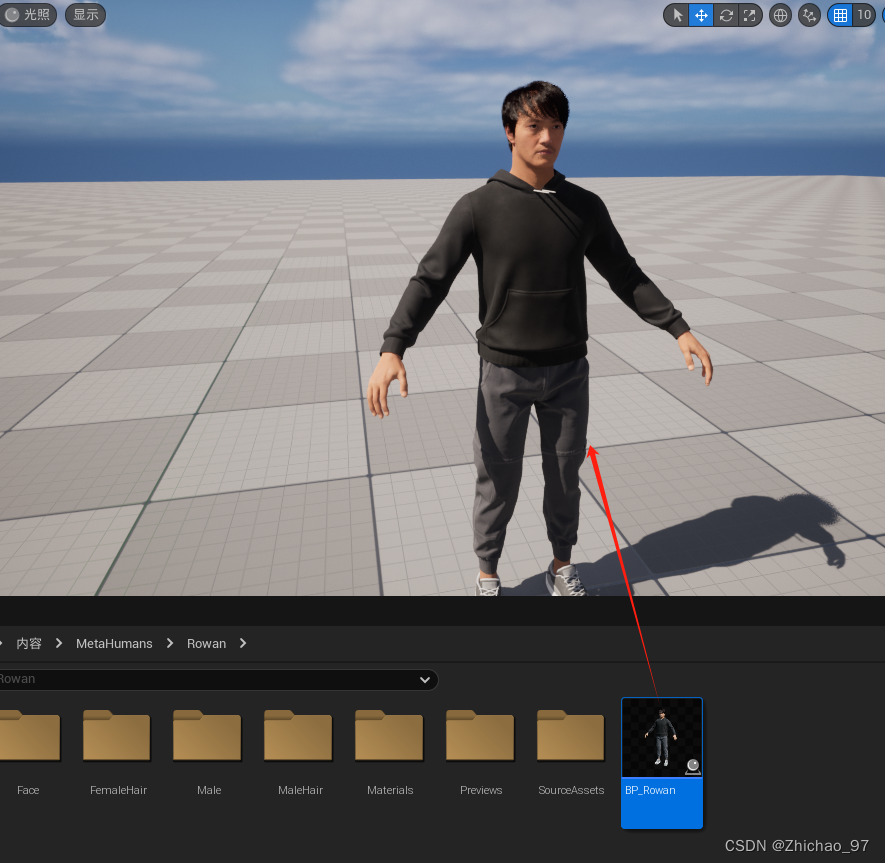
【UE5】初识MetaHuman 创建虚拟角色
步骤 在UE5工程中启用“Quixel Bridge”插件 打开“Quixel Bridge” 点击“MetaHumans-》MetaHuman Presets UE5” 点击“START MHC” 在弹出的网页中选择一个虚幻引擎版本,然后点击“启动 MetaHuman Creator” 等待一段时间后,在如下页面点击选择一个人…...

物流实时数仓:数仓搭建(DWD)一
系列文章目录 物流实时数仓:采集通道搭建 物流实时数仓:数仓搭建 物流实时数仓:数仓搭建(DIM) 物流实时数仓:数仓搭建(DWD)一 文章目录 系列文章目录前言一、文件编写1.目录创建2.b…...

MATLAB安装
亲自验证有效,多谢这位网友的分享: https://blog.csdn.net/xiajinbiaolove/article/details/88907232...
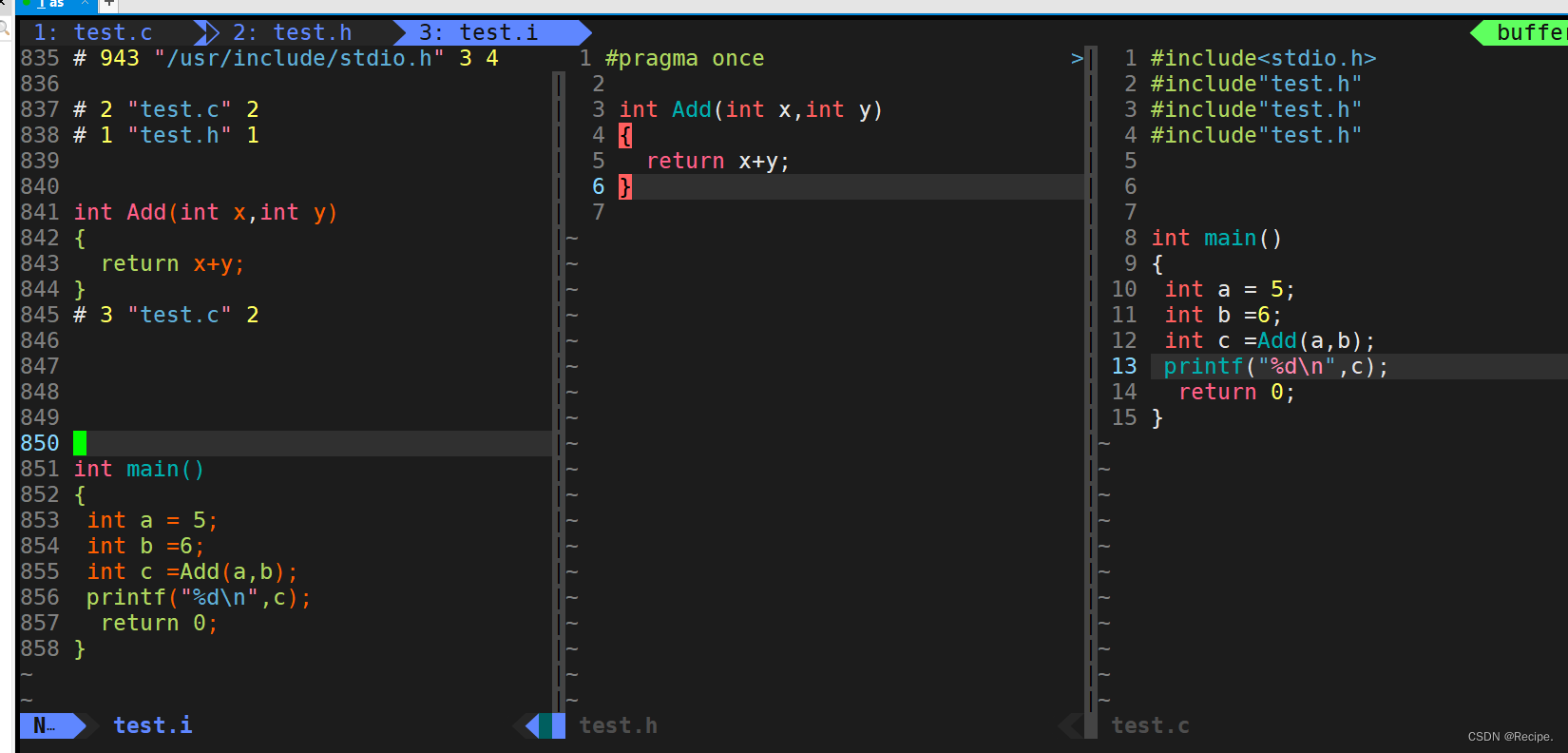
C语言——预处理详解(#define用法+注意事项)
#define 语法规定 #define定义标识符 语法: #define name stuff #define例子 #include<stdio.h> #define A 100 #define STR "abc" #define FOR for(;;)int main() {printf("%d\n", A);printf("%s\n", STR);FOR;return 0; } 运行结果…...

Linux(23):Linux 核心编译与管理
编译前的任务:认识核心与取得核心原始码 Linux 其实指的是核心。这个【核心(kernel)】是整个操作系统的最底层,他负责了整个硬件的驱动,以及提供各种系统所需的核心功能,包括防火墙机制、是否支持 LVM 或 Quota 等文件系统等等&a…...
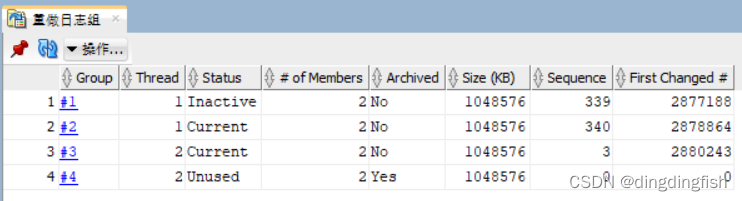
Oracle RAC环境下redo log 文件的扩容
环境: 有一个2节点RAC每一个节点2个logfile group每一个group含2个member每一个member的大小为200M 目标:将每一个member的大小有200M扩充到1G。 先来看下redo log的配置: SQL> select * from v$log;GROUP# THREAD# SEQUENCE# …...

Java入门学习笔记一
一、Java语言环境搭建 1、JAVA语言的跨平台原理 1.1、什么是跨平台性? 跨平台就是说,同一个软件可以在不同的操作系统(例如:Windows、Linux、mad)上执行,而不需要对软件做任务处理。即通过Java语言编写的…...

分布式块存储 ZBS 的自主研发之旅|元数据管理
重点内容 元数据管理十分重要,犹如整个存储系统的“大黄页”,如果元数据操作出现性能瓶颈,将严重影响存储系统的整体性能。如何提升元数据处理速度与高可用是元数据管理的挑战之一。SmartX 分布式存储 ZBS 采用 Log Replication 的机制&…...

六大设计原则
六大设计原则 1、单一职责原则 一个类或者模块只负责完成一个职责或者功能。 2、开放封闭原则 规定软件中的对象、类、模块和函数对扩展应该是开放的,对于修改应该是封闭的。用抽象定义结构,用具体实现扩展细节。 3、里氏替换原则 如果S是T的子类型…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...
