Leetcode 1901. 寻找峰值 II(Java + 列最大值 + 二分)
题目
- 1901. 寻找峰值 II
- 一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元
- 给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
- 你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
- 要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 500
- 1 <= mat[i][j] <= 10 ^ 5
- 任意两个相邻元素均不相等.
解法
Java + 列最大值 + 二分
第 1 步:
- 类似:Leetcode 162. 寻找峰值(Java + 二分)
- 在行内找严格大于左右的元素,再找每列的最大值(一定是大于上下)
- 一定需要找该列的最大值,如果这也二分找极大值(仅严格大于左右),那么可能找到非该列最大值从而导致 左/右 列误判
第 2 步:
- 具体做法:
- 先找中间=mid 列,找到俩最大值 mat[maxRow][mid] ,元素一定严格大于上下的元素
- 如果 mat[maxRow][mid] 严格大于左右的元素,则直接返回,否则下一步
- 如果 mat[maxRow][mid] > mat[maxRow][mid+1] 则 maxRow 左边列一定存在,否则 maxRow 右边列一定存在
- 时间复杂度:O(m*logn),空间复杂度:O(1)
代码
/*** Java + 列最大值 + 二分:** 第 1 步:* 类似:162. 寻找峰值 FindPeakElement,在行内找严格大于左右的元素,再找每列的最大值(一定是大于上下)* 一定需要找该列的最大值,如果这也二分找极大值(仅严格大于左右),那么可能找到非该列最大值从而导致 左/右 列误判** 第 2 步:* 具体做法:* * 先找中间=mid 列,找到俩最大值 mat[maxRow][mid] ,元素一定严格大于上下的元素* * 如果 mat[maxRow][mid] 严格大于左右的元素,则直接返回,否则下一步* * 如果 mat[maxRow][mid] > mat[maxRow][mid+1] 则 maxRow 左边列一定存在,否则 maxRow 右边列一定存在* 时间复杂度:O(m*logn),空间复杂度:O(1)***/public int[] findPeakGrid(int[][] mat) {int leftCol = 0;int rightCol = mat[0].length - 1;int resCol = 0;while (leftCol <= rightCol) {int midCol = ((rightCol - leftCol) >> 1) + leftCol;int maxRow = getMaxRow(mat, midCol);if ((midCol == 0 || mat[maxRow][midCol] > mat[maxRow][midCol - 1])&& (midCol == mat[0].length - 1 || mat[maxRow][midCol] > mat[maxRow][midCol + 1])) {resCol = midCol;break;}if (midCol == mat[0].length - 1 || mat[maxRow][midCol] > mat[maxRow][midCol + 1]) {rightCol = midCol - 1;} else {leftCol = midCol + 1;}}return new int[]{getMaxRow(mat, resCol), resCol};}private int getMaxRow(int[][] mat, int resCol) {int maxRow = 0;for (int i = 0; i < mat.length; i++) {if (mat[maxRow][resCol] < mat[i][resCol]) {maxRow = i;}}return maxRow;}
相关文章:
)
Leetcode 1901. 寻找峰值 II(Java + 列最大值 + 二分)
题目 1901. 寻找峰值 II 一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。你可以假设整个矩阵周边…...

RabbitMQ 消息持久化
默认情况下,exchange、queue、message 等数据都是存储在内存中的,这意味着如果 RabbitMQ 重启、关闭、宕机时所有的信息都将丢失。 RabbitMQ 提供了持久化来解决这个问题,持久化后,如果 RabbitMQ 发送 重启、关闭、宕机ÿ…...

Opencv实验合集——实验四:图片融合
1.概念 图像融合是将两个或多个图像结合在一起,创建一个新的图像的过程。这个过程的目标通常是通过合并图像的信息来获得比单个图像更全面、更有信息量的结果。图像融合可以在许多领域中应用,包括计算机视觉、遥感、医学图像处理等。 融合的方法有很多…...

Java复习
CH1 Java Fundamentals 1.1 Java Features(java特色) 1.1 Simplicity: simple grammar, rich library 简单好用: 语法简单,库文件丰富 1.2 Pure OO: everything is object! 所有程序都是对象 1.3 Security: memory access,…...
腾讯云微服务11月产品月报 | TSE 云原生 API 网关支持 WAF 对象接入
2023年 11月动态 TSE 云原生 API 网关 1、支持使用私有 DNS 解析 服务来源支持私有 DNS 解析器,用户可以添加自己的 DNS 解析器地址进行私有域名解析,适用于服务配置了私有域名的用户。 2、支持 WAF 对象接入 云原生 API 网关对接 Web 安全防火墙&…...

性能优化-待处理
1 性能优化-循环展开...

Linux: sysctl: network: ip_no_pmtu_disc,容易搞混的参数名称
这个参数的迷惑性在于双重否定,字面意思是关闭PMTU发现的功能。如果设置为1,代表关闭;如果是0,代表不关闭pmtu发现的功能。所以说明里,有disable/enable,就容易搞混。所以要甄别网上的某些博客的说明,不要被误导。 ip_no_pmtu_disc - INTEGER Disable Path MTU Discover…...

关于“Python”的核心知识点整理大全26
目录 10.3.9 决定报告哪些错误 10.4 存储数据 10.4.1 使用 json.dump()和 json.load() number_writer.py number_reader.py 10.4.2 保存和读取用户生成的数据 对于用户生成的数据,使用json保存它们大有裨益,因为如果不以某种方式进行存储…...

Axure中继器完成表格的增删改查的自定义元件(三列表格与十列表格)
目录 一、中继器 1.1 定义 1.2 特点 1.3 适用场景 二、三列表格增删改查 2.1 实现思路 2.2 效果演示 三、十列表格增删改查 3.1 实现思路 3.2 效果演示 一、中继器 1.1 定义 在Axure中,"中继器"通常指的是界面设计中的一个元素,用…...

刚clone下来的项目如何上传到新的仓库
查看当前项目的git信息 git remote -v 查看git目录上传到哪个路径下 拉下的项目如何上传到新的仓库 git clone xxxcd xxxrm -r .git 删除原有的git信息,有问题一直回车git init 初始化gitgit add . git commit -m ‘xxx’git remote add origin 远程库地址&#…...
【ARMstm32】【华清远见西安中心】)
面试题总结(十五)【ARMstm32】【华清远见西安中心】
ARM Cortex-M,Cortex-R,Cortex-A的区别和差异是什么? ARM Cortex-M,Cortex-R和Cortex-A是ARM架构下的不同处理器系列,针对不同的应用领域和需求进行了优化和设计。它们之间的区别和差异主要体现在以下几个方面: 1. 应用领域&#…...
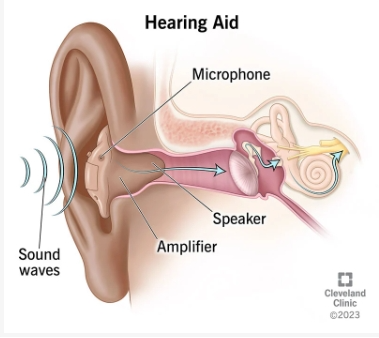
助听器概述
助听器概述 什么是助听器? 助听器是一种放置在耳内或耳后的小型电子设备。助听器可以放大声音,使听力损失的人能够提高他们的听力和言语理解能力。 今天有许多不同类型的助听器,包括处方助听器和非处方 (OTC) 助听器…...
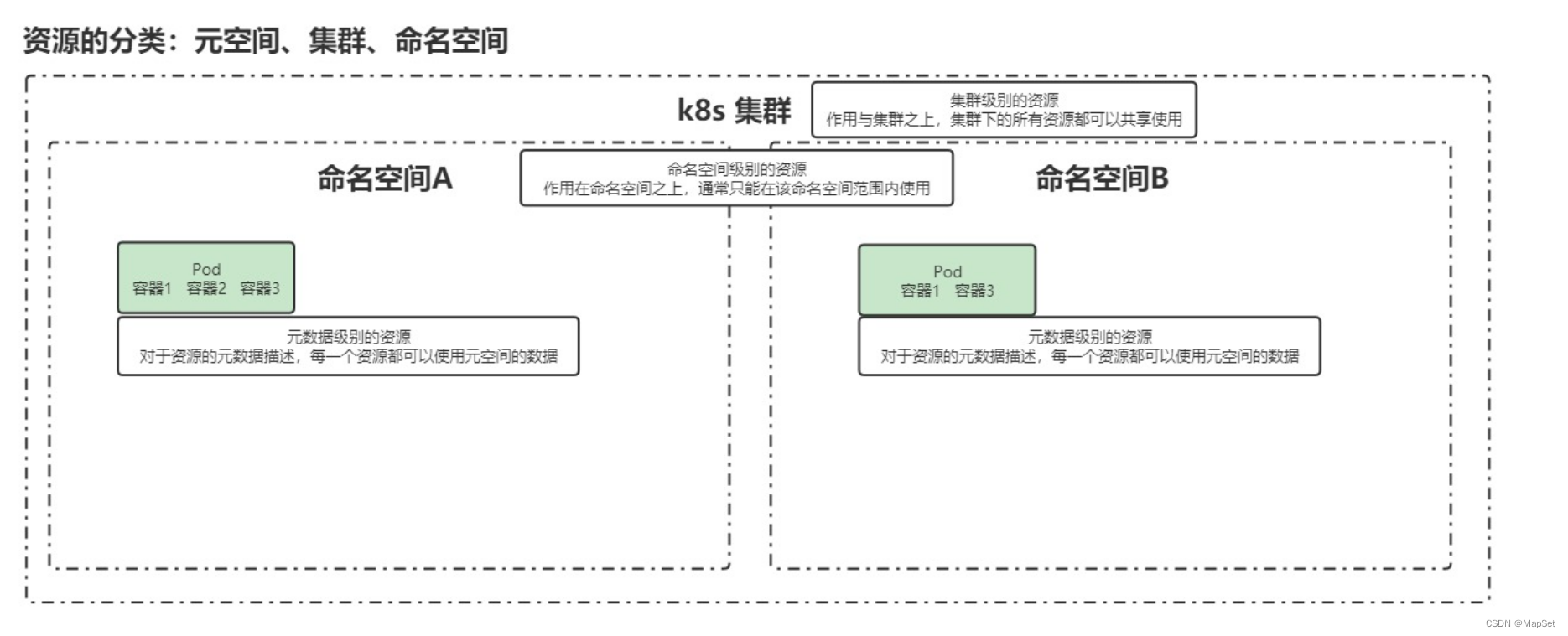
学习k8s
学习k8s 我为什么要用k8s 和其他部署方式的区别是什么? 传统部署方式 java --> package --> 放到服务器上 --> Tomcat 如果是同时进行写操作,会存在并发问题. 用户 --网络带宽–> 服务器 -->服务 同一个服务器上,多个服务: 网络资源的占用 内存的占用 cpu的占…...

iOS 将sdk更新到最新并为未添加版本号的三方库增加版本号
1、更新cocoapod sudo gem install cocoapods2、更新sdk pod update3、查看最新版本号 # 查看最新版本号 cat Podfile.lock4、增加版本号 将查询到的版本号添加到pod中 pod MJRefresh, 3.7.6...
Appium —— 初识移动APP自动化测试框架Appium
说到移动APP自动化测试,代表性的测试框架非Appium莫属,从今天开始我们将从APP结构解析、Appium框架学习、安卓/iOS自动化测试实战、自动遍历回归测试、自动化测试平台及持续集成,多个维度一起由浅入深的学废Appium 今天我们先来初步认识Appi…...

自助式可视化开发,ETLCloud的集成之路
自助式可视化开发 自助式可视化开发是指利用可视化工具和平台,使非技术人员能够自主创建、定制和部署数据分析和应用程序的过程。 传统上,数据分析和应用程序开发需要专业的编程和开发技能。但是,自助式可视化开发工具的出现,使…...
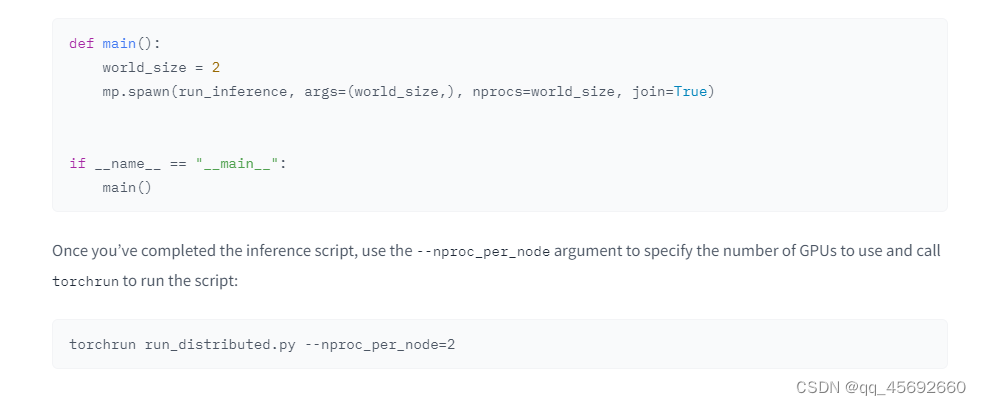
diffu-Distributed inference with multiple GPUs
pytorch的ddp...

在Python中使用Kafka帮助我们处理数据
Kafka是一个分布式的流数据平台,它可以快速地处理大量的实时数据。Python是一种广泛使用的编程语言,它具有易学易用、高效、灵活等特点。在Python中使用Kafka可以帮助我们更好地处理大量的数据。本文将介绍如何在Python中使用Kafka简单案例。 一、安装K…...

进程和线程和协程区别
目录 一、进程和线程 二、线程上下文切换 三、线程与协程区别 一、进程和线程 线程是可以由调度程序对立管理的最小程序指令集,而进程是程序运行的实例。 大多情况下,线程是进程的组成部分,一个进程中可以存在多个线程,这些线…...
银行测试:第三方支付平台业务流,功能/性能/安全测试方法
1、第三方支付平台的功能和结构特点 在信用方面,第三方支付平台作为中介,在网上交易的商家和消费者之间作一个信用的中转,通过改造支付流程来约束双方的行为,从而在一定程度上缓解彼此对双方信用的猜疑,增加对网上购物…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
