数据结构:图解手撕B-树以及B树的优化和索引
文章目录
- 为什么需要引入B-树?
- B树是什么?
- B树的插入分析
- B+树和B*树
- B+树
- B*树
- 分裂原理
- B树的应用
本篇总结的内容是B-树
为什么需要引入B-树?
回忆一下前面的搜索结构,有哈希,红黑树,二分…等很多的搜索结构,而实际上这样的结构对于数据量不是很大的情况是比较适用的,但是假设有一组很大的数据,大到已经不能在内存中存储,此时应该如何处理呢?可以考虑将关键字及其映射的数据的地址放到一个内存中的搜索树的节点,优先考虑去这个地址处访问数据
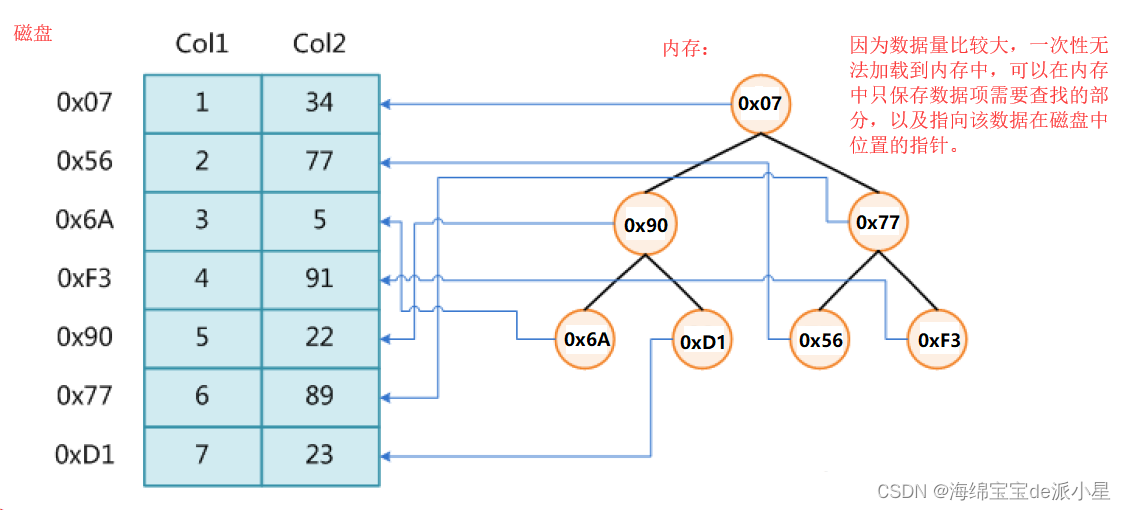

从上面的文段中可以看出,问题出现在文件的IO是有损耗的,因此在使用哈希或是其他的数据结构,在搜索的过程中会不断地进行文件的IO,这样带来的降低效率是不建议出现的,因此解决方案之一就是可以降低树的高度,因此就引出了B-树:多叉平衡树
B树是什么?
1970年,R.Bayer和E.mccreight提出了一种适合外查找的树,它是一种平衡的多叉树,称为B树(后面有一个B的改进版本B+树,然后有些地方的B树写的的是B-树,一棵m阶(m>2)的B树,是一棵平衡的M路平衡搜索树,可以是空树或者满足一下性质:
- 根节点至少有两个孩子
- 每个分支节点都包含
k-1个关键字和k个孩子,其中ceil(m/2) ≤ k ≤ m ceil是向上取整函数 - 每个叶子节点都包含
k-1个关键字,其中ceil(m/2) ≤ k ≤ m - 所有的叶子节点都在同一层
- 每个节点中的关键字从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域划分
- 每个结点的结构为:
(n,A0,K1,A1,K2,A2,… ,Kn,An)其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1,n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1
上面的规则很复杂,那么下面用图片来解释B树的插入原理,并进行一次模拟
B树的插入分析
假设此时的M = 3,也就是这是一个三叉树,那么从上面的规则来说,每个节点要存储两个数据,还有三个孩子节点,而实际上的过程中会分别多创建一个节点,也就是说会创建三个数据域和四个孩子节点,这样的好处后续在实现代码的过程中会体现出来
假设现在给定了这样的一组数据:53, 139, 75, 49, 145, 36, 101
图解如下:
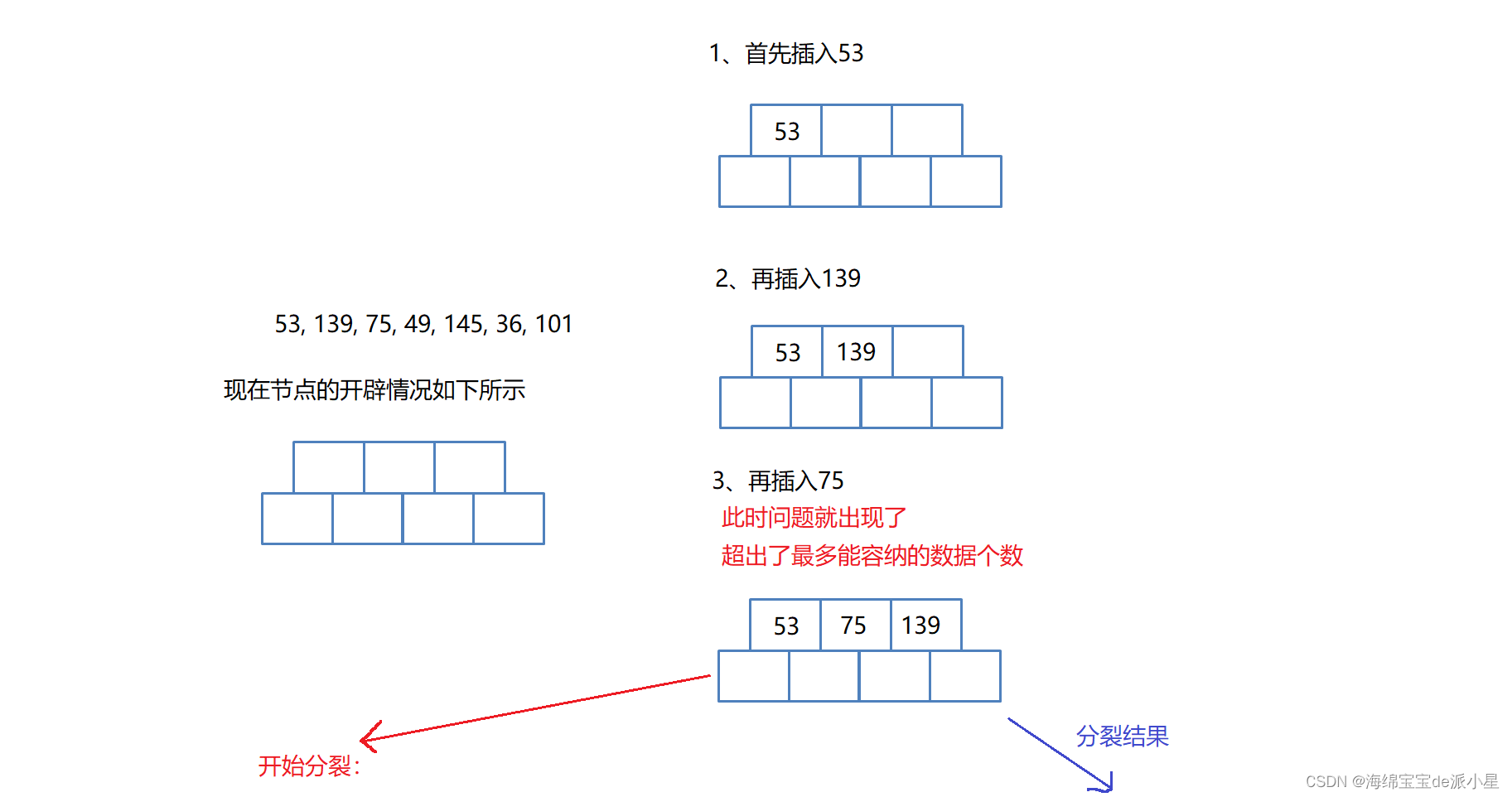
那么超过了可以容纳的数据个数,该如何处理呢?看B树的规则是如何处理的:
B树的分裂规则:
当超过了最多能容纳的数据个数后,会进行分裂:
- 找到节点数据域的中间位置
- 创建一个兄弟节点,把后一半的数据挪动到兄弟节点中
- 把中位数的数据移动到父节点中
- 对这些节点建立链接
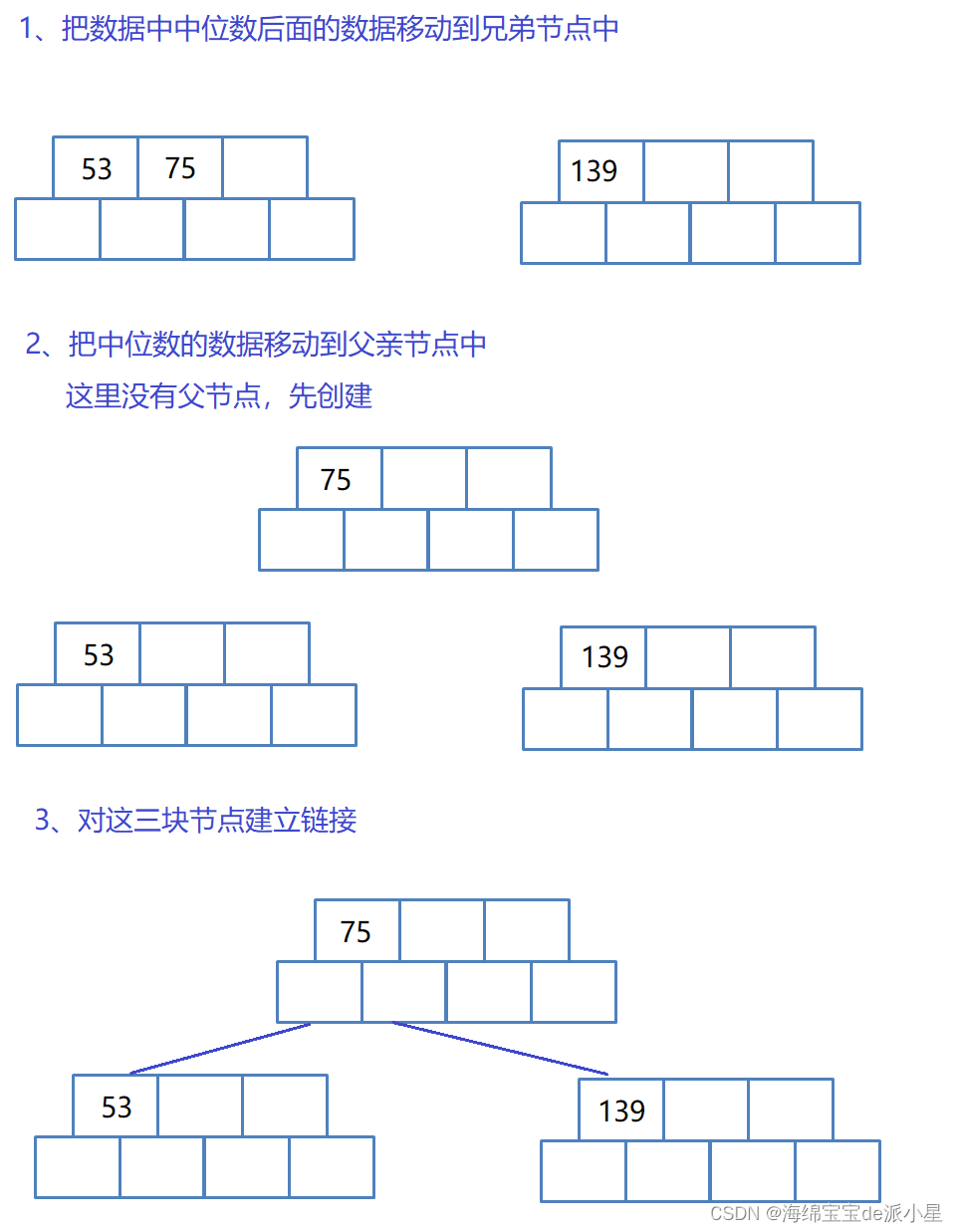
此时就完成了B树的一次分裂,从中就能看出B树的基本原理,既然是多叉搜索树,那么也要满足搜索树的规则,因此采取这样的分裂规则是可以满足搜索树的要求的
继续进行插入数据,按照上述的原理即可

当继续插入的时候,就会产生新的分裂问题:
由此得出了最终的生成图
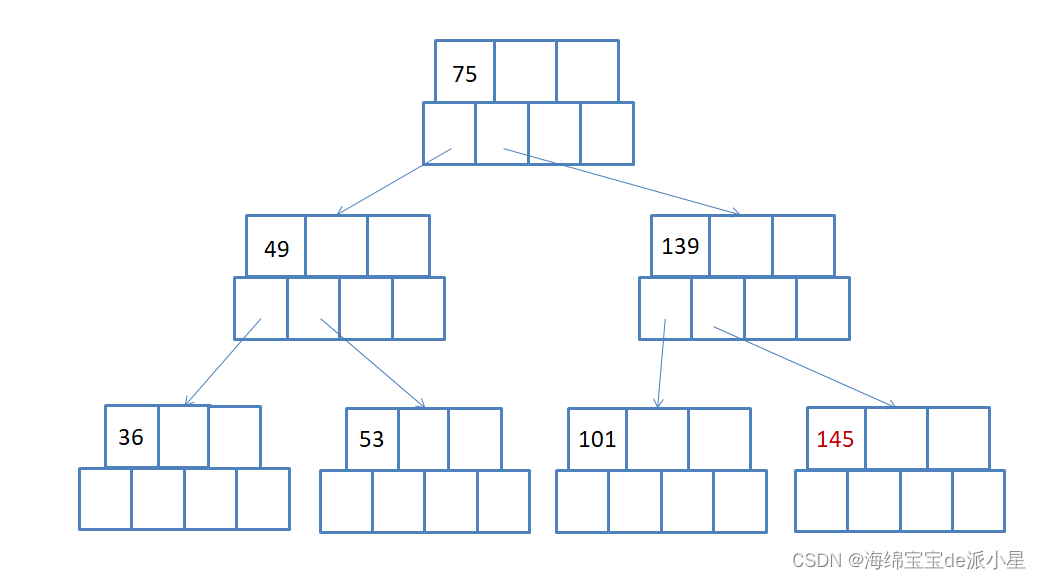
从这个图中也能看出,确实是符合搜索树的预期的,那么下一步就是要把上面写的这一系列的过程转换成代码来进行实现
#include <iostream>
using namespace std;// 定义B树节点的信息
template <class K, size_t M>
struct BTreeNode
{// 节点内部包含一个数组用来存储数据域信息,和一个指针数组用来保存孩子节点信息,以及双亲的信息// 还要包括节点中已经存储的数据的数量// 多开辟一个空间,方便于判断是否需要进行分裂K _keys[M];BTreeNode<K, M>* _subs[M + 1];BTreeNode<K, M>* _parent;size_t _n;BTreeNode():_parent(nullptr), _n(0){for (int i = 0; i < M; i++){_subs[i] = nullptr;_keys[i] = nullptr;}_subs[M] = nullptr;}
};// 存储B树的信息
template <class K, size_t M>
class BTree
{typedef BTreeNode<K, M> Node;
public:// 查找函数,找某个确定的Key值,如果找到了返回它所在的节点和所处节点的位置pair<Node*, int> Find(const K& key){Node* parent = nullptr;Node* cur = _root;// 开始寻找while (cur){size_t i = 0;// 指针到每一层的节点后进行比较while (i < cur->_n){if (key < cur->_keys){// 说明此时要查找的节点信息不在这一层,一定是要到下面一层去找,因此跳出这一层的循环break;}else if (key > cur->_keys){// 说明此时要查找的信息可能在当前查找的节点的后面,还要去后面找找看i++;}else{// 说明此时找到节点的信息了,直接把节点的信息进行返回即可return make_pair(cur, i);}}// 说明此时这一层已经找完了,现在该去下一层进行寻找了parent = cur;// 由B树的性质得出,subs[i]中存储的信息是比当前信息要小的树,因此去这里寻找目标Key值cur = cur->_subs[i];}// 运行到这里就是这个值在B树中不存在,返回查找最后的层数的节点和错误值即可return make_pair(parent, -1);}// 把元素插入到表中,本质上是一种插入排序void InsertKey(Node* node, const K& key, Node* child){int end = node->_n - 1;while (end >= 0){if (key < node->_keys[end]){// 挪动key和他的右孩子node->_keys[end + 1] = node->_keys[end];node->_subs[end + 2] = node->_subs[end + 1];--end;}else{break;}}// 把值写入到节点中node->_keys[end + 1] = key;node->_subs[end + 2] = child;// 如果有孩子节点,那么要更新孩子节点的指向,插入元素后双亲所在的位置发生了变化if (child)child->_parent = node;node->_n++;}bool Insert(const K& key){// 如果_root是一个空树,那么直接创建节点再把值放进去即可if (_root == nullptr){_root = new Node;_root->_keys[0] = key;_root->_n++;return true;}// 运行到这里,说明这个树不是一个空树,那么首先要寻找插入的节点在现有的B树中是否存在pair<Node*, int> ret = Find(key);if (ret.second != -1){// 键值对的第二个信息不是-1,说明在B树中找到了要插入的信息,这是不被允许的,因此返回return false;}// 运行到这里,说明要开始向B树中插入新节点了// 并且前面的ret还找到了parent,也就是实际应该是插入的位置信息Node* parent = ret.first;K newKey = key;// 创建孩子指针的意义是,后续可能会重复的进行分裂情况,并且插入元素的节点中可能原先有值// 直接插入后,会把原来孩子节点的双亲节点发生替换,因此要改变孩子节点的指向Node* child = nullptr;while (1){// 此时就找到了要插入的元素,要插入的位置,进行插入InsertKey(parent, newKey, child);// 如果双亲节点没有超出限制,那么就说明此时插入已经完成了if (parent->_n < M){return true;}else{// 运行到这里时,就说明已经超过了节点能容纳的最大值,此时应该进行分裂处理// 找到中间的元素size_t mid = M / 2;// 把[mid + 1, M - 1]分配个兄弟节点Node* brother = new Node;size_t j = 0;size_t i = mid + 1;for (; i <= M - 1; ++i){// 分裂拷贝key和key的左孩子,把这些信息拷贝给兄弟节点brother->_keys[j] = parent->_keys[i];brother->_subs[j] = parent->_subs[i];if (parent->_subs[i])parent->_subs[i]->_parent = brother;++j;// 被拷贝走的元素所在的位置进行重置,表明已经被拷贝走了parent->_keys[i] = K();parent->_subs[i] = nullptr;}// 还有最后一个右孩子拷给brother->_subs[j] = parent->_subs[i];if (parent->_subs[i])parent->_subs[i]->_parent = brother;parent->_subs[i] = nullptr;// 更新一下原先节点和兄弟节点中的元素的个数brother->_n = j;parent->_n -= (brother->_n + 1);K midKey = parent->_keys[mid];parent->_keys[mid] = K();// 说明刚刚分裂是根节点,要创建一个新的根节点用来存储分裂的中位数的信息if (parent->_parent == nullptr){_root = new Node;_root->_keys[0] = midKey;_root->_subs[0] = parent;_root->_subs[1] = brother;_root->_n = 1;parent->_parent = _root;brother->_parent = _root;break;}else{// 向parent中插入一个中位数,同时更新一下孩子的信息即可// 转换成往parent->parent 去插入parent->[mid] 和 brothernewKey = midKey;child = brother;parent = parent->_parent;}}}return true;}
private:Node* _root = nullptr;
};
B+树和B*树
B+树
B+树是B树的变形,是在B树基础上优化的多路平衡搜索树,B+树的规则跟B树基本类似,但是又在B树的基础上做了以下几点改进优化:
- 分支节点的子树指针与关键字个数相同
- 分支节点的子树指针p[i]指向关键字值大小在[k[i],k[i+1])区间之间
- 所有叶子节点增加一个链接指针链接在一起
- 所有关键字及其映射数据都在叶子节点出现
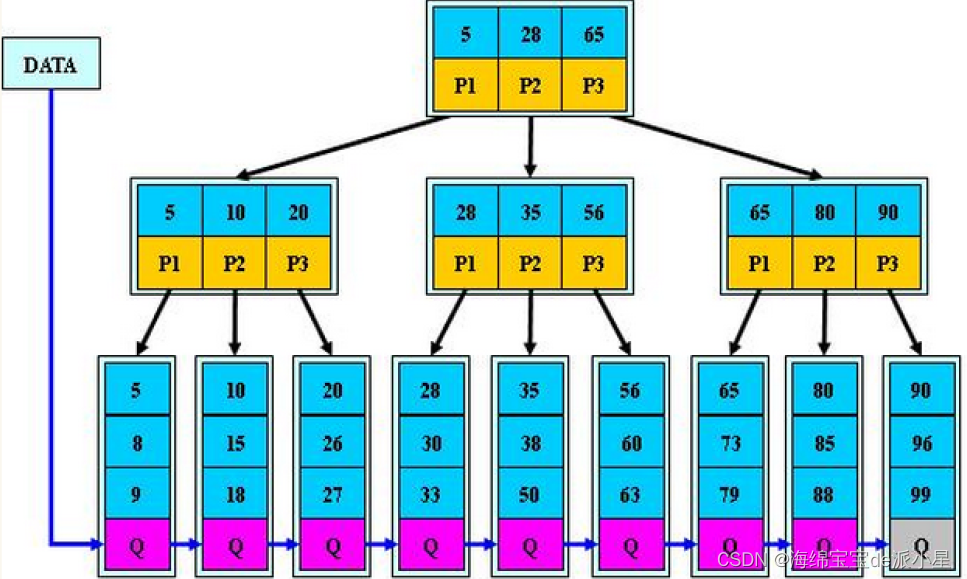
B+树的特性:
- 所有关键字都出现在叶子节点的链表中,且链表中的节点都是有序的
- 不可能在分支节点中命中
- 分支节点相当于是叶子节点的索引,叶子节点才是存储数据的数据层
B*树
B*树是B+树的变形,在B+树的非根和非叶子节点再增加指向兄弟节点的指针
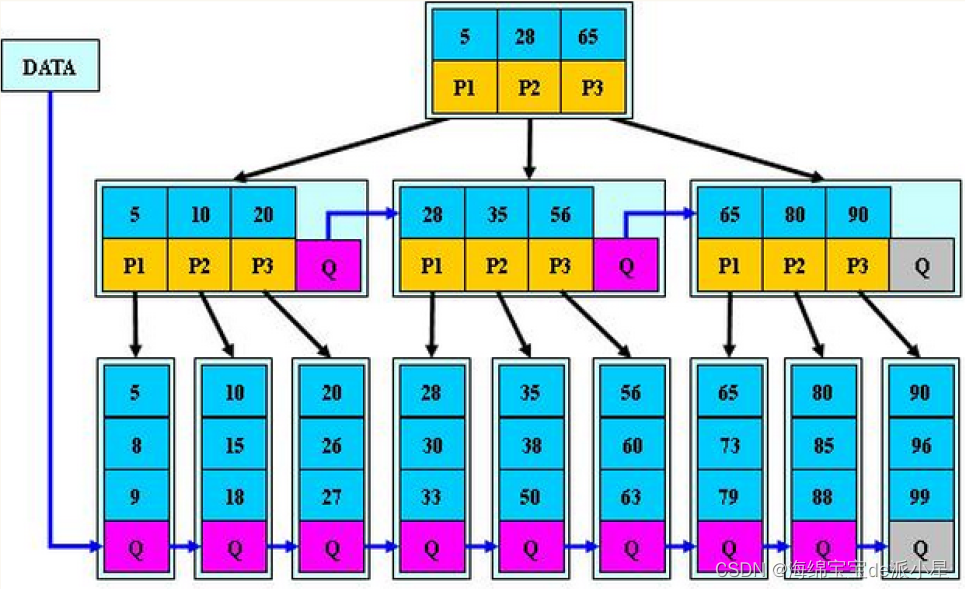
分裂原理
B+树的分裂:
当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针
B*树的分裂:
当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针
所以,B*树分配新结点的概率比B+树要低,空间使用率更高
B树:有序数组+平衡多叉树
B+树:有序数组链表+平衡多叉树
B*树:一棵更丰满的,空间利用率更高的B+树
B树的应用
B树的最常见应用就是当做索引
MySQL官方对索引的定义为:索引(index)是帮助MySQL高效获取数据的数据结构,简单来说:索引就是数据结构
当数据量很大时,为了能够方便管理数据,提高数据查询的效率,一般都会选择将数据保存到数据库,因此数据库不仅仅是帮助用户管理数据,而且数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用数据,这样就可以在这些数据结构上实现高级查找算法,该数据结构就是索引
mysql是目前非常流行的开源关系型数据库,不仅是免费的,可靠性高,速度也比较快,而且拥
有灵活的插件式存储引擎
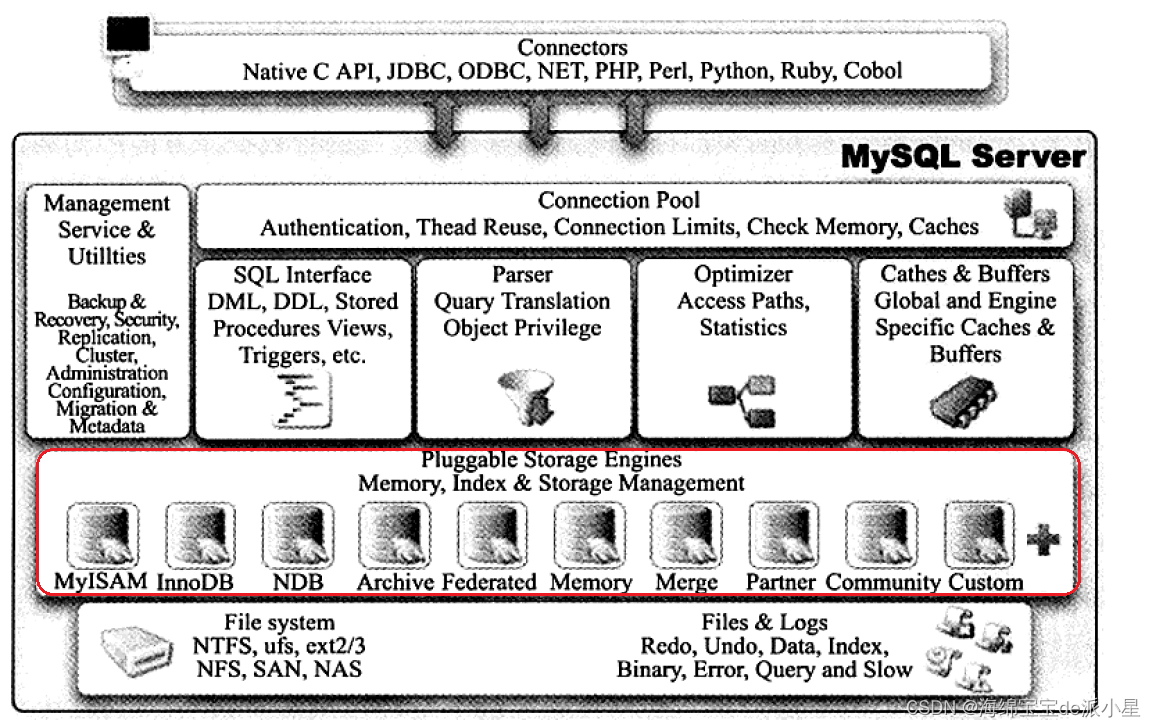
相关文章:

数据结构:图解手撕B-树以及B树的优化和索引
文章目录 为什么需要引入B-树?B树是什么?B树的插入分析B树和B*树B树B*树分裂原理 B树的应用 本篇总结的内容是B-树 为什么需要引入B-树? 回忆一下前面的搜索结构,有哈希,红黑树,二分…等很多的搜索结构&a…...
useConsole的封装,vue,react,htmlscript标签,通用
之前用了接近hack的方式实现了console的封装,目标是获取console.log函数的执行(调用栈所在位置)所在的代码行数。 例如以下代码,执行window.mylog(1)时候,console.log实际是在匿名的箭头函数()>{//这里执行的} con…...

Azure Machine Learning - 提示工程高级技术
本指南将指导你提示设计和提示工程方面的一些高级技术。 关注TechLead,分享AI全维度知识。作者拥有10年互联网服务架构、AI产品研发经验、团队管理经验,同济本复旦硕,复旦机器人智能实验室成员,阿里云认证的资深架构师,…...

七款创意项目管理软件解决方案推荐:高效项目管理与团队协作工具
企业无论大小,都离不开项目经理、营销团队和创意人员。他们参与各种头脑风暴,为特定目标打造项目。然而,在创意项目管理中,细节决定成败。若处理不当,可能导致项目失败和混乱。 过去,创意项目管理依赖纸质规…...
如何在公网环境下使用Potplayer访问本地群晖webdav中的影视资源
文章目录 本教程解决的问题是:按照本教程方法操作后,达到的效果是:1 使用环境要求:2 配置webdav3 测试局域网使用potplayer访问webdav3 内网穿透,映射至公网4 使用固定地址在potplayer访问webdav 国内流媒体平台的内…...

数据可视化Seaborn
数据可视化Seaborn Seaborn简介Seaborn API第一个Seaborn应用Seaborn基本概念Seaborn图表类型Seaborn数据集Seaborn样式Seaborn调色板Seaborn分面网格Seaborn统计图表Seaborn散点图Seaborn折线图Seaborn柱状图Seaborn箱线图Seaborn核密度估计图Seaborn分类散点图Seaborn回归分…...

AWS S3相关配置笔记
关闭 阻止所有公开访问 存储桶策略(开放外部访问) {"Version": "2012-10-17","Id": "S3PolicyId1","Statement": [{"Sid": "statement1","Effect": "Allow","Principal"…...

linux:linux的小动物们(ubuntu)
1.蒸汽小火车 输入下面的命令下载,再输出sl sudo apt-get install sl sl2.今天你哞了吗 apt-get moo 3.会说话的小牛 输入下面的命令下载一下 sudo apt-get install cowsay输入这个 cowsay jianbing cowsay -l 查看其它动物的名字 然后cowsay -f 跟上动物名&…...
----栈和队列--逆波兰表达式求值)
每日一题(LeetCode)----栈和队列--逆波兰表达式求值
每日一题(LeetCode)----栈和队列–逆波兰表达式求值 1.题目(150. 逆波兰表达式求值) 给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。 请你计算该表达式。返回一个表示表达式值的整数。 注意: 有效的算…...
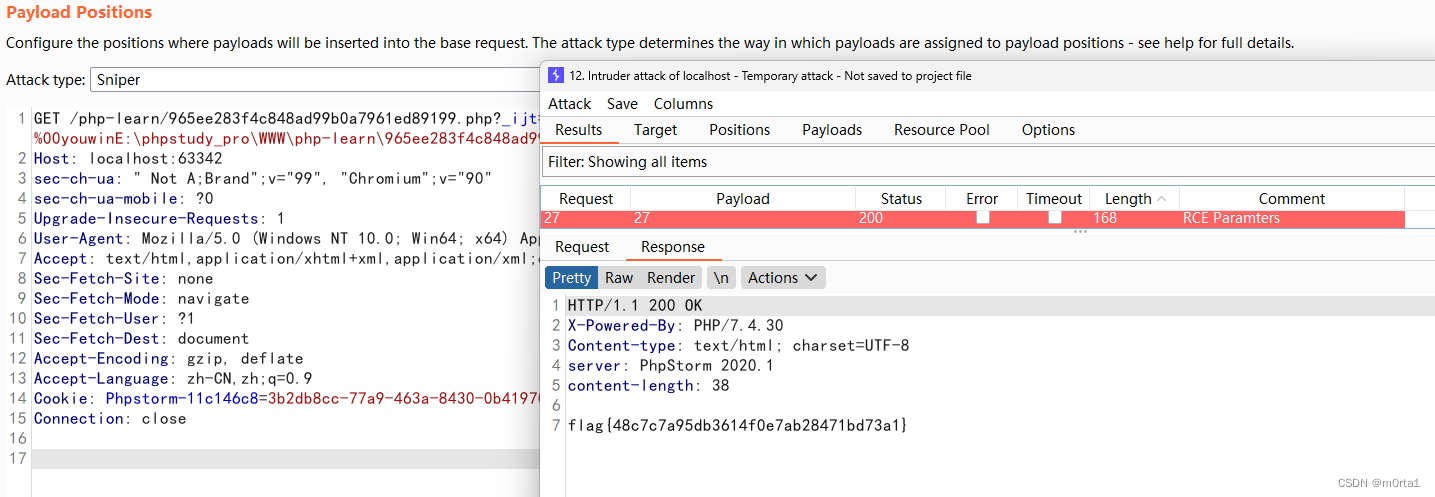
2023年第四届 “赣网杯” 网络安全大赛 gwb-web3 Write UP【PHP 临时函数名特性 + 绕过trim函数】
一、题目如下: 二、代码解读: 这段代码是一个简单的PHP脚本,它接受通过GET请求传递的两个参数:‘pass’和’func’: ① $password trim($_GET[pass] ?? );:从GET请求中获取名为’pass’的参数࿰…...
软件设计师——软件工程(一)
📑前言 本文主要是【软件工程】——软件设计师——软件工程的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 🌄…...

阿里云|人工智能(AI)技术解决方案
函数计算部署Stable Diffusion AI绘画技术解决方案 通过函数计算快速部署Stable Diffusion模型为用户提供快速通过文字生成图片的能力。该方案通过函数计算快速搭建了AIGC的能力,无需管理服务器等基础设施,专注模型的能力即可。该方案具有高效免运维、弹…...
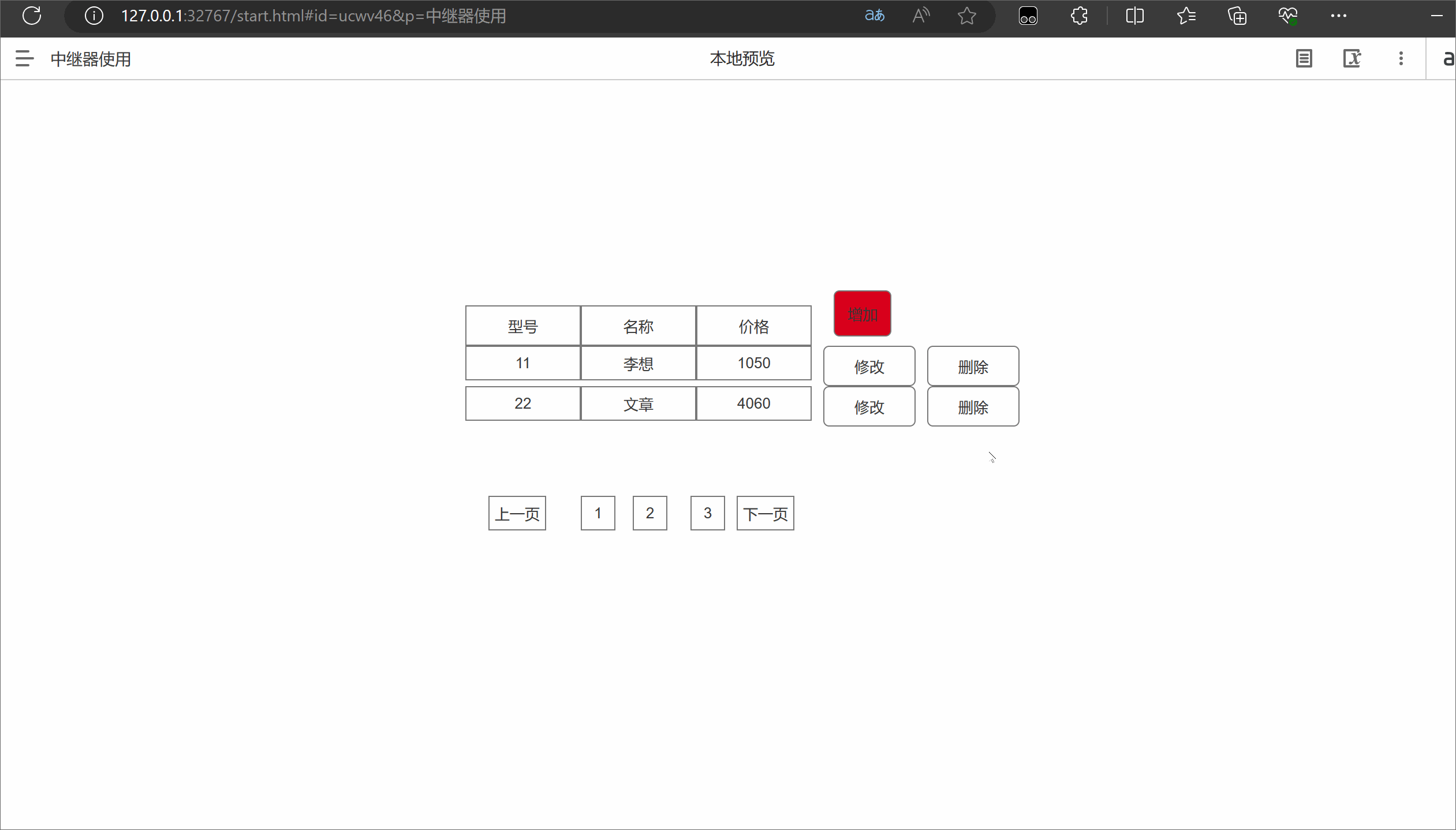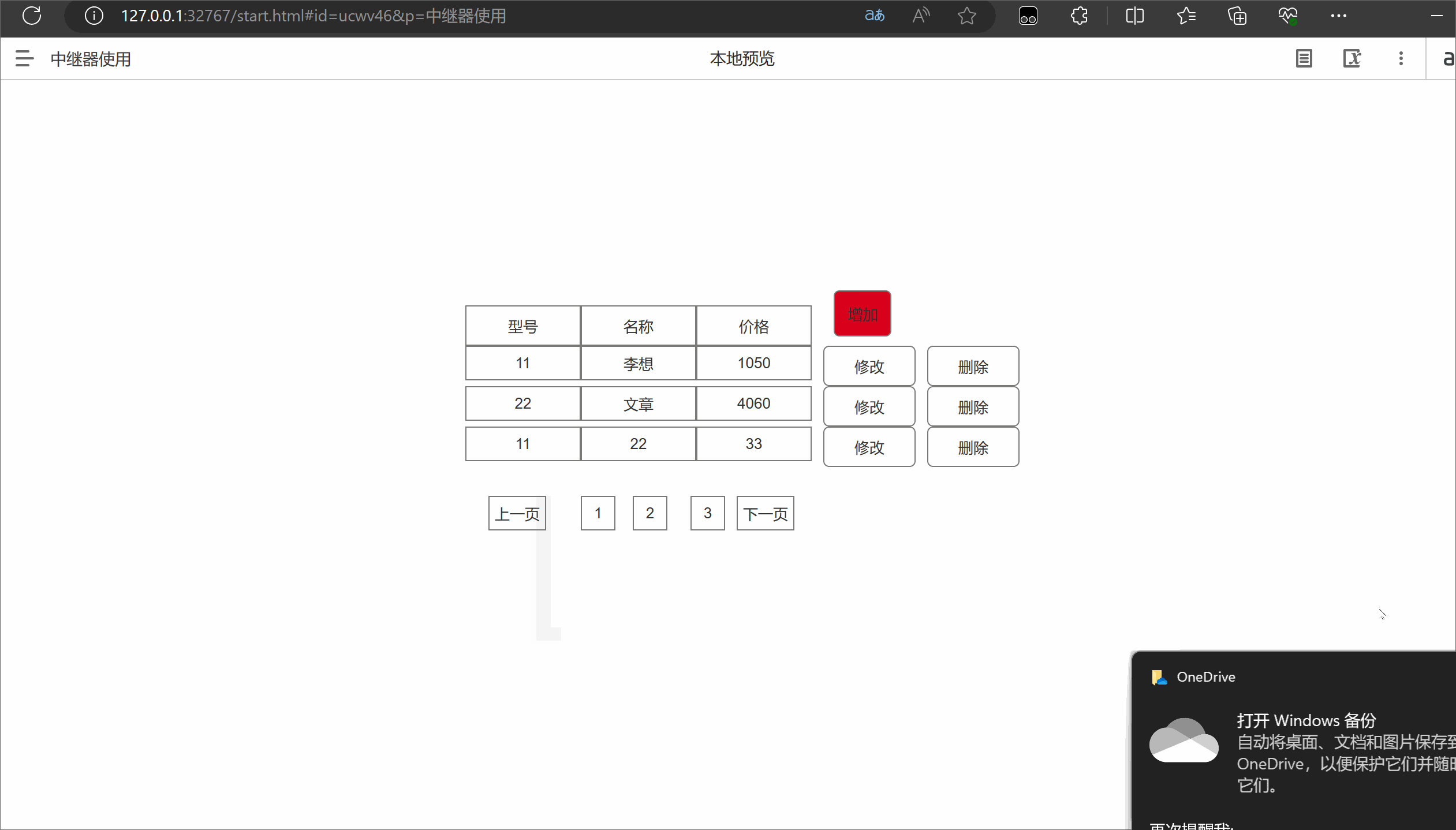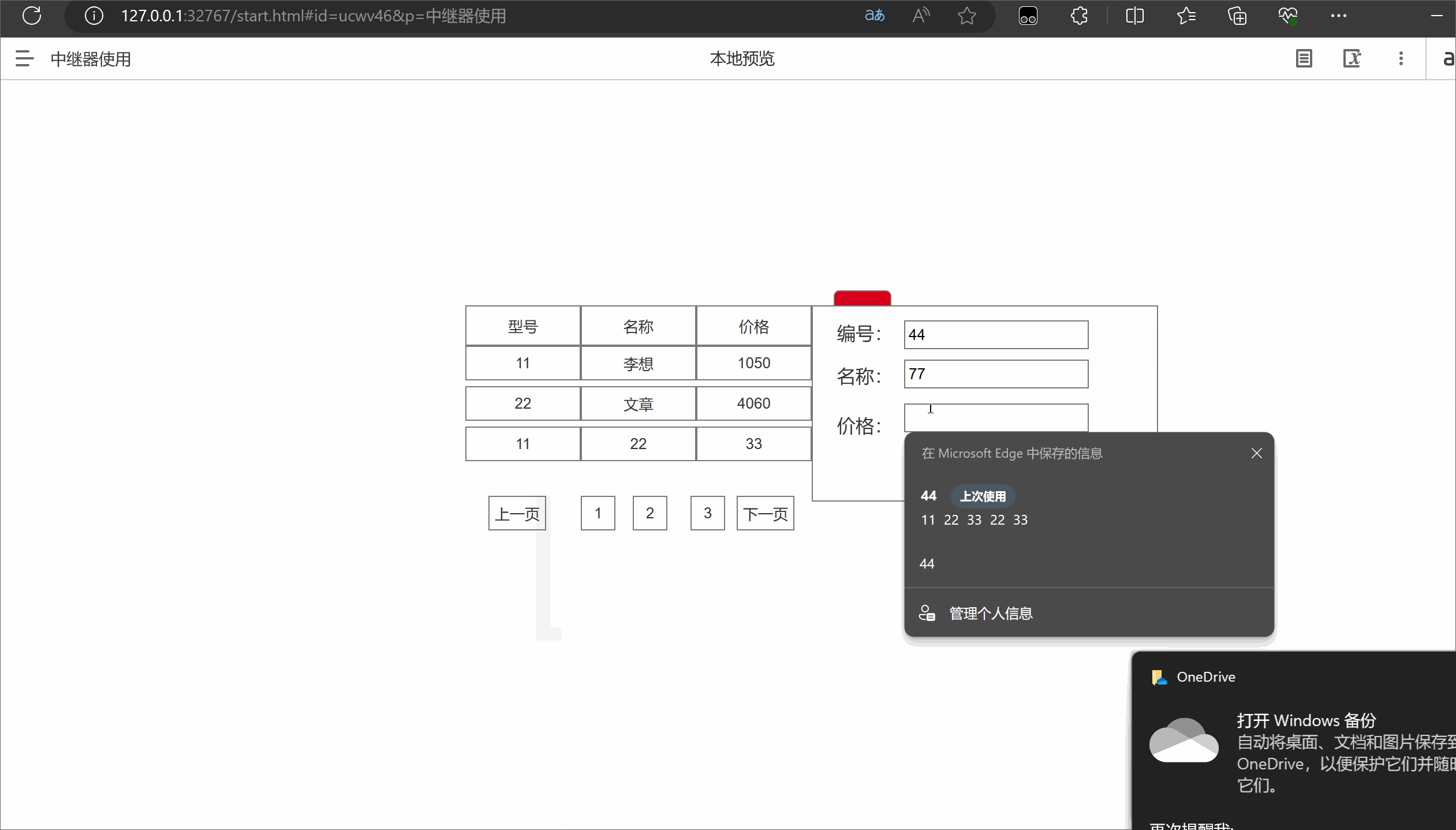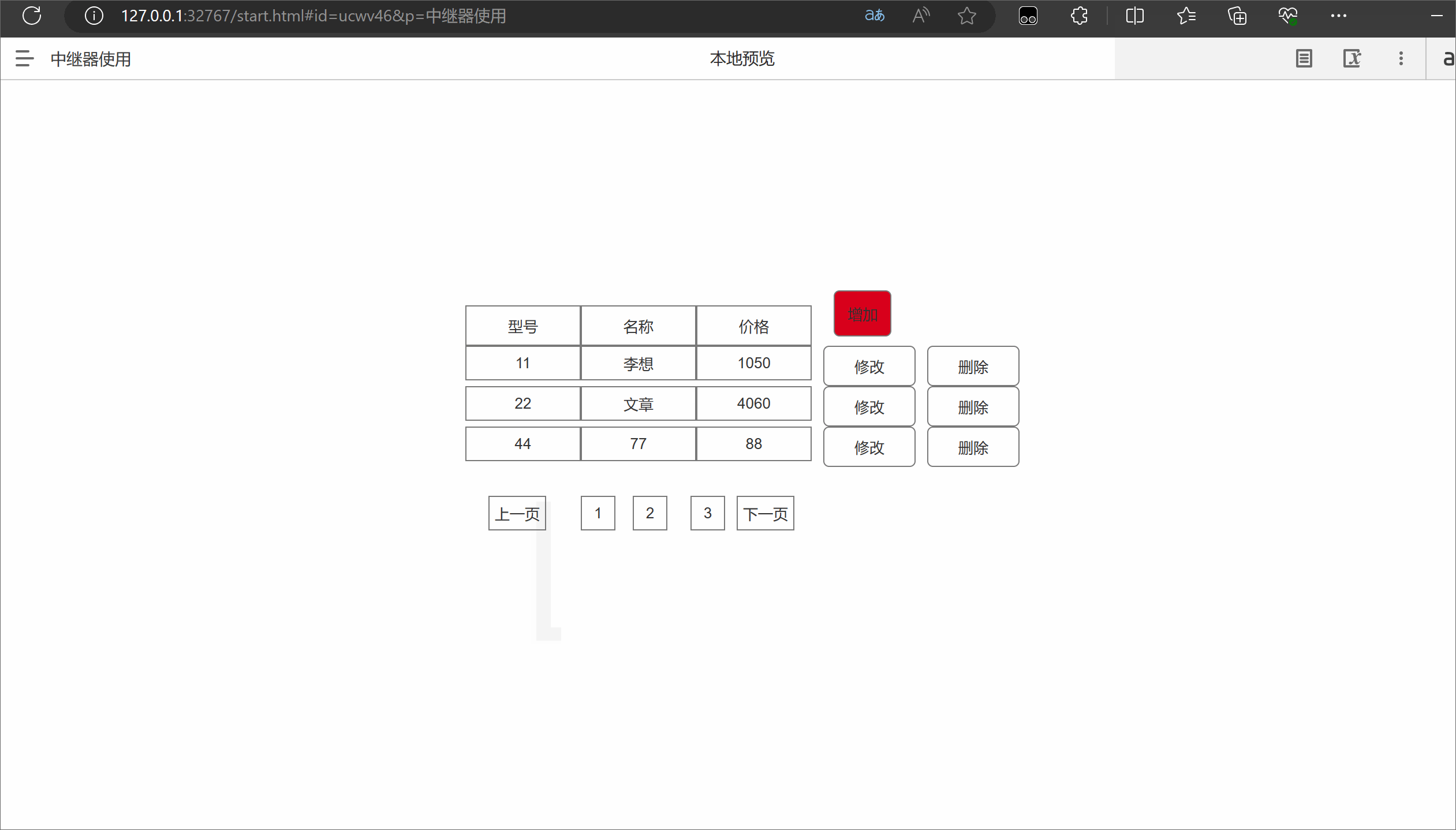
Axure中继器的使用
一.中继器介绍 在Axure中,中继器(Relays)是一种功能强大的元件,可以用于创建可重复使用的模板或组件。中继器允许您定义一个主要的模板,并在页面中重复使用该模板的实例。以下是中继器的作用和优缺点: 作…...

猫罐头哪个牌子好性价比高?五大性价比高的品牌推荐
很多猫奴担心猫咪天天吃干猫粮可能会导致营养不足,所以想给猫咪换换口味,改善一下饮食。这时,选择猫罐头是个不错的选择。不过,喂猫罐头也是有一些讲究的。 作为从业6年的宠物护理师来说,作为早在几年就开始接触猫罐头…...

宣布推出 ML.NET 3.0
作者:Jeff Handley 排版:Alan Wang ML.NET 是面向 .NET 开发人员的开源、跨平台的机器学习框架,可将自定义机器学习模型集成到 .NET 应用程序中。ML.NET 3.0 版本现已发布,其中包含大量新功能和增强功能! 此版本中的深…...

常见的排序算法---快速排序算法
快速排序算法 快排是基于分治的思想来的,快速排序就是在元素序列中选择一个元素作为基准值,每趟总数据元素的两端开始交替排序,将小于基准值的交换的序列前端,大于基准值的交换到序列后端,介于两者之间的位置称为基准值…...
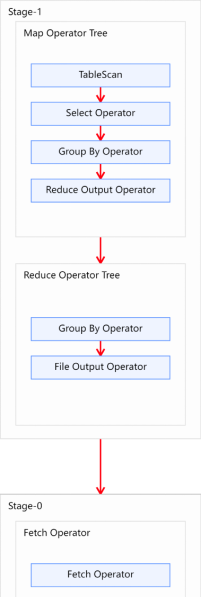
hive企业级调优策略之分组聚合优化
测试用表准备 hive企业级调优策略测试数据 (阿里网盘下载链接):https://www.alipan.com/s/xsqK6971Mrs 订单表(2000w条数据) 表结构 建表语句 drop table if exists order_detail; create table order_detail(id string comment 订单id,user_id …...

英码科技受邀参加2023计算产业生态大会,分享智慧轨道交通创新解决方案
12月13-14日,“凝心聚力,共赢计算新时代”——2023计算产业生态大会在北京香格里拉饭店成功举办。英码科技受邀参加行业数字化分论坛活动,市场总监李甘来先生现场发表了题为《AI哨兵,为铁路安全运营站好第一道岗》的精彩主题演讲&…...

【openssl】Linux升级openssl-1.0.1到1.1.1
文章目录 前言一、openssl是什么?二、使用步骤1.下载2.编译安装3.一些问题 总结 前言 记录一次openssl的升级,1.0.1升级到1.1.1 一、openssl是什么? OpenSSL是一个开源的加密工具包,广泛用于安全套接层(SSLÿ…...

美国联邦机动车安全标准-FMVSS
FMVSS标准介绍: FMVSS是美国《联邦机动车安全标准》,由美国运输部下属的国家公路交通安全管理局(简称NHTSA)具体负责制定并实施。是美国联邦政府针对机动车制定的安全标准,旨在提高机动车的安全性能,减少交通事故中的人员伤亡。F…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
