leetcode 974. 和可被 K 整除的子数组(优质解法)

代码:
class Solution {public int subarraysDivByK(int[] nums, int k) {HashMap<Integer,Integer> hashMap=new HashMap();hashMap.put(0,1);int count=0; //记录子数组的个数int last=0; //前一个下标的前缀和int now=0; //当前下标的前缀和for(int i=0;i<nums.length;i++){now=last+nums[i];int r=(now%k+k)%k;count+=hashMap.getOrDefault(r,0);hashMap.put(r,hashMap.getOrDefault(r,0)+1);last=now;}return count;}
}题解:
涉及到子数组的问题,我们一般采用滑动窗口或者前缀和来解决,滑动窗口适合解决数组中只有正数的题,而前缀和适合解决关于子数组之和的题,本题要判断哪些子数组的和能够被 k 整除,所以适合使用前缀和来解决
在解题之前,我们要先说明一个定理:同余定理,当(a - b)% c = n (整数) ,就能够推出 a % c = b % c ,这个定理是我们解题的要点,通过下图来说明解题的过程:
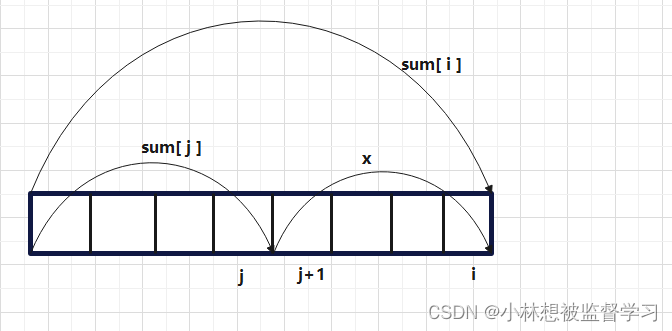
sum 是前缀和数组,如上图所示,x 是以 i 为尾符合条件的子数组之和,可以推出:sum[ i ] - sum[ j ] = x ,以及 x % k = 0 ,得到 (sum[ i ] - sum[ j ])% k = 0 ;根据同余定理,推得:sum[ i ] % k = sum[ j ] % k
j 是位于 0 ~ i -1 区间中的下标,也就是说在 0 ~ i -1 区间中,找到多少个符合上述条件的前缀和,就知道以 i 下标为尾,符合条件的子数组有多少
所以我们的思路就是用一个哈希表记录在 i 下标之前所有下标的前缀和 % k 的值对应的个数,以 sum[ i ] % k 为 key,个数为 value,从 0 下标开始遍历数组,在遍历到 i 下标时,我们已经知道了 i -1 下标的前缀和,i 下标的前缀和 sum[ i ] = sum[ i -1 ] +nums[ i ] ,通过 sum[ i ] % k 得到要在哈希表中寻找的 sum[ j ] % k 的值,在哈希表中 sum[ i ] % k 对应的值有多少个,就代表以 i 下标为尾,符合条件的子数组有多少个。
以该方法遍历所有的下标,便能得到所有符合条件的子数组的个数。
要注意一个细节,因为数组中存在负数,所以 sum[ i ] 可能为负数,在 java 中,负数 % 正数得到的是负数,为了去除负数的影响,所以在取模时不能直接用 sum[ i ] % k ,而是应该用式子 ( sum[ i ] % k + k)% k
还有一个细节,当哈希表初始化的时候要直接加上 key = 0,value = 1 的数据,因为不加上的话,就无法记录 nums[ i ] % k = 0 (符合条件的子数组只有 nums[ i ] 这一个数据)这种情况了
相关文章:

leetcode 974. 和可被 K 整除的子数组(优质解法)
代码: class Solution {public int subarraysDivByK(int[] nums, int k) {HashMap<Integer,Integer> hashMapnew HashMap();hashMap.put(0,1);int count0; //记录子数组的个数int last0; //前一个下标的前缀和int now0; //当前下标的前缀和for(int i0;…...

【技术】MySQL 日期时间操作
MySQL 日期时间操作 MySQL 系统时间MySQL 时间格式化MySQL 年月日时分秒周MySQL 日期计算时分秒时差日期差日期加减 MySQL 系统时间 now():系统时间,年月日时分秒current_date:系统时间,年月日current_time:系统时间&…...

测试理论知识三:测试用例、测试策略
1.测试用例 完全的测试是不可能的,对任何程序的测试必定是不完全的,那么,最显然的测试策略就是努力使测试尽可能完全。 进行测试前,推荐先使用黑盒测试的方法设计测试用例,然后使用白盒测试方法来补充的测试用例。 2…...
【clickhouse】在CentOS中离线安装clickhouse
https://packages.clickhouse.com/rpm/stable/ 通过如下命令检查是否安装过clickhouse [root172 ~]# rpm -qa | grep clickhouse 把rpm安装包放到opt/lzh目录 按照如下命令顺序安装 [root172 /]# rpm -ivh /opt/lzh/clickhouse-common-static-22.1.2.2-2.x86_64.rpm [root…...

微信商户号申请0.2费率
我们都知道,目前市场上的支付宝或者微信商户收款,无论是线上收款还是实体店收款,一般都采用0.6%的收款费率,1万元就是60元。 其实这不低的。 大多数线下实体店商家可能使用的聚合支付码可能是0.38%,1万元是38。 虽然不…...

基于单片机设计的电子指南针(LSM303DLH模块(三轴磁场 + 三轴加速度)
一、前言 本项目是基于单片机设计的电子指南针,主要利用STC89C52作为主控芯片和LSM303DLH模块作为指南针模块。通过LCD1602液晶显示屏来展示检测到的指南针信息。 在日常生活中,指南针是一种非常实用的工具,可以帮助我们确定方向࿰…...

深度学习 该用什么标准判断差异最小
决定差异最小的标准通常依赖于您的具体问题和任务。以下是一些常见的用于评估预测性能的标准和思路: 1. **均方根误差 (RMSE):** RMSE 是预测值和真实值之间差异的平方的平均值的平方根。它对较大的误差更加敏感。 from sklearn.metrics import mean_squared_error…...
汽车制造厂设备故障预测与健康管理PHM
在现代汽车制造工业中,设备的可靠性和稳定性对于保证生产线的高效运行至关重要。为了提高生产效率、降低维修成本以及确保产品质量,汽车制造厂逐渐采用设备故障预测与健康管理(PHM)系统,以实现对设备状态的实时监测和预…...
如何通过宝塔面板搭建一个MySQL数据库服务并实现无公网ip远程访问?
文章目录 前言1.Mysql服务安装2.创建数据库3.安装cpolar3.2 创建HTTP隧道 4.远程连接5.固定TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址 前言 宝塔面板的简易操作性,使得运维难度降低,简化了Linux命令行进行繁琐的配置,下面简单几步,通过宝塔面板cp…...
C++ Qt开发:TabWidget实现多窗体功能
Qt 是一个跨平台C图形界面开发库,利用Qt可以快速开发跨平台窗体应用程序,在Qt中我们可以通过拖拽的方式将不同组件放到指定的位置,实现图形化开发极大的方便了开发效率,本章将重点介绍TabWidget标签组件的常用方法及灵活运用。 Q…...

【轻量化篇】YOLOv8改进实战 | 更换主干网络 Backbone 之 RepGhostnet,重参数化实现硬件高效的Ghost模块
YOLOv8专栏导航:点击此处跳转 前言 轻量化网络设计是一种针对移动设备等资源受限环境的深度学习模型设计方法。下面是一些常见的轻量化网络设计方法: 网络剪枝:移除神经网络中冗余的连接和参数,以达到模型压缩和加速的目的。分组卷积:将卷积操作分解为若干个较小的卷积操…...

【STM32工具篇】使用CLion开发STM32
本文主要记录使用CLion开发STM32,并调试相关功能 使用的CLion版本:2023.3.1 CLion嵌入式配置教程:STM32CubeMX项目 |CLion 文档 (jetbrains.com) OpenOCD官网下载:Download OpenOCD for Windows (gnutoolchains.com) GNU ARM工…...

elementui中的el-table,当使用fixed属性时,table主体会遮挡住滚动条的大半部分,导致很难选中。
情况: 解决: el-table加个类,这里取为class"table" 然后是样式部分: <style scoped lang"scss"> ::v-deep.table {// 滚动条高度调整::-webkit-scrollbar {height: 15px;}// pointer-events 的基本信…...

鸿蒙端H5容器化建设——JSB通信机制建设
1. 背景 2023年鸿蒙开发者大会上,华为宣布为了应对国外技术封锁的潜在风险,2024年的HarmonyOS NEXT版本中将不再兼容Android,并推出鸿蒙系统以及其自研的开发框架,形成开发生态闭环。同时,在更高维度上华为希望将鸿蒙…...
数据管理平台Splunk Enterprise本地部署结合内网穿透实现远程访问
文章目录 前言1. 搭建Splunk Enterprise2. windows 安装 cpolar3. 创建Splunk Enterprise公网访问地址4. 远程访问Splunk Enterprise服务5. 固定远程地址 前言 Splunk Enterprise是一个强大的机器数据管理平台,可帮助客户分析和搜索数据,以及可视化数据…...

MaBatis使用`ResultMap`标签手动映射详解使用
文章目录 MaBatis使用ResultMap标签手动映射详解使用1、MyBatis只能自动维护库表”列名“与”属性名“相同时的对应关系,二者不同时无法自动ORM,如下:2、在SQL中使用 as 为查询字段添加列别名,以匹配属性名:但是如果我…...

openstack-keystone服务
文章目录 keystone服务安装和配置先决条件安装并配置组件运行以下命令来安装包。编辑文件 /etc/keystone/keystone.conf 并完成如下动作:初始化身份认证服务的数据库:初始化Fernet keys:Bootstrap the Identity service: 配置 Apache HTTP 服…...

大数据HCIE成神之路之数据预处理(3)——数值离散化
数值离散化 1.1 无监督连续变量的离散化 – 聚类划分1.1.1 实验任务1.1.1.1 实验背景1.1.1.2 实验目标1.1.1.3 实验数据解析 1.1.2 实验思路1.1.3 实验操作步骤1.1.4 结果验证 1.2 无监督连续变量的离散化 – 等宽划分1.2.1 实验任务1.2.1.1 实验背景1.2.1.2 实验目标1.2.1.3 实…...
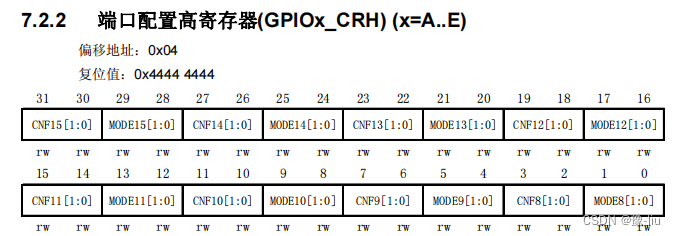
stm32 寄存器、地址、位带操作
存储器区域功能划分 4GB 的地址空间中,ARM 已经粗线条的平均分成了 8 个块,每块 512MB,每个块也都规定了用途,具体分类见表格 6-1。每个块的大小都有 512MB,显然这是非常大的,芯片厂商在每个块的范围内设计…...
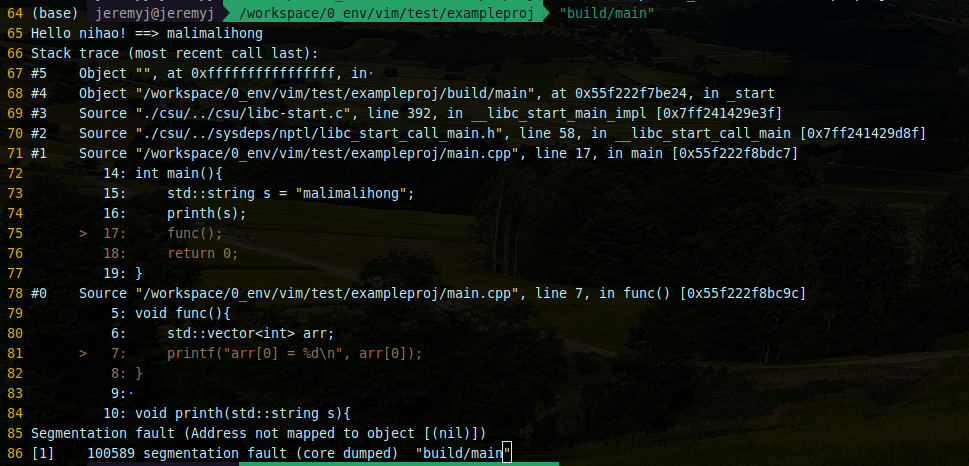
记录 | gdb使用backward-cpp来美化调试log
# 在当前工程目录下 git clone https://github.com/bombela/backward-cpp.git 编辑CMakeList.txt cmake_minimum_required(VERSION 3.15)project(exampleproj LANGUAGES CXX)add_subdirectory(backward-cpp)add_executable(main main.cpp)target_sources(main PUBLIC ${BACKW…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
