C语言数据结构-排序
文章目录
- 1 排序的概念及运用
- 1.1 排序的概念
- 1.2 排序的应用
- 2 插入排序
- 2.1 直接插入排序
- 2.2 希尔排序
- 2.3 直接排序和希尔排序对比
- 3 选择排序
- 3.1 堆排序
- 3.2 直接选择排序
- 4 交换排序
- 4.1 冒泡排序
- 4.2 快速排序
- 4.2.1 挖坑法1
- 4.2.2 挖坑法2
- 4.2.3 挖坑法3
- 5 并归排序
- 6 十万级别数据测试
1 排序的概念及运用
1.1 排序的概念
排序:使一串记录按照其中的某个或某些关键字的大小,递增或递减的排列的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
1.2 排序的应用
2 插入排序
从初始有序的序列开始,不断地把新的元素插入前面已经排好的序列中,当等待排序的数据元素都插入到前面排好的序列是,排序结束。这种排序方法就是“插入排序”。我们在这里讲“直接插入排序”和“希尔排序”。
2.1 直接插入排序
直接插入排序逐个处理待处理的元素,每个新元素与前面已排序的子序列中的元素进行比较将它插入到子序列中正确的位置。
对n个待排序的元素,直接插入排序先取出第二个元素,根据元素的值将其插入已排序的子序列(此时子序列只有第一个元素),再将第三个元素插入到前面已排序的子序列(此时子序列有第一个和第二个元素)中合适的位置,接下来每一个元素都是这样,知道最后一个元素为止。
直接插入排序的时间复杂度是O(n*n)
拿出来一个数组a[]={"91","67","31","62","30","72","46"},排序解析见下图。
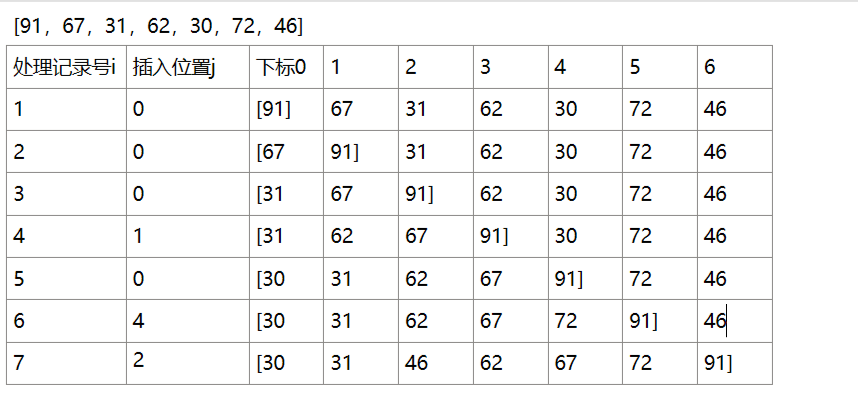
从下标i=0开始,最后一次进行比较时a[i-1]于a[n]比较,循环内i的范围就是
i<n-1
在子序列进行比较时,子序列的最大下标再最差情况下(逆序)正好满足循环次数,就设定了int end=i;,然后,a[end+1]与子序列进行比较,像上图所示
//1 插入排序,排序结果从小到大
void InsertSort(int* a, int n) //传入数组a,数组a的元素个数n
{for (int i = 0; i < n-1; i++){//end始终是一组循环内最后一个下标int end = i;//用t保存a[end+1]int t = a[end + 1];while (end >= 0){if (a[end] > t){//新元素的值小,下标end+1存放a[end]较大的数a[end + 1] = a[end];//end减一,继续在子循环中比较end--;}else{break;}}a[end + 1] = t; //退出while循环,这时候end的值或已改变,经while后比他大的值已经向后挪一位,填充a[end+1],这里体现提前保存a[end+1]的作用}
}
上述接口完成,我们进行测试,以下在编译器中测试:
再次封装,后续写入其他排序方法更方便调试。
#include<stdio.h>void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}void InsertSort(int* a, int n)
{for (int i = 0; i < n-1; i++){int end = i;//用t保存a[end+1]int t = a[end + 1];while (end >= 0){if (a[end] > t){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = t;}
}void TestInsertSort()
{int a[] = { 3,6,9,2,5,8,1,4,7 };InsertSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestInsertSort(); return 0;
}
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
2.2 希尔排序
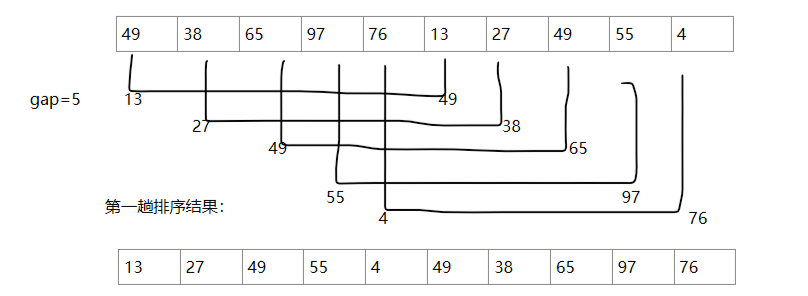
希尔排序又称缩小增量排序。直接插入排序的时间复杂度是O(n*n),但是,排序元素正序时,时间复杂度就是O(n),希尔排序将待排序元素变得“基本有序”,然后再调用直接插入排序完成最后的排序。
(1)实现过程:先选定一个比n小的整数gap,把待排序文件中所有记录分成gap个组(正好可以分成gap组),所有距离为gap的记录下来的元素分在同一组内,再对每一组内的记录进行排序。再取gap更小的数,直到gap为1,所有记录在同一组中进行直接插入排序。
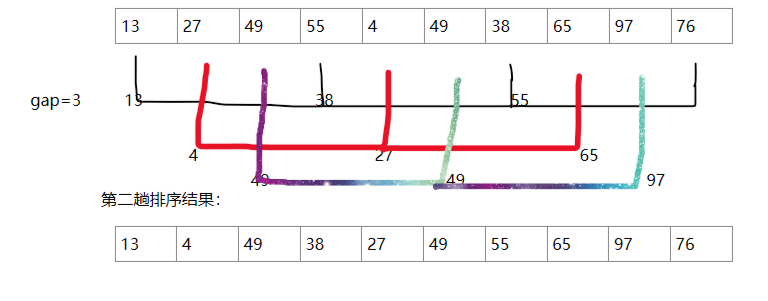

void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//分组,设置步长gapgap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int t = a[end + gap];while (end>=0){if (a[end] > t){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = t;}}
}void PrintArray(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}//封装成测试函数
void TestShellSort()
{int a[] = { 3,6,9,2,5,8,1,4,7 };ShellSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestShellSort();return 0;
}
2.3 直接排序和希尔排序对比
放置了测试的接口在release版本(测试比debug快)下,比较直接排序和希尔排序
void TestOP()
{srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);free(a1);free(a2);}
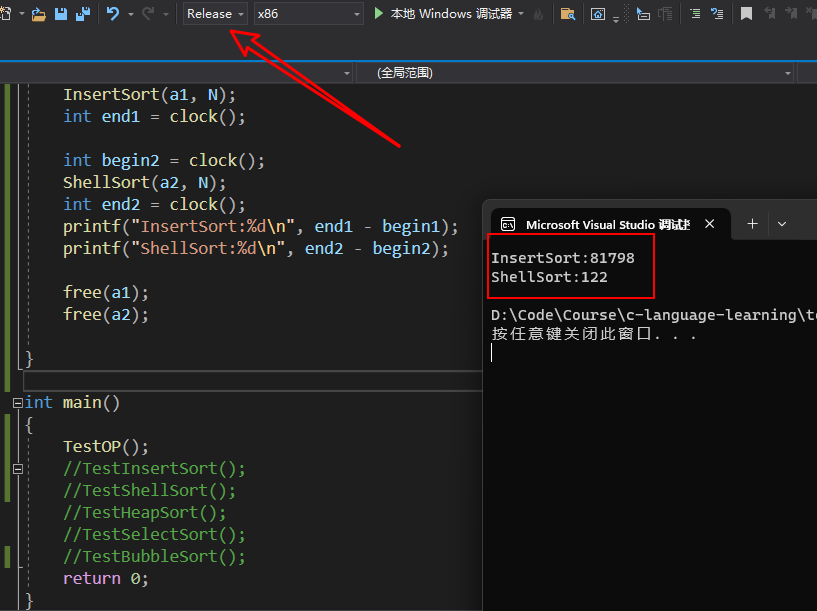
通过测试发现希尔排序处理上述百万级别的数据花了122ms,而直接插入排序耗时81798ms。

3 选择排序
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
3.1 堆排序
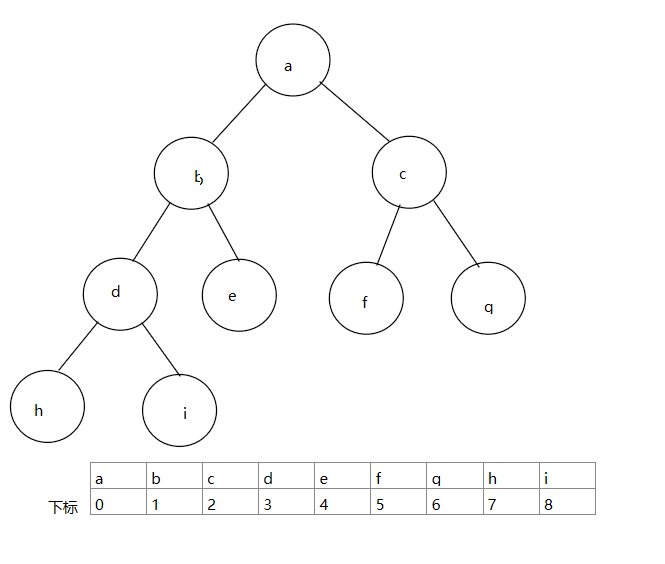
堆的逻辑结构是一颗完全二叉树,堆的物理机构是一个数组
我们通过下标父子节点关系发现小堆的特点
leftchild = parent * 2 + 1;
rightchild = parent * 2 + 2
堆的两个特性:
1 结构性:用数组表示的完全二叉树
2 有序性:任一节点的关键字是其子树的所有节点的最大值(或最小值)
最大堆(MaxHeap)可以保证根是最大值。大堆要求树中所有的父亲都大于等于孩子。
最小堆(MinHeap)可以保证根是最小值。小堆要求所有的父亲都小于等于孩子。
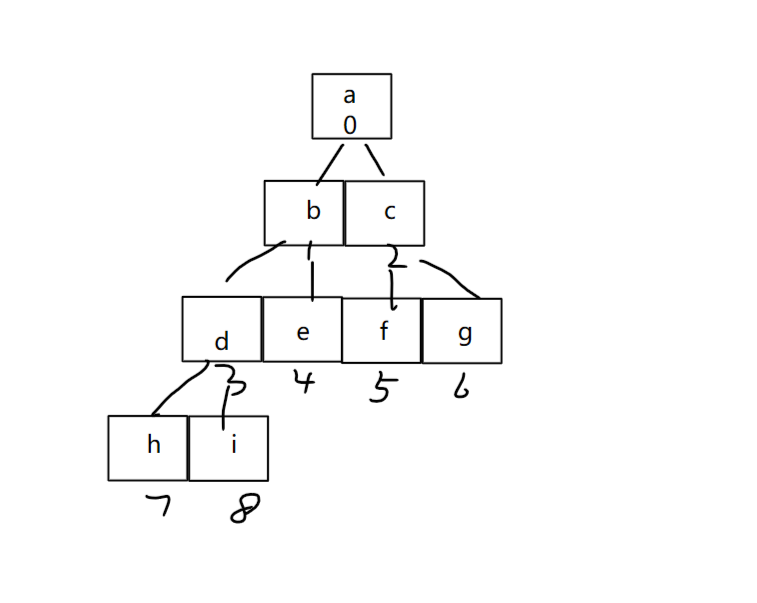
建小堆使用向下调整算法。
向下调整法是让父亲结点与其孩子节点进行比较,比父亲节点小就交换。一直调整,直到碰到叶子节点终止。当左右子树不是小堆,就不能直接使用向下调整算法了,怎么办?倒着从最后一棵非叶子节点开始调整
我们排列升序数组,是建立大堆!!!选择排序,通过堆来选树。如果建立小堆,最小值在堆顶被选出来,在剩下数中再选数,但是剩下树结构乱了,需要重新建堆。建堆的时间复杂度是O(n),那堆排序时间复杂度就是O(n*n)。我们建立大堆,最大的数与最小的交换位置。忽视最大数,只看剩下n-1个数,n-1个数向下调整,选出第二大的数,再跟倒数第二个数交换位置。再往下交换……
此时堆排序的时间复杂度就是O(nlogn)。
void Swap(int* p1, int* p2)
{int t = *p1;*p1 = *p2;*p2 = t;
}
//向下调整算法
void AdjustDwon(int* a, int n, int root)
{int parent = root;int child = parent * 2 + 1; //默认左孩子while (child<n){//选出左右节点中较大的一个if (child + 1 < n && a[child + 1] > a[child]){child += 1;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{//建堆for (int i = (n-1-1)/2; i >=0; i--){AdjustDwon(a, n, i);}int end = n - 1;while (end>0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);end--;}
}//封装测试函数
void TestHeapSort()
{int a[] = { 3,6,9,2,5,8,1,4,7 };HeapSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestHeapSort();return 0;
}堆排序的特性总结:
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
3.2 直接选择排序
在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换
在剩余的array[i]–array[n-2](array[i+1]–array[n-1])集合中,重复上述步骤,直到集合剩余1个元素
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin<end){int Min = begin;int Max = begin;for (int i = begin; i <= end; i++){if (a[i] < a[Min]){Min = i;}else if (a[i] > a[Max]){Max = i;}}Swap(&a[begin], &a[Min]);//begin和max重叠的时候,在上一步,begin和min交换了,此时min下标处才是maxif (begin == Max){Max = Min;}Swap(&a[Max], &a[end]);begin++;end--;}
}void TestSelectSort()
{int a[] = { 3,6,9,2,5,8,1,4,7 };SelectSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}
直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
4 交换排序
基本思想:根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
4.1 冒泡排序
这个就是两两比较,不再细说。
void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){int flag = 0;for (int j = 1; j < n - i; j++){if (a[j - 1] > a[j]){Swap(&a[j - 1], &a[j]);flag = 1;}}//不需要交换if (flag == 0){break;}}
}
冒泡排序的特性总结:
- 冒泡排序是一种非常容易理解的排序
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
4.2 快速排序
- 这个我迷糊了,先把课件笔记写上
基本思想:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
三数取中。对于基准值的选取,我们使用三数取中的思想,设计一个接口。
这样可以优化排序效率,解决在有序情况下,快排效率低的问题。
// 三数取中
int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}
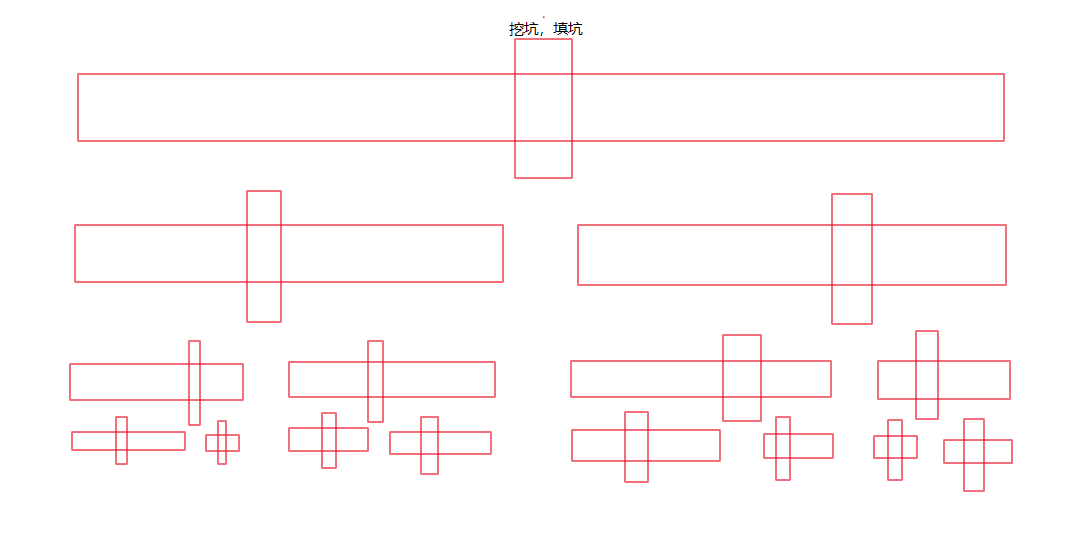
4.2.1 挖坑法1
挖坑法1
在无序区R1到R2中取一个作为基准,以此划分左右两个较小的无序子区:R1到Ri-1和Ri+1到Rn,且左边无序子区中关键字都小于等于基准,右侧的无序子区中记录的关键字均大于等于基准,而基准位于最终排序的位置上。这就是一个划分。然后各部分一直划分,知道整个序列按关键字有序排列。
// 挖坑法1
int PartSort1(int* a, int left, int right)
{int index = GetMidIndex(a, left, right);Swap(&a[left], &a[index]);int begin = left, end = right;int pivot = begin;int key = a[begin];// O(N)while (begin < end){// 右边找小,放到左边while (begin < end && a[end] >= key)--end;// 小的放到左边的坑里,自己形成新的坑位a[pivot] = a[end];pivot = end;// 左边找大while (begin < end && a[begin] <= key)++begin;// 大的放到左边的坑里,自己形成新的坑位a[pivot] = a[begin];pivot = begin;}pivot = begin;a[pivot] = key;return pivot;
}4.2.2 挖坑法2
挖坑法2 左右指针
选择begin找大,end找小,没有相遇就继续,相遇后交换。
// 挖坑法2
int PartSort2(int* a, int left, int right)
{int index = GetMidIndex(a, left, right);Swap(&a[left], &a[index]);int begin = left, end = right;int keyi = begin;while (begin < end){// 找小//begin < end在避免是升序的情况下,出现越界的情况while (begin < end && a[end] >= a[keyi]){--end;}// 找大while (begin < end && a[begin] <= a[keyi]){++begin;}Swap(&a[begin], &a[end]);}//相遇之后交换Swap(&a[begin], &a[keyi]);return begin;
}
4.2.3 挖坑法3
挖坑法3
prev找小,只要招到比下标keyi位置小的停下来,++prev,交换prev和cur位置,小的往前走,大的往后走。
注意避免自己跟自己交换的情况!
int PartSort3(int* a, int left, int right)
{int index = GetMidIndex(a, left, right);Swap(&a[left], &a[index]);int keyi = left;int prev = left, cur = left + 1;//结束条件while (cur <= right){//避免自己跟自己交换的情况if (a[cur] < a[keyi] && ++prev != cur){//++prev++;Swap(&a[prev], &a[cur]);}++cur;}Swap(&a[keyi], &a[prev]);return prev;
}快速排序
void QuickSort(int* a, int left, int right)
{if (left >= right)return;int keyIndex = PartSort3(a, left, right);// 小区间优化if (keyIndex - 1 - left > 10){QuickSort(a, left, keyIndex - 1);}else{InsertSort(a + left, keyIndex - 1 - left + 1);}if (right - (keyIndex + 1) > 10){QuickSort(a, keyIndex + 1, right);}else{InsertSort(a + keyIndex + 1, right - (keyIndex + 1) + 1);}
}
//未经优化版
//void QuickSort(int* a, int left, int right)
//{
// if (left >= right)
// return;
//
// int begin = left, end = right;
// int pivot = begin;
// int key = a[begin];
// // [left, right]
// // [left, pivot-1] pivot [pivot+1, right]
// // 左子区间和右子区间有序,我们就有序了,如果让他们有序呢? 分治递归
// QuickSort(a, left, pivot - 1);
// QuickSort(a, pivot + 1, right);
//}
测试函数
void TestQuickSort()
{//int a[] = { 6, 3, 5, 2, 7, 8, 9, 4, 1 };int a[] = { 49, 38, 65, 97, 76, 13, 27, 49, 13, 27, 49 };QuickSort(a, 0, sizeof(a) / sizeof(int)-1);PrintArray(a, sizeof(a) / sizeof(int));
}
快速排序的特性总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度:O(N*logN)
5 并归排序
基本思想:归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (left + right) >> 1;// 假设 [left, mid] [mid+1, right]//有序就归并_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);// 归并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}// 拷贝回去for (int i = left; i <= right; ++i){a[i] = tmp[i];}
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}void TestMergeSort()
{int a[] = { 10, 6, 7 ,1, 3, 9, 4, 2 };MergeSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
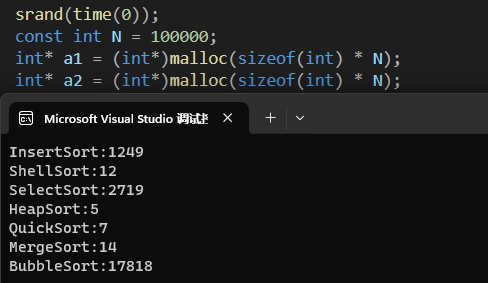
6 十万级别数据测试
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();//a1[i] = i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);}
在main()函数下测试结构如下:
相关文章:

C语言数据结构-排序
文章目录 1 排序的概念及运用1.1 排序的概念1.2 排序的应用 2 插入排序2.1 直接插入排序2.2 希尔排序2.3 直接排序和希尔排序对比 3 选择排序3.1 堆排序3.2 直接选择排序 4 交换排序4.1 冒泡排序4.2 快速排序4.2.1 挖坑法14.2.2 挖坑法24.2.3 挖坑法3 5 并归排序6 十万级别数据…...
Spring AOP入门指南:轻松掌握面向切面编程的基础知识
面向切面编程 1,AOP简介1.1 什么是AOP?1.2 AOP作用1.3 AOP核心概念 2,AOP入门案例2.1 需求分析2.2 思路分析2.3 环境准备2.4 AOP实现步骤步骤1:添加依赖步骤2:定义接口与实现类步骤3:定义通知类和通知步骤4:定义切入点步骤5:制作切面步骤6:将通知类配给…...

【顶级快刊】IEEE(Trans),审稿快仅2个月录用,入选CCF-B,现在投最快!
计算机类 • 好刊解读 今天小编带来IEEE旗下计算机领域顶刊,顶级快刊,CCF-B类推荐,如您有投稿需求,可作为重点关注!后文有相关领域真实发表案例,供您投稿参考~ 01 期刊简介 IEEE Transactions on Affect…...

深入浅出堆排序: 高效算法背后的原理与性能
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《linux深造日志》 《高效算法》 ⛺️生活的理想,就是为了理想的生活! 📋 前言 🌈堆排序一个基于二叉堆数据结构的排序算法,其稳定性和排序效率在八大排序中也…...

Golang实践录:gin绑定解析json的两种方法
本文介绍 Golang 的 gin 框架接收json数据并解析的2种方法。 起因及排查 某微服务工程,最近测试发现请求超时,由于特殊原因超时较短,如果请求处理耗时超过1秒则认为失败。排查发现,可能是gin接收解析json数据存在耗时,…...

Hypervisor Display架构
Hypervisor Display架构部分 1,所有LA侧的APP与显示相关的调用最终都会交由SurfaceFlinger处理 2,SurfaceFlinger会最终调用android.hardware.graphics.composer2.4-service服务 3,android.hardware.graphics.composer2.4-service服务会调用G…...
基于ssm二手车交易平台的设计论文
摘 要 进入21世纪网络和计算机得到了飞速发展,并和生活进行了紧密的结合。目前,网络的运行速度以达到了千兆,覆盖范围更是深入到生活中的角角落落。这就促使二手交易网站的发展。二手交易网站可以实现远程购物,远程选择喜欢的商品…...

IDEA 设置 SpringBoot logback 彩色日志(附配置文件)
1、背景说明 最开始使用 SpringBoot 时,控制台日志是带彩色的,让人眼前一亮😄 后来彩色莫名丢失,由于影响不大,一直没有处理。 2、配置彩色 最近找到了解决方法(其实是因为自定义 logback.xml࿰…...

数学建模学习笔记-皮尔逊相关系数
内容:皮尔逊相关系数 一.概念:是一个和线性线关的相关性系数 1.协方差概念: 协方差受到量纲的影响因此需要剔除 2.相关性的误区 根据这个结论,我们在计算该系数之前需要确定是否为线性函数 二.相关性的计算 1.Matlabÿ…...

随笔:集成学习:关于随机森林,梯度提升机的东拉西扯
1.集成学习 这里不会描述算法过程。 当我们有许多学习器对同一个任务做出判断,他们预测的概率可能各不相同,比如预测一个男生(小徐)会不会喜欢另一个女生(小雪),支持向量机算出来小徐爱上小雪的概率是0.8,朴素贝叶斯认为是0.3&a…...
多款实用个人年终总结模板,助力你的年度汇报!
临近年末,相信很多职场人这阵子都在忙着撰写个人年终总结,这份材料是对自己过去一年的工作进行的回顾和总结。撰写年终总结,其实也是一个非常重要的自我反思过程,可以帮助我们明确自己的目标,找出需要改进的地方&#…...
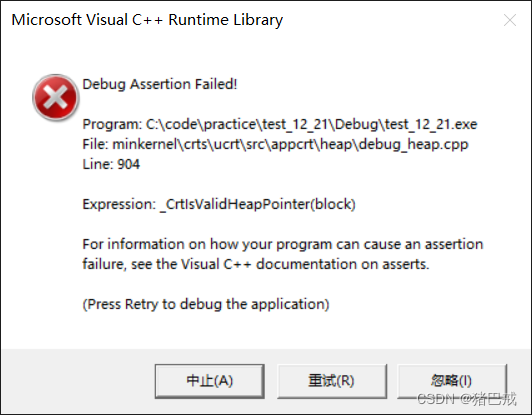
【C语言】动态内存管理基础知识——动态通讯录,如何实现通讯录容量的动态化
引言 动态内存管理的函数有:malloc,calloc,ralloc,free,本文讲解动态内存函数和使用,如何进行动态内存管理,实现通讯录联系人容量的动态化,对常见动态内存错误进行总结。 ✨ 猪巴戒:个人主页✨ 所属专栏:《C语言进阶》…...
配置Let‘s Encrypt (免费https证书))
Centos9(Stream)配置Let‘s Encrypt (免费https证书)
1. 安装snap,用来安装certbot: sudo dnf install epel-release sudo dnf upgrade sudo yum install snapd sudo systemctl enable --now snapd.socket sudo ln -s /var/lib/snapd/snap /snap snap install core snap refresh core 2. 安装 certbot命令…...
)
Spring之事务(2)
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

嵌入式科普(5)ARM GNU Toolchain相关概念和逻辑
一、目的/概述 二、资料来源 三、逻辑和包含关系 四、Arm GNU Toolchain最常用的命令 嵌入式科普(5)ARM GNU Toolchain相关概念和逻辑 一、目的/概述 对比高集成度的IDE(MDK、IAR等),Linux开发需要自己写Makefile等多种脚本。eclipse、Visual Studio等需要了解预处…...

Elasticsearch:什么是文本分类?
文本分类定义 - text classification 文本分类是一种机器学习,它将文本文档或句子分类为预定义的类或类别。 它分析文本的内容和含义,然后使用文本标签为其分配最合适的标签。 文本分类的实际应用包括情绪分析(确定评论中的正面或负面情绪&…...
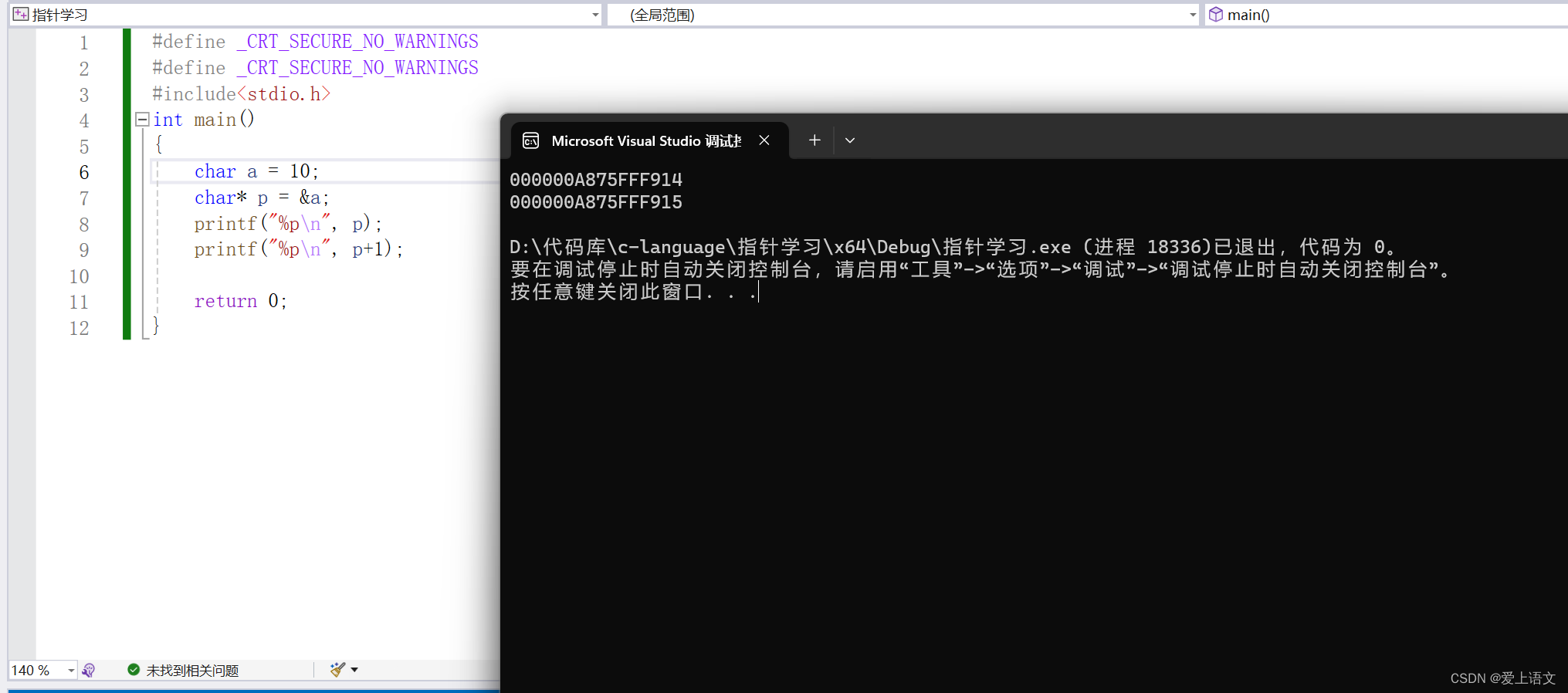
指针(3)
C语言昂,指针昂,最喜欢的一集,小时候学这一课我直接取地址了。上一篇博客给大家讲解了不同类型的指针变量的大小,今天来给大家讲解一下根据其所产生的一些性质。(往期回顾:指针(2)-C…...

外汇天眼:我碰到外汇投资骗局了吗?学会这5招,轻松识别外汇诈骗黑平台!
近年来外汇市场因为交易量大、流动性大、不容易被控盘、品种简单、风险相对低等特色,因此吸引不少投资人青睐,成为全球金融市场的热门选择。 然而,市面上充斥许多诈骗集团设立的黑平台,也打着投资外汇的名义行骗,不免会…...
一文解析子网掩码和默认网关,成为网络设置达人
随着互联网的普及,越来越多的人开始接触并使用电脑和网络。然而,对于很多初学者来说,网络设置中的子网掩码和默认网关是两个相对陌生的概念。今天,我们就来深入解析这两个概念,让你轻松掌握网络设置技巧! …...

二分查找法详解(6种变形)
前言 在之前的博客中,我给大家介绍了最基础的二分查找法(没学的话点我点我!) 今天我将带大家学习二分法的六种变形如何使用,小伙伴们,快来开始今天的学习吧! 文章目录 1,查找第一个…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...