机器学习:手撕 AlphaGo(一)

图 1-1: AphaGo 结构概览
1. 前言
AlphaGo 是一个非常经典的模型,不论从影响力还是模型设计上。它的技术迭代演进路径:AlphaGo,AlphaGoZero,AlphaZero,MuZero 更是十分精彩。相信有很多同学因为听了 AlphaGo 的故事对机器学习或者深度学习产生兴趣,致力投身于机器学习/深度学习的领域。本文尝试对 AlphaGo(即李世石版) 进行分析,看看当时在全世界范围内引起广泛关注的模型是如何设计的。同时我们也会对封面图进行解读,看看这张图里到底放生了什么故事。本文大致可以分为三个模块:
-
对计算机下围棋问题的分析和思考;
-
解释经典的 MCTS 思想;
-
介绍 AlphaGo 的算法内容。
文章比较长,祝有个精彩的旅程。
本文将尝试解释以下内容:
-
了解计算机下围棋的问题
-
MCTS 的基本原理
-
Policy Network
-
Value Network
-
AlphaGo 中的 MCTS
2. 计算机下围棋的问题描述
围棋是一个两人博弈的游戏,每个围棋选手均想战胜对方,这是一种两个人的零和游戏,即下棋的最后一定有一个胜利者和失败者 (和棋情况先不考虑)。在计算机诞生的早期,作为计算机的先驱,比较感兴趣的是:在下棋方向,计算机何时取代人类。所有的棋类游戏,对于人类来说都是一个思维活动的过程,然而计算机是一堆电子元器件堆积的产物,一个自然的问题:在棋类游戏中,由电子元器件组成的计算机如何模拟由生物细胞组成的人的思维方式呢?
2.1 计算机棋类游戏发展简史
要回答这个问题,不得不先看看计算机棋类游戏的发展史。可能在此过程中,会遇到不少的熟人,可能会惊叹他们在棋类游戏中,也做出了如此了不起的工作,也许对于他们来说,思考这个问题只是平时娱乐的游戏。首先 1950 是 Claude Shannon(香农) 提出用 Tree search(树搜索) 方式解决棋类问题,这点很重要,将棋类问题建模为 Tree, 将人类的思维过程建模为 Tree 上搜索的过程,在此我们先概略的体会它的重要性,在后续 MCTS 中将会看到这一个思想精彩的延展。然后 1953 年 Alan Turing(艾伦·图灵) 写出第一个国际象棋程序,这人同时也是我们的“祖师爷”。然后 Arthur Samuel 在前人的基础上,写出第一个跳棋游戏的程序,下的比它的开发者还好, 与此同时各个棋类的计算机程序,在飞速的发展,在 1968 年写出第一个击败围棋新手的程序。
因为前人已经将棋类游戏建模为 Tree Search 问题,不同棋类规则不同,从而树的规模不同,计算机擅长快速计算,普通的台式机计算能力在 129GFLOPS。所以问题转化为: 在棋类游戏中,计算机利用它的快速计算能力在 Tree Search 任务上,如何战胜人类选手,即各种棋类中,人类的最强选手。在 1992 年在西洋双陆棋中,IBM 开发的程序 TD-Gammon 仅次于人类的最佳选手,但它探索了很多人类未走过的策略,最终导致双陆器玩法的进步。1996 年在跳棋领域,程序 Chinook 赢得了美国的锦标赛冠军。然后就是部分同学知道的 IBM 的 DeepBlue(深蓝) 击败当时国际象棋的世界冠军 Garry Kasparov。最后是 2016 年就是大家熟知的 AlphaGo 击败人类九段选手李世石,因为当年围棋积分排行榜第一是柯洁,所以 AlphaGo 不算真正的击败人类最强选手,于是在 2017 年 AlphaGo Master 在乌镇击败当时的世界冠军柯洁。相当于宣布,在所有的棋类游戏中,计算机战胜了人类。

图 2-2: DeepBlue 作者与国际象棋世界冠军握手
2.2 围棋的规则简述
据说在所有的棋类游戏中,围棋的规则最简单,但却是最难玩的棋类游戏。我们先初步看下围棋的主要规则,有助于后续理解围棋的复杂性,以及感受当初 Deepmind 面对问题的难度。
-
围棋由 19 条横线和 19 条竖线组成的网格,共有 361 个交点,每个交点均是一个落子点,最开始时,棋盘上空无一子;
-
一个选手执黑色棋子,一个选手执白色棋子,在棋盘上轮流下,且执黑色棋子的选手先行;
-
当一片连续的同色的棋子完全被另外一种颜色的棋子包围时,这片连续棋子为“死棋”,将会被提走。如图 2-3c 所示,黑棋下在粉色区域,白色棋子将被提子;
-
当围棋结束时,统计黑白双方各自占据的交点,占据交点数量多的一 方获胜,如图 2-3d, 白色棋子占据 9 个交点,黑色棋子占据 16 个交点, 黑色棋子胜;
以上我们介绍这些规则,已经可以在盘面上演绎出千变万化的局面。面对这千变万化的局面,如果让我们“解决计算机围棋选手战胜人类围棋选手的问题”,我们该从何下手?

图 2-3:围棋的主要规则
2.3 计算机模拟人下围棋问题的难度
2.3.1 遍历围棋 Tree
借用 Claude Shannon(香农) Tree search 的思想,我们来建模围棋的 Tree。首先 Tree 的每个节点是一个符合围棋规则的棋盘状态。顺此推理,Tree 的根节点是一个空的棋盘,如图 2-4 所示。一个节点 s 的子节点是: 在节点 s 状态下,对方棋子所有的落子可能。在图 2-4 的棋盘中,根节点的子节点有 16 个,即黑棋落在 16 个交点的任意一个点,都是根节点的一个子节点,只不过其中有些子节点是“送人头”,人类选手不下在相应的位置上罢了,所以在图 2-4 中只描述节点常出现的子节点,一颗实际 (列出所有可能)的围棋 Tree 要比图 2-4 的 Tree 大很多。Tree 的叶子节点则是一场对弈中的终止状态,即在一场对弈中已经分出胜负。

图 2-4: 一颗简单的围棋 Tree
现在我们有了一颗围棋 Tree, 每个从根节点到叶子节点的路径,都是一盘有胜负的对弈,这颗 Tree 枚举了围棋中任何一种状态下所有可能的落子情况。那么计算机在与人类选手对弈时,参考这颗围棋 Tree,选择对自己有利的位置下棋。这样计算机完全立于不败之地,我们似乎解决了“计算机围棋选手战胜人类围棋选手的问题”,似乎没有 AlphaGo 什么事了。但我们都知道事实是 AlphaGo 战胜了人类。计算机借助围棋 Tree 下赢人类的推演逻辑是正确的,那什么地方没考虑到,才导致 Tree search 的思想出现 60 年后,计算机围棋选手才战胜人类职业选手呢?
2.3.2 围棋 Tree 节点太多
首先第一点,这棵围棋 Tree 很庞大。在标准棋盘下(19*19=361),我们简单估算一下枚举所有落子状态的 Tree 的节点个数。假设一场对弈最后,棋盘上每个点上都有棋子, 在一个空棋盘上,黑子的落子可能有 361 种,在黑子落下后,白子有 360 种落子可能,然后黑子有 359 种落子可能,白子 358 种落子可能... 以此类推下去, 倒数第二手白子有两种落子可能,最后一手黑子只有一种落子可能。很明显这是一个阶乘,即所有节点个数最多为 361!个。阶乘是一个增长速率很恐怖的运算,恐怖到阶乘的计算器都不计算 5000 或者 10000 以上的数的阶乘, 如图 2-5,可能因为计算结果太大,对人类已经没有使用价值了吧。

图 2-5: 随机抽取的阶乘计算器
361! 的计算结果如图 2-5d 所示,用科学计数法表示1.43∗,目前性能稍好些的 CPU 主频在 3GHz 左右,我们假设 1hz 查看一个 Tree 的节点,遍历完所有节点需要的年数用科学计数法表示,在 10 的指数上,只是比节点个数少 17 次方而已。我们估计节点个数的方法比较粗暴,在引入围棋规则后,节点个数大约
,比我们粗暴的估计方法减少很多。但这个值依然大的无法遍历 Tree。
2.3.3 很难判断一个节点的好坏
第二点我们忽略的难点:在围棋下完前的某个节点状态,很难判断谁赢谁输。这点也是导致“遍历围棋 Tree 的思想”不能实现的关键因素之一。也许在看完章节 2.3.2 后, 有的同学会说,围棋只有 361 个落子点,所以我们不需要查看围棋 Tree 所有的节点,我们只需要遍历每个选中节点的子节点就行,这样最多只需要查看
个节点,这个数值计算机可以很快算完。这个想法也是对的,在下棋时我们确实按照这个逻辑在 Tree 上搜索,只不过这个想法忽略的是:Tree search 过程需要比较节点 s 的所有子节点,然后在所有子节点中选择最有利于自己的子节点作为下一步的落子方案。因为针对围棋 Tree 上除叶子节点外任何一个单独的节点,我们不能判断输赢,即针对黑子 (或者白子) 判断不了当前局面的好坏。所以在落子前,必须先遍历围棋 Tree,由叶子节点向上,一层层计算出每个节点的值,这个节点值表示对黑子的有利程度,用于子节点比较时,找出最有利于自己的子节点。也许大家会好奇一个问题: 遍历围棋 Tree 时,如何计算每个节点的值?
2.3.4 计算围棋 Tree 中每个节点的值
在“遍历围棋 Tree 的思想”下,既然每个节点 s 有一个值 用于节点之间比较,那么借助图 2-6 我们来理解如何精确计算围棋 Tree 各个节点的值。如图 2-6a, 假设我们有一颗 5 层的简化的围棋 Tree, 只有叶子节点能判断胜负,如果黑子胜标记为 +1,如果白字胜标记为 −1。黑白棋子交替行棋,最开始由黑子先行。黑白棋子均会参考这颗围棋 Tree 行棋,而且每步行棋对自己来说都是最优策略,在此情况下我们计算每个节点的值
。根据我们的定义,
越大表示对黑子越有利,
越小表示对白子越有利。
的定义如式 2.1:

可以从以下 3 个方面理解式 2.1:
-
对于叶子节点 s,如果黑子胜,
= +1,如果白子胜
= −1;
-
对于非叶子节点 s, 若此轮到黑子行棋,为了让自己赢,
是所有子 节点中的最大值,行棋方案是最大值的子节点对应的动作 a;
-
对于非叶子节点 s, 若此轮到白子行棋,为了让自己赢,
是所有子 节点中的最小值,行棋方案是最小值的子节点对应的动作 a;
因为围棋中不是黑子赢就是白子赢,所以黑子和白子计算 的策略是相 反的。 根据公式 2.1 对
的定义, 现在我们再来看看图 2-6a 中这颗 5 层的围 棋 Tree, 由下到上如何一层层计算节点的值
。围棋 Tree 的第五层叶子 节点的值由黑子和白子的胜负自然得到;围棋 Tree 的第四层由白子行棋, 第四层中每个节点的值
为子节点中的最小值,于是便得到图 2-6b 的结 果;围棋 Tree 的第三层由黑子行棋,第三层中每个节点的值
为子节点中最大值,于是得到图 2-6c 的结果。第二层和第一层的节点依次类推计算, 便得到图 2-6d 的结果。这样我们便得到图 2-6 这颗 5 层的围棋 Tree 的所有 节点的值
。参照这种计算方法,我们可以计算任何一颗围棋 Tree 的节 点值
,有了一颗围棋 Tree 完整的节点值,我们就可以在这颗 Tree 上 search 了。只可惜真正棋盘的围棋 Tree 的
我们是计算不出来的。

图 2-6: 一颗围棋 Tree 节点值 v(s) 的计算过程
2.3.5 用近似求解代替精确求解
现在我们知道“遍历一颗围棋 Tree 的思想”为什么行不通了。那我们 是放弃还是继续攻克这个难题?针对个人讲,绝大多数人选择了放弃,只有 少部分人选择继续。针对全人类来讲,只要还有一个人在坚持探索计算机下 围棋,那么就等于没有放弃这个问题。AlphaGo 和 AlphaGo Zero 的出现, 也证明人类没有放弃这个问题,并且还解决了这个难题,让计算机围棋选手 战胜了人类围棋选手。继续回到我们的故事,在面临“遍历一颗围棋 Tree” 不现实的情况下,该如何继续我们的探索? 前辈们给出的答案: 我们不再追 求遍历一颗完整的围棋 Tree, 而是通过近似估计的方法,降低对围棋 Tree 深度和宽度的依赖。这种思想下最精彩的算法是 MCTS,我们在下一节将 详细介绍 MCTS,大家一起欣赏有关它的故事,看看这个算法是如何将“近 似解替代精确解的思想”发挥的淋漓尽致。
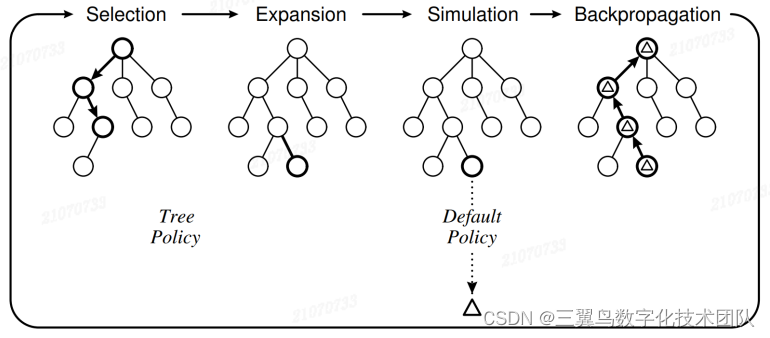
图 3-7: MCTS 概览
3. 团队介绍
「三翼鸟数字化技术平台-智慧设计团队」依托实体建模技术与人工智能技术打造面向家电的智能设计平台,为海尔特色的成套家电和智慧场景提供可视可触的虚拟现实体验。智慧设计团队提供全链路设计,涵盖概念化设计、深化设计、智能仿真、快速报价、模拟施工、快速出图、交易交付、设备检修等关键环节,为全屋家电设计提供一站式解决方案。
相关文章:

机器学习:手撕 AlphaGo(一)
图 1-1: AphaGo 结构概览 1. 前言 AlphaGo 是一个非常经典的模型,不论从影响力还是模型设计上。它的技术迭代演进路径:AlphaGo,AlphaGoZero,AlphaZero,MuZero 更是十分精彩。相信有很多同学因为听了 AlphaGo 的故事对…...
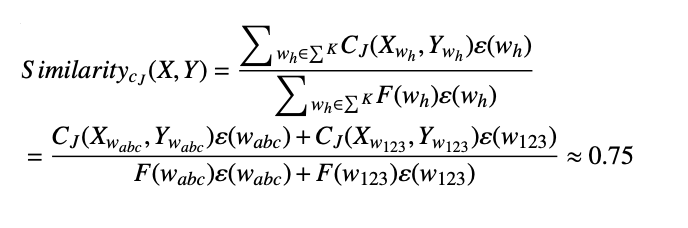
ElasticSearch学习篇9_文本相似度计算方法现状以及基于改进的 Jaccard 算法代码实现
背景 XOP亿级别题库的试题召回以及搜题的举一反三业务场景都涉及使用文本相似搜索技术,学习此方面技术以便更好的服务于业务场景。 目前基于集合的Jaccard算法以及基于编辑距离的Levenshtein在计算文本相似度场景中有着各自的特点,为了优化具体的计算时…...
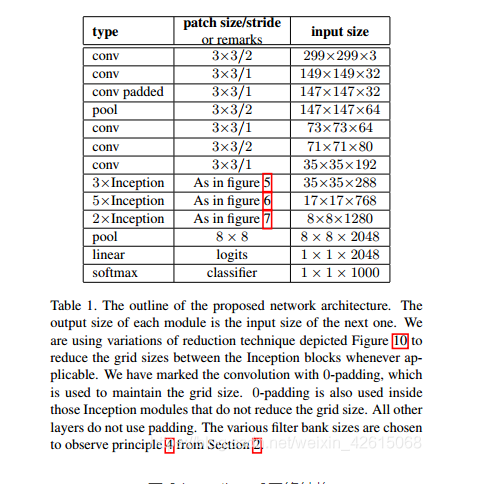
大创项目推荐 深度学习+python+opencv实现动物识别 - 图像识别
文章目录 0 前言1 课题背景2 实现效果3 卷积神经网络3.1卷积层3.2 池化层3.3 激活函数:3.4 全连接层3.5 使用tensorflow中keras模块实现卷积神经网络 4 inception_v3网络5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 *…...

Debezium系列之:Flink SQL消费Debezium数据格式,同步数据到下游存储系统
Debezium系列之:Flink SQL消费Debezium数据格式,同步数据到下游存储系统 一、Debezium二、依赖三、使用Debezium Format四、可用元数据五、Format参数六、重复的变更事件七、消费 Debezium Postgres Connector 产生的数据八、数据类型映射一、Debezium Debezium 是一个 CDC(…...

webrtc支持的最小宽度和高度
代码在:h264/sps_parser.cc // // IMPORTANT ONES! Now were getting to resolution. First we read the pic // width/height in macroblocks (16x16), which gives us the base resolution, // and then we continue on until we hit the frame crop offsets, wh…...

虚拟机对象的创建
虚拟机对象 虚拟机在Java堆中对象分配、布局和访问的访问过程 对象的创建 Java对象的创建步骤: 1)类加载检查 虚拟机遇到一条 new 指令时,首先将去检查这个指令的参数是否能在常量池中定位到这个类的符号引用,并且检查这个符号…...
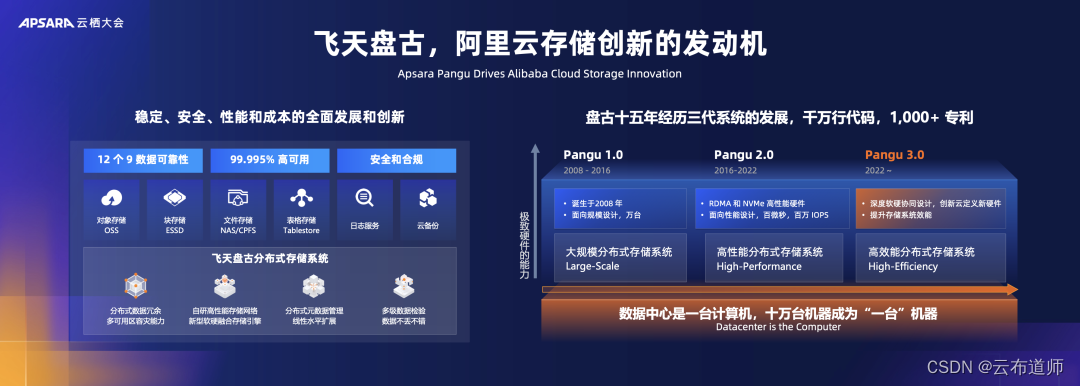
阿里云吴结生:云计算是企业实现数智化的阶梯
云布道师 近年来,越来越多人意识到,我们正处在一个数据爆炸式增长的时代。IDC 预测 2027 年全球产生的数据量将达到 291 ZB,与 2022 年相比,增长了近 2 倍。其中 75% 的数据来自企业,每一个现代化的企业都是一家数据公…...
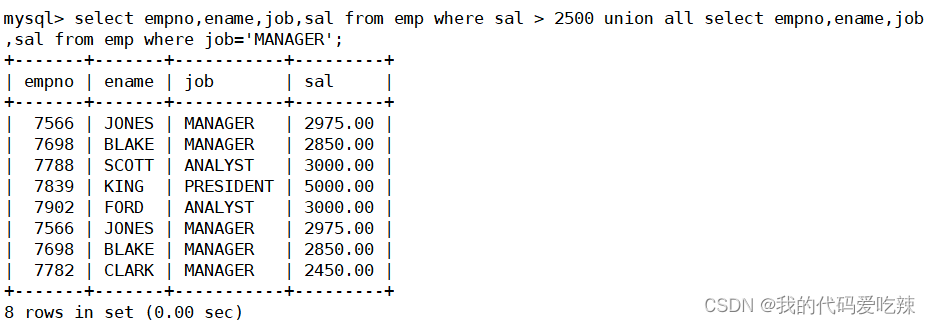
MySQL——复合查询
目录 一.基本查询回顾 二. 多表查询 三.自连接 四.子查询 1.单行子查询 2.多行子查询 3.多列子查询 4.在from子句中使用子查询 5.合并查询 一.基本查询回顾 准备数据库: 查询工资高于500或岗位为MANAGER的雇员,同时还要满足他们的姓名首字母为…...
)
mysql 23-3day 数据库授权(DCL)
目录 创建一个用户 并授权(grant)设置最大连接数客户端链接服务器创建用户删除用户修改用户修改密码root修改自己密码授予 mysql 权限收回权限收回权限刷新一下授权表mydql 知识点确保 mysql 用户为普通用户删除空口令账号安全建议 创建一个用户 并授权&…...

OpenHarmony之内核层解析~
OpenHarmony简介 技术架构 OpenHarmony整体遵从分层设计,从下向上依次为:内核层、系统服务层、框架层和应用层。系统功能按照“系统 > 子系统 > 组件”逐级展开,在多设备部署场景下,支持根据实际需求裁剪某些非必要的组件…...
Chatgpt如何共享可以防止封号!
ChatGPT 是一个基于 GPT-3.5/GPT-4 模型的对话系统,它主要用于处理自然语言对话。通过训练模型来模拟人类的语言行为,ChatGPT 可以通过文本交流与用户互动。每个新版本的 GPT 通常都会在模型规模、性能和其他方面有一些改进。在目前免费版GPT-3.5 中&…...

智能优化算法应用:基于社交网络算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于社交网络算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于社交网络算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.社交网络算法4.实验参数设定5.算法结果6.…...
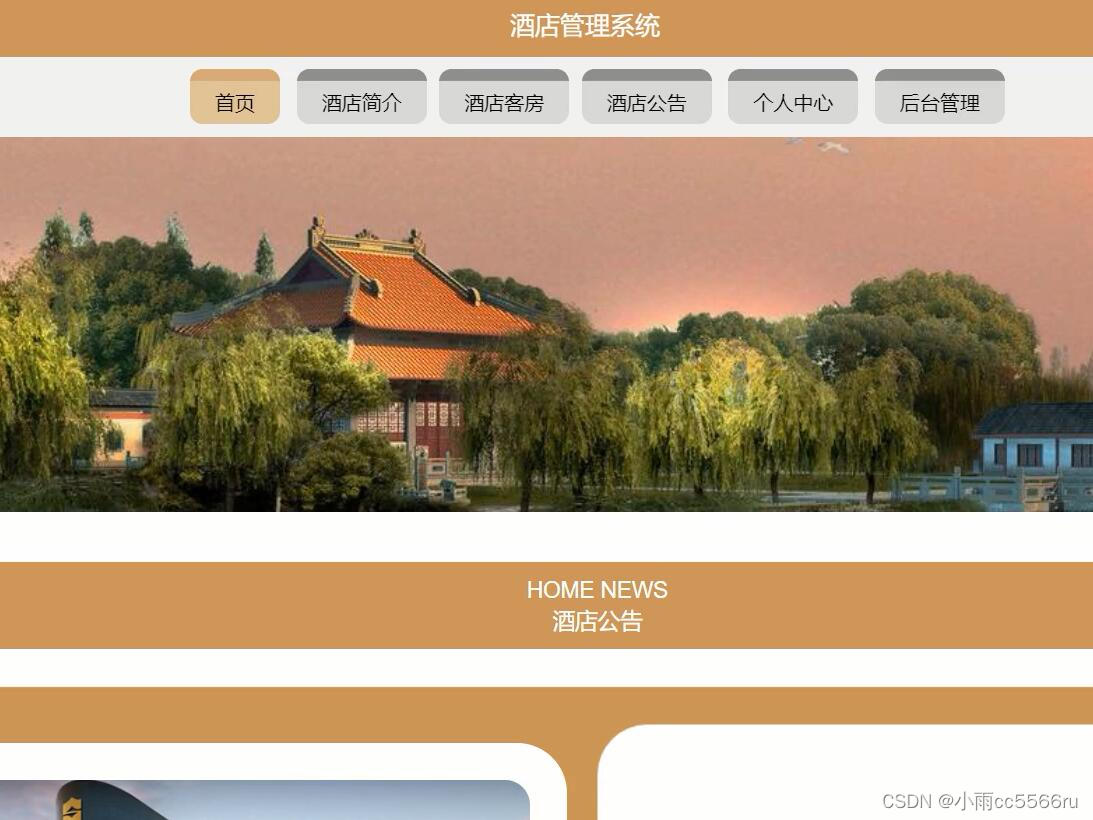
thinkphp+vue+mysql酒店客房管理系统 b1g8z
本系统包括前台界面、用户界面和管理员界面、员工界面。在前台界面里游客和用户可以浏览客房信息、公告信息等,用户可以预定客房,在用户中心界面里,用户可以管理预定信息,管理员负责用户预定的审核以及客房的发布、用户的入住等。…...

nodejs+vue+ElementUi摄影作品图片分享工作室管理系统
第1周 2.21~2.27 查阅资料,学习vscode开发平台和vue框架技术 第2周 2.28~3.6 对软件功能需求进行分析, 软件功能模块划分及软件界面设计 第3周 3.7~3.13 撰写并提交毕业设计开题报告、英文资料翻译 第4周 3.14࿵…...

详解FreeRTOS:专栏总述
目录 1、理论篇 2、基础篇 3、进阶篇 4、高级篇 5、拓展篇 本专栏基于FreeRTOS底层源码介绍了嵌入式实时操作系统的概念,FreeRTOS任务创建、任务调度、任务同步与消息传递,软件定时器、事件通知等知识。 主要分为5方面内容:理论篇、基础…...

在 linux 服务器上安装Redis数据库
先打开我们的Linux服务器 终端执行 安装redis sudo yum install redis然后 他会提示你要占多少磁盘空间 例如 我这里是 1.7 M 没问题就 y 然后回车就可以了 然后 我们这里执行 redis-cli --version这样 就能看到版本了 然后 我们可以根据版本选择启动命令 使用systemctl命…...

阿里云经济型、通用算力型、计算型、通用型、内存型云服务器最新活动报价
阿里云作为国内领先的云计算服务提供商,提供了多种规格的云服务器供用户选择。为了满足不同用户的需求,阿里云推出了经济型、通用算力型、计算型、通用型和内存型等不同类型的云服务器。下面将详细介绍这些云服务器的最新活动报价。 一、阿里云特惠云服…...

回溯算法 典型习题
vector<vector<int>> res; vector<int> path;void dfs() {if (递归终止条件){res.push_back(path);return;}// 递归方向for (xxx) {path.push_back(val);dfs();path.pop_back();} } 1.涉及枚举 2.不确定 for 循环的次数 总结 枚举各种可能的情况。 0.直接…...

14. 从零用Rust编写正反向代理, HTTP文件服务器的实现过程及参数
wmproxy wmproxy是由Rust编写,已实现http/https代理,socks5代理, 反向代理,静态文件服务器,内网穿透,配置热更新等, 后续将实现websocket代理等,同时会将实现过程分享出来ÿ…...

【随笔】MD5加密字符串、文件apache、springframework实现
文章目录 一、引入依赖二、工具代码三、测试代码四、输出结果 一、引入依赖 commons-codec <dependency><groupId>commons-codec</groupId><artifactId>commons-codec</artifactId><version>1.13</version> </dependency>二…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
