Leetcode算法系列| 4. 寻找两个正序数组的中位数
目录
- 1.题目
- 2.题解
- C# 解法一:合并List根据长度找中位数
- C# 解法二:归并排序后根据长度找中位数
- C# 解法三:方法二的优化,不真实添加到list
- C# 解法四:第k小数
- C# 解法五:从中位数的概念定义入手
1.题目
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
- 示例1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
- 示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
- 提示:
- nums1.length == m
- snums2.length == n
- 0 <= m <= 1000
- 0 <= n <= 1000
- 1 <= m + n <= 2000
- -10^6 <= nums1[i], nums2[i] <= 10^6
2.题解
C# 解法一:合并List根据长度找中位数
- 提new 一个 List , 并将 nums1 和 nums2 都添加到list 中,然后进行排序。对于排序后的 list, 根据长度计算出中位数的index,进而计算出最终结果。假设合并后的list长度为13,则从小到大第7个数字为中位数,resultIndex=6;假设合并后的list长度为14,则从小到大第7,8个数字的平均值为中位数,index 分别为 6,7,此时resultIndex =7,resultIndex-1 =6 , 结果为 ( list[resultIndex-1] + list[resultIndex] ) / 2.0 ;
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){int m = nums1.Length;int n = nums2.Length;int len = m + n;var resultIndex = len / 2;List<int> list = new List<int>(nums1);list.AddRange(nums2);list.Sort();if (len % 2 == 0){return (list[resultIndex - 1] + list[resultIndex]) / 2.0;}else{return list[resultIndex];}}
}

- 时间复杂度:O( (m+n)(1+log(m+n) ))
- 将长度为m,n的两个数组添加到list,复杂度分别为常数级的m和n ;list.Sort()的复杂度根据官方文档可得为 (m+n)log(m+n),所以该方法时间复杂度为 O( m+n+(m+n)log(m+n) ) = O( (m+n)(1+log(m+n) ))
- 空间复杂度:O(m+n)
- 使用list的长度为m+n.
C# 解法二:归并排序后根据长度找中位数
- 方法一使用了list.Sort() 方法,可以对list进行排序,但是,若题目给出的nums1 和 nums2 是无序数组,使用 list.Sort() 才算是 物有所用。 本题中 nums1 和 nums2 是有序数组,所以使用 list.Sort() 有写 杀鸡用宰牛刀的感觉,换句话说,这里面存在着效率的浪费。我们可以利用 【nums1 和 nums2 是有序数组】 这个条件,来精简我们的排序。
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){// nums1 与 nums2 有序添加到list中List<int> list = new List<int>();int i = 0, j = 0;int m = nums1.Length;int n = nums2.Length;int len = m + n;var resultIndex = len / 2;while (i < m && j < n){if (nums1[i] < nums2[j])list.Add(nums1[i++]);elselist.Add(nums2[j++]);}while (i < m) list.Add(nums1[i++]);while (j < n) list.Add(nums2[j++]);if (len % 2 == 0){return (list[resultIndex - 1] + list[resultIndex]) / 2.0;}else{return list[resultIndex];}}
}

- 时间复杂度:O(m+n)
- i 和 j 一起把长度为 m 和 n 的两个数组遍历了一遍,所以时间复杂度为 O(m+n)
- 空间复杂度:O(m+n)
- 使用list的长度为m+n.
C# 解法三:方法二的优化,不真实添加到list
- 对于方法二,我们在已知 resultIndex 的情况下,也可以不把 nums1 和 nums2 真实添加到 list 中,只需要在i 和 j 不断向右移动的过程中,计算是否到达了 resultIndex 即可。 若到达了 resultIndex,可以直接返回结果,而不必再处理后面的数据。但是相对的,我们需要在 i 或者 j 向右移动时,判断是否到达了resultIndex.
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){int i = 0, j = 0, m = nums1.Length, n = nums2.Length;int len = m + n;int resultIndex = len / 2;int resultIndexPre = resultIndex - 1;int result = 0, resultPre = 0; bool isTwoResult = len % 2 == 0;while (i < m || j < n){var nums1ii = i < m ? nums1[i] : int.MaxValue;var nums2jj = j < n ? nums2[j] : int.MaxValue;if (nums1ii < nums2jj){if (i + j == resultIndexPre) resultPre = nums1[i];if (i + j == resultIndex){result = nums1[i];if (isTwoResult) return (resultPre + result) / 2.0;else return result;}i++;}else{if (i + j == resultIndexPre) resultPre = nums2[j];if (i + j == resultIndex){result = nums2[j];if (isTwoResult) return (resultPre + result) / 2.0;else return result;}j++;}}return 0;}
}

- 时间复杂度:O(m+n)
- i 和 j 一起把长度为 m 和 n 的两个数组遍历了一半,但是每一步都需要判断当前i+j的值是否等于resultIndex,所以时间复杂度仍可认为 O(m+n)
- 空间复杂度:O(1)
- 对比方法二,不再使用list,只使用了几个变量来存值,所以空间复杂度为O(1)
C# 解法四:第k小数
- 前面的几种方法,时间复杂度都没有达到题目要求的 O(log(m+n)) 。 看到log,很明显需要使用二分法。根据 windliang提供的思路,题目求中位数,实际上是求第 k 小数的一种特殊情况,而求第 k 小数 有一种算法。
方法三中,i 和 j 每次向右移动一位时,相当于去掉了一个不可能是中位数的值,也就是一个一个的排除。由于给定的两个数组是有序的,所以我们完全可以一半一半的排除。假设我们要找第 k 小数,我们每次循环可以安全的排除掉 k/2 个数。
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){int n = nums1.Length;int m = nums2.Length;int len = n + m;int kPre = (len + 1) / 2;int k = (len + 2) / 2;if (len % 2 == 0)return (GetKth(nums1, 0, n - 1, nums2, 0, m - 1, kPre) + GetKth(nums1, 0, n - 1, nums2, 0, m - 1, k)) * 0.5;elsereturn GetKth(nums1, 0, n - 1, nums2, 0, m - 1, k);}private int GetKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k){int len1 = end1 - start1 + 1;int len2 = end2 - start2 + 1;//让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1 if (len1 > len2) return GetKth(nums2, start2, end2, nums1, start1, end1, k);if (len1 == 0) return nums2[start2 + k - 1];if (k == 1) return Math.Min(nums1[start1], nums2[start2]);int i = start1 + Math.Min(len1, k / 2) - 1;int j = start2 + Math.Min(len2, k / 2) - 1;if (nums1[i] > nums2[j])return GetKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));elsereturn GetKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));}
}

- 时间复杂度:O(log(m+n))
- i每进行依次循环,就减少 k/2个元素,所以时间复杂度为 O(log(k)) , 而 k = (m+n)/2 , 所以最终复杂度是 O(log(m+n))
- 空间复杂度:O(1)
- 只使用了几个变量来存值,递归是尾递归不占用堆栈, 所以空间复杂度为O(1)
C# 解法五:从中位数的概念定义入手
- 该方法参考了 LeetCode 题解的 官方题解 以及 windliang 的题解。
首先我们来看一下百度百科中位数的定义:https://baike.baidu.com/item/%E4%B8%AD%E4%BD%8D%E6%95%B0/3087401?fr=aladdin
public class Solution {public double FindMedianSortedArrays(int[] A, int[] B){int m = A.Length;int n = B.Length;//保证第一个数组是较短的if (m > n) return FindMedianSortedArrays(B, A);//正在寻找的范围为 [ A[iMin],A[iMax] ) , 左闭右开。二分查找取i=(iMin+iMax)/2int iMin = 0, iMax = m;while (iMin <= iMax){int i = (iMin + iMax) / 2;int j = (m + n + 1) / 2 - i;if (j != 0 && i != m && B[j - 1] > A[i]){ // i 需要增大iMin = i + 1;}else if (i != 0 && j != n && A[i - 1] > B[j]){ // i 需要减小iMax = i - 1;}else{ // 达到要求,并且将边界条件列出来单独考虑int maxLeft = 0;if (i == 0) { maxLeft = B[j - 1]; }else if (j == 0) { maxLeft = A[i - 1]; }else { maxLeft = Math.Max(A[i - 1], B[j - 1]); }if ((m + n) % 2 == 1) { return maxLeft; } // 奇数的话不需要考虑右半部分int minRight = 0;if (i == m) { minRight = B[j]; }else if (j == n) { minRight = A[i]; }else { minRight = Math.Min(B[j], A[i]); }return (maxLeft + minRight) / 2.0; //如果是偶数的话返回结果}}return 0.0;}
}

- 时间复杂度:O(log(min(m,n))
- 我们对较短的数组进行了二分查找,所以时间复杂度是 O(log(min(m,n))
- 空间复杂度:O(1)
- 只使用了几个变量来存值,所以空间复杂度为O(1)
相关文章:

Leetcode算法系列| 4. 寻找两个正序数组的中位数
目录 1.题目2.题解C# 解法一:合并List根据长度找中位数C# 解法二:归并排序后根据长度找中位数C# 解法三:方法二的优化,不真实添加到listC# 解法四:第k小数C# 解法五:从中位数的概念定义入手 1.题目 给定两个…...

Java整合APNS推送消息-IOS-APP(基于.p12推送证书)
推送整体流程 1.在开发者中心申请对应的证书(我用的是.p12文件) 2.苹果手机用户注册到APNS,APNS将注册的token返回给APP(服务端接收使用)。 3.后台服务连接APNS,获取连接对象 4.后台服务构建消息载体 5.后台…...

C语言strcpy函数用法
C语言strcpy函数用法 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一起深入了解C语言中的strcpy函数,这是一个在字符串处理中非…...
汽车服务品牌网站建设的作用是什么
汽车服务涵盖多个层面,在保修维护这一块更是精准到了车内车外,无论是品牌商还是市场中各维修部,都能给到车辆很好的维修养护服务。如今车辆的人均拥有量已经非常高,也因此市场中围绕汽车相关的从业者也比较多。 首先就是拓客引流…...
【iOS】UICollectionView
文章目录 前言一、实现简单九宫格布局二、UICollectionView中的常用方法和属性1.UICollectionViewFlowLayout相关属性2.UICollectionView相关属性 三、协议和代理方法:四、九宫格式的布局进行升级五、实现瀑布流布局实现思路实现原理代码调用顺序实现步骤实现效果 总…...
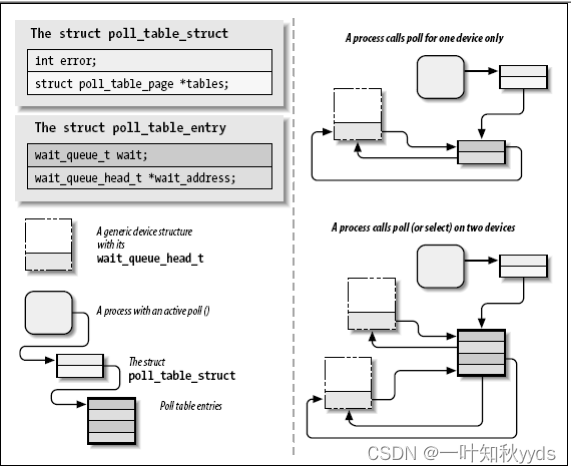
Linux poll 和 select 机制
poll select 介绍 使用非阻塞 I/O 的应用程序常常使用 poll, select, 和 epoll 系统调用. poll, select 和 epoll 本质上有相同的功能: 每个允许一个进程来决定它是否可读或者写一个 或多个文件而不阻塞. 这些调用也可阻塞进程直到任何一个给定集合的文件描述符可用来 读或写.…...
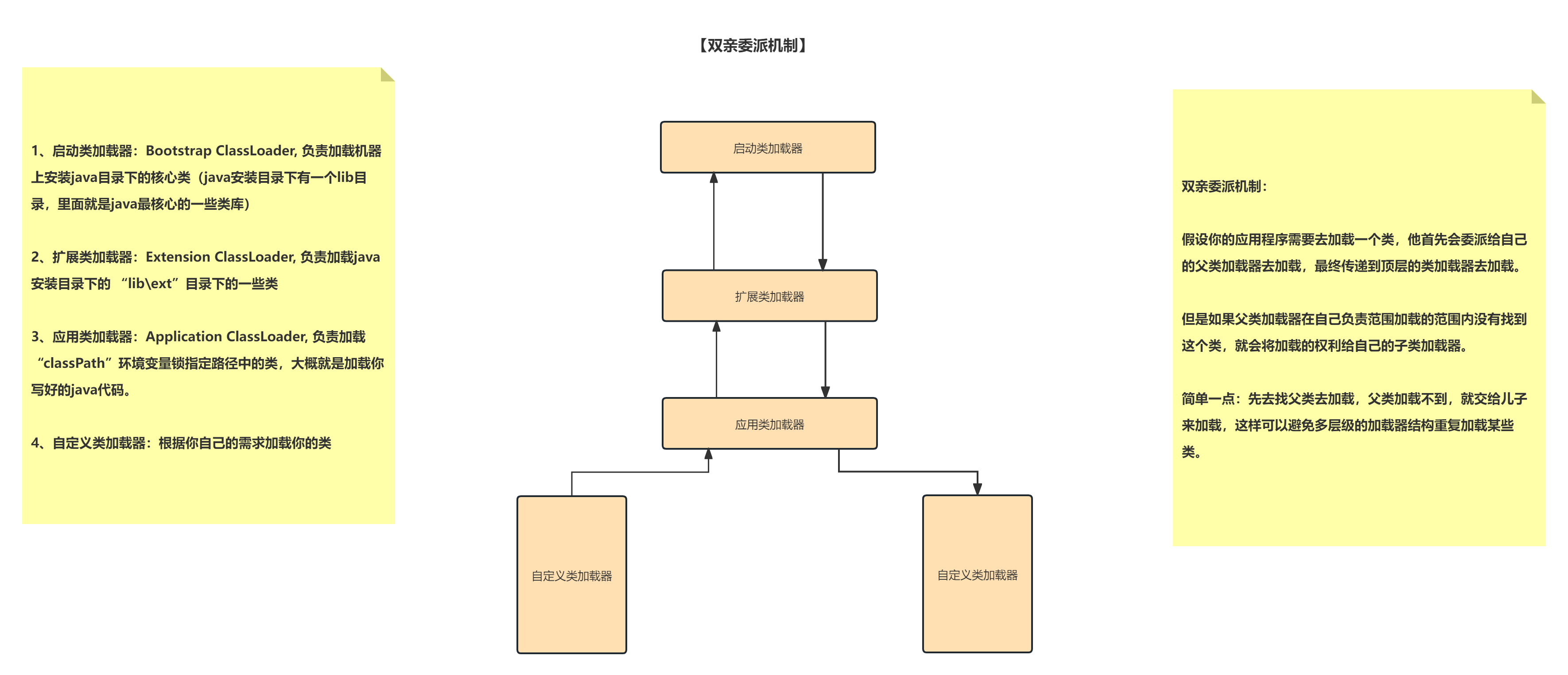
【JVM基础】 JVM 如何加载一个类以及类加载机制
文章目录 1、什么时候一个类会被加载?1、包含 main 方法的主类2、非 包含 main 方法的主类,什么时候去加载? 3、类加载器如何加载一个类?1、验证阶段:2、准备阶段:3、解析阶段:4、初始化&#x…...

Android Studio使用Genymotion
1. Genymotion介绍 GenyMotion速度之快令人发指,模拟效果堪比真机调试,支持绝大部分的模拟器功能,甚至包括语音,Google Now,支持eclipse, android studio。非常适合用来开发和演示效果。 2. Genymotion下载 Genymotio…...

Mysql sql_mode参数配置
今天在使用数据库查询时使用了Group语句,遇到问题: SELECT t1.UnderlyingInstrumentID, t2.* FROM t_OptionInstrument t1 LEFT JOIN t_Instrument t2 ON t2.InstrumentID t1.UnderlyingInstrumentID GROUP BY t1.UnderlyingInstrumentID > 1055 - …...

SpringIOC之AbstractMessageSource
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

详解Vue3中的基础路由和动态路由
本文主要介绍Vue3中的基础路由和动态路由。 目录 一、基础路由二、动态路由 Vue3中的路由使用的是Vue Router库,它是一个官方提供的用于实现应用程序导航的工具。Vue Router在Vue.js的核心库上提供了路由的功能,使得我们可以在单页应用中实现页面的切换、…...
)
Mysql四种事务隔离级别(简易理解)
读未提交:简单理解就是读到没有提交事务的执行结果;读已提交:简单理解就是只能读到已经提交的事务执行结果;可重复读:简单理解就是确保并发读取数据库时,读到的数据一致,这是mysql默认隔离级别&…...
react中使用redux最简单最方便的方式,配合rematch简化操作,5分钟学会
react中使用状态管理的方式也很多,比如redux和mobx等,今天这一片就讲一下redux的入门到熟练使用,主要是要理解它redux的组成有哪些,到怎么创建,和组建中怎么使用三个问题。这里先放上官网文档,不理解的地方…...
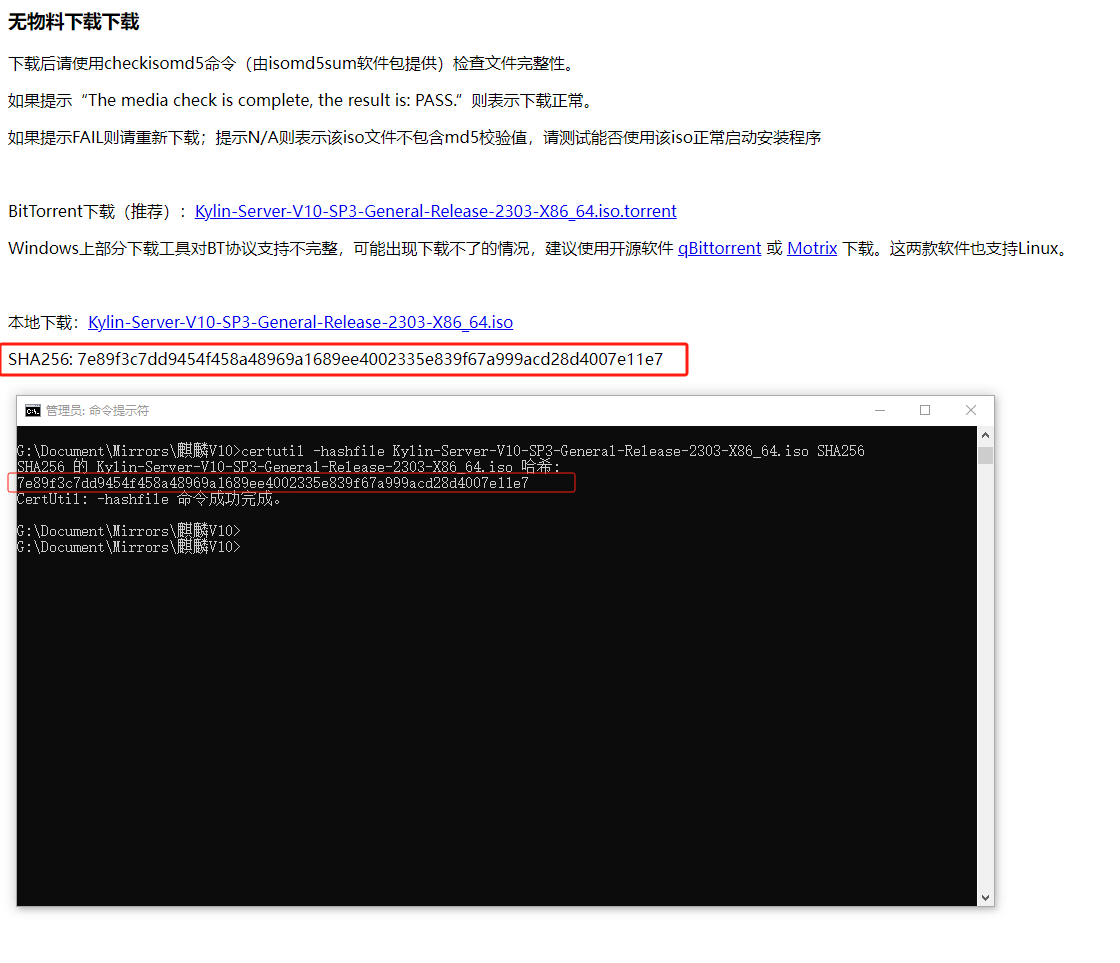
vmware安装中标麒麟高级服务器操作系统软件 V7.0操作系统
vmware安装中标麒麟高级服务器操作系统软件 V7.0操作系统 1、下载中标麒麟高级服务器操作系统软件 V7.0镜像2、安装中标麒麟高级服务器操作系统软件 V7.0操作系统 1、下载中标麒麟高级服务器操作系统软件 V7.0镜像 官方提供使用通道 访问官网 链接: https://www.kylinos.cn/ 下…...

OpenCV | 霍夫变换:以车道线检测为例
霍夫变换 霍夫变换只能灰度图,彩色图会报错 lines cv2.HoughLinesP(edge_img,1,np.pi/180,15,minLineLength40,maxLineGap20) 参数1:要检测的图片矩阵参数2:距离r的精度,值越大,考虑越多的线参数3:距离…...

【C#与Redis】--目录
1. 介绍 2. Redis 数据结构 3. Redis 命令 3.1 基本命令 3.2 字符串命令 3.3 哈希命令 3.4 列表命令 3.5 集合命令 3.6 有序集合命令 4. C# 操作 Redis 4.1 使用 Redis 库 4.2 连接 Redis 服务器 4.3 操作 Redis 数据结构 4.5 执行 Redis 命令 5. 高级主题 5.1 Redis 事…...

html旋转相册
一、实验题目 做一个旋转的3d相册,当鼠标停留在相册时,相册向四面散开 二、实验代码 <!DOCTYPE html> <html lang"zh"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" con…...

Plantuml之对象图语法介绍(十九)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
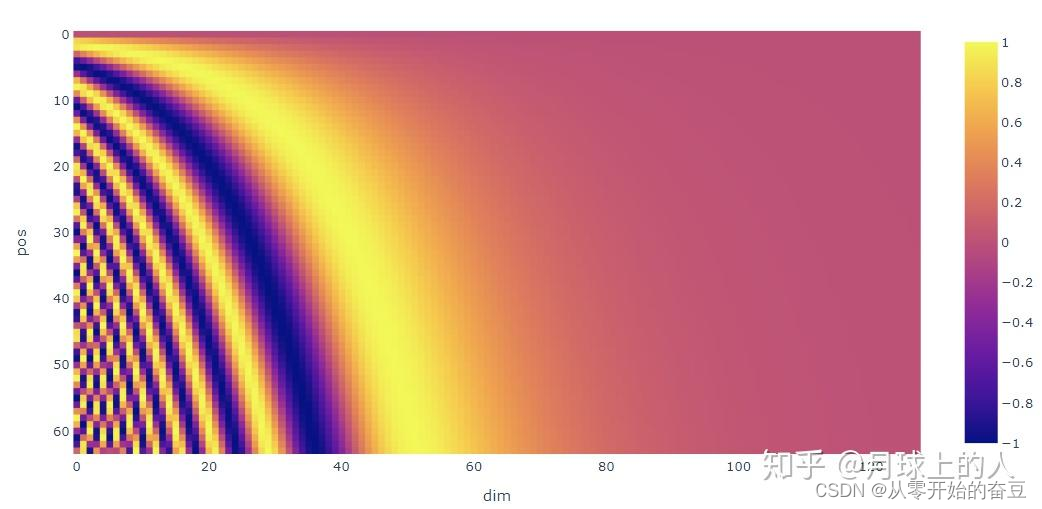
深度学习(八):bert理解之transformer
1.主要结构 transformer 是一种深度学习模型,主要用于处理序列数据,如自然语言处理任务。它在 2017 年由 Vaswani 等人在论文 “Attention is All You Need” 中提出。 Transformer 的主要特点是它完全放弃了传统的循环神经网络(RNN&#x…...
, Filter(), Find(), Map(), Negate(), Position())
R语言中的函数28:Reduce(), Filter(), Find(), Map(), Negate(), Position()
文章目录 介绍Reduce()实例 Filter()实例 Find()实例 Map()实例 Negate()实例 Position()实例 介绍 R语言中的Reduce(), Filter(), Find(), Map(), Negate(), Position()是base包中的一些高级函数。随后,很多包也给这些函数提供了更多的扩展。 Reduce() 该函数根…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

轻量级Docker管理工具Docker Switchboard
简介 什么是 Docker Switchboard ? Docker Switchboard 是一个轻量级的 Web 应用程序,用于管理 Docker 容器。它提供了一个干净、用户友好的界面来启动、停止和监控主机上运行的容器,使其成为本地开发、家庭实验室或小型服务器设置的理想选择…...
