高级人工智能之群体智能:蚁群算法
群体智能
鸟群:

鱼群:

1.基本介绍
蚁群算法(Ant Colony Optimization, ACO)是一种模拟自然界蚂蚁觅食行为的优化算法。它通常用于解决路径优化问题,如旅行商问题(TSP)。
蚁群算法的基本步骤
初始化:设置蚂蚁数量、信息素重要程度、启发因子重要程度、信息素的挥发速率和信息素的初始量。
构建解:每只蚂蚁根据概率选择下一个城市,直到完成一次完整的路径。
更新信息素:在每条路径上更新信息素,通常新的信息素量与路径的质量成正比。
迭代:重复构建解和更新信息素的步骤,直到达到预设的迭代次数。
2.公式化蚁群算法
-
转移概率 P i j k P_{ij}^k Pijk 表示蚂蚁 k k k从城市 i i i转移到城市 j j j的概率。它是基于信息素强度 τ i j \tau_{ij} τij(信息素重要程度为 α \alpha α和启发式信息 η i j \eta_{ij} ηij)(启发式信息重要程度为 β \beta β )计算的:
P i j k = [ τ i j ] α ⋅ [ η i j ] β ∑ l ∈ allowed k [ τ i l ] α ⋅ [ η i l ] β P_{ij}^k = \frac{[\tau_{ij}]^\alpha \cdot [\eta_{ij}]^\beta}{\sum_{l \in \text{allowed}_k} [\tau_{il}]^\alpha \cdot [\eta_{il}]^\beta} Pijk=∑l∈allowedk[τil]α⋅[ηil]β[τij]α⋅[ηij]β
其中, allowed k \text{allowed}_k allowedk 是蚂蚁 k k k 可以选择的下一个城市集合。
-
信息素更新规则。在每次迭代结束后,所有路径上的信息素会更新。更新规则通常包括信息素的挥发和信息素的沉积:
τ i j ← ( 1 − ρ ) ⋅ τ i j + Δ τ i j \tau_{ij} \leftarrow (1 - \rho) \cdot \tau_{ij} + \Delta \tau_{ij} τij←(1−ρ)⋅τij+Δτij
其中,( ρ \rho ρ ) 是信息素的挥发率,( Δ τ i j \Delta \tau_{ij} Δτij ) 是本次迭代中所有蚂蚁在路径 ( i , j ) (i, j) (i,j) 上留下的信息素总量,通常计算方式为_
Δ τ i j = ∑ k = 1 m Δ τ i j k \Delta \tau_{ij} = \sum_{k=1}^{m} \Delta \tau_{ij}^k Δτij=∑k=1mΔτijk
而对于每只蚂蚁 k k k ,在路径 ( i , j ) (i, j) (i,j) 上留下的信息素量 Δ τ i j k \Delta \tau_{ij}^k Δτijk 通常与其走过的路径长度成反比:
Δ τ i j k = { Q L k , if ant k travels on edge ( i , j ) 0 , otherwise \Delta \tau_{ij}^k= \begin{cases} \frac{Q}{L_k}, & \text{if ant } k \text{ travels on edge } (i, j) \\ 0, & \text{otherwise} \end{cases} Δτijk={LkQ,0,if ant k travels on edge (i,j)otherwise
这里, Q Q Q是一个常数, L k L_k Lk是蚂蚁 k k k的路径长度。
-
启发式信息 ( η i j \eta_{ij} ηij ) 通常是目标函数的倒数,例如在TSP问题中,它可以是两城市间距离的倒数:
η i j = 1 d i j \eta_{ij} = \frac{1}{d_{ij}} ηij=dij1
其中, d i j d_{ij} dij 是城市 i i i和 j j j 之间的距离。
这些公式构成了蚁群算法的数学基础。通过调整参数 α \alpha α , β \beta β, 和 ρ \rho ρ,可以控制算法的搜索行为,从而适应不同的优化问题。
3.代码实现
import numpy as np
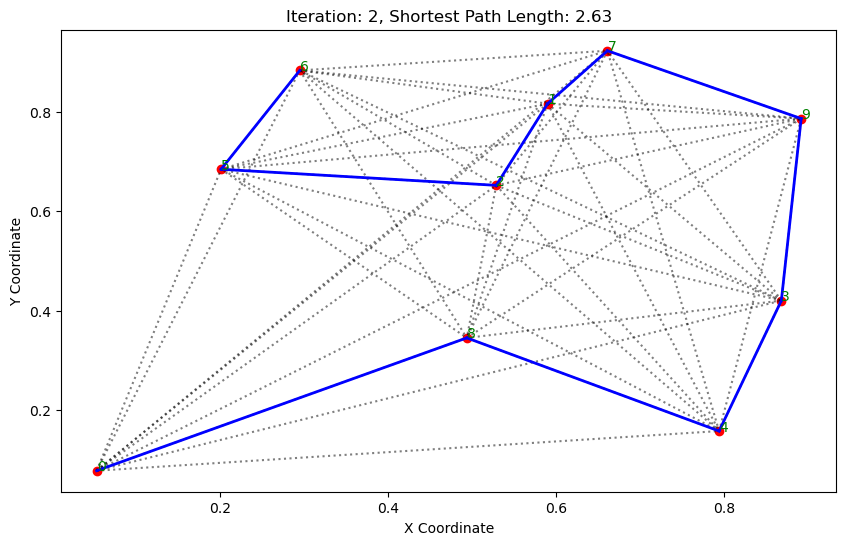
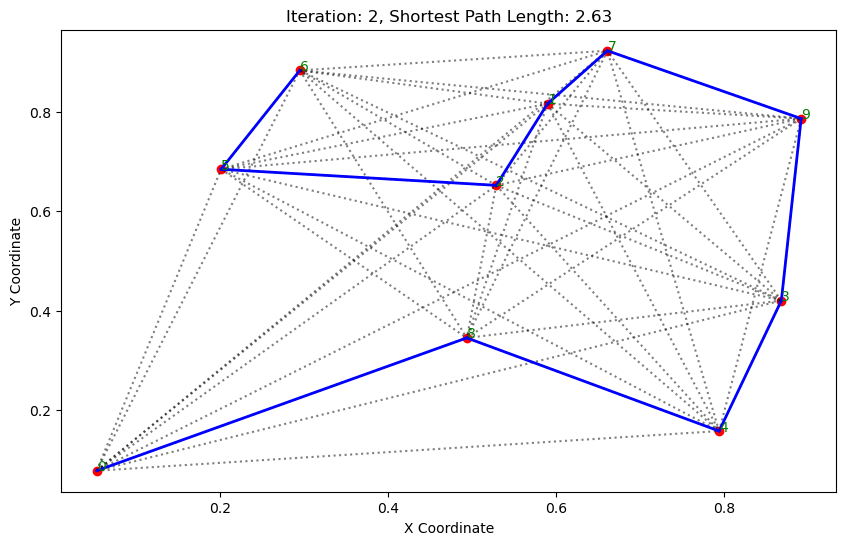
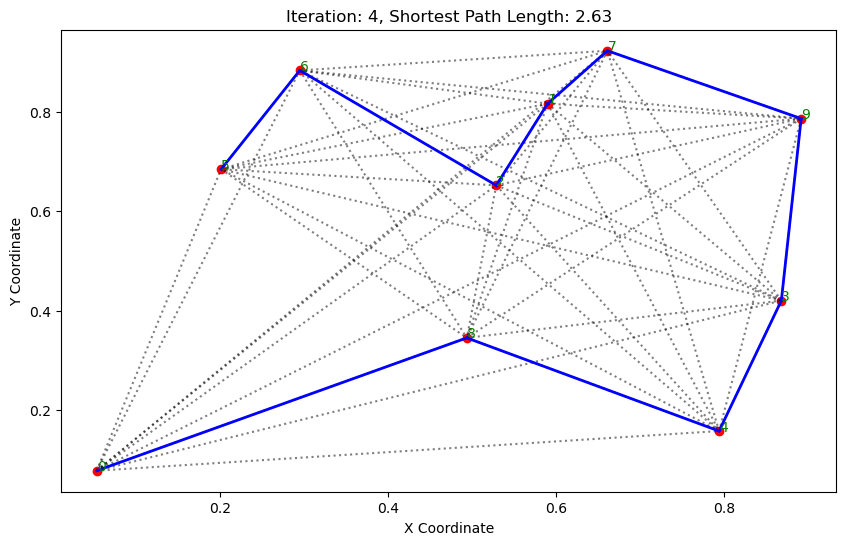
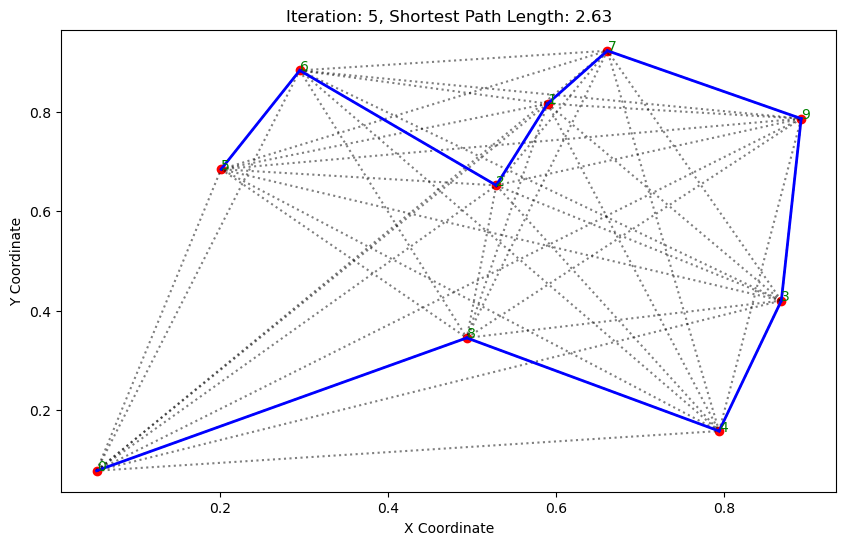
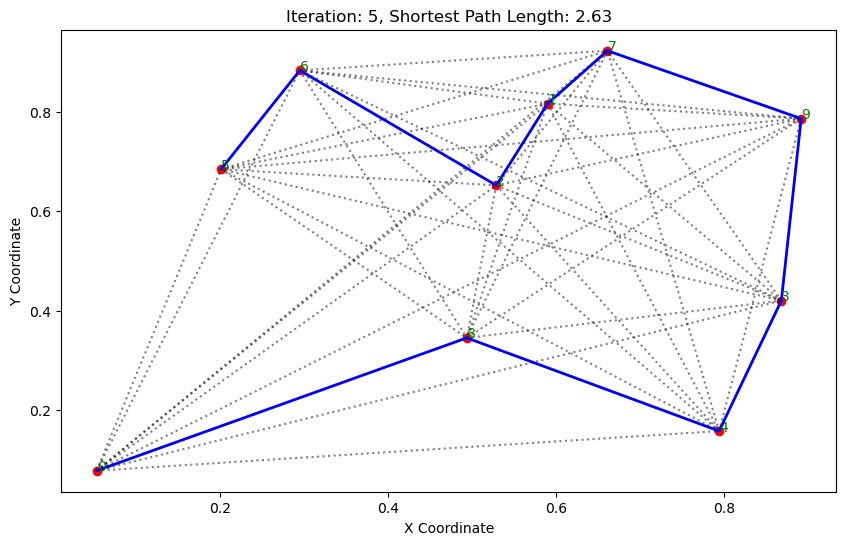
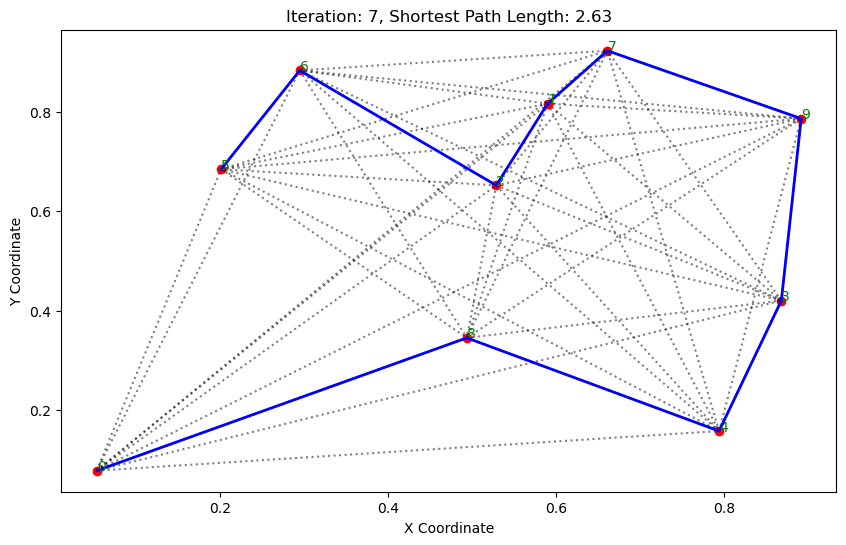
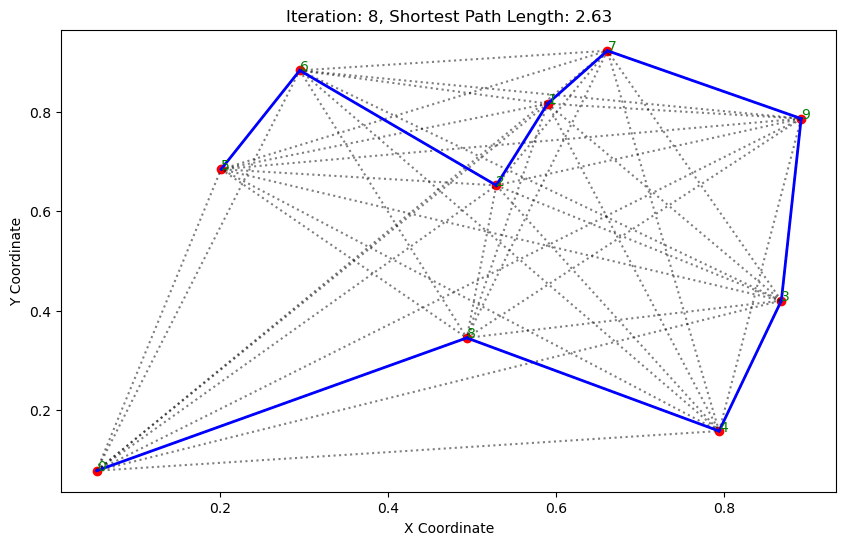
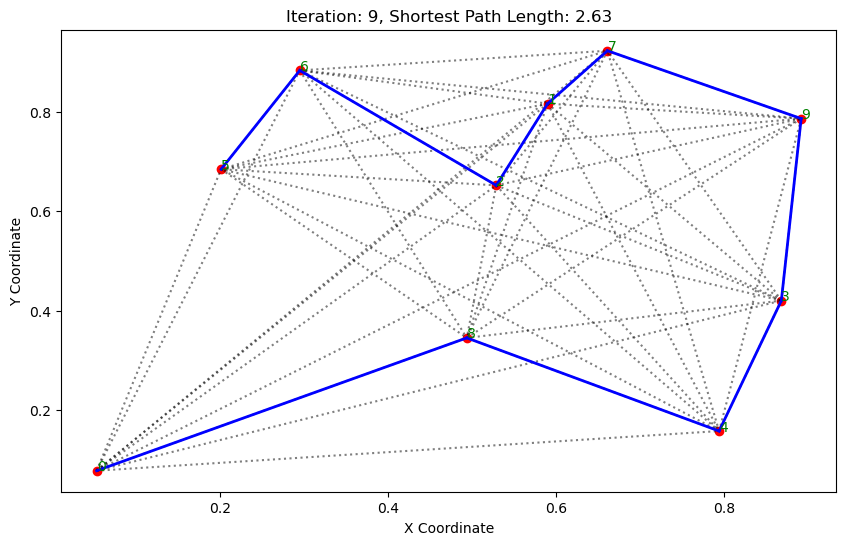
import matplotlib.pyplot as pltclass AntColonyOptimizer:def __init__(self, distances, n_ants, n_best, n_iterations, decay, alpha=1, beta=1):# 初始化参数self.distances = distances # 城市间的距离矩阵self.pheromone = np.ones(self.distances.shape) / len(distances) # 初始化信息素矩阵self.all_inds = range(len(distances)) # 所有城市的索引self.n_ants = n_ants # 蚂蚁数量self.n_best = n_best # 每轮保留的最佳路径数self.n_iterations = n_iterations # 迭代次数self.decay = decay # 信息素的挥发率self.alpha = alpha # 信息素重要程度self.beta = beta # 启发因子的重要程度def run(self):# 运行算法shortest_path = Noneshortest_path_length = float('inf')for iteration in range(self.n_iterations): # 对每次迭代all_paths = self.gen_all_paths() # 生成所有蚂蚁的路径self.spread_pheromone(all_paths, self.n_best, shortest_path_length) # 更新信息素shortest_path, shortest_path_length = self.find_shortest_path(all_paths) # 找到最短路径self.plot_paths(shortest_path, iteration, shortest_path_length) # 绘制路径return shortest_path, shortest_path_lengthdef gen_path_dist(self, path):# 计算路径长度total_dist = 0for i in range(len(path) - 1):total_dist += self.distances[path[i], path[i+1]]return total_distdef gen_all_paths(self):# 生成所有蚂蚁的路径all_paths = []for _ in range(self.n_ants):path = [np.random.randint(len(self.distances))] # 选择一个随机起点while len(path) < len(self.distances):move_probs = self.gen_move_probs(path) # 生成移动概率next_city = np_choice(self.all_inds, 1, p=move_probs)[0] # 选择下一个城市path.append(next_city)all_paths.append((path, self.gen_path_dist(path))) # 添加路径和长度return all_pathsdef spread_pheromone(self, all_paths, n_best, shortest_path_length):# 更新信息素sorted_paths = sorted(all_paths, key=lambda x: x[1]) # 按路径长度排序for path, dist in sorted_paths[:n_best]: # 只取最好的n_best条路径for i in range(len(path) - 1):self.pheromone[path[i], path[i+1]] += 1.0 / self.distances[path[i], path[i+1]]def find_shortest_path(self, all_paths):# 寻找最短路径shortest_path = min(all_paths, key=lambda x: x[1]) # 根据路径长度找到最短的那条return shortest_path[0], shortest_path[1]def gen_move_probs(self, path):# 生成移动概率last_city = path[-1]probs = np.zeros(len(self.distances))for i in self.all_inds:if i not in path:pheromone = self.pheromone[last_city, i] ** self.alphaheuristic = (1.0 / self.distances[last_city, i]) ** self.betaprobs[i] = pheromone * heuristicreturn probs / probs.sum()def plot_paths(self, best_path, iteration, path_length):# 绘制路径plt.figure(figsize=(10, 6))for i in range(len(coords)): # 绘制所有可能的路径for j in range(i+1, len(coords)):plt.plot([coords[i][0], coords[j][0]], [coords[i][1], coords[j][1]], 'k:', alpha=0.5)for i in range(len(best_path) - 1): # 绘制最短路径start_city = best_path[i]end_city = best_path[i+1]plt.plot([coords[start_city][0], coords[end_city][0]], [coords[start_city][1], coords[end_city][1]], 'b-', linewidth=2)plt.scatter(*zip(*coords), color='red') # 标记城市位置for i, coord in enumerate(coords): # 添加城市标签plt.text(coord[0], coord[1], str(i), color='green')plt.title(f'Iteration: {iteration}, Shortest Path Length: {round(path_length, 2)}')plt.xlabel('X Coordinate')plt.ylabel('Y Coordinate')plt.show()def np_choice(a, size, replace=True, p=None):# numpy的随机选择函数return np.array(np.random.choice(a, size=size, replace=replace, p=p))# 城市坐标
coords = np.random.rand(10, 2) # 假设有10个城市# 计算距离矩阵
distances = np.zeros((10, 10))
for i in range(10):for j in range(10):distances[i, j] = np.linalg.norm(coords[i] - coords[j]) # 使用欧几里得距离# 运行蚁群算法
aco = AntColonyOptimizer(distances, n_ants=10, n_best=5, n_iterations=100, decay=0.5, alpha=1, beta=2)
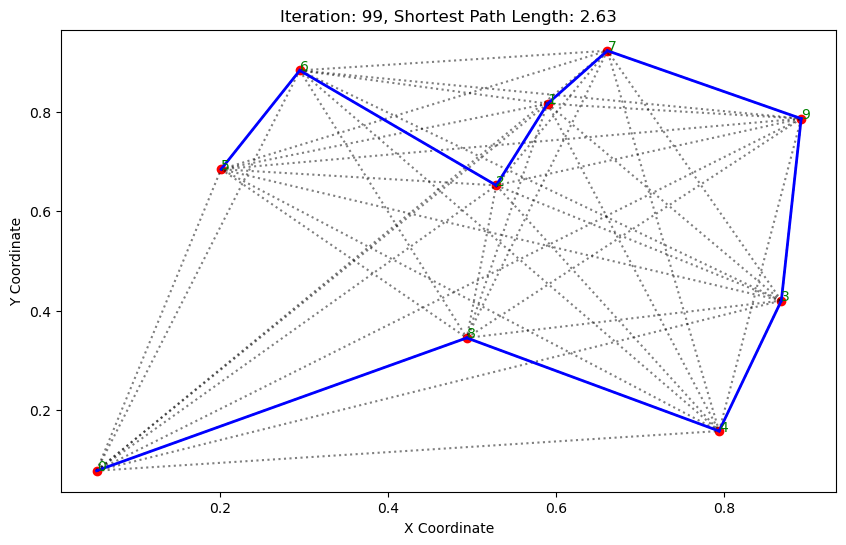
path, dist = aco.run()执行结果:


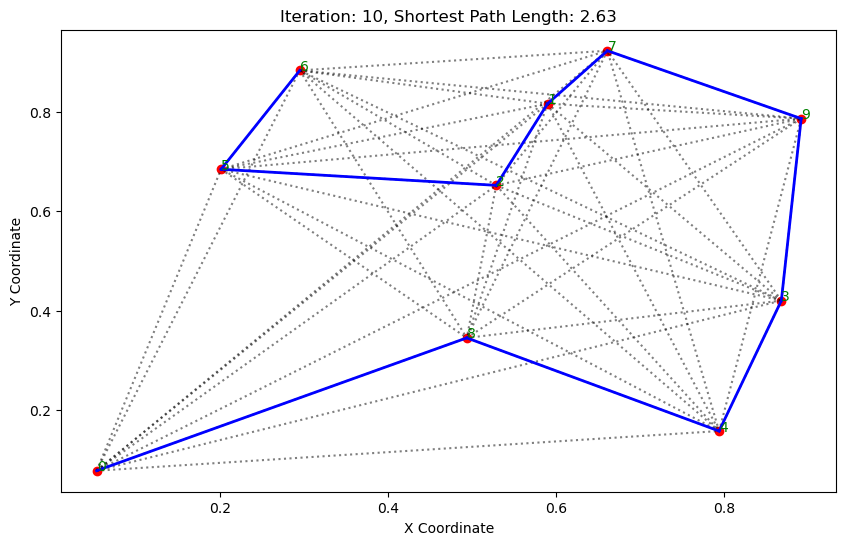
. . . . . . ...... ......
相关文章:

高级人工智能之群体智能:蚁群算法
群体智能 鸟群: 鱼群: 1.基本介绍 蚁群算法(Ant Colony Optimization, ACO)是一种模拟自然界蚂蚁觅食行为的优化算法。它通常用于解决路径优化问题,如旅行商问题(TSP)。 蚁群算法的基本步骤…...

【SpringBoot应用篇】【AOP+注解】SpringBoot+SpEL表达式基于注解实现权限控制
【SpringBoot应用篇】【AOP注解】SpringBootSpEL表达式基于注解实现权限控制 Spring SpEL基本表达式类相关表达式表达式模板 SpEL表达式实现权限控制PreAuthAuthFunPreAuthAspectUserControllerSpelParserUtils Spring SpEL Spring 表达式语言 SpEL 是一种非常强大的表达式语言…...
Java研学-HTTP 协议
一 概述 1 概念和作用 概念:HTTP 是 HyperText Transfer Protocol (超文本传输协议)的简写,它是 TCP/IP 协议之上的一个应用层协议。简单理解就是 HTTP 协议底层是对 TCP/IP 协议的封装。 作用:用于规定浏览器和服务器之间数据传输的格式…...

差生文具多之(二): perf
栈回溯和符号解析是使用 perf 的两大阻力,本文以应用程序 fio 的观测为例子,提供一些处理它们的经验法则,希望帮助大家无痛使用 perf。 前言 系统级性能优化通常包括两个阶段:性能剖析和代码优化: 性能剖析的目标是寻…...

【SPI和API有什么区别】
✅什么是SPI,和API有什么区别 ✅典型解析🟢拓展知识仓🟢如何定义一个SPI🟢SPI的实现原理 ✅SPI的应用场景SpringDubbo ✅典型解析 Java 中区分 API和 SPI,通俗的进: API和 SPI 都是相对的概念,他们的差别只…...
Day67力扣打卡
打卡记录 美丽塔 II(前缀和 单调栈) 链接 class Solution:def maximumSumOfHeights(self, maxHeights: List[int]) -> int:n len(maxHeights)stack collections.deque()pre, suf [0] * n, [0] * nfor i in range(n):while stack and maxHeights…...

什么是网站监控?
网站监控是跟踪网站的可用性和性能,以最小化宕机时间,优化性能并确保顺畅的用户体验。维护网站正常运行对于任何企业来说都是至关重要的,因而对大多数业务来说,网站应用监控都是一个严峻的挑战。Applications Manager网站应用监控…...
游戏软件提示d3dcompiler_43.dll的五个解决方法,亲测靠谱
在使用电脑进行工作,玩游戏的时候,我们常常会遇到一些错误提示,其中之一就是“D3DCompiler_43.dll丢失”的提示。D3DCompiler_43.dll是一个非常重要的动态链接库文件。它是由DirectX SDK提供的,用于编译和优化DirectX着色器代码的…...
python使用opencv提取视频中的每一帧、最后一帧,并存储成图片
提取视频每一帧存储图片 最近在搞视频检测问题,在用到将视频分帧保存为图片时,图片可以保存,但是会出现(-215:Assertion failed) !_img.empty() in function cv::imwrite问题而不能正常运行,在检查代码、检查路径等措施均无果后&…...

说说对React refs 的理解?应用场景?
先了解,是什么? React 中的 Refs提供了一种方式,允许我们访问 DOM节点或在 render方法中创建的 React元素。 本质为ReactDOM.render()返回的组件实例,如果是渲染组件则返回的是组件实例,如果渲染dom则返回的是具体的do…...

Pytorch 读取t7文件
Pytorch 1.0以上可以使用: import torchfileth_path r"./path/xx.t7" data torchfile.load(th_path)print(data.shape)若data的尺寸为0,则将torch版本降为0.4.1,并使用以下函数: from torch.utils.serialization im…...

【YOLOV8预测篇】使用Ultralytics YOLO进行检测、分割、姿态估计和分类实践
目录 一 安装Ultralytics 二 使用预训练的YOLOv8n检测模型 三 使用预训练的YOLOv8n-seg分割模型 四 使用预训练的YOLOv8n-pose姿态模型 五 使用预训练的YOLOv8n-cls分类模型 <...

[Linux] MySQL数据库之索引
一、索引的相关知识 1.1 索引的简介 索引是一个排序列表,包含索引值和包含该值的数据行的物理地址(类似于 c 语言链表,通过指针指向数据记录的内存地址)。 使用索引后可以不用扫描全表来定位某行的数据,而是先通过索…...

【期末考试】计算机网络、网络及其计算 考试重点
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 计算机网络及其计算 期末考点 🚀数…...

力扣labuladong——一刷day79
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣785. 判断二分图二、力扣886. 可能的二分法 前言 给你一幅「图」,请你用两种颜色将图中的所有顶点着色,且使得任意一条边的两个…...

【数据结构入门精讲 | 第十篇】考研408排序算法专项练习(二)
在上文中我们进行了排序算法的判断题、选择题的专项练习,在这一篇中我们将进行排序算法中编程题的练习。 目录 编程题R7-1 字符串的冒泡排序R7-1 抢红包R7-1 PAT排名汇总R7-2 统计工龄R7-1 插入排序还是堆排序R7-2 龙龙送外卖R7-3 家谱处理 编程题 R7-1 字符串的冒…...

【ES实战】Elasticsearch6开始的CCR
【ES实战】学习使用Elasticsearch6开始的CCR 本文涉及官网文章地址 OverviewRequirements for leader indicesAutomatically following indicesGetting started with cross-cluster replicationUpgrading clusters CCR > Cross-cluster replication 文章目录 【ES实战】学…...
Deployment Pay
axure watermark...

MySQL创建member表失败
最近在做一个项目,在台式机上可以跑通,也测试了各个已完成的接口,提交到了GitHub后想着用宿舍的电脑跑一下,在测试member表相关接口时就出错了。报了SQL语法错误,但SQL语句很简单,就根据手机号查询不至于出…...
使用minio实现大文件断点续传
部署 minio 拉取镜像 docker pull minio/minio docker images新建映射目录 新建下面图片里的俩个目录 data(存放对象-实际的数据) config 存放配置开放对应端口 我使用的是腾讯服务器所以 在腾讯的安全页面开启 9000,9090 两个端口就可以了(根据大家实际…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
