数值分析期末复习
第一章 科学计算
误差
解题步骤
x : 真实值 x:真实值 x:真实值 x ∗ : 近似值 x^*:近似值 x∗:近似值
- 先求绝对误差 e ∗ e^* e∗:
x − x ∗ x - x^* x−x∗
绝对误差限是 ∣ x − x ∗ ∣ ≤ ε |x - x^{*}| \le \varepsilon ∣x−x∗∣≤ε
- 求相对误差限:
∣ x − x ∗ ∣ x ∗ \frac{|x\,\,-\,\,x^*|}{x^*} x∗∣x−x∗∣ - 求有效数字
- 先计算 m
- 将绝对误差小于这一个数的半个单位,右上角的阶数为 m-n
- 通过计算得出 n 的值就是有效数字

举个例子:
相减得出结果为0.0000345则小于0.0005,则有效数字为4
例题1:

第二章 线性代数直接法
高斯消去法
高斯顺序消去法解题步骤
(假设是一个三行三列的矩阵):
- 先用第一行消去2,3行
- 再用第二行消去第三行
例题1:

例题2:

高斯列主元消去法解题步骤
- 比较哪一行的绝对值最大,然后交换
- 用第一行消去第2、3行
- 再次比较哪一行绝对值最大,交换
- 重复步骤
例题1:

例题2:


LU分解
LU分解又称为:杜利特尔 (Doolittle)分解法,直接三角分解法
解题步骤
- 将A矩阵分解成L、U矩阵
- L矩阵:下三角矩阵,对角线全为1,其他元素为x
- U矩阵:上三角矩阵,第一行元素和A矩阵相同,其他元素为x
- 从A中矩阵逆向推导,L、U剩下的元素逐一相乘得出结果
- 按照顺序一行一行的元素去算
例题1:



追赶法
追赶法又称为:克劳特分解
解题步骤
- 将A矩阵分解为L、U矩阵
- L矩阵的特点:下三角矩阵,对角线为未知数 α \alpha α,其他元素对A照抄
- U矩阵的特点:上三角矩阵,对角线为1,对角线上面的元素为 β \beta β
- 把 α , β \alpha,\beta α,β全部算出来
- L y = b Ly=b Ly=b -> U x = y Ux=y Ux=y
例题:



第三章 线性代数方程组的迭代法
范数和条件数
- 1范数(列范数):每一列元素的绝对值之和的最大值 ∣ ∣ A ∣ ∣ 1 ||A||_1 ∣∣A∣∣1
- 无穷范数(行范数):每一行元素的绝对值之和的最大值
- 2范数:
- 向量:向量元素平方的和的平方根
- 矩阵(又称为谱范数):null
- 无穷范数条件数:
c o n d ∞ ( A ) = ∣ ∣ A ∣ ∣ ∞ ∣ ∣ A − 1 ∣ ∣ ∞ cond_{\infty}\left( A \right) \,\,=\,\,||A||_{\infty}||A^{-1}||_{\infty} cond∞(A)=∣∣A∣∣∞∣∣A−1∣∣∞
例题1:

例题2:

求 A − 1 A^{-1} A−1的方法
- 初等变换法

雅可比迭代法
解题步骤
- 整体思路:将 Ax=b ->x=Bx+g 的形式
- 先将第一行转换为 x 1 = . . . x_1=... x1=...
- 第二行 x 3 = . . . . x_{3}= .... x3=....
- 以此类推
- 画出表格

计算器解题步骤
- 先将A、B、C、D、E、F设置为0 ( A 代表 x 1 , B 代表 x 2 , C 代表 x 3 A代表x_1,B代表x_2,C代表x_3 A代表x1,B代表x2,C代表x3)
- 0 sto A
- 0 sto B
- 0 sto C
- 0 sto D
- 0 sto E
- 0 sto F
- 将每一行公式输入到计算器中,使用 : : :进行分割
- D = …:E = …:F = …:A=D:B=E:C=F
- 这里是因为一开始不迭代,所以要设置DEF
- D = …:E = …:F = …:A=D:B=E:C=F
高斯迭代法
解题步骤
- 与雅可比迭代类似
- 但是每次都会迭代前面那个值
计算器解题步骤
- 先将A、B、C设置为0 ( A 代表 x 1 , B 代表 x 2 , C 代表 x 3 A代表x_1,B代表x_2,C代表x_3 A代表x1,B代表x2,C代表x3)
- 0 sto A
- 0 sto B
- 0 sto C
- 将每一行公式输入到计算器中,使用 : : :进行分割
- A = …:B = …:C = …
雅可比、高斯敛散性
1. 是否严格对角占优
严格对角占优:每一个对角元素的绝对值都大于它这一行的非对角元素绝对值之和,就是严格对角占优
2. 判断谱半径是否小于 1
- 计算 A 矩阵的L、D、U
A:

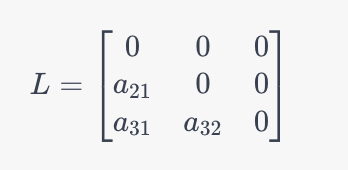
L: 下三角矩阵 L 包含 A 对角线以下的元素,其余位置为 0 (包括对角线)。 下三角矩阵 L 包含 A 对角线以下的元素,其余位置为0(包括对角线)。 下三角矩阵L包含A对角线以下的元素,其余位置为0(包括对角线)。
D: 对角矩阵 D 仅包含 A 的对角线元素,其余位置为 0 。 D − 1 是 D 每个元素的倒数 对角矩阵 D 仅包含 A 的对角线元素,其余位置为0。D^{-1}是D 每个元素的倒数 对角矩阵D仅包含A的对角线元素,其余位置为0。D−1是D每个元素的倒数
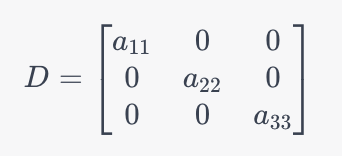
U: 上三角矩阵 U 包含 A 对角线以上的元素,其余位置为 0 (包括对角线)。 上三角矩阵 U 包含 A 对角线以上的元素,其余位置为0(包括对角线)。 上三角矩阵U包含A对角线以上的元素,其余位置为0(包括对角线)。
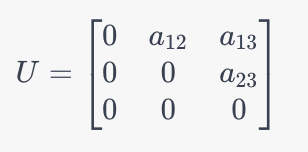
- 计算迭代矩阵 T J = − D − 1 ( L + U ) 计算迭代矩阵 T_J=-D^{-1}(L+U) 计算迭代矩阵TJ=−D−1(L+U)
- 计算出谱半径:特征值绝对值的最大值 如果小于1 则收敛否则不收敛
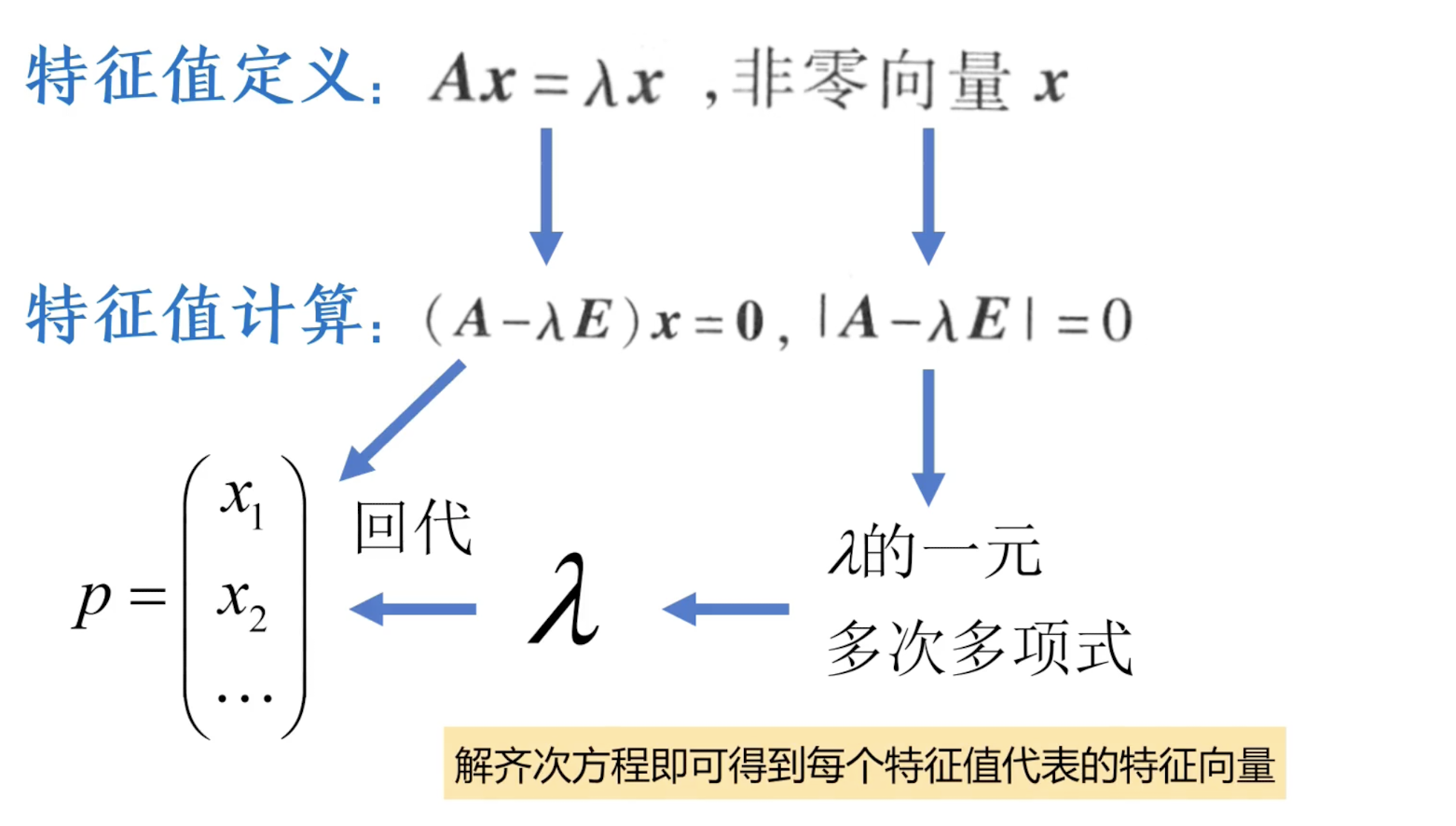
用计算器计算特征值
-
特征值回顾:
-
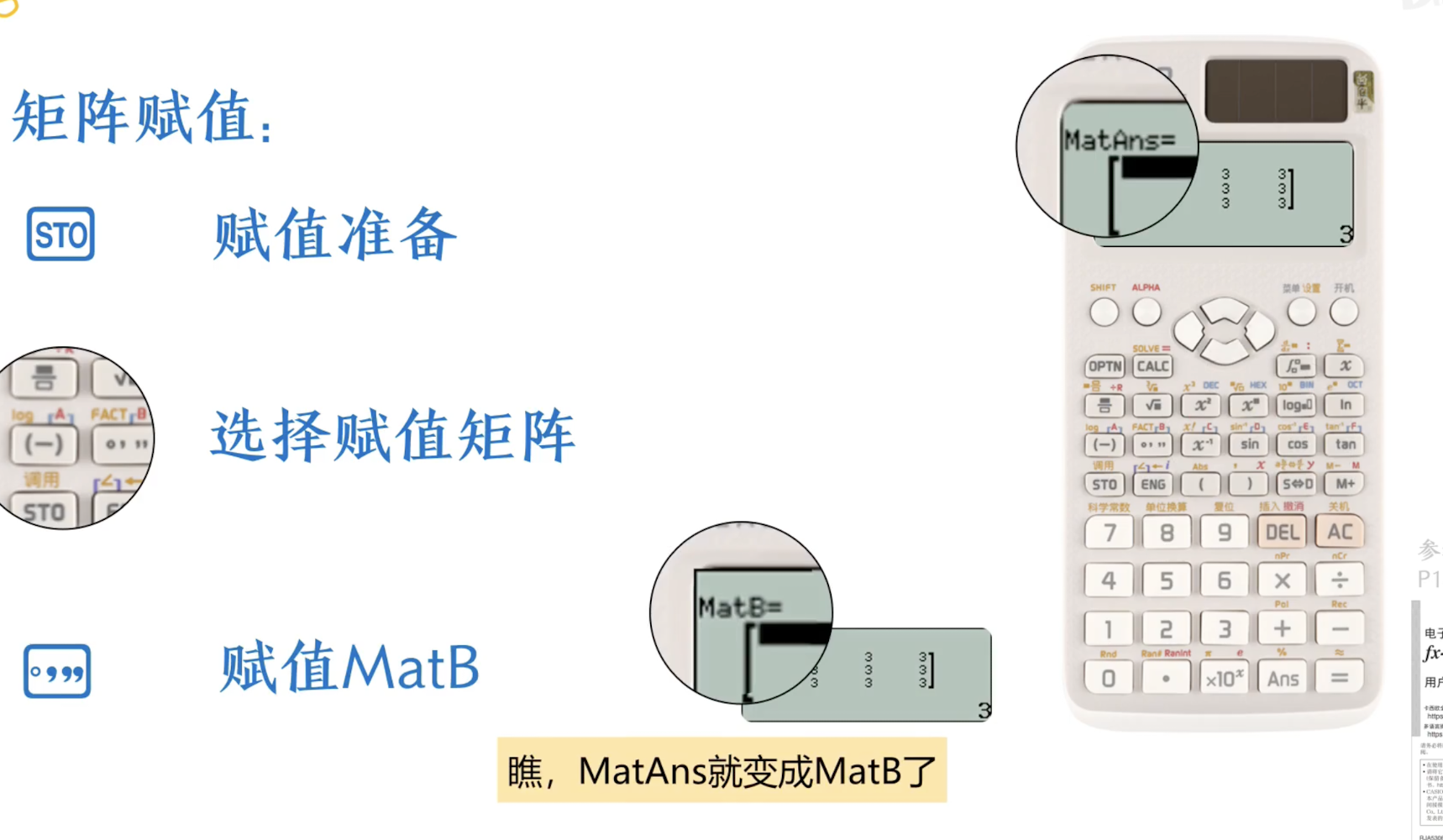
矩阵赋值 将 ANS 赋值给 B
-
∣ A − λ E ∣ = 0 ,算出 λ 1 、 λ 2 、 λ 3 |A-\lambda E| = 0 , 算出 \lambda_{1} 、 \lambda_{2} 、\lambda_3 ∣A−λE∣=0,算出λ1、λ2、λ3
-
再计算出 ( A − λ E ) = 0 (A-\lambda E) = 0 (A−λE)=0
- 化到最简 ( A − λ E ) (A-\lambda E) (A−λE)
第四章 多项式插值和样条插值
拉格朗日插值
一共 2 个部分:
- 插值多项式
- 插值余项
插值多项式
- l n ( x ) = [ ∏ i = 0 , i ≠ j n x − x i x j − x i ] y i l_n(x) =[ \prod_{i=0,i\ne j}^{n}\frac{x-x_i}{x_j-xi}] y_i ln(x)=[∏i=0,i=jnxj−xix−xi]yi
- L n ( x ) = ∑ j = 0 n L j ( x ) y j L_n(x)=\sum_{j=0}^{n}L_j(x)y_j Ln(x)=∑j=0nLj(x)yj
线性 n=1,以此类推后面就是 2 次、3 次
插值余项
- ∣ R n ( x ) ∣ = M n + 1 ( n + 1 ) ! ∣ W n + 1 ( x ) ∣ |R_n(x)|=\frac{M_{n+1}}{(n+1)!} |W_{n+1}(x)| ∣Rn(x)∣=(n+1)!Mn+1∣Wn+1(x)∣
- M n + 1 = max a ≤ x ≤ b ∣ f n + 1 ( x ) ∣ M_{n+1} = \max_{a\le x\le b}|f^{n+1}(x)| Mn+1=maxa≤x≤b∣fn+1(x)∣
- W n + 1 ( x ) = ( x − x 0 ) ( x − x 1 ) . . . ( x − x n ) W_{n+1}(x) = (x-x_0)(x-x_1)...(x-x_n) Wn+1(x)=(x−x0)(x−x1)...(x−xn)
牛顿插值
插值多项式
- f ( x 0 , . . . , x n ) = f n − f n − 1 x n − x 0 f(x_0,...,x_n) = \frac{f_n - f_{n-1}}{x_n-x_0} f(x0,...,xn)=xn−x0fn−fn−1
解题步骤
- 列差商表
| x | f(x) | 一阶差商 |
|---|---|---|
| x 0 x_0 x0 | f 0 f_0 f0 | |
| x 1 x_1 x1 | f 1 f_1 f1 | f ( x 0 , x 1 ) f(x_0,x_1) f(x0,x1) |
以此类推,有 n 个 x 的值就有多少次 n-1 阶差商
- 最后的结果公式
N n ( x ) = f 0 + f ( x 0 , x 1 ) ( x − x 0 ) + . . . + f ( x 0 , . . . , x n + 1 ) ( x − x 0 ) ( x − x 1 ) . . . ( x − x n ) N_{n}(x)=f_0 + f(x_0,x_1)(x-x_0) +...+f(x_0,...,x_{n+1})(x-x_0)(x-x_1)...(x-x_n) Nn(x)=f0+f(x0,x1)(x−x0)+...+f(x0,...,xn+1)(x−x0)(x−x1)...(x−xn)
牛顿插值余项
需要补充
第五章 函数逼近
最佳平方逼近
解题步骤
- 一般题目会给多项式,将其改写为 y = a + b x + c x 2 + d x 3 + . . . y = a + bx + cx^{2}+ dx^{3}+ ... y=a+bx+cx2+dx3+...,还有区间 [ u , d ] [u,d] [u,d]
- 如果是线性最佳平方逼近 多项式为 y = a + b x y= a+ bx y=a+bx
- 这边 φ 0 = 1 \varphi_{0}= 1 φ0=1代表第一个未知数, φ 1 = x , φ 2 = x 2 , φ 3 = x 3 \varphi_{1}= x,\varphi_{2}= x^{2} ,\varphi_{3}=x^3 φ1=x,φ2=x2,φ3=x3
- 列法方程
- ( ( φ 0 , φ 0 ) ( φ 0 , φ 1 ) ( φ 0 , φ 2 ) ( φ 1 , φ 0 ) ( φ 1 , φ 1 ) ( φ 1 , φ 2 ) ( φ 2 , φ 0 ) ( φ 2 , φ 1 ) ( φ 2 , φ 2 ) ( a b c ) = ( ( f , φ 0 ) ( f , φ 1 ) ( f , φ 2 ) ) \begin{pmatrix}(\varphi_0,\varphi_0) & (\varphi_0,\varphi_1) & (\varphi_0,\varphi_2)\\ (\varphi_1,\varphi_0) & (\varphi_1,\varphi_1) & (\varphi_1,\varphi_2)\\ (\varphi_2,\varphi_0) & (\varphi_2,\varphi_1)&(\varphi_2,\varphi_2\end{pmatrix} \begin{pmatrix}a \\b \\c\end{pmatrix} = \begin{pmatrix}(f,\varphi_0) \\(f,\varphi_1) \\(f,\varphi_2)\end{pmatrix} (φ0,φ0)(φ1,φ0)(φ2,φ0)(φ0,φ1)(φ1,φ1)(φ2,φ1)(φ0,φ2)(φ1,φ2)(φ2,φ2 abc = (f,φ0)(f,φ1)(f,φ2)
- 第一个位置以 φ 0 开始,后面每一行开头都自增,第二个位置从 φ 0 到 φ n 结束 第一个位置以\varphi_0开始,后面每一行开头都自增,第二个位置从\varphi_0到\varphi_n结束 第一个位置以φ0开始,后面每一行开头都自增,第二个位置从φ0到φn结束
- a,b,c 是多项式中的 a,b,c
- f 为 y
- 计算
- ( φ 0 , φ 0 ) (\varphi_0,\varphi_0) (φ0,φ0) => ∫ d u φ 0 ∗ φ 0 d x \int_{d}^{u} \varphi_0 * \varphi_0 dx ∫duφ0∗φ0dx
- ( f , φ 0 ) (f,\varphi_0) (f,φ0) => ∫ d u f ∗ φ 0 d x \int_{d}^{u} f* \varphi_0 dx ∫duf∗φ0dx
- 以此类推
- 算出方程后直接代入计算器解出 a,b,c 的值
最小二乘法
解题步骤:
- 通常使用最小二乘法都会带有 x,y 的表格和一个多项式
- 化简多项式为: φ 0 = 1 , φ 1 = x , φ 2 = x 2 , φ 3 = x 3 和 a , b , c 的形式 \varphi_{0}= 1,\varphi_{1}= x,\varphi_{2}= x^{2} ,\varphi_{3}=x^{3}和 a,b,c 的形式 φ0=1,φ1=x,φ2=x2,φ3=x3和a,b,c的形式
- 列法方程
- 计算前先举个例子:
-
y = a + b x y=a + bx y=a+bx -> 这里 φ 0 = 1 , φ 1 = x \varphi_{0}= 1,\varphi_{1} = x φ0=1,φ1=x
x有 3 个,那么 φ 0 = [ 1 1 1 ] \varphi_{0}= \begin{bmatrix} 1\\1 \\1\end{bmatrix} φ0= 111 ,将 x 代入, φ 1 = [ − 3 − 2 − 1 ] \varphi_{1}= \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} φ1= −3−2−1
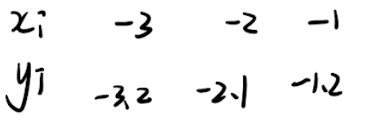
如果有 φ 2 = x 2 \varphi_{2} = x^2 φ2=x2的话,那么 φ 2 = [ ( − 3 ) 2 = 9 ( − 2 ) 2 = 4 ( − 1 ) 2 = 1 ] \varphi_{2} = \begin{bmatrix} (-3)^2 = 9\\(-2) ^ 2 =4 \\ (-1)^2 = 1\end{bmatrix} φ2= (−3)2=9(−2)2=4(−1)2=1
-
建立法方程:
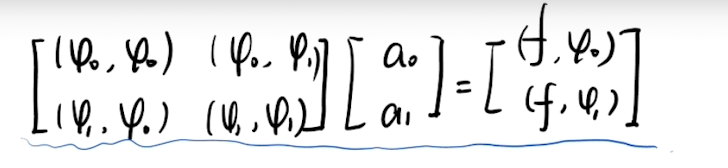
-
( φ 0 , φ 0 ) (\varphi_0,\varphi_0) (φ0,φ0)
- x 个 1 组成的向量内积和 x 个 1 组成的向量内积和 x个1组成的向量内积和
- [ 1 1 1 ] ∗ [ 1 1 1 ] = 1 + 1 + 1 = 3 \begin{bmatrix}1 \\1 \\1\end{bmatrix} * \begin{bmatrix}1 \\1 \\1\end{bmatrix} =1 + 1 + 1 =3 111 ∗ 111 =1+1+1=3
- x 个 1 组成的向量内积和 x 个 1 组成的向量内积和 x个1组成的向量内积和
-
( φ 0 , φ 1 ) (\varphi_0,\varphi_1) (φ0,φ1) = ( φ 1 , φ 0 ) (\varphi_1,\varphi_0) (φ1,φ0) = [ 1 1 1 ] ∗ [ − 3 − 2 − 1 ] = − 3 + ( − 2 ) + ( − 1 ) = − 6 \begin{bmatrix} 1\\1 \\1\end{bmatrix} * \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} = -3 + (-2) + (-1) = -6 111 ∗ −3−2−1 =−3+(−2)+(−1)=−6
-
( φ 1 , φ 1 ) (\varphi_1,\varphi_1) (φ1,φ1) = [ − 3 − 2 − 1 ] ∗ [ − 3 − 2 − 1 ] = 9 + 4 + 1 = 14 \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} * \begin{bmatrix} -3\\-2 \\-1\end{bmatrix} = 9 + 4 + 1 = 14 −3−2−1 ∗ −3−2−1 =9+4+1=14
-
( f , φ 1 ) = [ − 3.2 − 2.1 − 1.2 ] ∗ [ − 3 − 2 − 1 ] = ( − 3 ∗ ( − 3.2 )) + ( − 2.1 ∗ ( − 2 )) + ( − 1.2 + ( − 1 )) = 15 (f,\varphi_1) = \begin{bmatrix} -3.2\\-2.1 \\-1.2\end{bmatrix} * \begin{bmatrix}-3 \\-2 \\-1\end{bmatrix} = (-3*(-3.2)) + (-2.1 * (-2)) + (-1.2 + (-1))=15 (f,φ1)= −3.2−2.1−1.2 ∗ −3−2−1 =(−3∗(−3.2))+(−2.1∗(−2))+(−1.2+(−1))=15
-
-
- 将值代入矩阵,通过计算器得出结果,将 a , b a,b a,b 结果代入 y = a + b x y=a + bx y=a+bx 得到最小二乘拟合函数
第六章 数值积分
尽可能高的代数精度
解题步骤
一般题目会给一个积分 ≈ \approx ≈一个多项式
-
将f(x) 分别计算 1 , x , x 2 , x 3 . . . 1,x,x^2,x^3... 1,x,x2,x3...,取决于多项式中未知数的个数
-
计算出来的值和多项式进行匹配,联立一个方程
-
通过计算器得出结果
-
计算R(f),一般从计算过的x次方的后一个开始计算
- R(f) = 积分 - 多项式
- 如果不等于0 那么精度为次方数m-1
- 等于0 继续算下一个次方


- R(f) = 积分 - 多项式

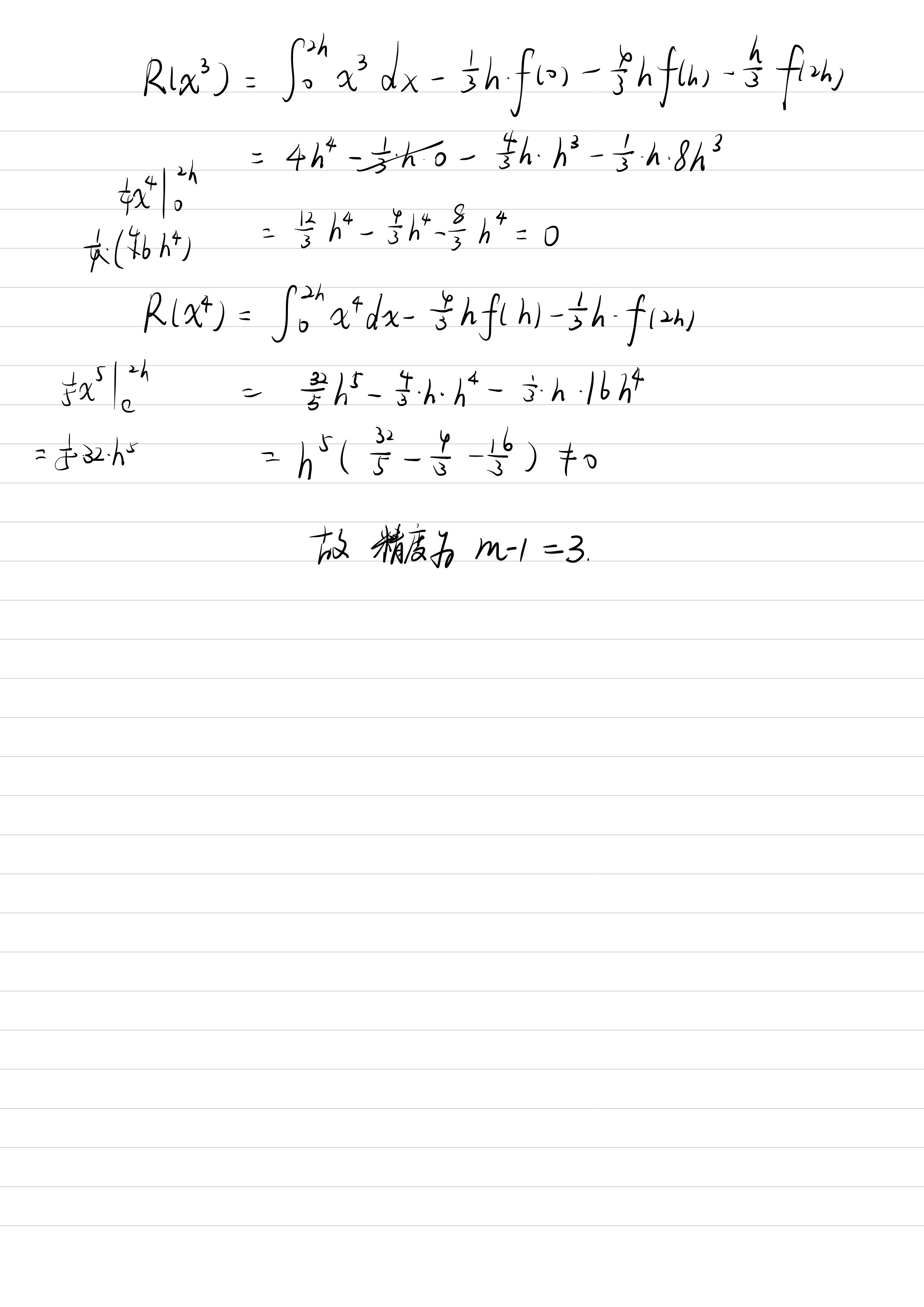
复合梯形公式
解题步骤
-
h = b − a n , n = a , b 区间等分数 h=\frac{b-a}{n},n=a,b\text{区间等分数} h=nb−a,n=a,b区间等分数
-
把所有x的值列出来
-
带入公式
∫ a b f ( x ) d x ≈ h 2 [ f ( a ) + f ( b ) + 2 ∑ k = 1 n − 1 f ( x k ) ] \int_a^b{f\left( x \right) dx\approx \frac{h}{2}\left[ f\left( a \right) +f\left( b \right) +2\sum_{k=1}^{n-1}{f\left( x_k \right)} \right]} ∫abf(x)dx≈2h[f(a)+f(b)+2k=1∑n−1f(xk)] -
计算 ∑ k = 1 n − 1 f ( x k ) \sum_{k=1}^{n-1}{f\left( x_k \right)} ∑k=1n−1f(xk)
- 先得出x的值,举例:
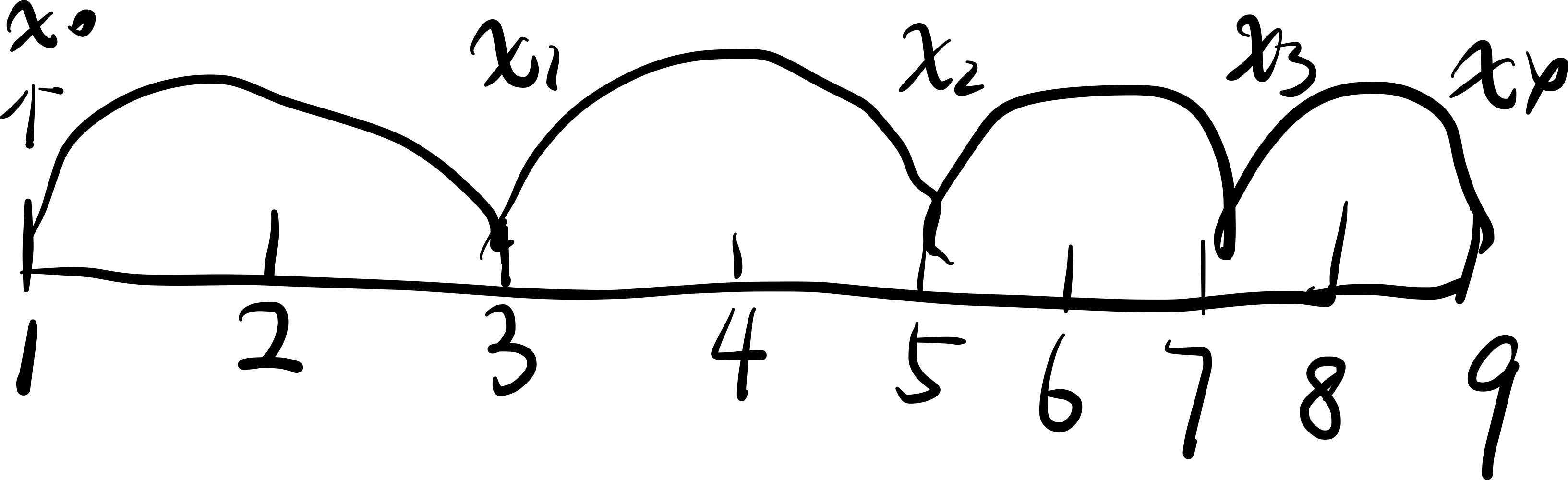
- 带入f函数得出y的值,然后相加
- 先得出x的值,举例:
例题
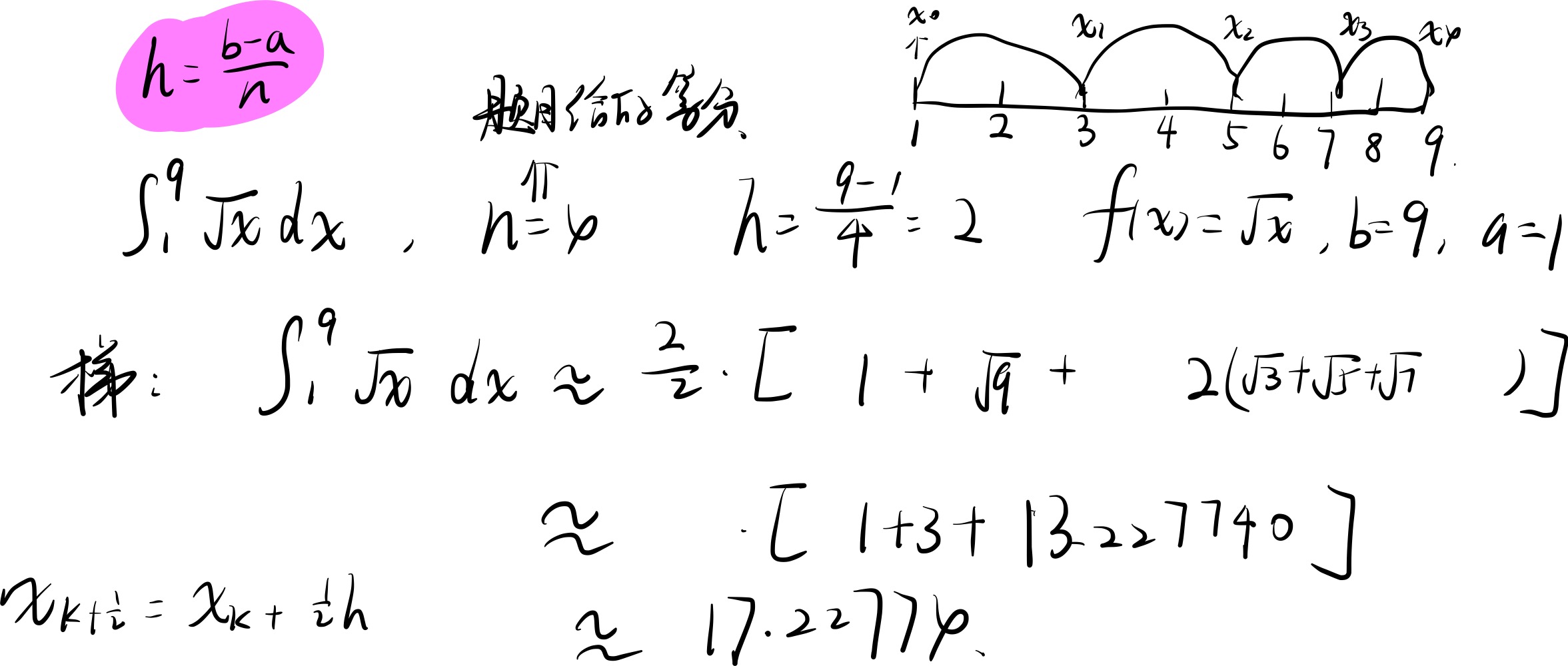
复合辛普森公式
解题步骤
- 前面计算h,n是一样的
- 把所有的x的值列出来
- 计算 x k + 1 2 = x k + h 2 x_{k+\frac{1}{2}}=x_k+\frac{h}{2} xk+21=xk+2h
- 计算公式得出结果:
∫ a b f ( x ) d x ≈ h 6 [ f ( a ) + f ( b ) + 4 ∑ k = 0 n − 1 f ( x k + 1 2 ) + 2 ∑ k = 1 n − 1 f ( x k ) ] \int_a^b{f\left( x \right) dx\approx \frac{h}{6}\left[ f\left( a \right) +f\left( b \right) +4\sum_{k=0}^{n-1}{f\left( x_{k+\frac{1}{2}} \right) +2\sum_{k=1}^{n-1}{f\left( x_k \right)}} \right]} ∫abf(x)dx≈6h[f(a)+f(b)+4k=0∑n−1f(xk+21)+2k=1∑n−1f(xk)]
第九章 常微分方程初边值问题数值解
龙格-库塔公式
基本概念
一般问题会有 y ′ , h , f ( x ) = y y', h , f(x) = y y′,h,f(x)=y等参数
将其转换为
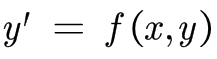
注意h的值,一般是在 0 ≤ x ≤ 1 0 \le x \le 1 0≤x≤1之间,逐渐相加之后递增到1结束计算
四阶四段龙格库塔公式如下:
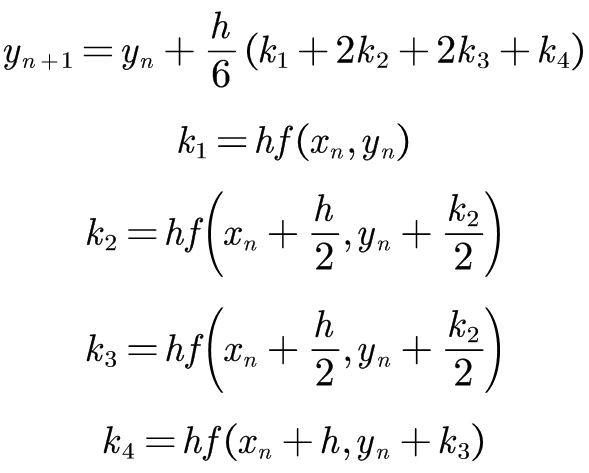
解题步骤
- 将 x 0 , y 0 , h x_0,y_0,h x0,y0,h写在旁边
- 先将题目中给出的已知信息代入 k 1 , k 2 , k 3 , k 4 k_1,k_2,k_3,k_4 k1,k2,k3,k4
- 更新 y n y_n yn的值
- 重复过程
k 2 k_2 k2->f的 x n + h 2 x_n+\frac{h}{2} xn+2h表示 x x x,同理另外一个表示 y y y,将其代入到f(x,y)中进行化简

相关文章:

数值分析期末复习
第一章 科学计算 误差 解题步骤 x : 真实值 x:真实值 x:真实值 x ∗ : 近似值 x^*:近似值 x∗:近似值 先求绝对误差 e ∗ e^* e∗: x − x ∗ x - x^* x−x∗ 绝对误差限是 ∣ x − x ∗ ∣ ≤ ε |x - x^{*}| \le \varepsilon ∣x−x∗∣≤ε 求相对误差限: ∣ x − x ∗…...

k8s的探针
一、探针原理 分布式系统和微服务体系结构的挑战之一是自动检测不正常的应用程序,并将请求(request)重新路由到其他可用系统,恢复损坏的组件。健康检查是应对该挑战的一种可靠方法。使用 Kubernetes,可以通过探针配置运…...

Python 爬虫之下载视频(五)
爬取第三方网站视频 文章目录 爬取第三方网站视频前言一、基本情况二、基本思路三、代码编写四、注意事项(ffmpeg)总结 前言 国内主流的视频平台有点难。。。就暂且记录一些三方视频平台的爬取吧。比如下面这个: 一、基本情况 这次爬取的方…...

Gradle下载地址
Gradle下载地址 Gradle是一个基于JVM的构建工具,是一款通用灵活的构建工具,Gradle也是第一个构建集成工具,与ant、maven、ivy有良好的相容相关性。支持maven, Ivy仓库,支持传递性依赖管理,而不需要远程仓库…...

顺序表的实现(头插、尾插、头删、尾删、查找、删除、插入)
目录 一. 数据结构相关概念 二、线性表 三、顺序表概念及结构 3.1顺序表一般可以分为: 3.2 接口实现: 四、基本操作实现 4.1顺序表初始化 4.2检查空间,如果满了,进行增容编辑 4.3顺序表打印 4.4顺序表销毁 4.5顺…...
VMware虚拟机安装Ubuntu系统教程
所使用的文件如下: VMware Workstation 17 Pro ubuntu-22.04.3-desktop-amd64.iso 一、ubuntu 命名规则及各版本一览表 1.ubuntu 命名规则: 例如:ubuntu 16.04 LTS 是长期维护版本;ubuntu 17.04 是新特性版本 前两位数字为发…...
41 sysfs 文件系统
前言 在 linux 中常见的文件系统 有很多, 如下 基于磁盘的文件系统, ext2, ext3, ext4, xfs, btrfs, jfs, ntfs 内存文件系统, procfs, sysfs, tmpfs, squashfs, debugfs 闪存文件系统, ubifs, jffs2, yaffs 文件系统这一套体系在 linux 有一层 vfs 抽象, 用户程序不用…...

C++面试宝典第9题:找出第K大元素
题目 给定一个整数数组a,同时给定它的大小N和要找的K(1 <= K <= N),请根据快速排序的思路,找出数组中第K大的数(保证答案存在)。比如:数组a为[50, 23, 66, 18, 72],数组大小N为5,K为3,则第K大的数为50。 解析 这道题主要考察应聘者对于快速排序的理解,以及实…...

“马屁精”李白
“李白一斗诗百篇,长安市上酒家眠。天子呼来不上船,自称臣是酒中仙。”这是诗圣杜甫笔下的李白,也是我们脑海里坚信无二的李白。恃才傲物又狂放不羁的诗仙,怎么会低眉顺眼地去拍人马屁呢? 但我要说的是,人…...

python之glob的用法
目录 获取特定扩展名的所有文件 获取特定目录下的所有文件 递归获取所有文件 转义特殊字符 iglob glob 是 Python 中用于文件模式匹配的一个模块。它使用 Unix shell-style 的通配符来进行匹配,并返回所有匹配的文件路径列表。 下面是一些 glob 的基本用法&am…...

【adb】电脑通过ADB向手机传输文件
具体步骤如下: Step1 下载ADB工具 下载最新版本的 ADB工具 !!! 注意:一定要是最新版本的ADB,否则很可能导致无法识别到手机。 将下载的ADB解压以后的文件如下图所示: Step2 添加环境变量 将 ADB的路径 D:\platformtools &…...

npm的常用使用技巧
npm是一个强大的工具,可以帮助你管理Node.js项目中的依赖项。以下是一些有用的npm使用技巧: 使用npm install命令:这个命令可以安装项目的依赖项。如果你想安装一个特定的版本,你可以使用npm install <package><version…...

【网络奇遇记】揭秘计算机网络的性能指标:速率|带宽|吞吐量|时延
🌈个人主页:聆风吟 🔥系列专栏:网络奇遇记、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. 速率1.1 数据量1.2 速率 二. 带宽三. 吞吐量四. 时延4.1 发送时延4.2 传播时延…...

ACM中算法时间约束
ACM中算法时间约束 一般ACM竞赛C/C的时间限制是一秒,因此可以根据题目数据来推断该题所使用的算法。 算法的时间复杂度在 1 0 7 10^7 107左右合适,最多不能超过 1 0 8 10^8 108, O ( n ) O(n) O(n)的极限就在 1 0 8 10^8 108左右。 问题规…...
C++11的列表初始化和右值引用
目录 前言 一、C11的简介 二、C11的小故事。 三、统一的列表初始化 1.列表初始化 2.initializer_list 四、右值引用 1.什么是左值 2.什么是右值 3.右值引用写法 4.右值的分类 5.右值引用的作用 6.STL容器中的右值引用 7.万能引用 总结 前言 C11相较于之C98&…...

千帆起航:探索百度智能云千帆AppBuilder在AI原生应用开发中的革新之路
千帆起航:探索百度千帆AppBuilder在AI原生应用开发中的革新之路 1.揭开帷幕,大模型第二次战役 自从 ChatGPT 横空出世后,一石激起千层浪,人工智能也正在从感知理解走向生成创造,这是一个关键里程碑。生成式大模型完成…...
RevIT™ AAV Enhancer, 提高AAV产量的又一利器!
腺相关病毒 (AAV) 是基因治疗中使用最广泛的传递机制。近年来,基于AAV病毒所开发的基因疗法的研发及临床试验注册数量也呈指数级增长。截止本文撰写之时,美国食品和药物管理局已批准五项AAV疗法,也是全球市场上最为昂贵的药物,其中…...
Kubectl 部署有状态应用(下)
接上文 《Kubectl 部署有状态应用(上)》创建完StatefulSet后,本文继续介绍StatefulSet 扩展、更新、删除等内容。 StatefulSet 中的 Pod 验证序数索引和稳定的网络身份 StatefulSet 中的 Pod 具有唯一的序数索引和稳定的网络身份。 查看 …...

Jmeter 性能 —— 监控服务器!
Jmeter监控Linux需要三个文件 JMeterPlugins-Extras.jar (包:JMeterPlugins-Extras-1.4.0.zip)JMeterPlugins-Standard.jar (包:JMeterPlugins-Standard-1.4.0.zip)ServerAgent-2.2.3.zip 1、Jemter 安装插件 在插件管理中心的搜索Servers Performan…...

离散型制造企业为什么要注重MES管理系统的实施
离散型制造企业经常面临三个核心问题:生产什么、生产多少以及如何生产。尽管许多企业都实施了ERP系统,但仍然绕不开MES管理系统的话题。本文将从三个方面详细解释为什么离散型企业需要实施MES管理系统。 一、生产线经常出现的问题 在离散型企业中&#…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...