【算法学习】斐波那契数列模型-动态规划
前言
我在算法学习过程中,针对斐波那契数列模型的动态规划的例题进行了一个整理,并且根据标准且可靠一点的动态规划解题思路进行求解类似的动归问题,来达到学习和今后复习的必要。
所谓的斐波那契数列模型,即当前状态的值等于前两种状态的值之和。下面的例题的动态规划递推式都是类似的形式。

一、动态规划解题流程
针对于动态规划类似的题目,一般有如下的解题套路:
1.确定状态表示
通常状态我们可以理解为dp表中的每一个值。
此时就跟经验和题目要求相关了。在一维的线性递推模式下(一维数组),一般经验有dp[i]的第i个表示:
1.从第i个开始....
2.到第i个结束...
... 省略的根据题目情况而定,而一般定下的也和我们返回的结果有关。
比如求解上楼梯的方式问题,dp[i]可以表示上第i阶楼梯时有多少种方式(到第i个结束);或者从第i阶楼梯上到顶层楼梯有多少种方式(从第i个开始)。
实际上,也需要我们在分析问题的过程中,发现重复子问题的过程。
2.建立状态转移方程
这一步是核心的一步也是最难的一步。
动态规划基本上解题是基于dp表的,那么对dp表中的状态赋值需要靠建立的转移方程求解。对此一般存在一个基本的思想:dp[i] 的值可以由最近的值如何求解出来?根据题目上的条件。
一般的经验也是以i位置的状态,最近的一步划分问题。
3.初始化
一般状态转移方程中存在让dp表越界的机会,初始化就是为了防止填dp表越界。
基本上完成上面1、2步后,接下来的几步就非常简单了。
4.填表顺序
根据状态转移方程,存在一定的填表顺序,比如斐波那契数列模型,我们每次求当前值时需要知道前面两个值,所以需要从左向右进行赋值。
根据题目和状态定义,灵活的调整填表顺序。
5.返回值
一般返回值就是题目最终要的结果,通常就是返回dp表中的某个状态值。
二、例题1-第n个泰波那契数
在我的上一篇博客中详细提过~
【算法学习】第N个泰波那契数-CSDN博客
三、例题2-三步问题
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
解析题目:
根据动态规划解题思路,我们首先需要确定状态表示。
我们想要求对应台阶小孩有多少种上楼梯的方式,实际上就是经验所谈的到第i结束...。而这里的... 就是题目中的上楼梯的多少种方式,所以这里可以得到状态表示为:
dp[i] = 小孩上第i阶台阶方式总数。
然后我们需要确定状态转移方程。
结合我们之前说过的,从对应值的身边最近状态入手,在结合题目思路就可以得出结果了:因为小孩一次可以上1阶、2阶、3阶。那么dp[i] 此时第i阶台阶可以是通过1阶、2阶、3阶上来的。那么可以存在如下的关系:
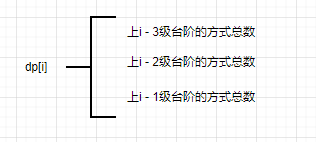
而这实际上对应着如下的关系:
状态转移方程:(i > 3)
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
因为存在三种情况,根据分类计数原理就需要将每种情况进行累加,就可以得到当前状态值的求解了。
其次就需要针对状态转移方程对dp表初始化了(防止越界,比如如果i<3 ,那么i-3<0发生报错)。
对1、2、3的dp值进行赋值即可。为什么不是0、1、2?因为0表示0级台阶,不存在意义,所以我们从1阶开始计算(后续创建dp表注意到开辟空间为n+1)。
1阶对应1种上楼梯方式,2阶对应两种(1步1步上,直接上两步),3阶对应4种(0阶(地面)直接三步上来,1阶两步上来,2阶1步上来)。
填表顺序自然是从左到右,因为我们需要先知道i-1、i-2、i-3的值。
题目要求我们返回对于n阶楼梯,小孩有多少种上楼梯的方式,那么返回值就是对应dp[n]即可。
编码:
编码一般遵循:1.创建dp表2.初始化3.填表的操作。根据上述思路一步一步来即可。
此题注意模的计算。
class Solution {
public:int waysToStep(int n) {if (n < 3) return n;const int M = 1e9 + 7;// 创建dp表vector<int> dp(n + 1);// 初始化dp[1] = 1, dp[2] = 2, dp[3] = 4;// 填表for (int i = 4; i <= n; ++i)dp[i] = ((dp[i - 1] + dp[i - 2]) % M + dp[i - 3]) % M;return dp[n];}
};注意上面只是介绍了基本的dp解题过程,其中对于dp表是存在优化的,可以将空间复杂度On降级为O1。
四、例题3-使用最小花费爬楼梯
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
解析题目:
此题简单描述一下定义不同状态解题的区别。
1.定义状态表示:以i结尾
即dp[i] = 到下标为i的台阶的最低费用。
分析当前状态值如何求解,题目告诉我们在当前i阶花费cost[i]可以向上爬1层或者两层,那么当前i层是之前i-1阶花费钱爬一层或者之前i-2阶花费钱爬两层得到的,即:
状态转移方程:
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
初始化0、1即可。根据题目,可以选择从下标为0和1的台阶开始向上爬,那么dp[0] 和dp[1]都应该为0。
填表顺序从左到右(先需要知道左边的dp状态值)。
题目让我们返回到达楼梯顶部的最低花费,即dp[n];
2.定义状态表示:以i开始
即dp[i] = 从下标为i的台阶开始到楼梯顶部的最低费用。
注意到此时的状态表示发生了变化,那么就近进行分析,因为当前花费cost[i] 我们可以选择爬1层和爬2层,如果爬1层后是最低费用就爬此,否则就爬另外的一个,如此,就有如下的结果:
状态转移方程:
dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i];
此时由于状态表示发生了变化,根据递推方程,初始化的方式也发生了变化,我们需要从后往前进行赋值,可以发现实际上我们可以直接求得dp[n - 1]和dp[n - 2]的值(此时dp[n]=0不存在意义了,到达顶层可以是最后一级台阶花费爬一步,或者倒数第二级台阶花费爬两步),所以初始化dp[n - 1]、dp[n - 2]即可。dp[n - 1] = cost[n - 2], dp[n - 2] = cost[n - 1]。
填表顺序为从右到左,我们需要先知道较大下标的值才能求解较小下标的状态值。
题目让我们返回到达楼梯顶部的最低花费,因为我们可以选择0、或者1开始往上爬,根据dp值只需要两者之间比较较小的花费返回即可:min(dp[0], dp[1]);
可以看到,我们将状态定义的不同,后续步骤方程基本不一样,所以定义状态按照自己习惯或者合适的场景进行理解。
编码:
1.以i结尾
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {// 解法1 设置dp表中的状态表示为到第i台阶花费的最低花费int n = cost.size();// 创建dp表vector<int> dp(n + 1);//初始化dp[0] = dp[1] = 0;// 填表for (int i = 2; i <= n; ++i)dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);return dp[n];}
};2.以i开始
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {// 解法2 设置dp表中的状态表示为从第i台阶开始到顶部的最低花费总和int n = cost.size();// 创建dp表vector<int> dp(n);// 初始化dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2];// 填表for (int i = n - 3; i >= 0; --i)dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i];return min(dp[0], dp[1]);}
};五、例题4-解码方法
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

解析题目:
针对此题,我们可以提出另外的一种优化方式,来优化我们的动态规划编码,使其看的非常整洁。
状态的定义我们就以习惯的以i结尾...:s中以i下标结尾时解码方法的总数。
dp[i] = s中以i下标结尾时解码方法的总数。
对于当前状态值得求解,分析题目,数字可以单独被解码,也可以两个结合解码。
对于一个在s中对应i下标得数字,存在单独解码和结合解码两种思路讨论,那么是和前面结合还是后面结合呢?注意看我们的状态定义:是以i下标结尾时的解码方法总数,不包括后面的解码的,所以是和前面的一个数进行结合解码。

在细分的去划分,存在解码成功和解码失败。单个解码只要大于0解码成功,否则解码失败,结合解码需要大于等于10、小于26解码成功,否则失败(题目要求:06、60类似这种解码失败) 。
如果单独解码成功,那么实际上就是在以i-1解码方法的基础上,后面添加了个字母,失败的话,那么以i结尾的解码方法总数加上0。
例子:i=2
s="112"
i - 1 = 1的解码方法总数:2
1、1 aa
11 k
那么2单解码成功
i此时的解码方法总数为:0+2
1、1、2 aab
11、2 kb
如果结合解码成功,那么实际上就是在i-2解码方法的基础上,后面添加了个字母,失败的话,那么以i结尾的解码方法总数加上0.
例子:i=2
s="112"
i - 2 = 0的解码方法总数:1
1 a
那么2结合解码成功
i此时的解码方法总数为:0+1
1、12 aL
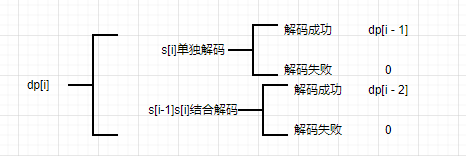
综上,我们可以得到状态转移方程为:
状态转移方程:
dp[i] = (if int(s[i]) > 0: dp[i - 1] else: 0) +
(if 10 <= int(s[i-1] + s[i]) <= 26: dp[i - 2] else :0)
得到状态转移方程后我们需要进行初始化。
需要注意此处的初始化,正常情况下我们需要初始化0、1从而满足dp表不越界的情况,对应的求解dp[1]下标结尾的解码方法总数和状态转移方程有些一样,如果像原本那样写在外面会造成代码存在一定的冗余,我们可以将原本的dp数组扩大一个单位,整体右移。这样多出的一个就可以用来初始化s[1]了。
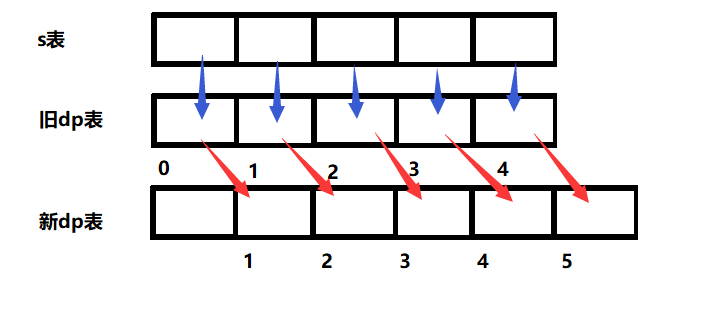
此时新增的第一位称作虚拟位,一般虚拟位的值为0(一般情况下,要结合实际情况,此题情况就不为0).这样就可以将旧dp[1]繁琐的步骤进行优化。
根据图示,需要注意的是:
1.虚拟节点内的值,需要保证后续的填表是正确的。(一般情况下是0正确的,但是在此题是错误的,要填1 -分析)
2.注意下标的映射关系 dp和s对应的关系。
此题需要满足优化后dp[2] 为s下下标为1的解码总数,根据递推公式,如果结合解码成功,需要加上i - 2的dp值,也就是此时对应虚拟节点的对应值,不能给0的原因在这里,给0的话,那么此时结合解码就失效了,所以需要加1,此时虚拟节点的值给予1即可。
填表顺序就是从左到右了,返回值根据是否优化返回dp[n]或者dp[n-1]表示此串s编码的解码方法总数了。
编码:
1.初始化不优化
class Solution {
public:int numDecodings(string s) { int n = s.size();// 建立dp表 状态标识:到第i个编码的解码方法总数vector<int> dp(n);// 初始化dp[0] = s[0] != '0';if (n == 1) return dp[0];if ((s[1] - '0') > 0) dp[1] += dp[0]; int tmp = (s[0] - '0') * 10 + (s[1] - '0');if (tmp >= 10 && tmp <= 26) dp[1] += 1;// 填表 递推公式:第i个可以单独编码 dp[i] += dp[i - 1] 第i个和第i-1个可以凑在一起编码 dp[i] += dp[i - 2]for (int i = 2; i < n; ++i){if (s[i] - '0' > 0) dp[i] += dp[i - 1];tmp = (s[i - 1] - '0') * 10 + s[i] - '0';if (tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];}return dp[n - 1];
};可以看到初始化有点繁琐不简洁,而下面优化后的方案就非常简洁了。
2.初始化优化
class Solution {
public:int numDecodings(string s) { int n = s.size();// 建立dp表 状态标识:到第i个编码的解码方法总数vector<int> dp(n + 1);// 初始化 优化初始化dp[0] = 1;dp[1] = s[0] != '0';if (n == 1) return dp[1];// 填表 递推公式:第i个可以单独编码 dp[i] += dp[i - 1] 第i个和第i-1个可以凑在一起编码 dp[i] += dp[i - 2]for (int i = 2; i <= n; ++i){if (s[i - 1] - '0' > 0) dp[i] += dp[i - 1];int tmp = (s[i - 2] - '0') * 10 + s[i - 1] - '0';if (tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];}return dp[n];}
};相关文章:

【算法学习】斐波那契数列模型-动态规划
前言 我在算法学习过程中,针对斐波那契数列模型的动态规划的例题进行了一个整理,并且根据标准且可靠一点的动态规划解题思路进行求解类似的动归问题,来达到学习和今后复习的必要。 所谓的斐波那契数列模型,即当前状态的值等于前两…...
ES的安装和RestClient的操作
目录 初识elasticsearch 什么是elasticsearch elasticsearch的发展 Lucene的优缺点 elasticsearch的优势 倒排索引 es与mysql的概念对比 文档 索引 概念对比 架构 安装es 安装kibana 安装ik分词器 分词器 安装ik分词器 ik分词器的拓展和停用词典 操作索引库…...
)
访问者模式(Visitor)
访问者模式(Visitor Pattern)是一种将算法与对象结构分离的行为型设计模式。这种模式主要用于对一个由许多不同类型的对象构成的复杂对象结构(如组合结构)进行操作,而不需要对这些对象的类进行修改。 访问者模式涉及以下几个角色: 访问者(Visitor):为每一个具体元素类…...

ATTCK红队评估一
一、环境搭建 主机 ip地址 win7外网服务器(两张网卡) 外网:192.168.92.135 内网:192.168.52.143 server2003域成员主机 内网:192.168.52.141 server2008域空主机 内网:192.168.52.138 kali攻击机 …...
W5500-EVB-Pico评估版介绍
文章目录 1 概述2 板载资源2.1 硬件规格2.2 硬件规格2.3 工作条件 3 参考资料3.2 原理图3.3 尺寸图 (单位 : mm)3.4 参考例程 4 硬件协议栈优势 1 概述 W5500-EVB-Pico是基于树莓派RP2040和完全硬连线TCP/IP控制器W5500的微控制器开发板-基本上与树莓派Pico板相同,但…...
单聊和群聊
TCP协议单聊 服务端: import java.awt.BorderLayout; import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.io.PrintWriter; import java.net.ServerSocket; import java.net.Socket; import java.util.Vec…...

Swift 检测 iCloud状态
Show me the code: func isICloudContainerAvailable() -> Bool {if let _ FileManager.default.ubiquityIdentityToken {return true} else {return false} }推荐一下刚上线的 App 熊猫小账本,里面有用到这篇博客讲的内容 熊猫小账本 一个简洁的记账 App&…...
)
使用Windi CSS(基于vue-cli)
1、先创建vue项目 利用脚手架vue-cli创建,根据需求设置vue版本、babel等,无特别要求直接用默认的vue2或vue3就行 vue create 项目名 2、运行vue项目,利用vue-cli安装Windi CSS 官网指导:Vue CLI 集成 | Windi CSS 我的经历&a…...
操作无法完成(错误 0x000006ba),Windows 11 PDF打印机无法使用解决办法
操作无法完成(错误 0x000006ba),Windows 11 PDF打印机无法使用解决办法 解决方式一 先重启一次电脑,看看是否可以解决问题。 解决方式二 重新启动 Printer Spooler 服务...
Settings中电池选项-Android13
Settings中电池选项-Android13 1、设置中界面2、电池计算2.1 充电时间计算2.1.1 BatteryUsageStats获取2.1.2 BatteryStatsImpl计算 2.2 电池剩余使用时间2.2.1 Estimate获取2.2.2 BatteryStatsImpl计算 3、电池信息来源4、命令模拟* 日志 [电池]Android 9.0 电池未充电与充电字…...

解密 Java ForEach 提前终止问题
目录 前言:场景复现分析与解决方案解决方案详解总结 前言: 你是否曾在使用 Java 8 的 forEach 迭代集合时遇到过提前终止循环的问题?在这篇博客中,我们将深入探讨这一问题,并提供多种解决方案。通过场景复现、分析源码…...

7_js_dom编程入门1
Objective(本课目标) 掌握获取页面元素的常用方法 掌握事件触发案例 能够区分innerText和innerHTML的区别 综合案例训练 1 DOM 介绍 1.1 什么是DOM 文档对象模型(Document Object Model,简称DOM),是 …...
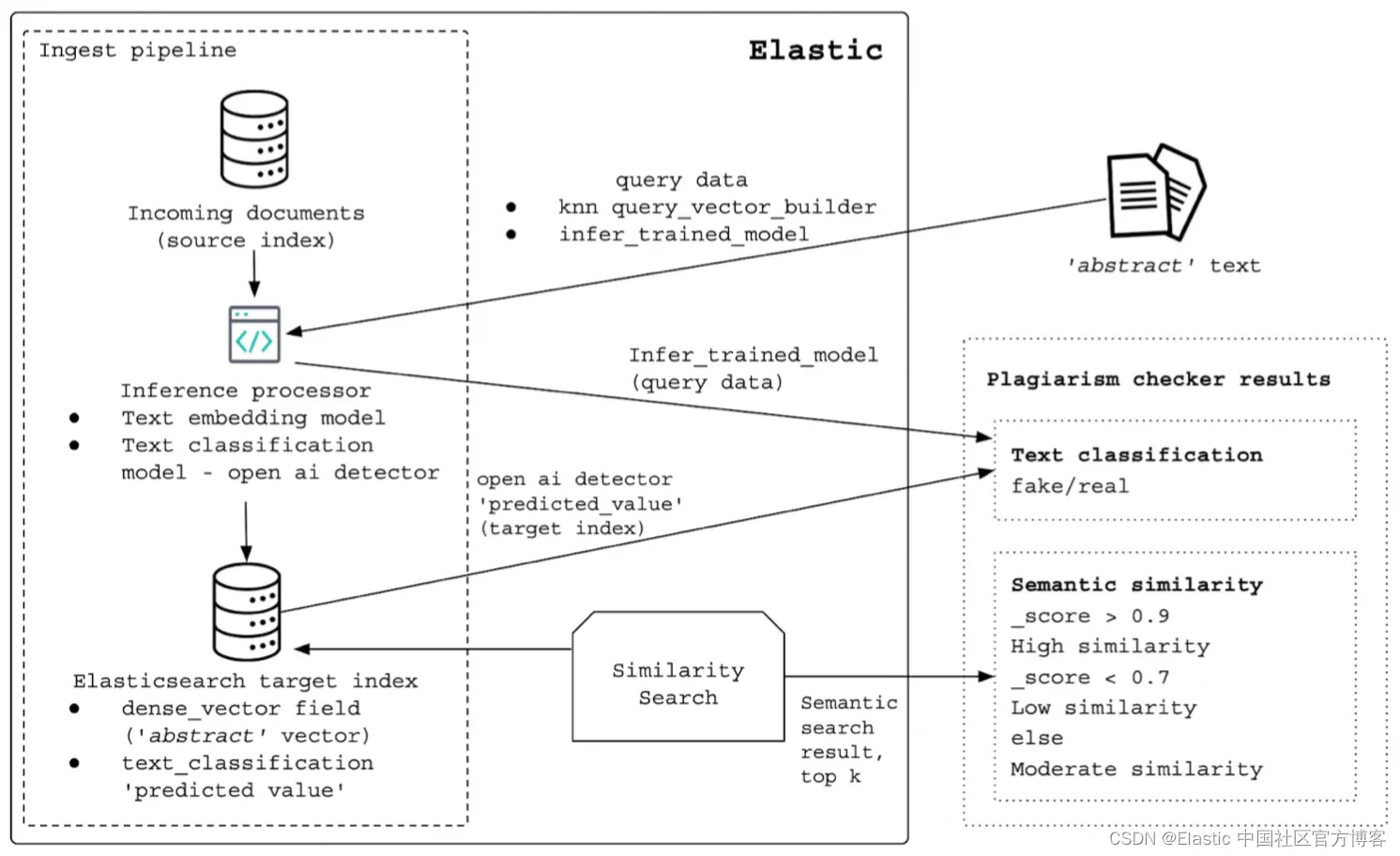
使用 Elasticsearch 检测抄袭 (一)
作者:Priscilla Parodi 抄袭可以是直接的,涉及复制部分或全部内容,也可以是释义的,即通过更改一些单词或短语来重新表述作者的作品。 灵感和释义之间是有区别的。 即使你得出类似的结论,也可以阅读内容,获得…...
STM32 cubeMX 直流电机控制风扇转动
本文使用的是 HAL 库。 文章目录 前言一、直流电机介绍二、直流电机原理图三、直流电机控制方法四、STM32CubeMX 配置直流电机五、代码编写总结 前言 实验开发板:STM32F051K8。所需软件:keil5 , cubeMX 。实验目的:了解 直流电机…...
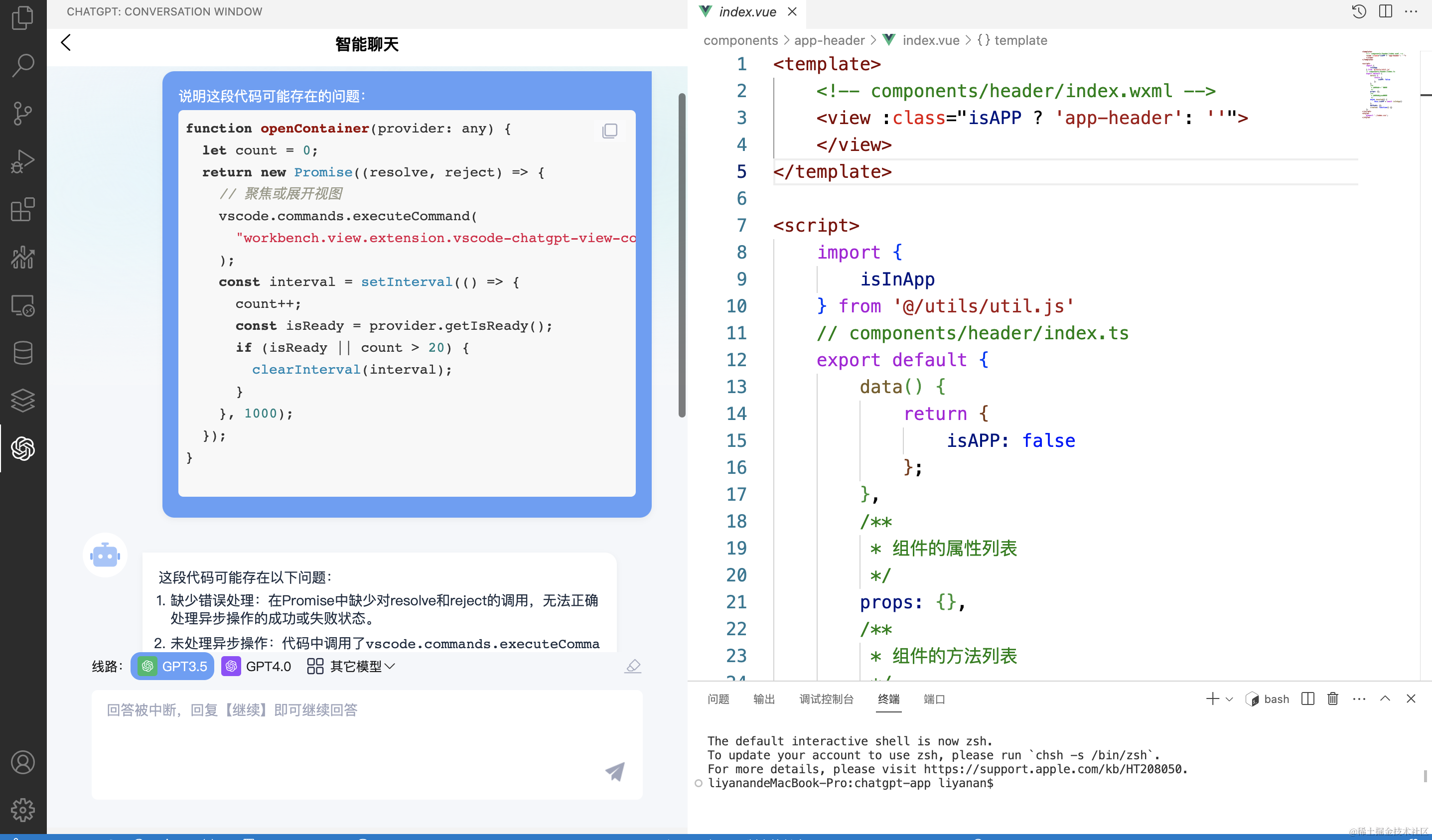
我在 VSCode 插件里接入了 ChatGPT,解决了Bug无法定位的难题
作为一名软件开发者,我时常面临着代码中Bug的定位和解决问题。这个过程往往既费时又充满挑战。然而,最近我在我的VSCode插件中接入了ChatGPT,这个决定彻底改变了我处理Bug的方式。 Bug:开发者的噩梦 在开发过程中,遇…...

学Java的第四天
一、switch语句 switch (表达式) { case 1: 语句体1; break; case 2: 语句体2; break; ... default: 语句体n1; break; } 首先计算表达式的值,然后和case 比较,有对应的值就执行对应的语句,遇到 break 就结束。 最后如果所有的cas…...
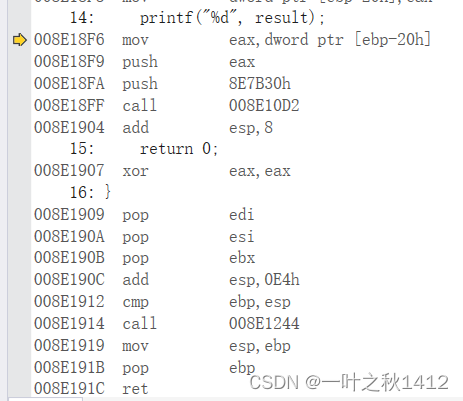
[内功修炼]函数栈帧的创建与销毁
文章目录 1:什么是函数栈帧2:理解函数栈帧能解决什么问题呢3:函数栈帧的创建与销毁的解析3.1:什么是栈3.2:认识相关寄存器与汇编指令相关寄存器相关汇编指令 3.3 解析函数栈帧的创建和销毁3.3.1 预备知识3.3.2 详细解析一:调用main函数,为main函数开辟函数栈帧First:push前push…...
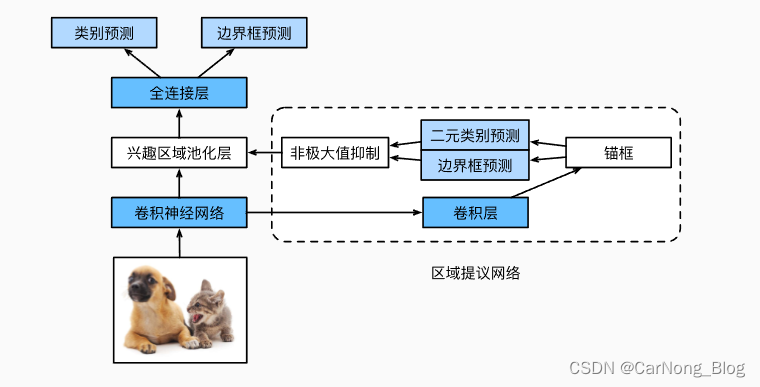
【深度学习-目标检测】03 - Faster R-CNN 论文学习与总结
论文地址:Faster R-CNN: Towards Real-Time ObjectDetection with Region Proposal Networks 论文学习 1. 摘要与引言 研究背景与挑战:当前最先进的目标检测网络依赖于 区域提议(Region Proposals)来假设目标的位置,…...

oracle11体系结构二-存储结构
数据区: 数据区(数据扩展区)由一组连续的oracle数据块所构成的存储结构,一个或多个数据块组成一个数据区,一个或多个数据区组成一个段。当段中所有空间被使用完后,oracle系统将自动为该段分配一个新的数据…...
如何通过内网穿透实现远程访问本地Linux SVN服务
文章目录 前言1. Ubuntu安装SVN服务2. 修改配置文件2.1 修改svnserve.conf文件2.2 修改passwd文件2.3 修改authz文件 3. 启动svn服务4. 内网穿透4.1 安装cpolar内网穿透4.2 创建隧道映射本地端口 5. 测试公网访问6. 配置固定公网TCP端口地址6.1 保留一个固定的公网TCP端口地址6…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...