当前位置： 首页 > news >正文

Best Arm Identification in Batched Multi-armed Bandit Problems

news 2026/2/8 11:53:22

Q: 这篇论文试图解决什么问题？

A: 这篇论文试图解决在批量多臂老虎机问题中进行最佳臂识别（BAI）的挑战，其中必须成批地对臂进行抽样，因为代理等待反馈的时间有限。这种场景出现在许多现实世界的应用中，例如生物实验和在线营销。当臂的数量很大且批次数量很少时，问题变得更加复杂。作者提出了一种通用的线性规划框架，可以并入不同理论设置的最佳臂识别目标。这个线性规划导致了一个两阶段算法，可以实现良好的理论性质。通过数值研究，作者展示了该算法与某些UCB类型或汤普森抽样方法相比也具有良好的性能。

Q: 有哪些相关研究？

A: 这篇论文提到了与批量多臂老虎机和贝叶斯老虎机相关的多项研究。一些相关的研究包括： 1. Even-Dar等人（2002）提出了一个下界，即在（ϵ，δ）-PAC设置下的抽样成本为Ω（K log（1/δ）/ϵ²）。 2. Kalyanakrishnan等人（2012）提出了LUCB算法，用于在（ϵ，δ）-PAC设置下的前k臂推荐问题。 3. Lattimore等人（2016）获得了最小化遗憾的极小遗憾界。 4. W¨uthrich等人（2021）为期望改进和UCB算法的变体建立了遗憾界。 5. Carpentier和Locatelli（2016）展示了在FB和FC设置中，1-PB的基本下界为exp{−T/(H log K)}，其中H = ∑（j = 2）ⁿ(∆²⁻¹)。 6. Perchet等人（2016）针对具有次高斯奖励的两臂老虎机使用了一种探索然后承诺策略，并获得了累积遗憾的上下界。 7. Gao等人（2019）展示了实现最小化遗憾所需的批次数为Ω（log log T），以实现最小化遗憾的最优性。 8. Jun等人（2016）提出了BatchRacing算法，用于FC设置，以及BatchSAR算法，用于FB设置。 9. Agarwal等人（2017）提出了一种积极的消除算法，只需要Θ(log∗K)批次。 10. Komiyama等人（2023）提出了一种两阶段探索算法，并在贝叶斯设置下进行了简单遗憾分析。 这些研究为批量多臂老虎机问题的不同方面提供了见解，例如探索-利用权衡、遗憾最小化和贝叶斯方法。

Q: 论文如何解决这个问题？

A: 为了解决批量多臂老虎机问题中最佳臂识别的挑战，论文提出了以下方法： 1. 引入了一个通用的线性规划框架，可以并入不同理论设置的最佳臂识别目标。这个框架被进一步放松为一个线性规划（LP）框架，可以生成独立于同伴的政策。 2. 在引入的LP框架下，指定了四种不同的设置，即PAC、SRM、FC和FB。PAC和SRM设置特别适用于大K小R的情况。 3. 提出了一个两阶段算法LP2S，具有良好的理论性质和强大的数值性能。该算法的第一阶段是一个同伴无关的过程，由LP诱导，可以通过在各个臂的累积奖励上设置阈值来有效选择好的臂。两阶段算法的期望总抽样成本为O(Lh®)，其中h®最多是R的多项式。作者还为LP的不同变体获得了合理的上限。 总之，论文通过采用更积极的臂消除方案、引入通用的LP框架以及开发具有良好理论和数值性能的两阶段算法来解决批量多臂老虎机问题中最佳臂识别的挑战。

Q: 论文做了哪些实验？

A: 论文进行了三个数值实验来研究LP2S算法的性能。这些实验分别对应于在LP2S的第一阶段应用LP-SRM、LP-PAC和LP-FC。 1. 在第一个实验中，应用了LP-PAC到LP2S的第一阶段。作者假设π = Beta（a，b），其中（a，b）=（1,1），（5,1）或（1,3）。他们设置了K = 1000、2000或5000。对于LP2S，他们取R = c1 log K，L = c2 log K，其中c1 = 30，c2 = 3，µ0 = 0.7对于（a，b）=（1,1）或（1,3），µ0 = 0.8对于（a，b）=（5,1），δ0是使LP可行的最小数字。作者将LP2S与两种竞争方法进行比较：Komiyama等人（2023）的两阶段探索（TSE）和Kalkanli和¨Ozg¨ur（2021）的批量汤普森抽样。他们还在Jun等人（2016）的BatchRacing上进行了实验。他们以两种不同的方式进行比较：首先，将三种竞争方法的总抽样成本设置为与LP2S大致相等，并比较四次模拟运行的平均简单遗憾。其次，将三种竞争方法的简单遗憾设置为与LP2S大致相等，并比较所有方法的平均总抽样成本。结果表明，在相同的抽样成本下，LP2S具有最小的简单遗憾，并且在类似的简单遗憾下具有最小的抽样成本。 2. 在第二个实验中，应用了LP-SRM到LP2S的第一阶段。参数与第一个实验相同，只是不需要指定µ0。作者报告了平均简单遗憾和抽样成本的结果，并得出了与第一个实验相同的结论，即LP2S具有最小的简单遗憾，并且在相同的抽样成本下具有最小的抽样成本。 3. 在最后一个实验中，测试了由LP-FC诱导的LP2S的性能。作者保持与前两个实验相同的先验分布，但只考虑K = 200。这是因为LP-FC要求R ≳ K，但当R变大时，LP变得过于计算昂贵。他们将LP2S的R = 300，L = 5和δ0 = 0.93。对于其他三种方法，他们保持相同的参数设置。除了前两种比较方式外，他们还添加了另一种比较方式，即将竞争方法的PB设置为与LP2S相同，并比较它们的平均抽样成本。结果表明，LP2S的性能只是平庸的，在大多数情况下不如TSE或批量汤普森抽样。这表明，当K很小时，LP-FC可能没有优势。

Q: 有什么可以进一步探索的点？

A: 论文提出了几个未来研究方向，包括： 1. 分析OPT-dep和OPT-ind最优解之间的差距。关键问题是如何量化忽略非焦点臂状态的信息损失。 2. 可能将LP公式推广到奖励遵循伯努利分布以外的分布的情况。如果奖励遵循离散分布，则通过使用多项式树描述焦点臂的状态转移，可以直接推广LP。如果奖励遵循连续分布，则状态空间变为连续的，如何制定一个可行的优化问题就有些不清楚了。 3. 可能将该方法推广到上下文老虎机问题，其中框架应允许转移概率P（r，s）和动作a（r，s）取决于观察到的上下文信息。 总之，论文提出了几个有前途的研究方向，可以在批量多臂老虎机问题和更广泛的领域进行进一步探索。

Q: 总结一下论文的主要内容

A: 这篇论文提出了一种新的算法，用于解决批量多臂老虎机问题中的最佳臂识别（BAI）问题。批量多臂老虎机问题在许多现实世界的应用中出现，例如生物实验和在线营销，其中必须成批地对臂进行抽样，因为代理等待反馈的时间有限。当臂的数量很大且批次数量很少时，问题变得更加复杂。 为了解决这个问题，论文提出了以下贡献： 1. 引入了一个通用的线性规划（LP）框架，可以并入不同理论设置的最佳臂识别目标。这个框架被进一步放松为一个可以生成独立于同伴的政策的LP框架。在批量多臂老虎机文献中建立这样的LP框架和建立同伴依赖和独立政策之间的联系是前所未有的。 2. 在引入的LP框架下，指定了四种不同的设置，即PAC、SRM、FC和FB。PAC和SRM设置特别适用于大K小R的情况。 3. 提出了一个两阶段算法LP2S，具有良好的理论性质和强大的数值性能。该算法的第一阶段是一个同伴无关的过程，由LP诱导，可以通过在各个臂的累积奖励上设置阈值来有效选择好的臂。两阶段算法的期望总抽样成本为O(Lh®)，其中h®最多是R的多项式。作者还为LP的不同变体获得了合理的上限。 总之，论文通过采用更积极的臂消除方案、引入通用的LP框架以及开发具有良好理论和数值性能的两阶段算法来解决批量多臂老虎机问题中最佳臂识别的挑战。

相关文章：

Best Arm Identification in Batched Multi-armed Bandit Problems

Q: 这篇论文试图解决什么问题？ A: 这篇论文试图解决在批量多臂老虎机问题中进行最佳臂识别（BAI）的挑战，其中必须成批地对臂进行抽样，因为代理等待反馈的时间有限。这种场景出现在许多现实世界的应用中，例如…...

编程日记 2023/12/27 15:37:55

Unity编辑器紫色

紫色原因是因为编辑器内跑了其他平台的shader兼容性导致的，需要动态的去修改shader，主要用到Unity的api : Shader.Find(shaderName); 具体的工具代码如下： using System.Collections; using System.Collections.Generic; using UnityEngine…...

编程日记 2023/12/27 15:36:54

冒泡排序（C语言）

void BubbleSort(int arr[], int len) {int i, j, temp;for (i 0; i < len; i){for (j len - 1; j > i; j--){if (arr[j] > arr[j 1]){temp arr[j];arr[j] arr[j 1];arr[j 1] temp;}}} } 优化&#xff1a; 设置标志位flag&#xff0c;如果发生了交换flag设置…...

编程日记 2023/12/27 15:35:53

Unity中Shader观察空间推导（在Shader中实现）

文章目录 前言一、观察空间矩阵推导1、求观察空间基向量2、求观察空间的基向量在世界空间中的矩阵 的 逆矩阵2、求平移变换矩阵3、相乘得出 观察空间转化矩阵4、得到顶点的世界空间坐标&#xff0c;然后转化到观察空间5、把观察空间坐标转化为齐次裁剪坐标输出到屏幕 二、最终效…...

编程日记 2023/12/27 15:30:49

Hive04_DDL操作

Hive DDL操作 1 DDL 数据定义 1.1 创建数据库 CREATE DATABASE [IF NOT EXISTS] database_name [COMMENT database_comment] [LOCATION hdfs_path] [WITH DBPROPERTIES (property_nameproperty_value, ...)];[IF NOT EXISTS] &#xff1a;判断是否存在 [COMMENT database_c…...

编程日记 2023/12/27 15:29:48

odoo17核心概念view4——view.js

这是view系列的第四篇文章&#xff0c;专门介绍View组件。 作为一个Component&#xff0c;它总共包含js、css、xml三个标准文件&#xff0c;当然最重要的是view.js 首先在setup函数中对传入的参数props做了各种校验&#xff0c;然后扩展了subenv useSubEnv({keepLast: new Kee…...

编程日记 2023/12/27 15:27:46

Centos7 openSSL

阅读时长&#xff1a;10分钟 本文内容&#xff1a; 在阿里云Centos7上部署python3.10.6项目时遇到openSSL协议不支持&#xff0c;导致无法下载第三方包 本文目的&#xff1a; 通过手动编译&#xff0c;升级openssl版本centos7 重编译 python3.10.6github下载缓慢解决镜像源记录…...

编程日记 2023/12/27 15:24:44

Web 安全之文件下载漏洞详解

目录 引言 文件下载漏洞原理 文件下载漏洞的危害 文件下载漏洞类型 文件下载漏洞的利用方法 文件下载漏洞示例 文件下载漏洞的防护措施 漏洞检测与测试 小结 引言 在数字化时代&#xff0c;文件下载是网络应用程序的重要的功能之一&#xff0c;用户可以通过这一功能获…...

编程日记 2023/12/27 15:23:43

搬运机器人RFID传感器CNS-RFID-01|1S的RS485（MODBUS|HS协议）通讯连接方法

搬运机器人RFID传感器CNS-RFID-01|1S支持RS485通信&#xff0c;可支持RS485&#xff08;MODBUS RTU&#xff09;协议、RS485-HS协议&#xff0c;广泛应用于物流仓储&#xff0c;立库 AGV|无人叉车|搬送机器人等领域&#xff0c;常用定位、驻车等&#xff0c;本篇重点介绍CNS-RF…...

编程日记 2023/12/27 15:22:41

使用ZMQ.proxy实现ZMQ PUB消息转发

MQ.proxy 是 ZeroMQ 库中的一个功能&#xff0c;用于创建一个简单的代理服务器。它可以将消息从一个套接字传递到另一个套接字&#xff0c;实现消息的转发和路由。 要使用 ZMQ.proxy&#xff0c;需要按照以下步骤进行操作&#xff1a; 创建两个 ZMQ.Socket 对象&#xff1a;一个…...

编程日记 2023/12/27 15:21:41

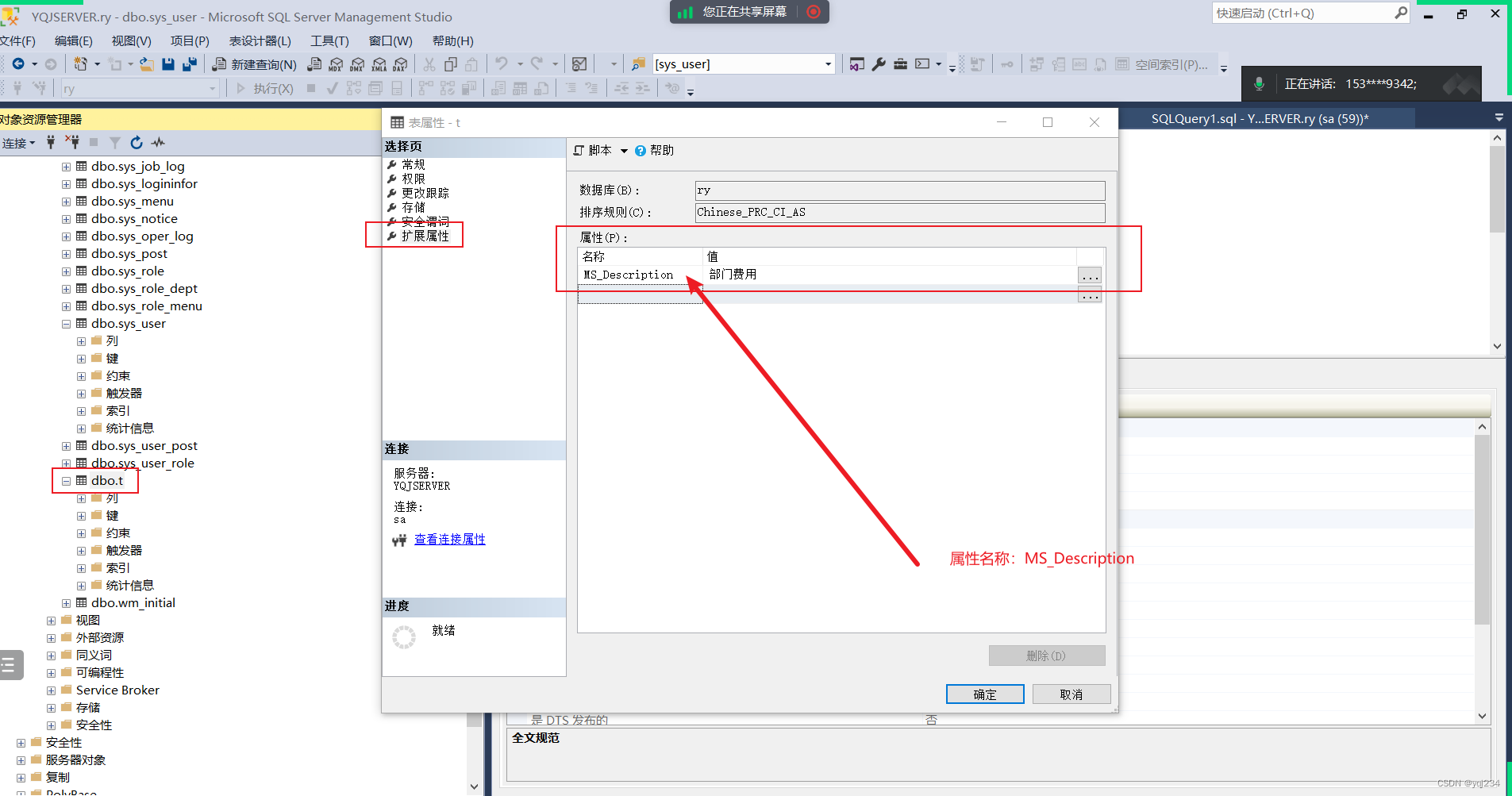
若依SQL Server开发使用教程

1. sys_menu表中的将菜单ID修改为自动ID,解决不能增加菜单的问题&#xff0c;操作流程如下&#xff1a; 解决方案如下 菜单栏->工具->选项 点击设计器&#xff0c;去掉阻止保存要求更新创建表的更改选项&#xff0c;点确认既可以保存了 2 自动生成代码找不表的解决方案…...

编程日记 2023/12/27 15:19:39

Mysql5.7服务器选项、系统变量和状态变量参考

官网地址&#xff1a;MySQL :: MySQL 5.7 Reference Manual :: 5.1.3 Server Option, System Variable, and Status Variable Reference 欢迎关注留言&#xff0c;我是收集整理小能手&#xff0c;工具翻译&#xff0c;仅供参考&#xff0c;笔芯笔芯. MySQL 5.7 参考手册 / ..…...

编程日记 2023/12/27 15:17:37

【Qt-Qss-Style】

Qt编程指南 ■ Qss■ Style■ setStyleSheet ■ style.qss■ border■ 去除弹框背景圆角■ QProgressBar样式表 ■ Qss Qt 支持很多种常见 符号 “>”代表直属子部件&#xff0c;说明两个控件之间是父子关系。 “#”代表后面的字段是前面控件类型的名称&#xff0c;当然也可…...

编程日记 2023/12/27 15:15:35

基于yolov8，制作停车位计数器(附源码)

大家好&#xff0c;YOLO(You Only Look Once) 是由Joseph Redmon和Ali开发的一种对象检测和图像分割模型。 YOLO的第一个版本于2015年发布&#xff0c;由于其高速度和准确性&#xff0c;瞬间得到了广大AI爱好者的喜爱。 Ultralytics YOLOv8则是一款前沿、最先进(SOTA)的模型&a…...

编程日记 2023/12/27 15:14:34

C++设计模式：单例模式（饿汉式、懒汉式）

单例模式是什么&#xff1f; 单例模式是一种创建型的软件设计模式。通过单例模式的设计&#xff0c;使得创建的类在当前进程中只有唯一一个实例&#xff0c;并提供一个全局性的访问点&#xff0c;这样可以规避因频繁创建对象而导致的内存飙升情况。 单例模式有三个要点 私有化…...

编程日记 2023/12/27 15:11:30

Django 访问前端页面一直在转异常：ReferenceError:axios is not defined

访问&#xff1a;http://127.0.0.1:8080/ my.html 一、异常&#xff1a; 二、原因 提示&#xff1a;axios找不到&#xff01;&#xff01; 查看代码<script src"https://unpkg.com/axios/dist/axios.min.js"></script>无法访问到官网 三、解决 Using j…...

编程日记 2023/12/27 15:08:28

C语言中关于指针的理解

#include <stdio.h> int main() {int a11;int *p&a; //因为a是整型的&#xff0c;所以我们定义指针p的时候要和a的类型一样char b;char *pa&b; //同理&#xff0c;b是字符型&#xff0c;所以这里的pa也要用字符型return 0; }因为*p指向的是地址&…...

编程日记 2023/12/27 15:01:20

MySQL MVCC精讲

版本链 我们前面说过&#xff0c;对于使用InnoDB存储引擎的表来说&#xff0c;它的聚簇索引记录中都包含两个必要的隐藏列&#xff08;row_id并不是必要的&#xff0c;我们创建的表中有主键或者非NULL的UNIQUE键时都不会包含row_id列&#xff09;&#xff1a; trx_id&#xff…...

编程日记 2023/12/27 14:55:14

如何快速删除pdf周围的空白

问题&#xff1a;写论文往往需要pdf格式的图片&#xff0c;但pdf往往四周存在大量空白需要手动截图很麻烦 解决&#xff1a; 打开命令行输入&#xff1a;pdfcrop 图片名.pdf...

编程日记 2023/12/27 14:54:12

蓝桥杯c/c++程序设计——数位排序

数位排序【第十三届】【省赛】【C组】 题目描述 小蓝对一个数的数位之和很感兴趣&#xff0c;今天他要按照数位之和给数排序。 当两个数各个数位之和不同时&#xff0c;将数位和较小的排在前面&#xff0c;当数位之和相等时&#xff0c;将数值小的排在前面。 例如&#xff0…...

编程日记 2023/12/27 14:51:09

uniapp 对接腾讯云IM群组成员管理（增删改查）

UniApp 实战&#xff1a;腾讯云IM群组成员管理&#xff08;增删改查&#xff09; 一、前言 在社交类App开发中&#xff0c;群组成员管理是核心功能之一。本文将基于UniApp框架&#xff0c;结合腾讯云IM SDK&#xff0c;详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

编程新知 2026/1/13 9:59:27

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

阿里云ACP云计算备考笔记 (5)——弹性伸缩

目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

编程新知 2026/1/22 6:07:24

可靠性+灵活性：电力载波技术在楼宇自控中的核心价值

可靠性灵活性&#xff1a;电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中&#xff0c;电力载波技术&#xff08;PLC&#xff09;凭借其独特的优势&#xff0c;正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据&#xff0c;无需额外布…...

编程新知 2025/9/27 2:43:26

（二）原型模式

原型的功能是将一个已经存在的对象作为源目标，其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现，忽略对象创建过程中的其它细节。 📌 核心特点： 避免重复初…...

编程新知 2026/2/7 10:59:04

微服务商城-商品微服务

数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

编程新知 2026/1/29 18:30:30

令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍

文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结&#xff1a; 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析&#xff1a; 实际业务去理解体会统一注…...

编程新知 2026/1/29 16:36:27

大语言模型（LLM）中的KV缓存压缩与动态稀疏注意力机制设计

随着大语言模型&#xff08;LLM&#xff09;参数规模的增长&#xff0c;推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长&#xff0c;而KV缓存的内存消耗可能高达数十GB&#xff08;例如Llama2-7B处理100K token时需50GB内存&a…...

编程新知 2026/1/28 1:40:03

第八部分：阶段项目 6：构建 React 前端应用

现在&#xff0c;是时候将你学到的 React 基础知识付诸实践&#xff0c;构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段&#xff0c;你可以先使用模拟数据&#xff0c;或者如果你的后端 API&#xff08;阶段项目 5&#xff09;已经搭建好&#xff0c;可以直接连…...

编程新知 2025/9/21 1:58:01

Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II（Linked List Cycle II）详解

文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一&#xff1a;HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二&#xff1a;Floyd 快慢指针法&#xff08;…...

编程新知 2025/8/25 19:51:15