当前位置： 首页 > news >正文

普中STM32-PZ6806L开发板(烧录方式)

news 2026/2/8 18:23:56

前言

有两种方式, 串口烧录和STLink方式烧录;

串口烧录

步骤

  1. 开发板USB转串口CH340驱动
  2. 板接线到USB连接PC
  3. 使用自带工具普中自动下载软件.exe
  4. 烧录程序到开发板
    在这里插入图片描述

ST Link方式

这种方式需要另外进行供电， 我买的如下，当年用于调试STM8的，也可以用在这次的板子上, 我板子上的串口坏掉了， 所以我目前的方式就是使用ST Link
在这里插入图片描述
接线方式如图
在这里插入图片描述
参考 Keil 问题收集

相关文章：

普中STM32-PZ6806L开发板(烧录方式)

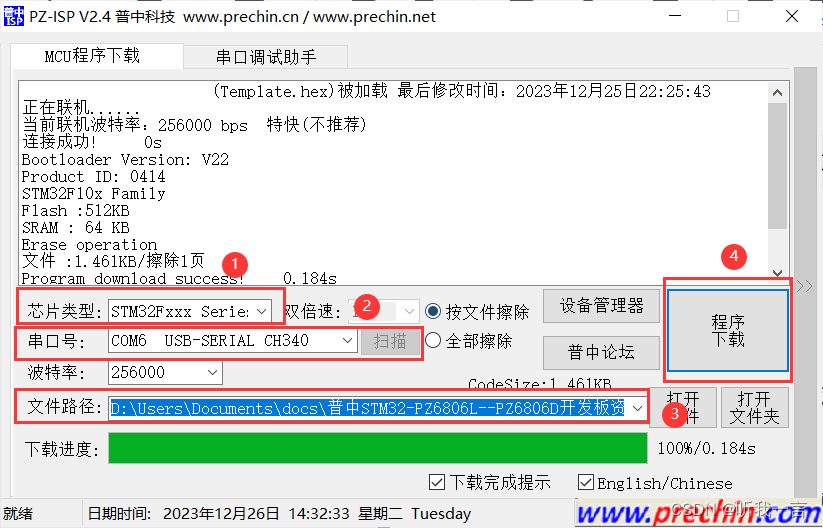
前言 有两种方式, 串口烧录和STLink方式烧录;串口烧录 步骤 开发板USB转串口CH340驱动板接线到USB连接PC使用自带工具普中自动下载软件.exe烧录程序到开发板 ST Link方式 这种方式需要另外进行供电， 我买的如下，当年用于调试STM8的，也可…...

编程日记 2023/12/28 0:56:30

基于单片机设计的指纹锁(读取、录入、验证指纹)

一、前言 指纹识别技术是一种常见的生物识别技术，利用每个人指纹的唯一性进行身份认证。相比于传统的密码锁或者钥匙锁，指纹锁具有更高的安全性和便利性，以及防止钥匙丢失或密码泄露的优势。 基于单片机设计的指纹锁项目是利用STC89C52作为…...

编程日记 2023/12/28 0:55:29

HarmonyOS - 基础组件绘制

文章目录 所有组件开发 tipsBlankTextImageTextInputButtonLoadingProgress 本文改编自&#xff1a;<HarmonyOS第一课>从简单的页面开始 https://developer.huawei.com/consumer/cn/training/course/slightMooc/C101667360160710997 所有组件 在 macOS 上&#xff0c;组…...

编程日记 2023/12/28 0:54:28

AR智慧校园三维主电子沙盘系统研究及应用

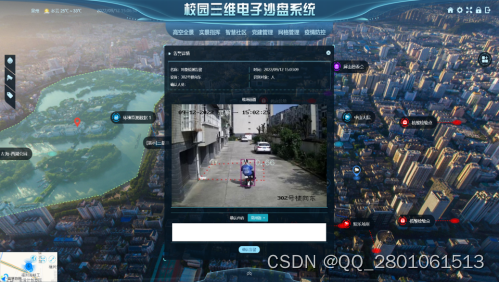
一 、概述 易图讯科技(www.3dgis.top)自主研发的智慧校园三维主电子沙盘系统&#xff0c;采用B/S架构模式&#xff0c;采用自主可控高性能WebGIS可视化引擎&#xff0c;支持多用户客户端通过网络请求访问服务器地图和专题数据&#xff0c;提供地理信息数据、专题数据的并发访问…...

编程日记 2023/12/28 0:52:26

web前端项目-七彩夜空烟花【附源码】

web前端项目-七彩动态夜空烟花【附源码】 本项目仅使用了HTML&#xff0c;代码简单&#xff0c;实现效果绚丽&#xff0c;且本项目代码直接运行即可实现&#xff0c;无需图片素材&#xff0c;接下来让我们一起实现一场美丽的烟花秀叭 运行效果&#xff1a;鼠标点击和移动可控制…...

编程日记 2023/12/28 0:45:20

在k8s中将gitlab-runner的运行pod调度到指定节点

本篇和前面的 基于helm的方式在k8s集群中部署gitlab 具有很强的关联性&#xff0c;因此如果有不明白的地方可以查看往期分享&#xff1a; 基于helm的方式在k8s集群中部署gitlab - 部署基于helm的方式在k8s集群中部署gitlab - 备份恢复基于helm的方式在k8s集群中部署gitlab - 升…...

编程日记 2023/12/28 0:42:18

1.解决父组件传数据给子组件太慢，导致子组件获取不到合适数据渲染出错问题2.vue中props传递异步数据，子组件用watch监听

vue中props传递异步数据&#xff0c;子组件用watch监听...

编程日记 2023/12/28 0:41:17

SpringMVC之获取请求参数和域对象共享数据

学习的最大理由是想摆脱平庸&#xff0c;早一天就多一份人生的精彩&#xff1b;迟一天就多一天平庸的困扰。各位小伙伴&#xff0c;如果您&#xff1a; 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持&#xff0c;想组团高效学习… 想写博客但无从下手&#xff0c;急需…...

编程日记 2023/12/28 0:39:15

IntelliJ IDEA Community（社区版）下载及安装自用版

IntelliJ IDEA Community&#xff08;社区版&#xff09;下载及安装自用版 估计是个开发都逃脱不了用IDEA的命运吧&#xff0c;这么好的软件&#xff0c;白嫖了好多年。感恩。 现在很多公司已经不让用商业版的破解版了&#xff0c;所以这里讲的是社区版。 区别&#xff1a; 商…...

编程日记 2023/12/28 0:38:14

【C语言：编译、预处理详解】

文章目录 1.编译2.预处理2.1宏定义2.1.1预定义符号2.1.2#define定义常量2.1.3#define定义宏2.1.4do-while-zero2.1.5宏的注意事项2.1.6宏与函数的对比 2.2条件编译2.3文件包含 3.offsetoff4.#与##4.1. #号4.2 ##号 1.编译 我们都知道&#xff0c;一个程序如果想运行起来要经过…...

编程日记 2023/12/28 0:37:12

【宇宙猜想】AR文创入驻今日美术馆、北京天文馆等众多展馆，在AR互动中感受科技魅力！

近日&#xff0c;由「宇宙猜想」推出的AR系列文创产品先后入驻今日美术馆、北京天文馆、国家自然博物馆、上海天文馆、国家海洋馆、中华手工展馆等各大馆场并与其展开相关合作。 「宇宙猜想」致力于创造虚拟空间价值&#xff0c;用AR技术与文创产品碰撞出新的火花&#xff0c;为…...

编程日记 2023/12/28 0:32:07

前端面试题html

HTML DOCTYPE有什么作用&#xff1f; DOCTYPE是一种指示浏览器以何种HTML或XHTML规范来解析文档的声明。它能够告知浏览器网页文档使用的标记语言的类型以及版本&#xff0c;从而确保浏览器能够正确地展示网页内容。DOCTYPE声明通常位于HTML文档的开头&#xff0c;是HTML文档…...

编程日记 2023/12/28 0:30:06

AOSP源码下载方法，解决repo sync错误：android-13.0.0_r82

篇头 最近写文章&#xff0c;反复多次折腾AOSP代码&#xff0c;因通过网络repo sync aosp代码&#xff0c;能一次顺利下载的概率很低&#xff0c;以前就经常遇到&#xff0c;但从未总结&#xff0c;导致自己也要回头检索方法&#xff0c;所以觉得可以总结一下&#xff0c;涉及…...

编程日记 2023/12/28 0:26:03

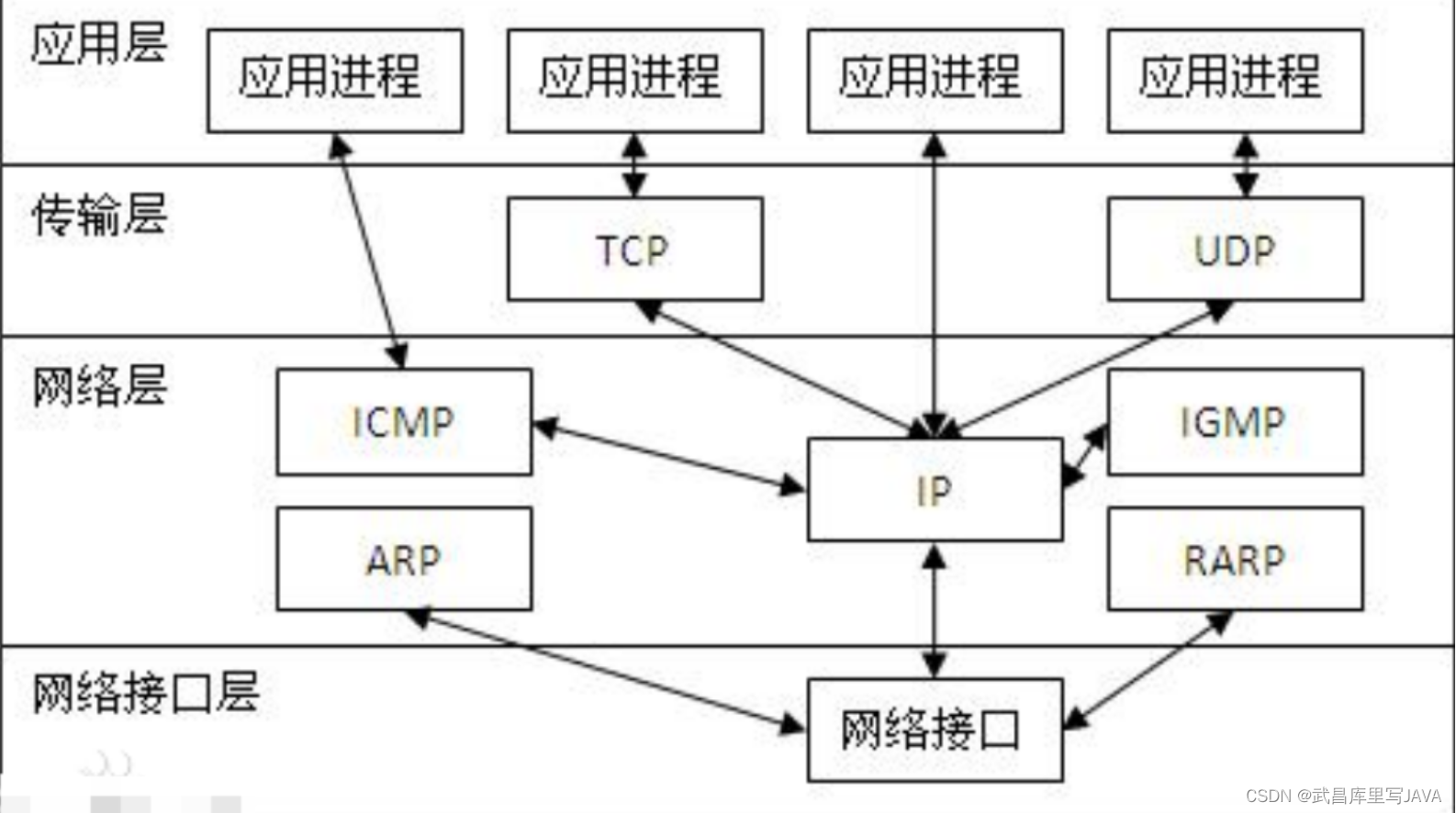
TCP:IP原理

TCP/IP 原理 TCP/IP 协议不是 TCP 和 IP 这两个协议的合称&#xff0c;而是指因特网整个 TCP/IP 协议族。从协议分层模型方面来讲&#xff0c;TCP/IP 由四个层次组成&#xff1a;网络接口层、网络层、传输层、应用层。 网络访问层(Network Access Layer) 网络访问层(Network …...

编程日记 2023/12/28 0:23:00

Java 中 Lambda 表达式的使用

目录 一、Lambda 表达式的概念 二、Lambda 表达式的语法格式 三、Lambda 表达式的案例使用 1、使用 Lambda 来实现启动线程 2、使用 Lambda 表达式实现集合的排序 3、使用 Lambda 表达式实现文件夹下的文件查找 一、Lambda 表达式的概念 Lambda 表达式是特殊的匿名内部类…...

编程日记 2023/12/28 0:10:47

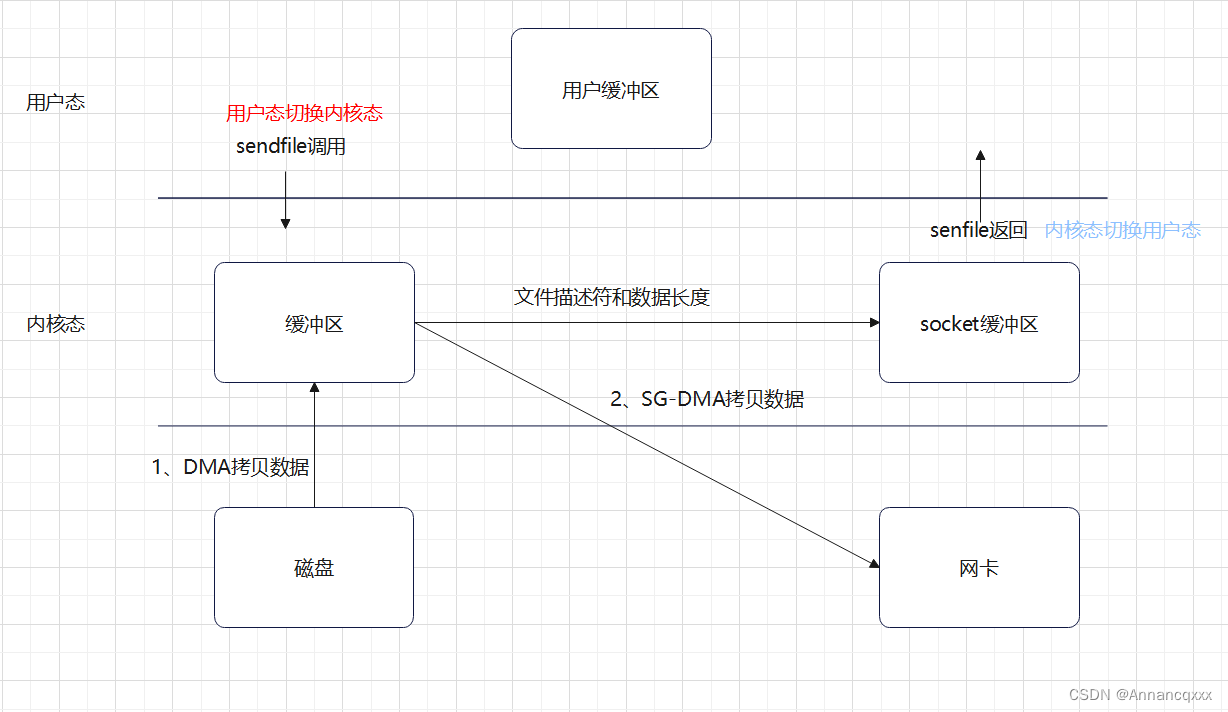
【IO】IO模型与零拷贝

前言&#xff1a; 正在运行的程序其实就是系统中的一个进程&#xff0c;操作系统会为每一个进程分配内存空间&#xff0c;而内存空间分为两部分&#xff0c;一部分是用户空间&#xff0c;这是用户进程访问的内存区域&#xff1b;另一部分是内核空间&#xff0c;是操作系统内核访…...

编程日记 2023/12/28 0:08:45

鸿蒙 - arkTs：状态管理

状态 State&#xff1a; 在声明式UI中&#xff0c;以状态驱动视图更新 状态&#xff08;State&#xff09;&#xff1a;指驱动视图更新的数据&#xff08;被装饰器标记的变量&#xff09;视图&#xff08;View&#xff09;&#xff1a;基于UI描述渲染得到的用户界面 使用示例…...

编程日记 2023/12/28 0:02:40

YOLOv5-Lite 树莓派4B 15帧教程

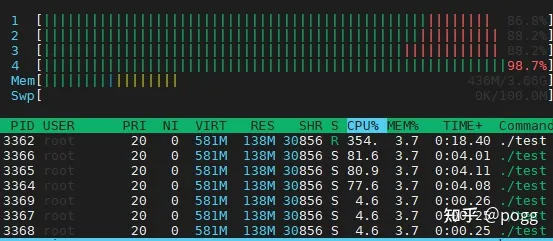
【前言】 由于v5Lite仓库遗漏了不少历史问题&#xff0c;最大的问题是毕业后卷起来了&#xff0c;找不到时间更新。 上面是这篇博客的背景&#xff0c;那么先说下结论&#xff0c;使用 v5lite-e 模型&#xff0c;在 树莓派4B&#xff08;4G内存&#xff09; 上&#xff0c;有三…...

编程日记 2023/12/28 0:01:39

2014年第三届数学建模国际赛小美赛A题吹口哨解题全过程文档及程序

2014年第三届数学建模国际赛小美赛 A题 吹口哨 原题再现&#xff1a; 哨子是一种小装置&#xff0c;当空气被迫通过开口时会发出声音。哨声的巨大而引人注目&#xff0c;使其对警察和体育裁判来说至关重要。当救生员、迷路的露营者或犯罪受害者使用它们时&#xff0c;它们可以…...

编程日记 2023/12/27 23:59:37

设计模式-注册模式

设计模式专栏 模式介绍模式特点应用场景注册模式和单例模式的区别代码示例Java实现注册模式Python实现注册模式 注册模式在spring中的应用 模式介绍 注册模式是一种设计模式&#xff0c;也称为注册树或注册器模式。这种模式将类的实例化和创建分离开来&#xff0c;避免在应用程…...

编程日记 2023/12/27 23:53:32

谷歌浏览器插件

项目中有时候会用到插件 sync-cookie-extension1.0.0&#xff1a;开发环境同步测试 cookie 至 localhost&#xff0c;便于本地请求服务携带 cookie 参考地址&#xff1a;https://juejin.cn/post/7139354571712757767 里面有源码下载下来&#xff0c;加在到扩展即可使用FeHelp…...

编程新知 2025/8/16 3:55:30

分布式增量爬虫实现方案

之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面&#xff0c;避免重复抓取&#xff0c;以节省资源和时间。 在分布式环境下&#xff0c;增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路&#xff1a;将增量判…...

编程新知 2026/2/6 1:18:56

推荐 github 项目:GeminiImageApp(图片生成方向，可以做一定的素材)

推荐 github 项目:GeminiImageApp(图片生成方向&#xff0c;可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

编程新知 2026/1/25 10:41:07

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

编程新知 2026/2/5 17:29:21

Leetcode33（ 搜索旋转排序数组）

题目表述 整数数组 nums 按升序排列&#xff0c;数组中的值 互不相同 。 在传递给函数之前&#xff0c;nums 在预先未知的某个下标 k&#xff08;0 < k < nums.length&#xff09;上进行了 旋转&#xff0c;使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

编程新知 2026/1/17 19:18:25

从物理机到云原生：全面解析计算虚拟化技术的演进与应用

前言&#xff1a;我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM&#xff08;Java Virtual Machine&#xff09;让"一次编写&#xff0c;到处运行"成为可能。这个软件层面的虚拟化让我着迷&#xff0c;但直到后来接触VMware和Doc…...

编程新知 2026/2/6 6:02:06

2025年- H71-Lc179--39.组合总和(回溯,组合）--Java版

1.题目描述 2.思路 当前的元素可以重复使用。 &#xff08;1&#xff09;确定回溯算法函数的参数和返回值&#xff08;一般是void类型&#xff09; &#xff08;2&#xff09;因为是用递归实现的&#xff0c;所以我们要确定终止条件 &#xff08;3&#xff09;单层搜索逻辑 二…...

编程新知 2026/1/22 15:25:26

前端工具库lodash与lodash-es区别详解

lodash 和 lodash-es 是同一工具库的两个不同版本&#xff0c;核心功能完全一致&#xff0c;主要区别在于模块化格式和优化方式&#xff0c;适合不同的开发环境。以下是详细对比&#xff1a; 1. 模块化格式 lodash 使用 CommonJS 模块格式&#xff08;require/module.exports&a…...

编程新知 2025/12/16 16:11:02

【Ftrace 专栏】Ftrace 参考博文

ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

编程新知 2026/1/20 3:30:27

鸿蒙Navigation路由导航-基本使用介绍

1. Navigation介绍 Navigation组件是路由导航的根视图容器&#xff0c;一般作为Page页面的根容器使用&#xff0c;其内部默认包含了标题栏、内容区和工具栏&#xff0c;其中内容区默认首页显示导航内容&#xff08;Navigation的子组件&#xff09;或非首页显示&#xff08;Nav…...

编程新知 2026/2/4 12:37:04