Scikit-Learn线性回归(一)
Scikit-Learn线性回归一
- 1、线性回归概述
- 1.1、回归
- 1.2、线性
- 1.3、线性回归
- 1.4、线性回归的优缺点
- 1.5、线性回归与逻辑回归
- 2、线性回归的原理
- 2.1、线性回归的定义与原理
- 2.2、线性回归的损失函数
- 3、Scikit-Learn线性回归
- 3.1、Scikit-Learn库
- 3.2、Scikit-Learn线性回归API
- 3.3、Scikit-Learn线性回归初体验
- 3.4、线性回归案例(波士顿房价预测)
- 4、附录
1、线性回归概述
线性回归(Linear Regression)是很基础的机器学习算法。线性回归在机器学习知识结构中的位置如下:

1.1、回归
回归(Regression)是一种应用广泛的预测建模技术,这种技术的核心在于预测的结果是连续型变量
回归是监督学习中的一个重要问题,用于预测输入变量(自变量)和输出变量(因变量)之间的关系,特别是当输入变量的值发生变化时,输出变量的值随之发生的变化,回归模型正是表示从输入变量到输出变量之间映射的函数
其中,自变量表示主动操作的变量,可以看做因变量的原因。因变量因为自变量的变化而变化,可以看做自变量的结果
回归问题的学习等价于函数拟合:选择一条函数曲线,使其很好地拟合已知数据且很好地预测未知数据
回归的目的是为了预测,比如预测明天的天气温度,预测股票的走势…
回归之所以能预测是因为他通过历史数据,摸透了“套路”,然后通过这个套路来预测未来的结果

1.2、线性
“越…,越…”,符合这种说法的就可能是线性个关系,例如,房子越大,价格就越高
但是并非所有“越…,越…”都是线性的,例如,“充电越久,电量越高”,它就类似下面的非线性曲线:

线性关系不仅仅只能存在2个变量(二维平面)。3个变量时(三维空间),线性关系就是一个平面,4个变量时(四维空间),线性关系就是一个体。以此类推…

1.3、线性回归
线性回归本身是统计学里的概念,现在经常被用在机器学习中
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方和函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析,这种函数是一个或多个被称为回归系数的模型参数的线性组合 。只有一个自变量时称为简单回归,大于一个自变量时称为多元回归
如果2个或者多个变量之间存在“线性关系”,那么我们就可以通过历史数据,摸清变量之间的“套路”,建立一个有效的模型,来预测未来的变量结果

1.4、线性回归的优缺点
优点:
- 建模速度快,不需要很复杂的计算,在数据量大的情况下依然运行速度很快
- 可以根据系数给出每个变量的理解和解释
缺点:
- 不能很好地拟合非线性数据。所以需要先判断变量之间是否是线性关系
为什么在深度学习大杀四方的今天还使用线性回归呢?
一方面,线性回归所能够模拟的关系其实远不止线性关系。线性回归中的“线性”指的是系数的线性,而通过对特征的非线性变换,以及广义线性模型的推广,输出和特征之间的函数关系可以是高度非线性的。另一方面,也是更为重要的一点,线性模型的易解释性使得它在物理学、经济学、商学等领域中占据了难以取代的地位
1.5、线性回归与逻辑回归
线性回归和逻辑回归是2种不同的经典算法。经常被拿来做比较,下面整理了一些两者的区别:
| 比较项 | 解决问题类型 | 变量类型 | 线性关系 | 表达变量关系 |
|---|---|---|---|---|
| 线性回归 | 回归 | 连续 | 符合线性关系 | 直观表达变量关系 |
| 逻辑回归 | 分类 | 离散 | 可以不符合线性关系 | 无法直观表达变量关系 |
- 线性回归只能用于回归问题,逻辑回归虽然名字叫回归,但是更多用于分类问题(关于回归与分类的区别参考文章:传送门)
- 线性回归要求因变量是连续性数值变量,而逻辑回归要求因变量是离散的变量
- 线性回归要求自变量和因变量呈线性关系,而逻辑回归不要求自变量和因变量呈线性关系
- 线性回归可以直观的表达自变量和因变量之间的关系,逻辑回归则无法表达变量之间的关系
2、线性回归的原理
2.1、线性回归的定义与原理
线性回归的定义及原理推导详见文章:传送门
2.2、线性回归的损失函数
损失函数(Loss Function),也称成本函数(Cost Function),描述的是模型的预测值与真实值的差异,并将这种差异映射为非负实数以表示模型可能带来的“风险”或“损失”。机器学习中将损失函数作为模型拟合好坏的评判准则,并通过最小化损失函数求解和评估模型
在多元线性回归中,其损失函数定义如下:
L = ∑ i = 1 m ( y i − f ( x i ) ) 2 L=\sum_{i=1}^m(y_i-f(x_i))^2 L=i=1∑m(yi−f(xi))
相关文章:

Scikit-Learn线性回归(一)
Scikit-Learn线性回归一 1、线性回归概述1.1、回归1.2、线性1.3、线性回归1.4、线性回归的优缺点1.5、线性回归与逻辑回归2、线性回归的原理2.1、线性回归的定义与原理2.2、线性回归的损失函数3、Scikit-Learn线性回归3.1、Scikit-Learn库3.2、Scikit-Learn线性回归API3.3、Sci…...

Mybatis 动态 SQL - choose, when, otherwise
有时候我们并不希望所有的条件都生效,而是只想在多个选项中选择一个。类似于Java中的switch语句,MyBatis提供了 <choose>元素。 让我们使用上面的例子,但现在如果提供了标题,则只搜索标题;如果提供了作者&a…...
idea Spring Boot项目使用JPA创建与数据库链接
1.pom.xml文件中添加依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-jpa</artifactId></dependency><dependency><groupId>com.mysql</groupId><artifactId>…...
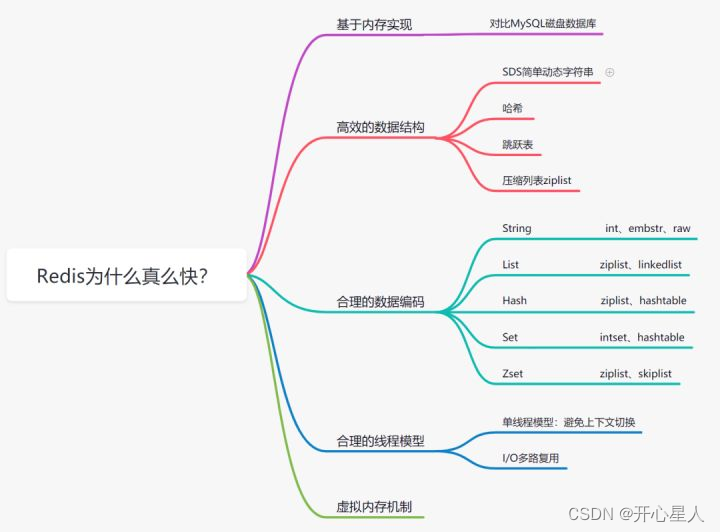
redis基础知识
学一点,整一点,基本都是综合别人的,弄成我能理解的内容 https://blog.csdn.net/liqingtx/article/details/60330555 https://blog.csdn.net/u014723137/article/details/125658176 https://redis.io/commands/ 官方命令 📌导航小助…...
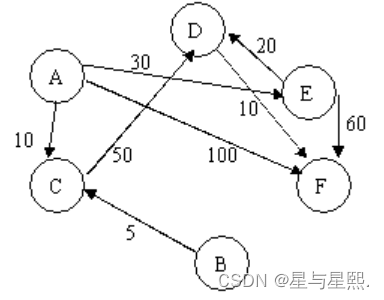
最短路径(数据结构实训)(难度系数100)
最短路径 描述: 已知一个城市的交通路线,经常要求从某一点出发到各地方的最短路径。例如有如下交通图: 则从A出发到各点的最短路径分别为: B:0 C:10 D:50 E:30 F:60 输…...
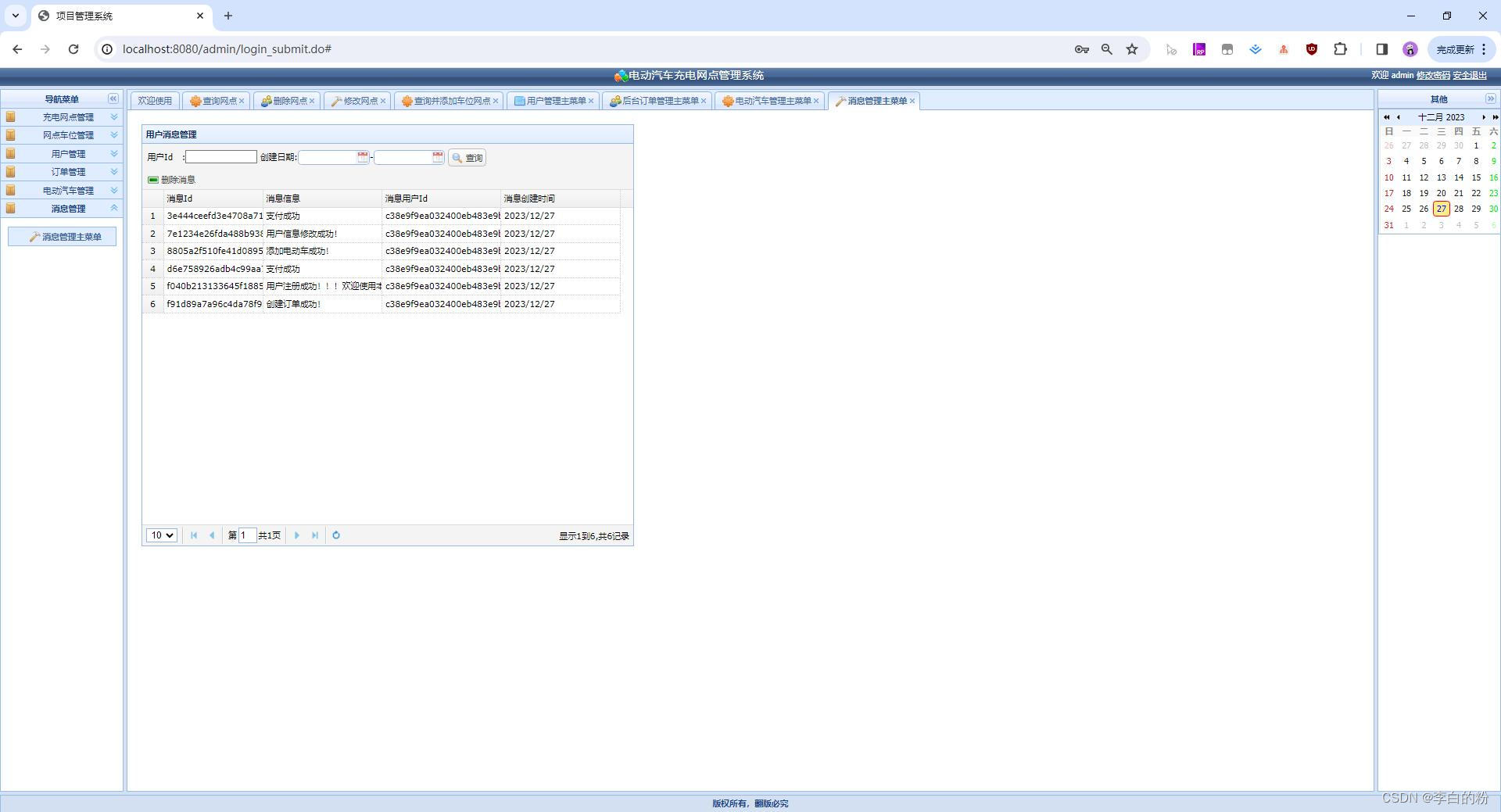
基于SSM实现的电动汽车充电网点管理系统
一、系统架构 前端:jsp | jquery | bootstrap | css 后端:spring | springmvc | jdbc 环境:jdk1.8 | mysql 二、代码及数据库 三、功能介绍 01. web端-首页 02. web端-登录 03. web端-注册 04. web端-我要充电 05. web端-个人中心-消…...
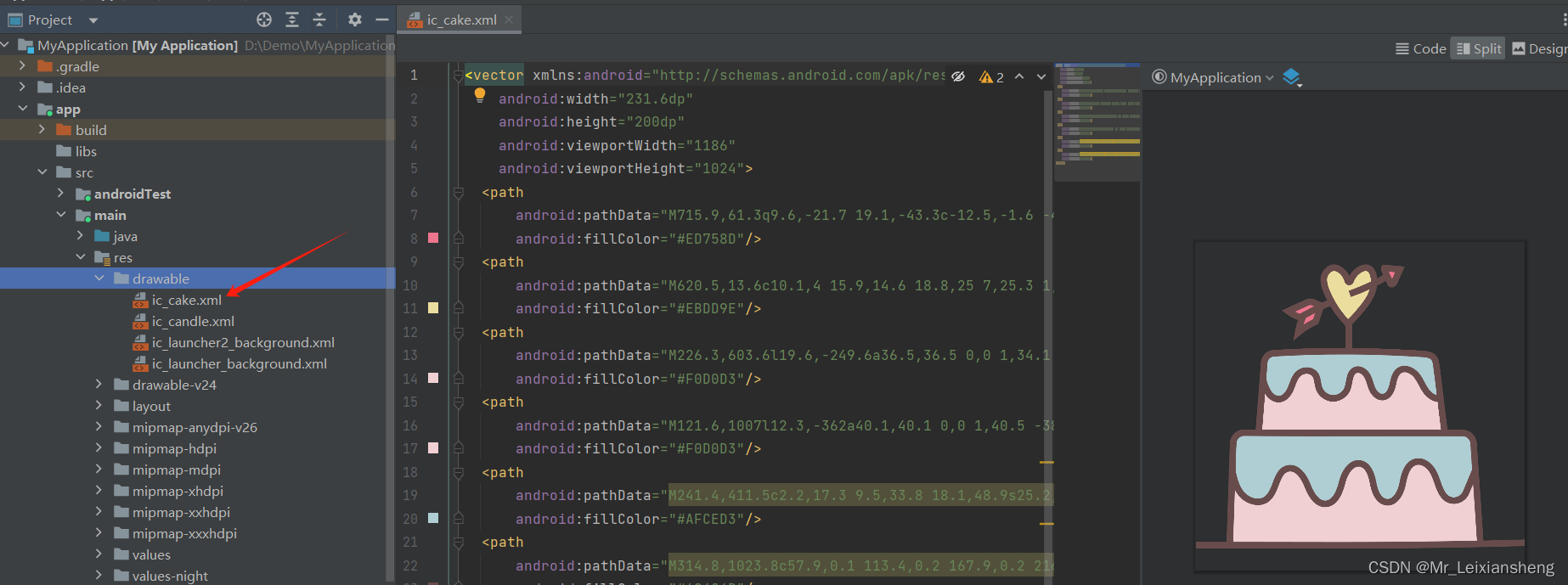
Android ImageView如何使用.svg格式图片
我们知道imageview常用的图片格式是.jpg/.png或者drawable里的部分.xml文件。但有时UI会给过来.svg格式的文件,下面讲解如何使用.svg格式图片文件 step1:AS点击File -> New -> Vector Asset step2:选中要使用的.svg文件,按需要命名和调整&#x…...

力扣热题100道-子串篇
字串 560.和为K的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续非空序列。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入&a…...

day3--Shell
1.shell语法 概论 概论 shell是我们通过命令行与操作系统沟通的语言。shell脚本可以直接在命令行中执行,也可以将一套逻辑组织成一个文件,方便复用。 AC Terminal中的命令行可以看成是一个“shell脚本在逐行执行”。Linux中常见的shell脚本有很多种&…...

【数据结构】插入排序、选择排序、冒泡排序、希尔排序、堆排序
前言:生活中我们总是会碰到各种各样的排序,今天我们就对部分常用的排序进行总结和学习,今天的内容还是相对比较简单的一部分,各位一起加油哦! 💖 博主CSDN主页:卫卫卫的个人主页 💞 ὄ…...

TiDB 7.5 LTS 发版丨提升规模化场景下关键应用的稳定性和成本的灵活性
互联网时代,数据的迅猛增长给数据库带来了可扩展性的挑战,Gen AI 带来的数据暴增更加剧了这种挑战。传统的数据分片已经不能承载新时代数据暴增的需求,更简单且具有前瞻性的方法则是采用原生分布式数据库来解决扩展性问题。在这种规模化场景的…...
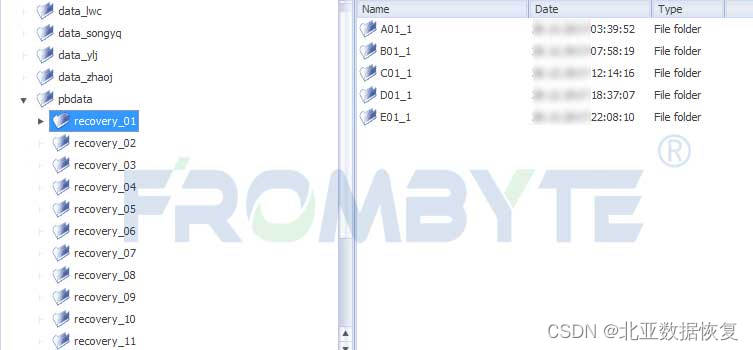
服务器数据恢复-误操作导致xfs分区数据丢失的数据恢复案例
服务器数据恢复环境: 某品牌OceanStorT系列某型号存储MD1200磁盘柜,组建的raid5磁盘阵列。上层分配了1个lun,安装的linux操作系统,划分两个分区,分区一通过lvm进行扩容,分区二格式化为xfs文件系统。 服务器…...
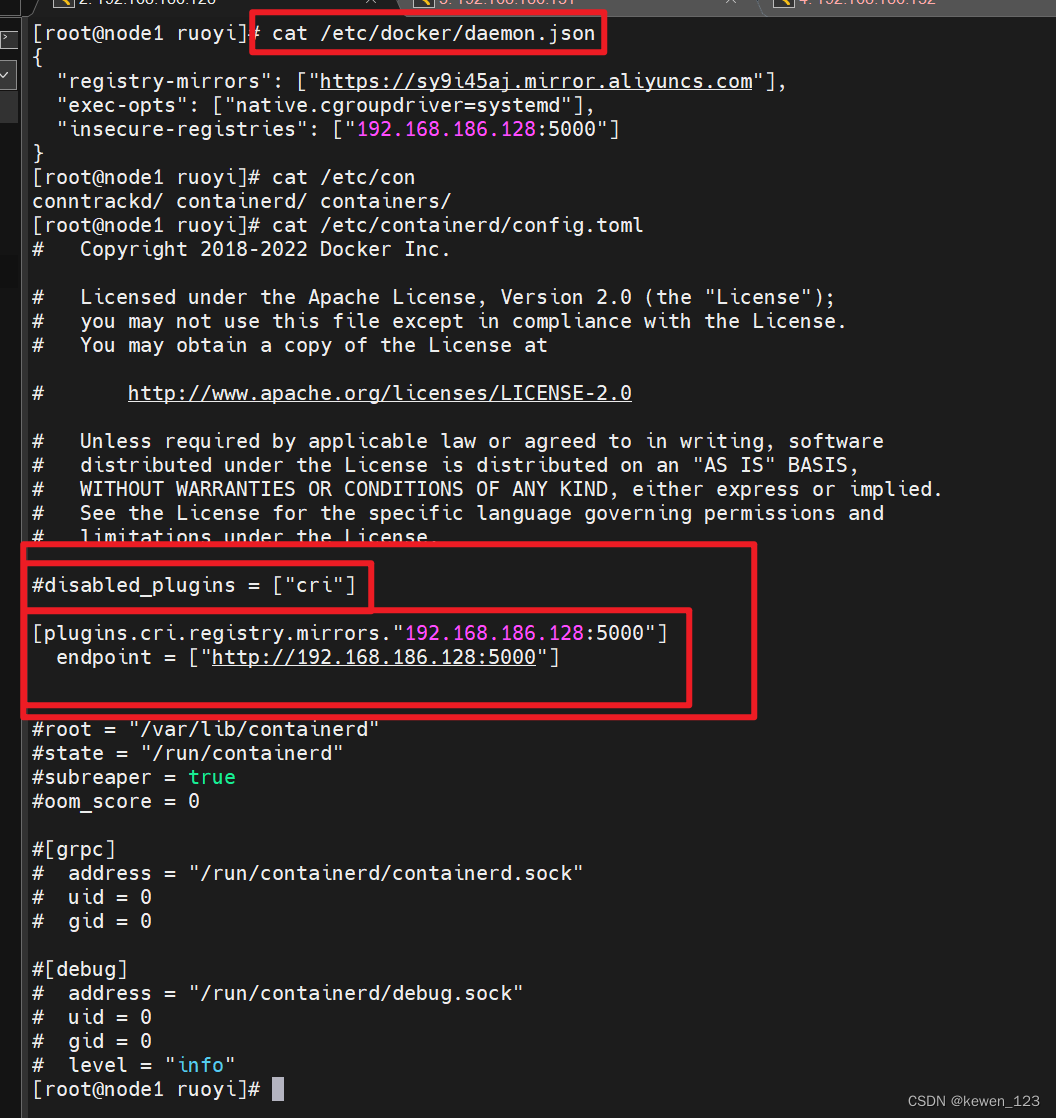
安装Kubernetes1.23、kubesphere3.4、若依项目自动打包部署到K8S记录
1.安装kubernetes1.23详细教程 kubernetes(k8s)集群超级详细超全安装部署手册 - 知乎 2.安装rancher动态存储 kubectl apply -f https://raw.githubusercontent.com/rancher/local-path-provisioner/master/deploy/local-path-storage.yaml3.安装kubesphere3.4 准备工作 您…...
 `MaterializedMySQL`同步机制解读)
(三) `MaterializedMySQL`同步机制解读
当使用 ClickHouse 的 MaterializedMySQL 引擎进行全量同步时,它主要依赖于两个关键机制:初始全量数据导入和随后的增量更新。以下是这些机制的详细解释: 初始全量数据导入 读取现有数据: 当您在 ClickHouse 中创建一个 MaterializedMySQL 类…...
)
使用 stream 流构建树(不使用递归)
你知道的越多,你不知道的越多 点赞再看,养成习惯 如果您有疑问或者见解,欢迎指教: 企鹅:869192208 文章目录 前言代码实现定义测试实体类实现方法 前言 最近遇到一个地区数据需要转换成树的需求,研究了一种…...

docker 部署 个人网页版 wps office
先声明一下,这个是用的linux桌面,然后安装了一个wps软件 安装好之后,通过我们自己的浏览器进行操作。。。。。 我只是试了一下,目前发现只能一个人用,里面还有谷歌浏览器,就是一个远程linux桌面 docker …...
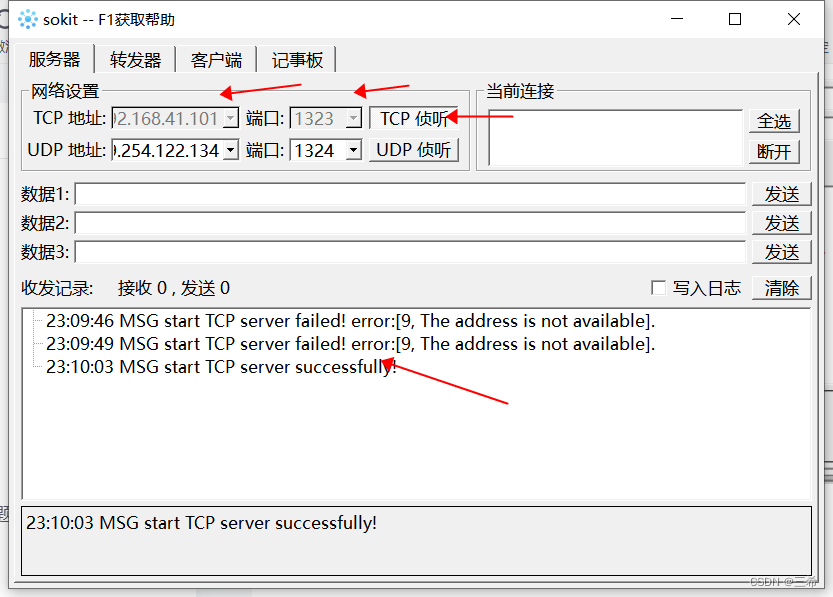
windows进行udp端口转发,解决项目中服务器收不到组播数据的问题
说明 windows7的netsh interface portproxy命令只支持tcp端口转发 如果要进行udp端口转发可以使用sokit 运行sokit 端口转发(以为tcp作为讲解,udp类似) 选择转发器 输入监听地址(SRC地址)和端口 输入转发地址&am…...

抖音、小红书、视频号是如何判定是否限流的?
在这个新媒体营销的时代,抖音、小红书和视频号作为中国最受欢迎的社交媒体平台,为品牌和内容创作者提供了极具潜力的展示空间。然而,无论在哪个平台,限流成为很多人的苦恼。 抖音的推荐算法基于人群画像和初始流量池,同…...
)
frida native hook 技术( frida hook so层函数)
什么是hook: hook,中文译作”钩子“,”挂钩“,看起来好像和钓鱼有点关系,其实它更像一张网。想象这样一个场景:我们在河流上筑坝,只留一个狭窄的通道让水流通过,在这个通道上设一张网…...
-- 多环境开发(yml多文件版))
SpringBoot运维(三)-- 多环境开发(yml多文件版)
目录 引言: 1. 多环境开发的配置 2. 多环境开发--根据功能拆分配置文件 引言: 多环境? 其实就是说你的电脑上写的程序最终要放到别人的服务器上去运行。每个计算机环境不一样...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
