当前位置： 首页 > news >正文

【数据库系统概论】第6章-关系数据库理论

news 2026/2/8 6:33:14

真别看吧，抄ppt而已啊

文章目录

    • 6.1 引言
    • 6.2 规范化
      • 6.2.1 函数依赖
      • 6.2.2 码
      • 6.2.3 范式（Normal Form）
      • 6.2.4 BC范式
      • 6.2.5 规范化小结

6.1 引言

我们有这样一张表：
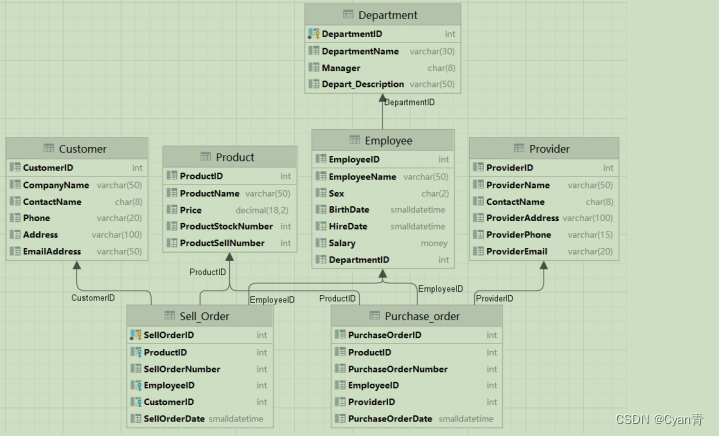
在这里插入图片描述
but 为啥这样设计呢？由此引出怎样设计一个关系数据库的问题。
进而出现：数据库逻辑设计的工具——关系数据库的规范化理论。
关系数据库有严格的理论支撑，这也是它的过人之处。

  • 回顾关系模式
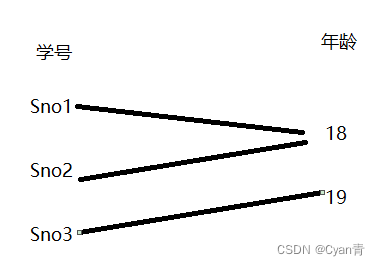
    在这里插入图片描述
    在这里插入图片描述
  • 数据依赖
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    根据上图，关系中的映射不一定是单射的，即y不能确定x。（可能处于既不满也不单的混合态）
    单射、满射、双射
    X -> Y，可以认为知道了元组的X就能确定它的Y。
  • 且看下面的问题
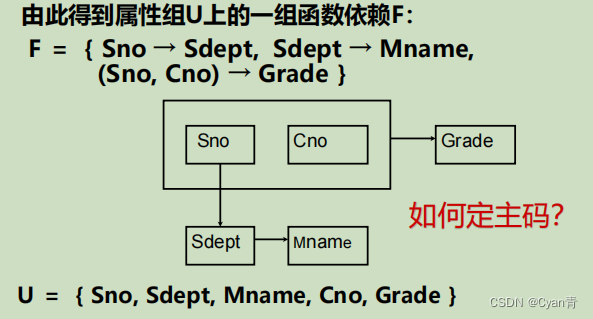
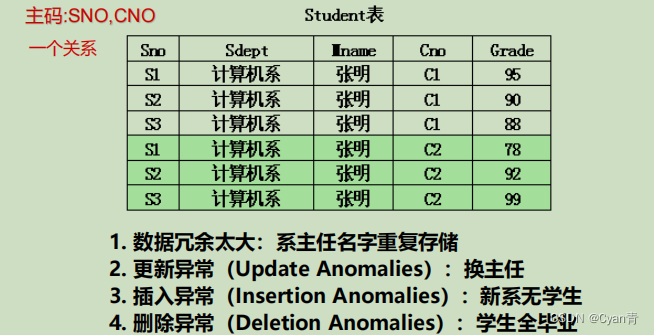
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    这是一个关系模式，而且不咋地。
    Q: 怎么让它变好呢？
    A: 通过分解关系模式来消除其中不合适的数据依赖。
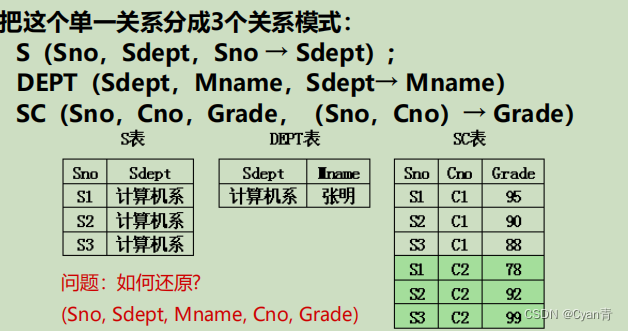
    在这里插入图片描述
    为什么这样分解就好呢？
    引入关系规范化

6.2 规范化

6.2.1 函数依赖

  1. 定义
    在这里插入图片描述
  2. 解释
    在这里插入图片描述
  3. 平凡与非平凡函数依赖
    在这里插入图片描述
    在这里插入图片描述
  4. 完全函数与部分函数依赖
    在这里插入图片描述
    在这里插入图片描述
  5. 传递函数依赖
    在这里插入图片描述
    事实上，如果 Y 是 X的子集或者，Y->X，那么X是直接函数决定Z的。
    在这里插入图片描述

6.2.2 码

  • 主码、候选码
    在这里插入图片描述
    在这里插入图片描述
  • 主属性、非主属性、全码
    在这里插入图片描述
    在这里插入图片描述
  • 外码
    在这里插入图片描述
  • 习题
    在这里插入图片描述
    AC -> A, AC -> C,
A -> B => AC -> BC => AC -> D
从而 AC -> U， AC为码

6.2.3 范式（Normal Form）

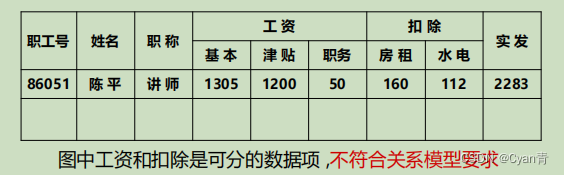
在这里插入图片描述

  • 1NF
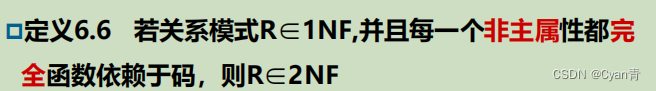
    在这里插入图片描述
    反例：
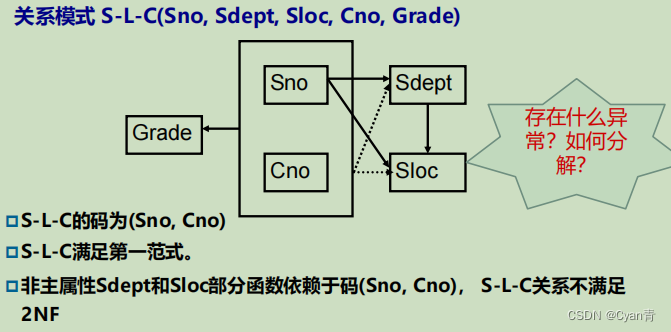
    在这里插入图片描述

  • 2NF
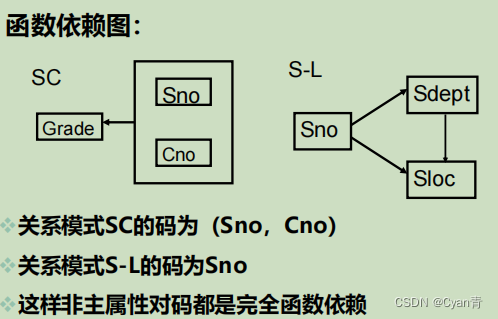
    在这里插入图片描述
    反例：
    在这里插入图片描述
    坏处：
    在这里插入图片描述
    解决方法：
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

  • 3NF

  1. 定义
    在这里插入图片描述
    在这里插入图片描述
    直白点说，sdept能确定sloc，你把sloc与sdept 放在一张表里是多余的，放到(sdept,sloc)这张表里一条就够了。
  2. 存在问题
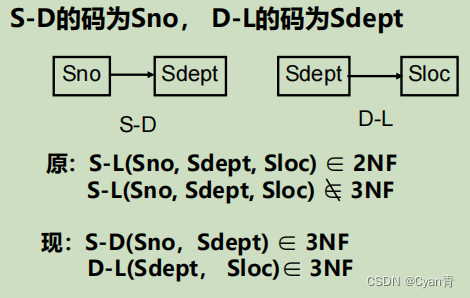
    在这里插入图片描述
  3. 解决办法
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
  • 习题
    在这里插入图片描述
    在这里插入图片描述

6.2.4 BC范式

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

6.2.5 规范化小结

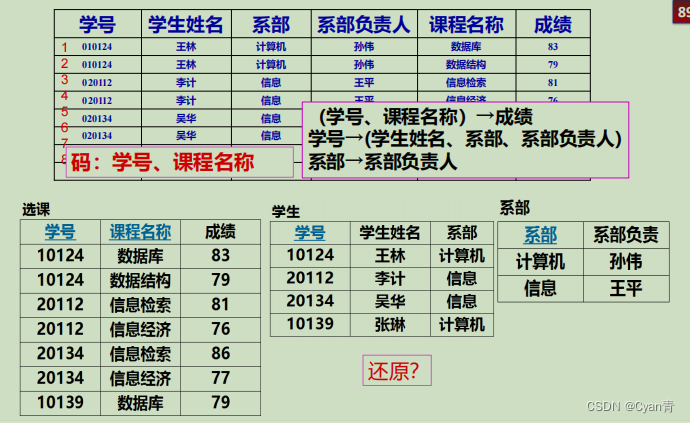
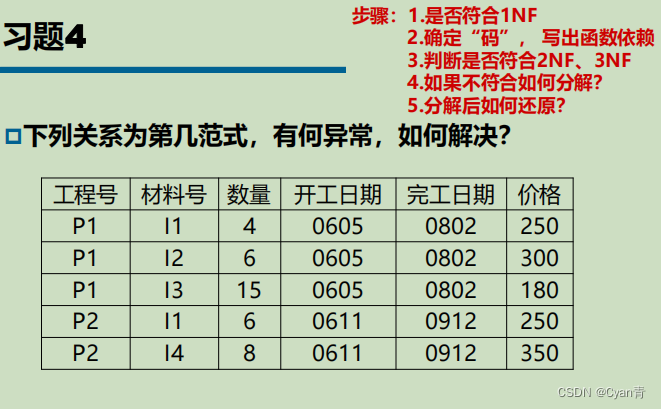
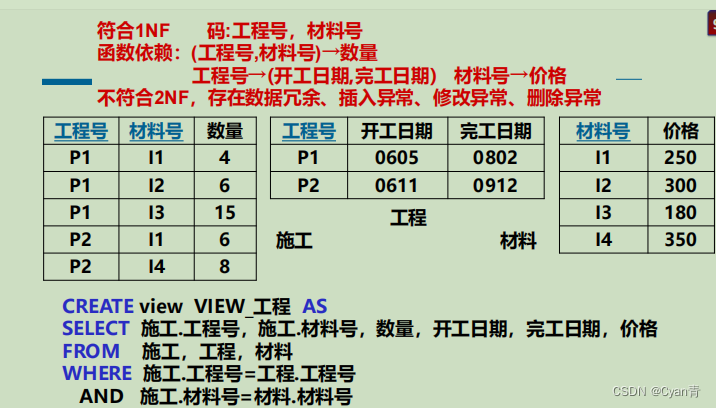
在这里插入图片描述
在这里插入图片描述

  • 习题
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

分成若干子表以后要多设一个表来保存二者之间的关系。

相关文章：

【数据库系统概论】第6章-关系数据库理论

真别看吧，抄ppt而已啊 文章目录 6.1 引言6.2 规范化6.2.1 函数依赖6.2.2 码6.2.3 范式（Normal Form）6.2.4 BC范式6.2.5 规范化小结 6.1 引言 我们有这样一张表： but 为啥这样设计呢？由此引出怎样设计一个关系数据库…...

编程日记 2023/12/29 22:37:30

算法设计与分析实验报告-贪心算法

校课程的简单实验报告。 算法设计与分析实验报告-递归与分治策略 算法设计与分析实验报告-动态规划算法 算法设计与分析实验报告-贪心算法 dijkstra迪杰斯特拉算法（邻接表法） 算法设计与分析实验报告-回溯法 算法设计与分析实验报告-分支限界法 …...

编程日记 2023/12/29 22:35:28

Unity读取服务器声音文件

Unity读取服务器声音文件 功能1.在网站的根目录放置一个声音文件Alarm01.wav（这个是window系统自带的找不到这个格式的可以直接在C盘搜索）2.在WebManager.cs脚本中添加clipPath、audio、m_downloadClip属性和DownloadSound（）函数&…...

编程日记 2023/12/29 22:28:19

掌握ElasticSearch（一）：Elasticsearch安装与配置、Kibana安装

文章目录 〇、简介1.Elasticsearch简介2.典型业务场景3.数据采集工具4.名词解释 一、安装1.使用docker(1)创建虚拟网络(2)Elasticsearch安装步骤 2.使用压缩包 二、配置1.目录介绍2.配置文件介绍3.elasticsearch.yml节点配置4.jvm.options堆配置 二、可视化工具Kibana1.介绍2.安…...

编程日记 2023/12/29 22:25:16

《剑指offer》Java版--13.机器人的运动范围（BFS）

剑指offer原题13:机器人的运动范围 地上有一个m行n列的方格。一个机器人从坐标(0,0)的格子开始移动，它每次可以向左、右、上、下移动一格，但不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时,机器人能够进入方格(35,37),因为353…...

编程日记 2023/12/29 22:22:14

基于流程挖掘的保险理赔优化策略实践

引言 在当今日益竞争的商业环境中，保险公司面临着日益增长的业务量和客户期望的挑战。特别是在理赔领域，理赔是保险行业的重要环节，也是保险公司和客户之间最直接的联系点。然而，长周期和繁琐的理赔流程常常给保险公司和投保人带来困扰。因此，如何提供准确且高效的理赔处…...

编程日记 2023/12/29 22:20:11

Docker五 | DockerFile

目录 DockerFile 常用保留字 FROM MAINTAINER RUN EXPOSE WORKDIR USER ENV VOLUME ADD COPY CMD ENTRYPOINT DockerFile案例 前期准备 编写DockerFile文件 运行DockerFile 运行镜像 DockerFile是用来构建Docker镜像的文本文件，是由一条条构建…...

编程日记 2023/12/29 22:18:10

2023年度总结：技术旅程的杨帆远航⛵

文章目录 职业规划与心灵成长 ❤️‍🔥我的最大收获与成长 💪新年Flag 🚩我的技术发展规划 ⌛对技术行业的深度思考 🤔祝愿 🌇 2023 年对我来说是一个充实而令人难以忘怀的一年。这一年，我在CSDN上发表了 1…...

编程日记 2023/12/29 22:13:06

SpringBoot+AOP+Redis 防止重复请求提交

本文项目基于以下教程的代码版本&#xff1a; https://javaxbfs.blog.csdn.net/article/details/135224261 代码仓库: springboot一些案例的整合_1: springboot一些案例的整合 1、实现步骤 2.引入依赖 我们需要redis、aop的依赖。 <dependency><groupId>org.spr…...

编程日记 2023/12/29 22:12:05

偷流量、端口占用、网络负载高、socket创建释放异常等Android高阶TCP/IP网络问题定位思路

一&#xff0c;背景 通常一些偷流量、端口占用、网络负载高、socket创建释放异常等Android网络相关问题&#xff0c;可以通过使用tcpdump抓tcp/ip报文&#xff0c;来定位。但是tcpdump无进程信息&#xff0c;也没有APK包名信息&#xff0c;无法确认异常的报文来自哪些Apk或者n…...

编程日记 2023/12/29 22:09:02

《人人都能用英语》学习笔记

https://github.com/xiaolai/everyone-can-use-english 核心&#xff1a; 用 What──它究竟是什么&#xff1f;Why──为什么它是那个样子&#xff1f;How──要掌握它、应用它&#xff0c;必须得遵循什么样的步骤&#xff1f; 在运行程序之前&#xff0c;要反复浏览代码&a…...

编程日记 2023/12/29 22:08:02

NFC与ZigBee技术在智慧农业物联网监测系统中的应用

近年来&#xff0c;我国农业物联网技术飞速发展&#xff0c;基于物联网技术的智能农业监测系统有望得到较大规模的推广应用。但传统的物联网农业监测系统其网络结构层次单一&#xff0c;多采用基于有线或无线结构的节点-上位机数据采集模式&#xff0c;节点数据访问模式缺乏灵活…...

编程日记 2023/12/29 22:03:58

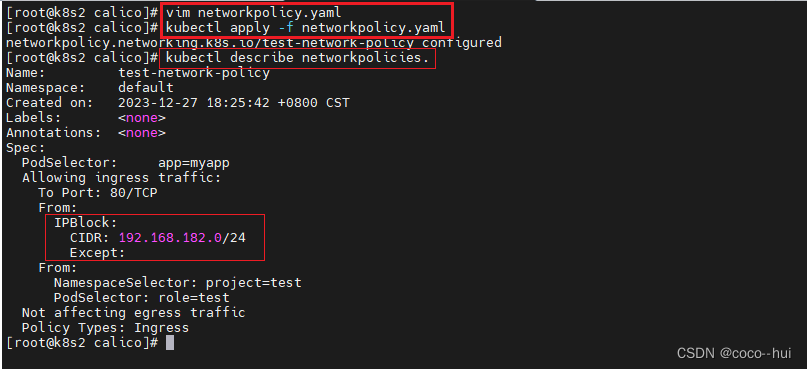
k8s-cni网络 10

Flannel vxlan模式跨主机通信原理 在同一个节点上的pod 流量通过cni网桥可以直接进行转发&#xff1b; 在需要跨主机访问时&#xff0c;数据包通过flannel(隧道) 知道另一边的mac地址&#xff0c;就可以拿到另一边的ip地址&#xff0c;然后构建常规的以太网数据包&#xff0c;…...

编程日记 2023/12/29 22:01:56

听GPT 讲Rust源代码--src/tools(27)

File: rust/src/tools/clippy/clippy_lints/src/methods/suspicious_to_owned.rs 文件rust/src/tools/clippy/clippy_lints/src/methods/suspicious_to_owned.rs的作用是实施Clippy lint规则&#xff0c;检测产生潜在性能问题的字符转换代码&#xff0c;并给出相关建议。 在Rus…...

编程日记 2023/12/29 22:00:55

经济危机下，我们普通人如何翻身？2024创业新风口，适合普通人的创业项目

明年的商业环境会比今年更残酷&#xff0c;不是贩卖危机。旅游行业还在刺激性消费&#xff0c;再过几个月大家就没钱了&#xff0c;估计慢慢也消停。中小微企业资金链断裂&#xff0c;大部分公司倒闭&#xff0c;大批人失业&#xff0c;所以经济恢复需要一个周期。 30年河东&am…...

编程日记 2023/12/29 21:58:53

深入浅出图解C#堆与栈 C# Heap(ing) VS Stack(ing) 第五节 引用类型复制问题及用克隆接口ICloneable修复

深入浅出图解C#堆与栈 C# Heaping VS Stacking 第五节 引用类型复制问题及用克隆接口ICloneable修复 [深入浅出图解C#堆与栈 C# Heap(ing) VS Stack(ing) 第一节 理解堆与栈](https://mp.csdn.net/mdeditor/101021023)[深入浅出图解C#堆与栈 C# Heap(ing) VS Stack(ing) 第二节…...

编程日记 2023/12/29 21:56:51

python中基本元素的pop函数

python中基本元素的pop函数 一、列表List二、元组Tuple三、字典dict四、集合set 一、列表List pop() 根据索引删除并返回被删除的元素&#xff0c;索引默认为-1 a [1, 2, 3, 2, 5] b a.pop() # b5&#xff0c;默认返回最后一个值 print(b) b a.pop(2) # b3,返回a[2] pri…...

编程日记 2023/12/29 21:55:50

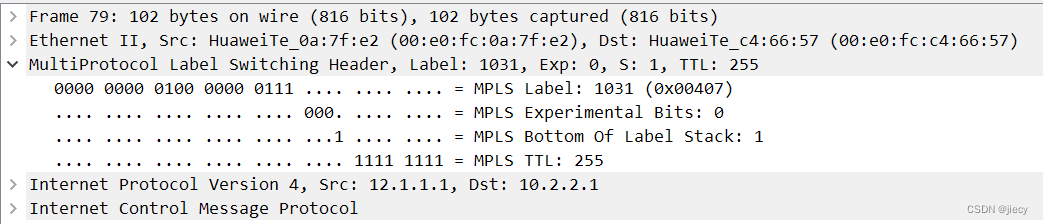
MPLS动态协议LDP配置示例

一、预习&#xff1a; MPLS是一种根据报文中携带的标签来转发数据的技术&#xff0c;两台LSR必须在它们之间转的数据 的标签使用上“达成共识”。LSR之间可以运行LDP来告知其他LSR本设备上的标签绑定信息&#xff0c;从而实现标签报文的正确转发。 LSR&#xff1a;Label Switch…...

编程日记 2023/12/29 21:48:44

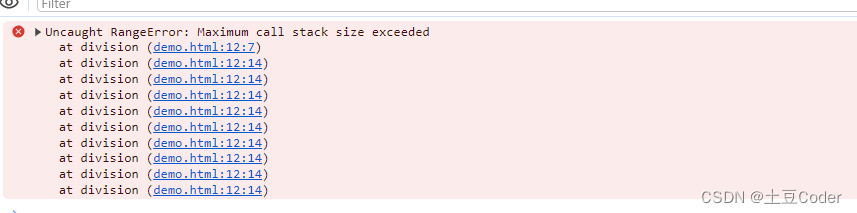
JS调用栈：为何会栈溢出

JS调用栈&#xff1a;为何会栈溢出 JS调用栈什么是函数调用什么是栈在开发中利用调用栈栈溢出 JS调用栈 JavaScript 经常会出现一个函数中调用另外一个函数的情况&#xff0c;调用栈就是用来管理函数调用关系的一种数据结构&#xff0c;首先你要先弄明白函数调用和栈结构 什么…...

编程日记 2023/12/29 21:47:43

代码随想Day52 | 300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组

300.最长递增子序列 这道题目的重点在于动态数组的定义 dp[i]&#xff1a;以nums[i]为结尾的最长递增子序列&#xff0c;因为这样定义可以进行递推&#xff1b; 递推&#xff1a;j从0-i进行对比&#xff0c;如果nums[i]大于nums[j]&#xff0c;dp[i]dp[j]1&#xff1b; 初始化…...

编程日记 2023/12/29 21:45:41

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

Prompt Tuning、P-Tuning、Prefix Tuning的区别

一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning（提示调优） 核心思想：固定预训练模型参数，仅学习额外的连续提示向量（通常是嵌入层的一部分）。实现方式：在输入文本前添加可训练的连续向量（软提示），模型只更新这些提示参数。优势：参数量少（仅提…...

编程新知 2026/2/8 1:14:13

Zustand 状态管理库：极简而强大的解决方案

Zustand 是一个轻量级、快速和可扩展的状态管理库&#xff0c;特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

编程新知 2026/1/26 19:01:00

逻辑回归：给不确定性划界的分类大师

想象你是一名医生。面对患者的检查报告&#xff08;肿瘤大小、血液指标&#xff09;&#xff0c;你需要做出一个**决定性判断**&#xff1a;恶性还是良性&#xff1f;这种“非黑即白”的抉择&#xff0c;正是**逻辑回归&#xff08;Logistic Regression&#xff09;** 的战场&a…...

编程新知 2025/10/27 21:25:04

最新SpringBoot+SpringCloud+Nacos微服务框架分享

文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的&#xff0c;根据Excel列的需求预估的工时直接打骨折&#xff0c;不要问我为什么&#xff0c;主要…...

编程新知 2026/2/1 23:39:12

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表

1、行为树节点分类 在 Nav2（Navigation2）的行为树框架中，行为树节点插件按照功能分为 Action（动作节点）、Condition（条件节点）、Control（控制节点） 和 Decorator（装饰节点） 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务，直接与硬件、传感器或外部系统…...

编程新知 2026/2/7 8:45:41

2021-03-15 iview一些问题

1.iview 在使用tree组件时&#xff0c;发现没有set类的方法&#xff0c;只有get&#xff0c;那么要改变tree值&#xff0c;只能遍历treeData&#xff0c;递归修改treeData的checked&#xff0c;发现无法更改&#xff0c;原因在于check模式下&#xff0c;子元素的勾选状态跟父节…...

编程新知 2026/2/5 3:29:13

爬虫基础学习day2

# 爬虫设计领域 工商&#xff1a;企查查、天眼查短视频&#xff1a;抖音、快手、西瓜 ---> 飞瓜电商&#xff1a;京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空&#xff1a;抓取所有航空公司价格 ---> 去哪儿自媒体&#xff1a;采集自媒体数据进…...

编程新知 2025/12/5 3:38:11

C/C++ 中附加包含目录、附加库目录与附加依赖项详解

在 C/C 编程的编译和链接过程中&#xff0c;附加包含目录、附加库目录和附加依赖项是三个至关重要的设置&#xff0c;它们相互配合&#xff0c;确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中&#xff0c;这些概念容易让人混淆&#xff0c;但深入理解它们的作用和联…...

编程新知 2026/1/26 2:22:24

Python 高级应用10：在python 大型项目中 FastAPI 和 Django 的相互配合

无论是python&#xff0c;或者java 的大型项目中&#xff0c;都会涉及到 自身平台微服务之间的相互调用&#xff0c;以及和第三发平台的 接口对接&#xff0c;那在python 中是怎么实现的呢&#xff1f; 在 Python Web 开发中&#xff0c;FastAPI 和 Django 是两个重要但定位不…...

编程新知 2025/10/26 4:25:02