免费在线客服软件推荐:经济实用的客户沟通解决方案
好用的在线客服软件是企业是必不可少的工具,他让企业流程更流畅高效,让客户服务更完善优质。市场上的在线客服软件有很多,说着免费使用的软件也不在少数。今天小编就来推荐一款免费在线客服软件。
不过,我们选择免费在线客服软件要知晓的一点是,免费和付费的区别就是功能上的限制,如果您的企业需求较多且个性化,付费版的在线客服系统是更好的选择。如果您的需求简单且单一,或者想先试试看,免费在线客服软件Zoho Desk免费在线客服软件则是您的企业的不二选择。
一、挑选免费在线客服软件要看哪些标准?
1、首先要看免费版本的使用时长、客服的限制人数。
2、要看免费版本的功能是否能满足基础需求,若是无法满足,那么会非常影响您的使用体验。
3、看它是否同样提供售后服务支持,完善的售后服务能随时解决使用问题。
4、使用同类产品还要注意其对数据隐私安全的保护,防止企业内部数据泄露造成损失。(延伸阅读:中小型外贸企业怎么选择客户服务系统?)
二、免费在线客服软件有哪些功能?
Zoho Desk免费在线客服软件具备以下功能特点:
1、免费版客服系统可以同时加3个客服,适合初创企业、小企业。如果您的客服人数较多,标准版、专业版、企业版也不限制客服人数的添加。
2、您可以永久使用免费版Zoho Desk在线客服软件,无需担心时间限制。
3、此外,您能查看工单记录、添加工单评论等,充分了解工单进展;能添加帮助中心,支持客户自助服务;能自定义首选项设置,包括帮助台设置、字体设置;还能智能管理、搜索客户信息,使用Radar移动应用,方便客服工作展开等等。
4、即便是免费版本,Zoho(卓豪)也会为您提供完善、全面的售后服务支持,解决您的任何问题。
相关文章:

免费在线客服软件推荐:经济实用的客户沟通解决方案
好用的在线客服软件是企业是必不可少的工具,他让企业流程更流畅高效,让客户服务更完善优质。市场上的在线客服软件有很多,说着免费使用的软件也不在少数。今天小编就来推荐一款免费在线客服软件。 不过,我们选择免费在线客服软件…...

leetcode344. 反转字符串
题目描述 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。 不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。 示例 1: 输入:s ["h&quo…...

【js自定义鼠标样式】【js自定义鼠标动画】
文章目录 前言一、效果图二、实现步骤1. 去除原有鼠标样式2. 自定义鼠标样式3. 使用 总结 前言 自定义鼠标形状,自定义鼠标的动画,可以让我们的页面更加有设计感。 当前需求:吧鼠标自定义成一个正方形,鼠标的效果有:和…...

Linux开发工具——gdb篇
Linux下调试工具——gdb 文章目录 makefile自动化构建工具 gdb背景 gdb的使用 常用命令 总结 前言: 编写代码我们使用vim,编译代码我们使用gcc/g,但是我们,不能保证代码没问题,所以调试是必不可少的。与gcc/vim一样&…...

spring状态机
1、概述 Spring State Machine 是一个用于处理状态机逻辑的框架,它提供了一种简洁的方法来定义状 态、转换以及在状态变更时触发的动作。 概念 状态 ( State ) :一个状态机至少要包含两个状态。例如自动门的例子,有 …...
K8S异常处理
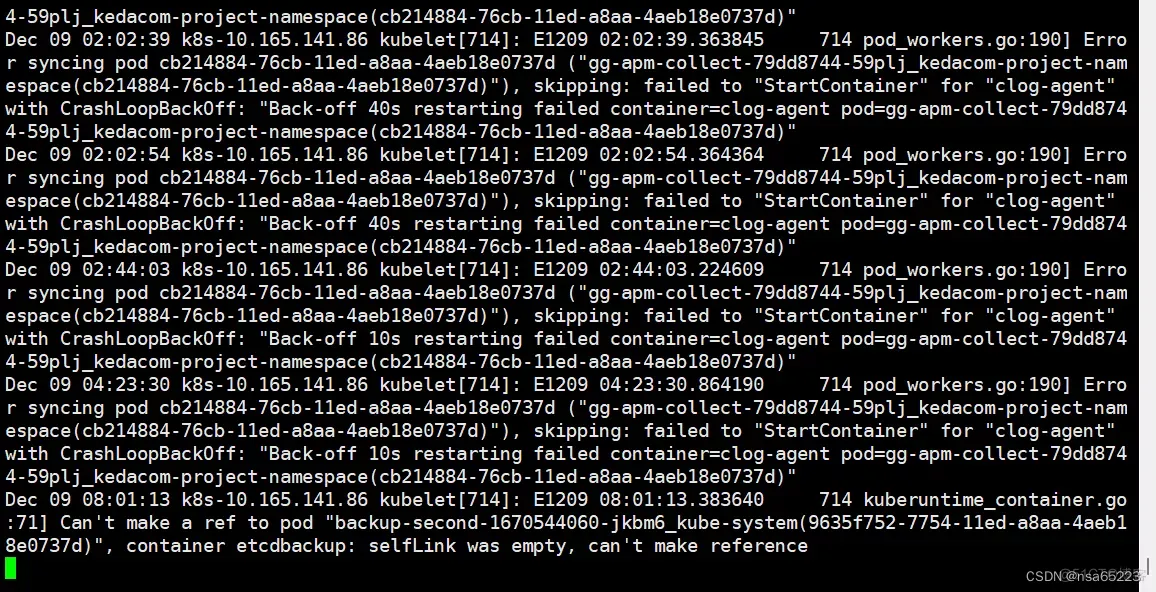
一、概述 1、k8s有时候会报错The connection to the server ip:6443 was refused - did you specify the right host or port ,本文档提供几种可能产生该报错的原因和排障思路。 二、发现问题 使用任意Kubectl 命令会报错:The connection to the serv…...
【挑战全网最易懂】深度强化学习 --- 零基础指南
深度强化学习介绍、概念 强化学习介绍离散场景,使用行为价值方法连续场景,使用概率分布方法实时反馈连续场景:使用概率分布 行为价值方法 强化学习六要素设计奖励函数设计评论家策略学习与优化 算法路径深度 Q 网络 DQN演员-评论家算法&…...

WPF RelativeSource
RelativeSource 类在 WPF 中提供了以下几种模式: RelativeSource Self:指定当前元素作为相对源。可以在当前元素的属性中绑定到自身的属性。 示例: <TextBlock Text"{Binding Text, RelativeSource{RelativeSource Self}}" /&…...

centos 安装 配置 zsh
centos 编译安装 zsh 和 配置 oh-my-zsh 下载 wget https://jaist.dl.sourceforge.net/project/zsh/zsh/5.9/zsh-5.9.tar.xz依赖 yum install ncurses-devel安装zsh 执行: tar -xvf zsh-5.9.tar.xz cd zsh-5.9 ./configure --prefix/usr/local/zsh5.9 make &am…...
git 常用基本命令, reset 回退撤销commit,解决gitignore无效,忽略记录或未记录远程仓库的文件,删除远程仓库文件
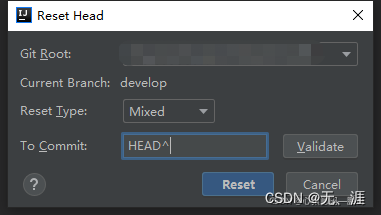
git 基本命令 reset 撤销commit https://blog.csdn.net/a704397849/article/details/135220091 idea 中 rest 撤销commit过程如下: Git -> Rest Head… 在To Commit中的HEAD后面加上^,点击Reset即可撤回最近一次的尚未push的commit Reset Type 有三…...

Vue Echarts 多折线图只有一条X轴(合并X轴数据并去重排序) - 附完整示例
echarts:一个基于 JavaScript 的开源可视化图表库。 目录 效果 一、介绍 1、官方文档:Apache ECharts 2、官方示例 二、准备工作 1、安装依赖包 2、示例版本 三、使用步骤 1、在单页面引入 echarts 2、指定容器并设置容器宽高 3、数据处理&am…...
WPF+Halcon 培训项目实战(6):目标匹配助手
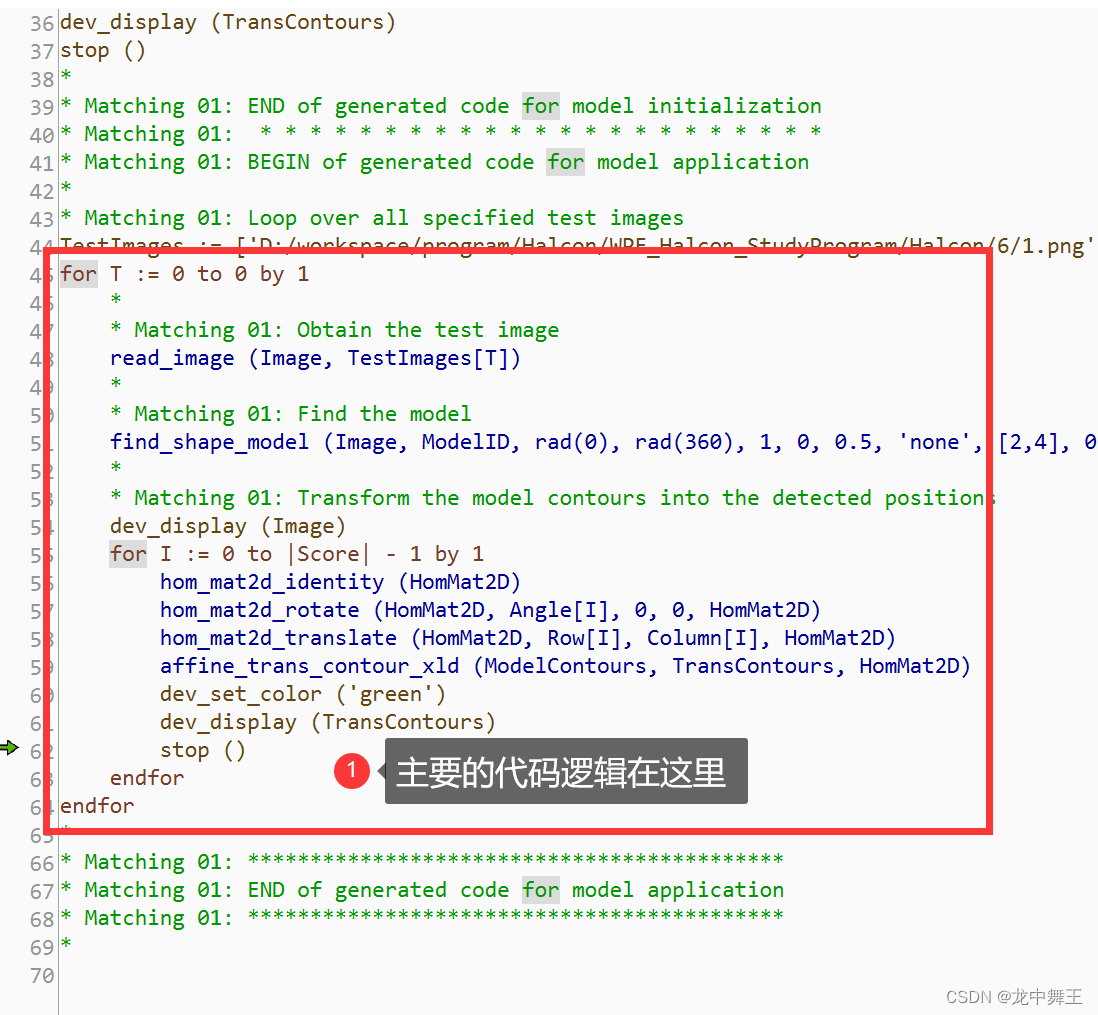
文章目录 前言相关链接项目专栏模板匹配助手简单使用金字塔级别参数自动选择应用插入代码 总结 前言 为了更好地去学习WPFHalcon,我决定去报个班学一下。原因无非是想换个工作。相关的教学视频来源于下方的Up主的提供的教程。这里只做笔记分享,想要源码…...

Linux管理LVM逻辑卷
目录 一、LVM逻辑卷介绍 1. 概述 2. LVM基本术语 2.1 PV(Physical Volume,物理卷) 2.2 VG (Volume Group,卷组) 2.3 LV (Logical Volume,逻辑卷) 3. 常用的磁盘命令 4. 查看系统信息的命…...

vue如何实现局部刷新?
应用场景: 比如你要切换tap栏实现刷新下面form表单等,相当于刷新页面。 如何使用如下: <div v-if"isReloadData"> 比如你想刷新那个位置就把 v-if"isReloadData"写到那个标签上 </div> 在data中定义刷新标…...

C语言,指针链表详解解说及代码示例
C语言,指针链表详解解说及代码示例 指针链表是一种常用的数据结构,用于存储和组织数据。它由一系列节点组成,每个节点包含数据和一个指向下一个节点的指针。通过这种方式,可以动态地添加、删除和访问节点,实现灵活的数…...
6、LLaVA
简介 LLaVA官网 LLaVA使用Vicuna(LLaMA-2)作为LLM f ϕ ( ⋅ ) f_\phi() fϕ(⋅),使用预训练的CLIP图像编码器 ViT-L/14 g ( X v ) g(X_v) g(Xv)。 输入图像 X v X_v Xv,首先获取feature Z v g ( X v ) Z_vg(X_v) Zvg(Xv)。考虑到最后一…...

SpringMVC核心处理流程梳理
1、处理流程图展示 当我拿出这张图,阁下又该如何应对呢?执行流程是不是一目了然了。【记住一句话:所有的注解都只是一个标签或者标记,最终都是反射找到具体方法上面的注解标记,然后找到类、属性、方法扩展自己想要的功…...

go 语言程序设计第2章--程序结构
2.1 名称 如果一个实体在函数中声明,它只在函数局部有效。如果声明在函数外,它将对包里面所有源文件可见。 实体第一个字母的大小写决定其可见性是否跨包。如果名称以大写字母开头,它是导出的,意味着它对包外是可见和可访问的。包…...
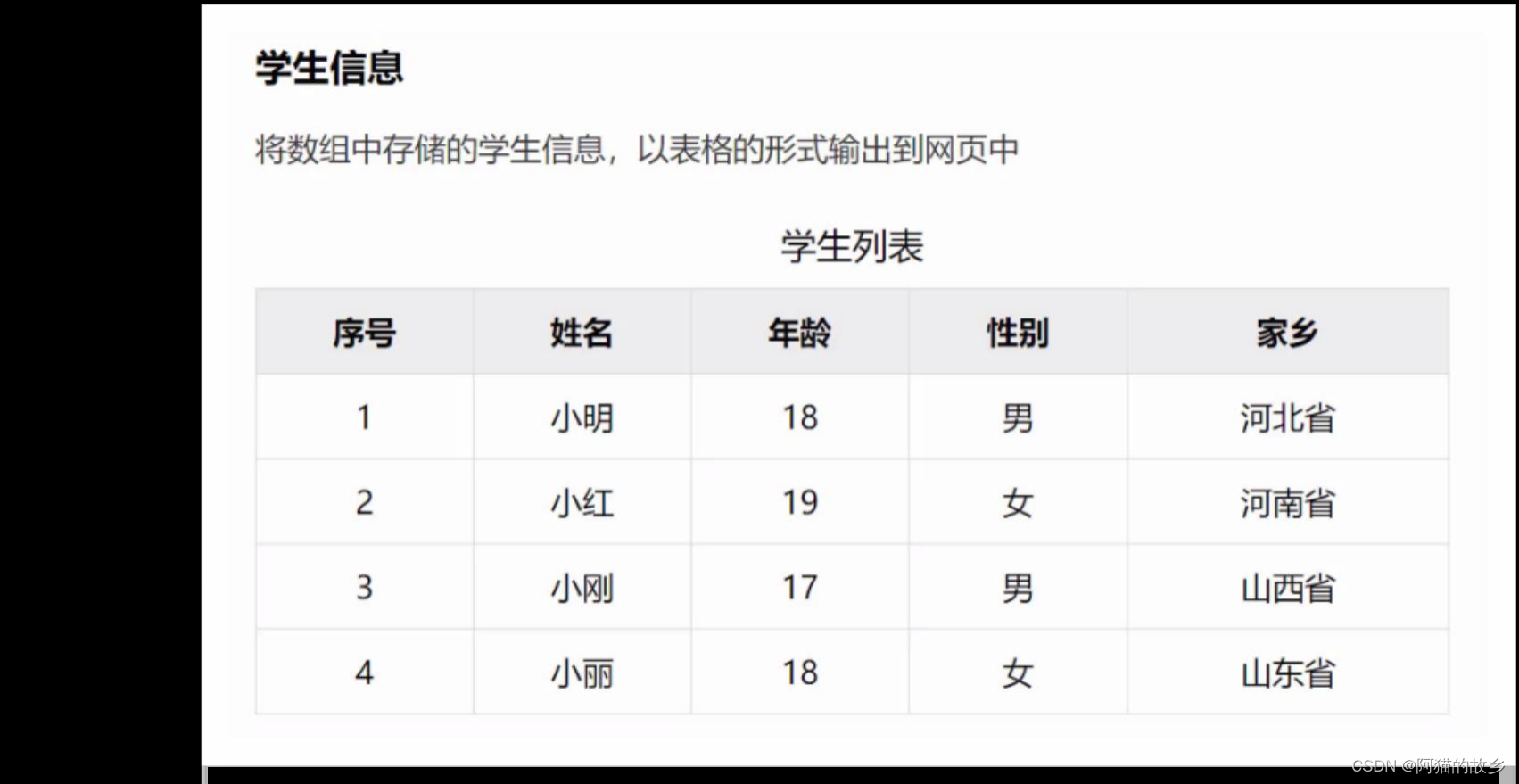
JavaScript基础知识点总结:从零开始学习JavaScript(五)
如果大家感感兴趣也可以去看: 🎉博客主页:阿猫的故乡 🎉系列专栏:JavaScript专题栏 🎉ajax专栏:ajax知识点 🎉欢迎关注:👍点赞🙌收藏✍️留言 学习…...

Intel FPGA 技术开放日
概要 时间:2023.11.14 全天 ( 9:00 - 16: 20) 地点:北京望京. 凯悦酒店 主题内容:分享交流了Intel FPGA 产品技术优势和落地实践方案。 会议的议程 开场致词: FPGA业务,是几年前intel收购而…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
