25- 卷积神经网络(CNN)原理 (TensorFlow系列) (深度学习)
知识要点
-
卷积神经网络的几个主要结构:
-
卷积层(Convolutions):
-
Valid :不填充,也就是最终大小为卷积后的大小.
-
Same:输出大小与原图大小一致,那么N 变成了N+2P. padding-零填充.
-
-
池化层(Subsampling), 主要对卷积层学习到的特征图进行亚采样处理:
-
最大池化:Max Pooling, 取窗口内的最大值作为输出
-
平均池化:Avg Pooling, 取窗口内的所有值的均值作为输出
-
-
全连接层(Full connection)
-
卷积层+激活层+池化层可以看成是CNN的特征学习/特征提取层,而学习到的特征(Feature Map)最终应用于模型任务,需要先对所有 Feature Map 进行扁平化.
-
-
激活函数
-
softmax, relu, selu, sigmoid
-
-
- filters , 卷积核, 必须是4维的tensor(卷积核的高度和宽度, 输入图片的通道数, 卷积核的个数)
- strides, 步长, 卷积核在图片的各个维度的移动步长, (1, 1, 1)
- padding, 0填充, 'valid'和'same', valid 表示不填充, same表示输入图片和输出图片的大小保持一致, (会自动计算)
- 显示卷积过程中的图像:
# 边缘检测
input_img = tf.constant(cat_gray.reshape(1, 456, 730, 1), dtype = tf.float32)
filters = tf.constant(np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]).reshape(3, 3, 1, 1), dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input = input_img, filters= filters, strides= strides, padding= 'SAME')
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(456, 730), cmap = 'gray')一 卷积神经网络(CNN)原理
1.1 卷积神经网络的组成
1.1.1 简介
-
卷积神经网络由一个或多个卷积层、池化层以及全连接层等组成。与其他深度学习结构相比,卷积神经网络在图像等方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他浅层或深度神经网络,卷积神经网络需要考量的参数更少,使之成为一种颇具吸引力的深度学习结构。
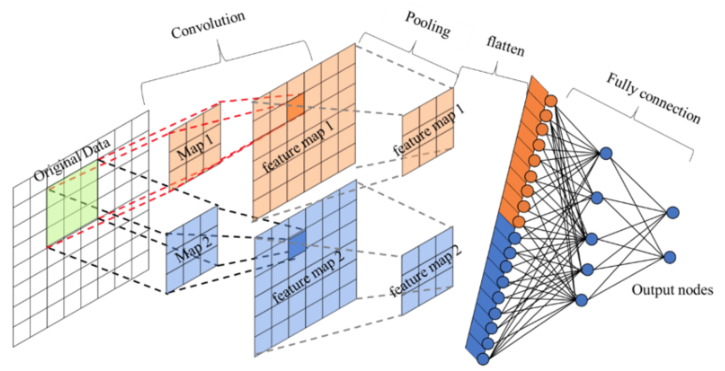
我们来看一下卷积网络的整体结构什么样子。
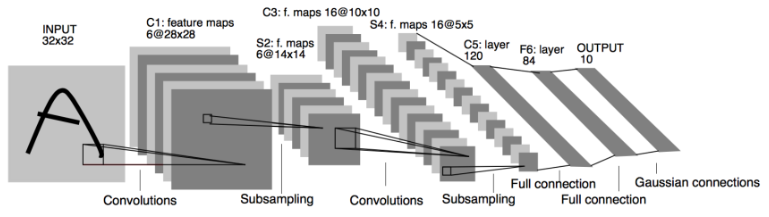
其中包含了几个主要结构
-
卷积层(Convolutions)
-
池化层(Subsampling)
-
全连接层(Full connection)
-
激活函数
1.1.2 卷积层
-
目的: 卷积运算的目的是提取输入的不同特征,某些卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网路能从低级特征中迭代提取更复杂的特征。
-
参数:
-
size: 卷积核/过滤器大小,选择有1 *1, 3* 3, 5 * 5
-
padding:零填充,Valid 与Same
-
stride: 步长,通常默认为1
-
-
计算公式

1.1.3 卷积运算过程
对于之前介绍的卷积运算过程,我们用一张动图来表示更好理解些。一下计算中,假设图片长宽相等,设为N, 一个步长, 3 X 3 卷积核运算。
假设是一张5 X 5 的单通道图片,通过使用3 X 3 大小的卷积核运算得到一个 3 X 3大小的运算结果(图片像素数值仅供参考)
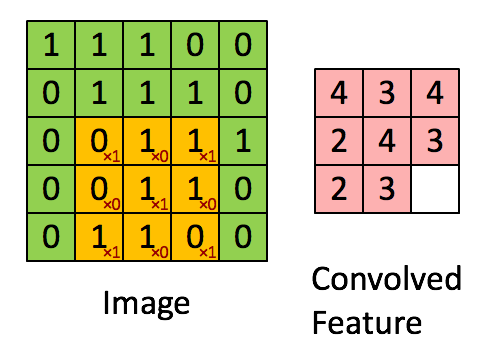
我们会发现进行卷积之后的图片变小了,假设N为图片大小,F为卷积核大小
相当于:
如果我们换一个卷积核大小或者加入很多层卷积之后,图像可能最后就变成了1 X 1 大小,这不是我们希望看到的结果。并且对于原始图片当中的边缘像素来说,只计算了一遍,二对于中间的像素会有很多次过滤器与之计算,这样导致对边缘信息的丢失。
缺点:
-
图像变小
-
边缘信息丢失
1.1.4 padding-零填充
零填充:在图片像素的最外层加上若干层0值,若一层,记做p =1。
-
为什么增加的是0?
因为0在权重乘积和运算中对最终结果不造成影响,也就避免了图片增加了额外的干扰信息。
这张图中,还是移动一个像素,并且外面增加了一层0。那么最终计算结果我们可以这样用公式来计算:, P为1,那么最终特征结果为5。实际上我们可以填充更多的像素,假设为2层,则
,这样得到的观察特征大小比之前图片大小还大。所以我们对于零填充会有一些选择,该填充多少?
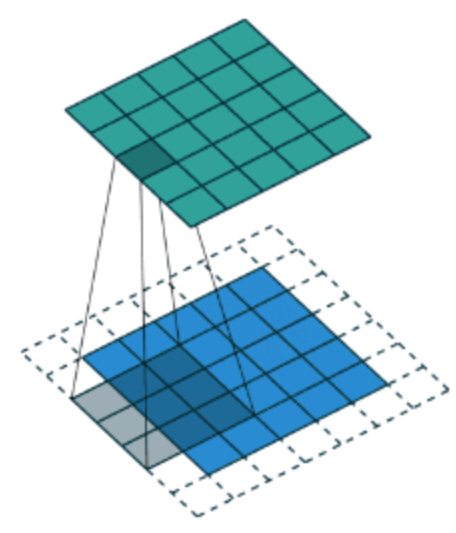
1.1.5 Valid and Same卷积
有两种形式,所以为了避免上述情况,大家选择都是Same这种填充卷积计算方式
-
Valid :不填充,也就是最终大小为:
-
Same:输出大小与原图大小一致,那么N 变成了N+2P:
那也就意味着,之前大小与之后的大小一样,得出下面的等式
所以当知道了卷积核的大小之后,就可以得出要填充多少层像素。
1.1.6 奇数维度的过滤器 (卷积核)
通过上面的式子,如果F不是奇数而是偶数个,那么最终计算结果不是一个整数,造成0.5,1.5.....这种情况,这样填充不均匀,所以也就是为什么卷积核默认都去使用奇数维度大小
-
1 *1,3* 3, 5 *5,7* 7
-
另一个解释角度
-
奇数维度的过滤器有中心,便于指出过滤器的位置
-
当然这个都是一些假设的原因,最终原因还是在F对于计算结果的影响。所以通常选择奇数维度的过滤器,是大家约定成俗的结果,可能也是基于大量实验奇数能得出更好的结果。
1.1.7 stride-步长
以上例子中我们看到的都是每次移动一个像素步长的结果,如果将这个步长修改为2,3,那结果如何?
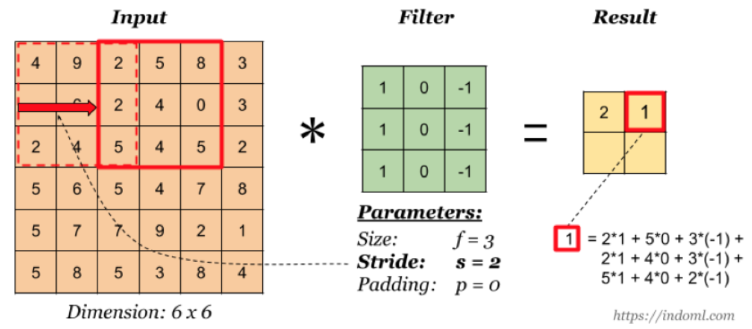
这样如果以原来的计算公式,那么结果:
但是移动2个像素才得出一个结果,所以公式变为: ,如果相除不是整数的时候,向下取整,为2。这里并没有加上零填充。
所以最终的公式就为:
- 对于输入图片大小为N,过滤器大小为F,步长为S,零填充为P:
1.2 多通道卷积
当输入有多个通道(channel)时(例如图片可以有 RGB 三个通道),卷积核需要拥有相同的channel 数, 每个卷积核 channel 与输入层的对应 channel 进行卷积,将每个 channel 的卷积结果按位相加得到最终的 Feature Map。
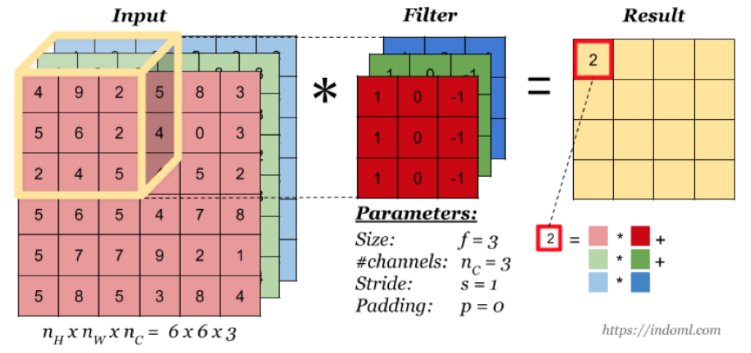
1.2.1 多卷积核
当有多个卷积核时,可以学习到多种不同的特征,对应产生包含多个 channel 的 Feature Map, 例如上图有两个 filter,所以 output 有两个 channel。这里的多少个卷积核也可理解为多少个神经元。相当于我们把多个功能的卷积核的计算结果放在一起,比如水平边缘检测和垂直边缘检测器。
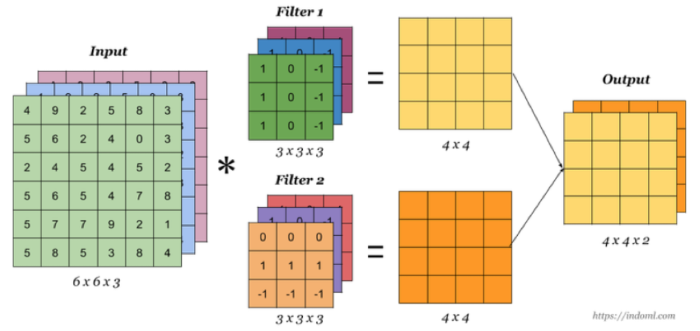
1.2.2 卷积总结
我们来通过一个例子看一下结算结果,以及参数的计算
-
假设我们有10 个Filter,每个Filter3 X 3 X 3(计算RGB图片),并且只有一层卷积,那么参数有多少?
计算:每个Filter参数个数为: 个权重参数,总共28 * 10 = 280个参数,即使图片任意大小,我们这层的参数也就这么多。
-
假设一张200 *200* 3的图片,进行刚才的Filter,步长为1,最终为了保证最后输出的大小为200 * 200,需要设置多大的零填充
1.2.3 设计单个卷积Filter的计算公式
假设神经网络某层l的输入:
-
inputs:
-
卷积层参数设置:
-
:filter的大小
-
:padding的大小
-
:stride大小
-
:filter的总数量
-
-
outputs:
所以通用的表示每一层:
-
每个Filter:
-
权重Weights:
-
应用激活函数Activations:
-
偏差bias:
,通常会用4维度来表示
之前的式子我们就可以简化成,假设多个样本编程向量的形式:
1.3 池化层(Pooling)
池化层主要对卷积层学习到的特征图进行亚采样(subsampling)处理,主要由两种:
-
最大池化:Max Pooling, 取窗口内的最大值作为输出
-
平均池化:Avg Pooling, 取窗口内的所有值的均值作为输出
意义在于:
-
降低了后续网络层的输入维度,缩减模型大小,提高计算速度
-
提高了Feature Map 的鲁棒性,防止过拟合
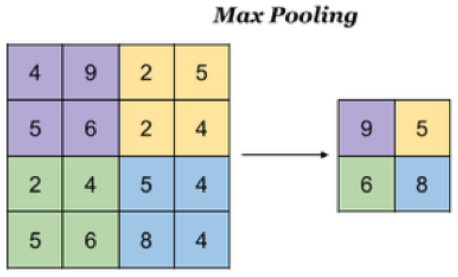
对于一个输入的图片,我们使用一个区域大小为2 *2,步长为2的参数进行求最大值操作。同样池化也有一组参数,f, s,得到2* 2的大小。当然如果我们调整这个超参数,比如说3 * 3,那么结果就不一样了,通常选择默认都是f = 2 * 2, s = 2
池化超参数特点:不需要进行学习,不像卷积通过梯度下降进行更新。
如果是平均池化则:
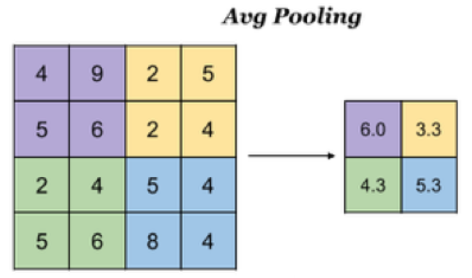
1.4 全连接层
卷积层+激活层+池化层可以看成是CNN的特征学习/特征提取层,而学习到的特征(Feature Map)最终应用于模型任务(分类、回归):
-
先对所有 Feature Map 进行扁平化(flatten, 即 reshape 成 1 x N 向量)
-
再接一个或多个全连接层,进行模型学习
二 图像数据与边缘检测
2.1 为什么需要卷积神经网络
在计算机视觉领域,通常要做的就是指用机器程序替代人眼对目标图像进行识别等。那么神经网络也好还是卷积神经网络其实都是上个世纪就有的算法,只是近些年来电脑的计算能力已非当年的那种计算水平,同时现在的训练数据很多,于是神经网络的相关算法又重新流行起来,因此卷积神经网络也一样流行。
-
1974年,Paul Werbos提出了误差反向传导来训练人工神经网络,使得训练多层神经网络成为可能。
-
1979年,Kunihiko Fukushima(福岛邦彦),提出了Neocognitron, 卷积、池化的概念基本形成。
-
1986年,Geoffrey Hinton与人合著了一篇论文:Learning representations by back-propagation errors。
-
1989年,Yann LeCun提出了一种用反向传导进行更新的卷积神经网络,称为LeNet。
-
1998年,Yann LeCun改进了原来的卷积网络,LeNet-5。
2.2 图像特征数量对神经网络效果压力
假设下图是一图片大小为28 * 28 的黑白图片时候,每一个像素点只有一个值(单通道)。那么总的数值个数为 784个特征。

那现在这张图片是彩色的,那么彩色图片由RGB三通道组成,也就意味着总的数值有28 28 3 = 2352个值。

从上面我们得到一张图片的输入是2352个特征值,即神经网路当中与若干个神经元连接,假设第一个隐层是10个神经元,那么也就是23520个权重参数。
如果图片再大一些呢,假设图片为1000 *1000* 3,那么总共有3百万数值,同样接入10个神经元,那么就是3千万个权重参数。这样的参数大小,神经网络参数更新需要大量的计算不说,也很难达到更好的效果,大家就不倾向于使用多层神经网络了。
所以就有了卷积神经网络的流行,那么卷积神经网络为什么大家会选择它。那么先来介绍感受野以及边缘检测的概念。
2.3 感受野
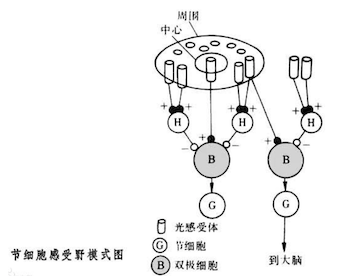
1962年Hubel和Wiesel通过对猫视觉皮层细胞的研究,提出了感受野(receptive field)的概念, Fukushima基于感受野概念提出的神经认知机(neocognitron)可以看作是卷积神经网络的第一个实现网络。
单个感受器与许多感觉神经纤维相联系,感觉信息是通过许多感受神经纤维发放总和性的空间与时间类型不同的冲动,相当于经过编码来传递。
2.4 边缘检测
为了能够用更少的参数,检测出更多的信息,基于上面的感受野思想。通常神经网络需要检测出物体最明显的垂直和水平边缘来区分物体。比如
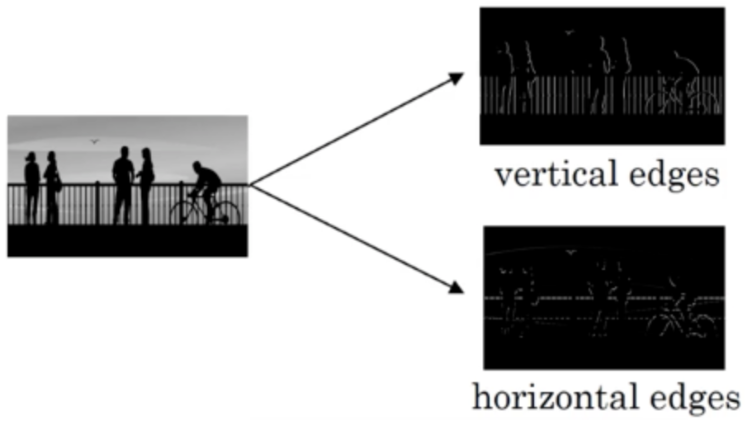
看一个列子,一个 6×6的图像卷积与一个3×3的过滤器(Filter or kenel)进行卷积运算(符号为 *),* 也可能是矩阵乘法所以通常特别指定是卷积的时候代表卷积意思。
-
相当于将 Filter 放在Image 上,从左到右、从上到下地(默认一个像素)移动过整个Image,分别计算 ImageImage 被 Filter 盖住的部分与 Filter的逐元素乘积的和
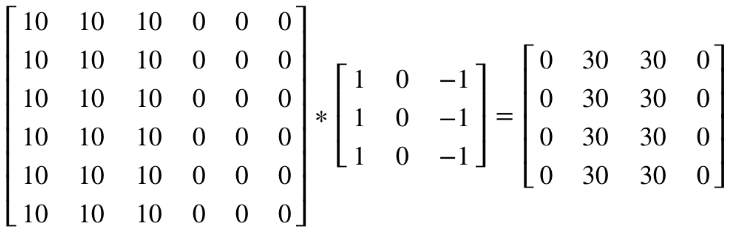
在这个6×6 的图像中,左边一半像素的值全是 10,右边一半像素的值全是 0,中间是一条非常明显的垂直边缘。这个图像与过滤器卷积的结果中,中间两列的值都是 30,两边两列的值都是 0,即检测到了原 6×66×6 图像中的垂直边缘。
注:虽然看上去非常粗,是因为我们的图像太小,只有5个像素长、宽,所以最终得到结果看到的是两个像素位置,如果在一个500 x 500的图当中,就是一个竖直的边缘了。

随着深度学习的发展,我们需要检测更复杂的图像中的边缘,与其使用由人手工设计的过滤器,还可以将过滤器中的数值作为参数,通过反向传播来学习得到。算法可以根据实际数据来选择合适的检测目标,无论是检测水平边缘、垂直边缘还是其他角度的边缘,并习得图像的低层特征。
三 图片卷积实操
3.1 均值滤波
# 登月图
moon = plt.imread('./moonlanding.png')
print(moon.shape) # (474, 630)
plt.figure(figsize=(10, 8))
plt.imshow(moon, cmap = 'gray')
# 均值滤波 # 平滑处理, 用卷积直接扫描
input_img = tf.constant(moon.reshape(1, 474, 630, 1), dtype = tf.float32)
filters = tf.constant(np.array([[1/9, 1/9, 1/9], [1/9, 1/9, 1/9], [1/9, 1/9, 1/9]]).reshape(3, 3, 1, 1),dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input = input_img, filters= filters, strides= strides, padding= 'SAME')
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(474, 630), cmap = 'gray')
# 高斯滤波 # 平滑处理, 用卷积直接扫描
input_img = tf.constant(moon.reshape(1, 474, 630, 1), dtype = tf.float32)
filters = tf.constant(np.array([[1/9, 2/9, 1/9], [2/9, 3/9, 2/9], [1/9, 2/9, 1/9]]).reshape(3, 3, 1, 1), dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input = input_img, filters= filters, strides= strides, padding= 'SAME')
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(474, 630), cmap = 'gray')
# 均值滤波 # 平滑处理, 用卷积直接扫描
input_img = tf.constant(moon.reshape(1, 474, 630, 1), dtype = tf.float32)
filters = tf.constant(np.array([[9/9, 9/9, 9/9, 9/9, 9/9], [9/9, 9/9, 9/9, 9/9, 9/9],[9/9, 9/9, 9/9, 9/9, 9/9], [9/9, 9/9, 9/9, 9/9, 9/9],[9/9, 9/9, 9/9, 9/9, 9/9]]).reshape(5, 5, 1, 1), dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input = input_img, filters= filters, strides= strides, padding= 'SAME')
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(474, 630), cmap = 'gray')
3.2 边缘检测
cat = plt.imread('./cat.jpg')
plt.figure(figsize= (12, 8))
plt.imshow(cat)
# 把猫变成黑白图片
cat_gray = cat.mean(axis = 2)
plt.figure(figsize= (12, 8))
plt.imshow(cat_gray, cmap = 'gray')
# 边缘检测
input_img = tf.constant(cat_gray.reshape(1, 456, 730, 1), dtype = tf.float32)
filters = tf.constant(np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]).reshape(3, 3, 1, 1), dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input = input_img, filters= filters, strides= strides, padding= 'SAME')
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(456, 730), cmap = 'gray')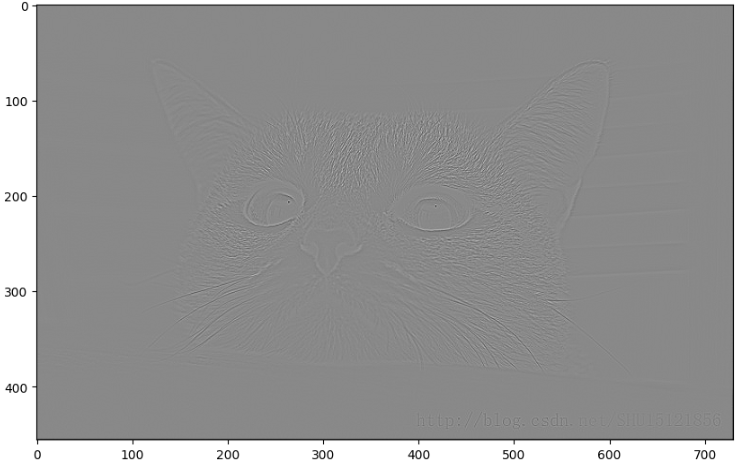
3.3 锐化效果
# 边缘检测
input_img = tf.constant(cat_gray.reshape(1, 456, 730, 1), dtype = tf.float32)
filters = tf.constant(np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]]).reshape(3, 3, 1, 1), dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input = input_img, filters= filters, strides= strides, padding= 'SAME')
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(456, 730), cmap = 'gray')
europe = plt.imread('./欧式.jpg')
plt.figure(figsize=(10, 8))
plt.imshow(europe)
print(europe.shape) # (582, 1024, 3)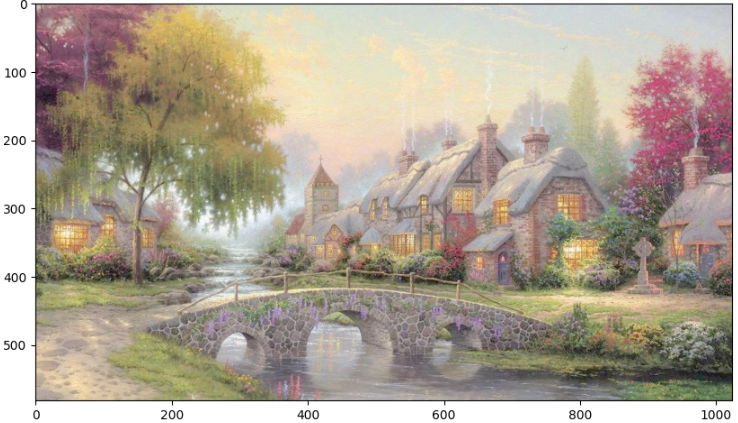
# 彩色图片
# 把每个通道当做一张图 # transpose通过索引调换维度位置
input_img = tf.constant(europe.reshape(1, 582, 1024, 3).transpose([3, 1, 2, 0]), dtype = tf.float32)
filters = tf.constant(np.array([[1/9, 1/9, 1/9], [1/9, 1/9, 1/9], [1/9, 1/9, 1/9]]).reshape(3, 3, 1, 1), dtype = tf.float32)
strides = [1, 1, 1, 1]
conv2d = tf.nn.conv2d(input = input_img, filters= filters, strides= strides, padding= 'SAME')
print(conv2d.shape) # (3, 582, 1024, 1)
plt.figure(figsize= (10, 8))
plt.imshow(conv2d.numpy().reshape(3, 582, 1024).transpose([1, 2, 0])/255)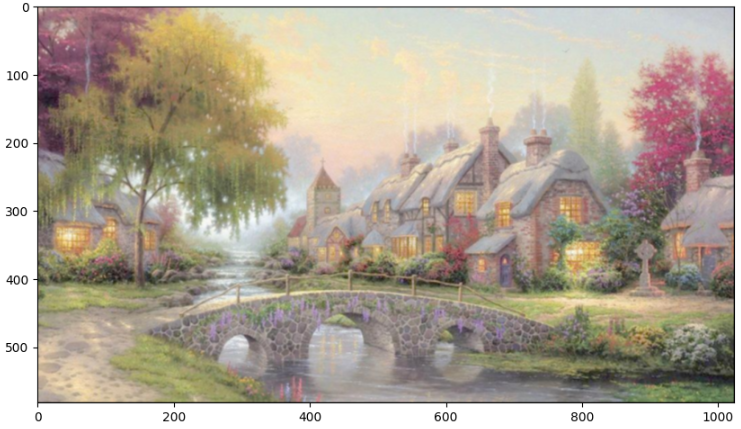
相关文章:

25- 卷积神经网络(CNN)原理 (TensorFlow系列) (深度学习)
知识要点 卷积神经网络的几个主要结构: 卷积层(Convolutions): Valid :不填充,也就是最终大小为卷积后的大小. Same:输出大小与原图大小一致,那么N 变成了N2P. padding-零填充. 池化层(Subsampli…...

把数组里面数值排成最小的数
问题描述:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。例如输入数组{12, 567},则输出这两个能排成的最小数字12567。请给出解决问题的算法,并证明该算法。 思路:先将…...
云his系统源码 SaaS应用 基于Angular+Nginx+Java+Spring开发
云his系统源码 SaaS应用 功能易扩 统一对外接口管理 一、系统概述: 本套云HIS系统采用主流成熟技术开发,软件结构简洁、代码规范易阅读,SaaS应用,全浏览器访问前后端分离,多服务协同,服务可拆分ÿ…...

小红书场景营销怎么做?场景营销主要模式有哪些
小红书作为新兴媒体领域的佼佼者,凭借着生动,直观,代入感等元素的分享推荐收揽了巨额的流量。但是,随着时代的脚步逐渐加快,发展和变革随之涌来,传统的营销已经无法满足。所以场景营销就出现了。今天就来和…...

c++基础——数组
数组数组是存放相同类型对象的容器,数组中存放的对象没有名字,而是要通过其所在的位置访问。数组的大小是固定的,不能随意改变数组的长度。定义数组数组的声明形如 a[b],其中,a 是数组的名字,b 是数组中元素…...
odoo15 登录界面的标题自定义
odoo15 登录界面的标题自定义 原代码中查询:<title>Odoo<title> <html> <head><meta http-equiv="content-type" content="text/html; charset=utf-8" /><title>Odoo</title><link rel="shortcut icon…...

【内网服务通过跳板机和公网通信】花生壳内网穿透+Nginx内网转发+mqtt服务搭建
问题:服务不能暴露公网 客户的主机不能连外网,服务MQTT服务部署在内网。记做:p1 (computer 1)堡垒机(跳板机)可以连外网,内网IP 和 MQTT服务在同一个网段。记做:p2 (computer 2)对他人而言&…...

【多线程常见面试题】
谈谈 volatile关键字的用法? volatile能够保证内存可见性,强制从主内存中读取数据,此时如果有其他线程修改被volatile修饰的变量,可以第一时间读取到最新的值 Java多线程是如何实现数据共享的? JVM把内存分成了这几个区域: 方法区,堆区,栈区,程序计数器; 其中堆区…...

深度剖析指针(下)——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容还是我们的指针呀,上两篇博客我们基本上已经把知识点过了一遍,这篇博客就让小雅兰来带大家看一些和指针有关的题目吧,现在,就让我们进入指针的世界吧 复习: 数组和…...

爬虫与反爬虫技术简介
互联网的大数据时代的来临,网络爬虫也成了互联网中一个重要行业,它是一种自动获取网页数据信息的爬虫程序,是网站搜索引擎的重要组成部分。通过爬虫,可以获取自己想要的相关数据信息,让爬虫协助自己的工作,…...

Pag的2D渲染执行流程
Pag的渲染 背景 根据Pag文章里面说的,Pag之前长时间使用的Skia库作为底层渲染引擎。但由于Skia库体积过大,为了保证通用型(比如兼容CPU渲染)做了很多额外的事情。所以Pag的工程师们自己实现了一套2D图形框架替换掉Skiaÿ…...

k8s 概念说明,k8s面试题
什么是Kubernetes? Kubernetes是一种开源容器编排系统,可自动化应用程序的部署、扩展和管理。 Kubernetes 中的 Master 组件有哪些? Kubernetes 中的 Master 组件包括 API Server、etcd、Scheduler 和 Controller Manager。 Kubernetes 中的…...

Docker--(四)--搭建私有仓库(registry、harbor)
私有仓库----registry官方提供registry仓库管理(推送、删除、下载)私有仓库----harbor私有镜像仓库1.私有仓库----registry官方提供 Docker hub官方已提供容器镜像registry,用于搭建私有仓库 1.1 镜像拉取、运行、查看信息、测试 (一) 拉取镜像 # dock…...

Invalid <url-pattern> [sso.action] in filter mapping
Tomcat 8.5.86版本启动web项目报错Caused by: java.lang.IllegalArgumentException: Invalid <url-pattern> [sso.action] in filter mapping 查看项目的web.xml文件相关片段 <filter-mapping><filter-name>SSOFilter</filter-name><url-pattern&g…...

【11】linux命令每日分享——useradd添加用户
大家好,这里是sdust-vrlab,Linux是一种免费使用和自由传播的类UNIX操作系统,Linux的基本思想有两点:一切都是文件;每个文件都有确定的用途;linux涉及到IT行业的方方面面,在我们日常的学习中&…...
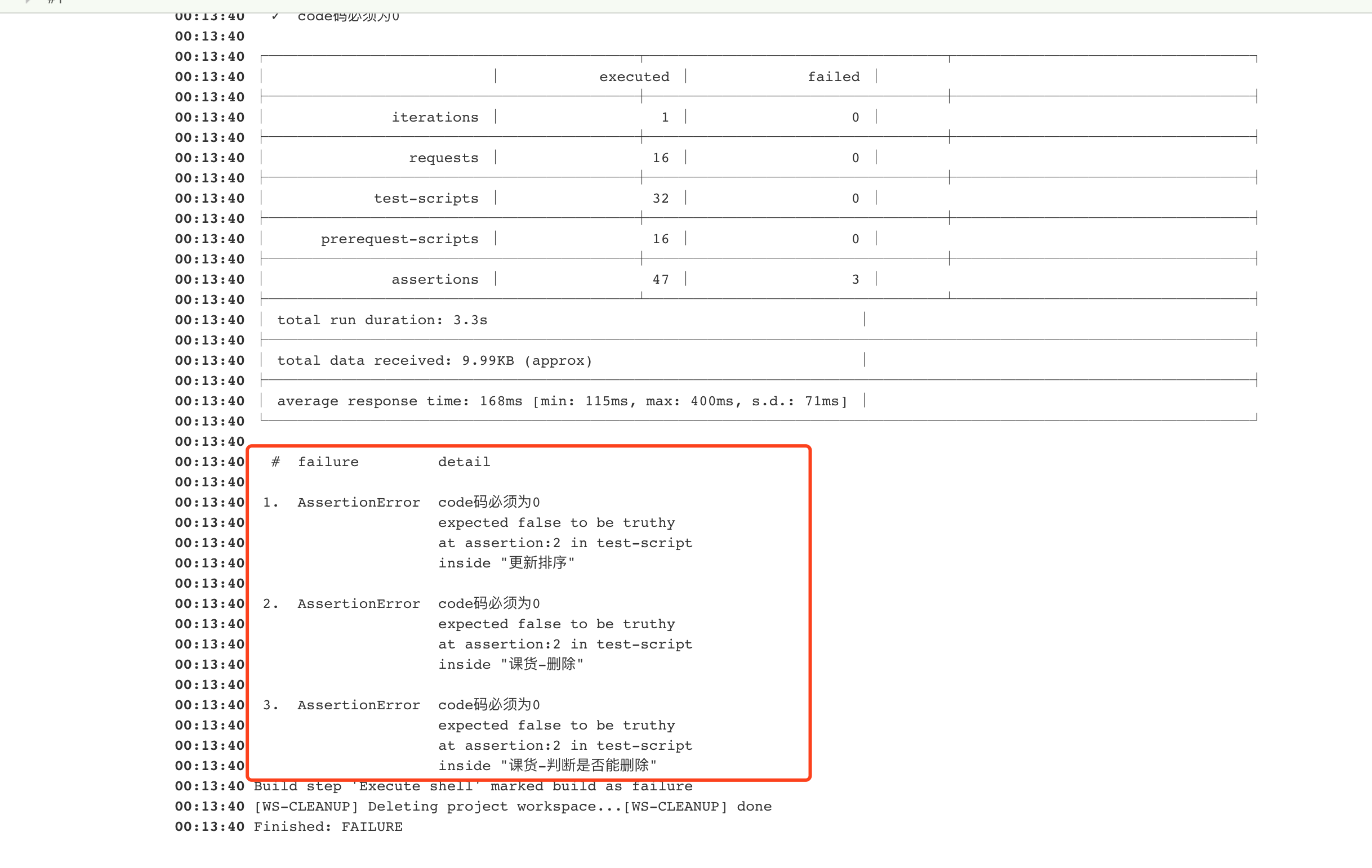
Newman+Jenkins实现接口自动化测试
一、是什么Newman Newman就是纽曼手机这个经典牌子,哈哈,开玩笑啦。。。别当真,简单地说Newman就是命令行版的Postman,查看官网地址。 Newman可以使用Postman导出的collection文件直接在命令行运行,把Postman界面化运…...

MySQL:事务+@Transactional注解
事务 本章从了解为什么需要事务到讲述事务的四大特性和概念,最后讲述MySQL中的事务使用语法以及一些需要注意的性质。 再额外讲述一点Springboot中Transactional注解的使用。 1.为什么需要事务? 我们以用户转账为例,假设用户A和用户B的银行账…...
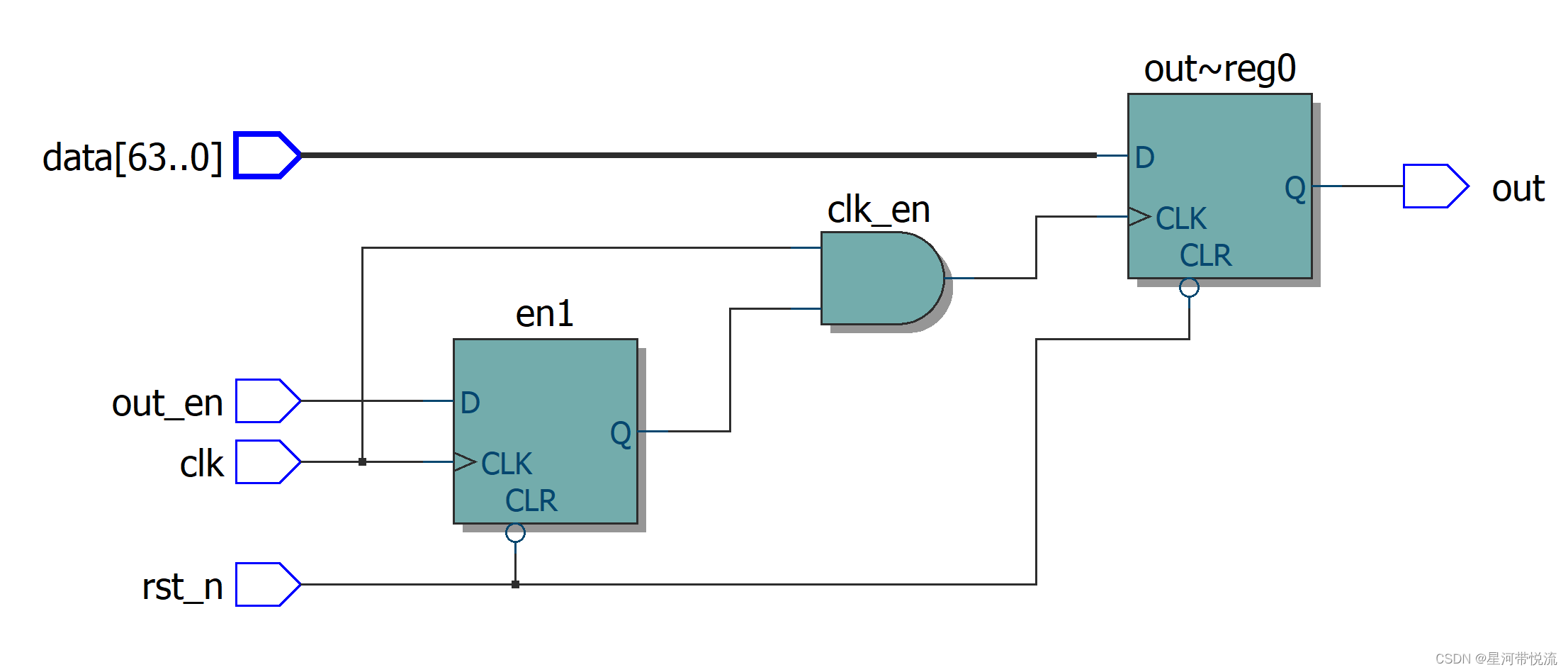
数字IC手撕代码--低功耗设计 Clock Gating
背景介绍芯片功耗组成中,有高达 40%甚至更多是由时钟树消耗掉的。这个结果的原因也很直观,因 为这些时钟树在系统中具有最高的切换频率,而且有很多时钟 buffer,而且为了最小化时钟 延时,它们通常具有很高的驱动强度。 …...

易基因|m6A RNA甲基化研究的数据挖掘思路:干货系列
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。关于m6A甲基化研究思路(1)整体把握m6A甲基化图谱特征:m6A peak数量变化、m6A修饰基因数量变化、单个基因m6A peak数量分析、m6A peak在基因元件上的分布…...

【微信小程序】-- 页面配置(十八)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
