[嵌入式专栏](FOC - SVPWM扇区计算Part1)
文章目录
- 1 . 概要
- 2 . 扇区计算
- 2.1 扇区Ⅰ计算
- 2.2 扇区Ⅱ计算
- 2.3 扇区Ⅲ计算
- 3 . 小结
【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485
1 . 概要
经过扇区判断后,就知道在哪个扇区进行输出了
【Q】但是每个扇区分别输出怎样的结果呢?
【A】这篇博文详述了这个意义
2 . 扇区计算
这里一开始先把六个扇区的TxTy结果列出来,方便看到文章开头记住扇区关系,后面内容对每个扇区有 详细推导过程
| 扇区 | Tx | Ty |
|---|---|---|
| Ⅰ | 3 T s U d c ( 3 2 U α − 1 2 U β ) \frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α-\frac 1 2Uβ ) Udc3Ts(23Uα−21Uβ) | 3 T s U d c U β \frac {\sqrt3 T_s}{U_{dc}}Uβ Udc3TsUβ |
| Ⅱ | 3 T s U d c ( − 3 2 U α + 1 2 U β ) \frac {\sqrt3 T_s}{U_{dc}}(-\frac {\sqrt3}2U_α+\frac 1 2Uβ ) Udc3Ts(−23Uα+21Uβ) | 3 T s U d c ( 3 2 U α + 1 2 U β ) \frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α+\frac 1 2Uβ ) Udc3Ts(23Uα+21Uβ) |
| Ⅲ | 3 T s U d c U β \frac {\sqrt3 T_s}{U_{dc}}Uβ Udc3TsUβ | − 3 T s U d c ( 3 2 U α + 1 2 U β ) -\frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α+\frac 1 2Uβ ) −Udc3Ts(23Uα+21Uβ) |
| Ⅳ | − 3 T s U d c U β -\frac {\sqrt3 T_s}{U_{dc}}Uβ −Udc3TsUβ | 3 T s U d c ( − 3 2 U α + 1 2 U β ) \frac {\sqrt3 T_s}{U_{dc}}(- \frac {\sqrt3}2U_α+\frac 1 2Uβ ) Udc3Ts(−23Uα+21Uβ) |
| Ⅴ | − 3 T s U d c ( 3 2 U α + 1 2 U β ) -\frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α+\frac 1 2Uβ ) −Udc3Ts(23Uα+21Uβ) | − 3 T s U d c ( − 3 2 U α + 1 2 U β ) -\frac {\sqrt3 T_s}{U_{dc}}( -\frac {\sqrt3}2U_α+\frac 1 2Uβ ) −Udc3Ts(−23Uα+21Uβ) |
| Ⅵ | 3 T s U d c ( 3 2 U α + 1 2 U β ) \frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α+\frac 1 2Uβ ) Udc3Ts(23Uα+21Uβ) | − 3 T s U d c U β -\frac {\sqrt3 T_s}{U_{dc}}Uβ −Udc3TsUβ |
>这里讲一下扇区计算的概念
【Q】前面计算了许多步骤最终把UαUβ送进SVPWM,那么怎么把UαUβ与SVPWM产生关联?
【A】答案是基于之前相电压合成关系代入
U α = U m c o s θ U_α = U_mcosθ Uα=Umcosθ
U β = U m s i n θ U_β = U_msinθ Uβ=Umsinθ
而 U m = 2 3 U d c U_m = \frac 2 3 U_{dc} Um=32Udc, 为什么是 2 3 U d c \frac 2 3U_{dc} 32Udc因为在SVPWM控制中,硬件的三组开关管里每一组时时刻刻都在开关状态,而形成回路中最多两路进,一路出,因此同一时刻相对 U d c U_{dc} Udc最多用到了 2 3 \frac 2 3 32

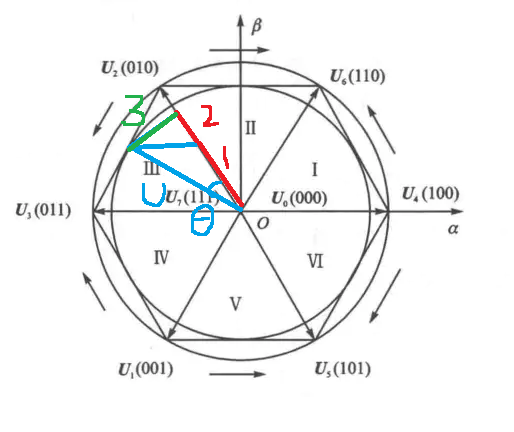
接下来如上图矢量圆所示,扇区Ⅰ, Ⅱ, Ⅲ, Ⅳ, Ⅴ, Ⅵ,矢量分别为U4 (100),U6 (110),U2 (010),U3 (011),U1 (001),U5 (101)
另外图中的α和β就是上述描述的UαUβ。
我们想要在这个 矢量圆 里输出N个不同大小,方向的矢量从而来控制电机力矩,但是我们只有六个基本矢量U4-U6-U2-U3-U1-U5,那怎么输出我们想要的矢量?这里我们只要基于六个基本矢量进行合成就可以了,具体根据每个扇区相邻的两个基本矢量进行合成,以下开始对每个扇区计算合成矢量。

这里以扇区一举例,如图所示把合成的矢量U设为 U o u t U_{out} Uout目标矢量,之前提到了
U α = U m c o s θ U_α = U_mcosθ Uα=Umcosθ
U β = U m s i n θ U_β = U_msinθ Uβ=Umsinθ
那么这里的 U m Um Um就是我们 U r e f U_{ref} Uref了
【Q】接下来分析 U m c o s θ = U_mcosθ = Umcosθ=? U m s i n θ = U_msinθ = Umsinθ=?
【A】根据上图标注 :
-
U m c o s θ U_mcosθ Umcosθ 为 红线1+红线2,其中红线1可以由U4这个矢量得到,红线2为U6经过cos60°可以得到,这里为什么要分为红线1与红线2,直接cosθ不就可以直接由U4矢量输出完成了吗,答案是因为要考虑后面 U m s i n θ U_msinθ Umsinθ的计算, U m s i n θ U_msinθ Umsinθ以图中加辅助线,可以通过sin60°U6得到 U m s i n θ U_msinθ Umsinθ的结果。
-
U m s i n θ U_msinθ Umsinθ 为 绿线,刚刚描述了这些线段的意义,以及图中加辅助线的意义,因此通过sin60°U6可以得到 U m s i n θ U_msinθ Umsinθ的结果。
【Q】我们芯片可以输出PWM高分辨率控制开关管,那么怎么把PWM与上面的公式逻辑结合起来?
【A】上面可以100, 110, 010, 011, 001, 101这六个组合分别对应了三组开关管的状态,“1”为上管开启,下管关闭,“0”为下管开启,上管关闭,上下管为互补状态,一个总周期 T s = T x + T y + T n T_s=T_x+T_y+T_n Ts=Tx+Ty+Tn 组成,这里 T x T y T_xT_y TxTy为对应矢量状态PWM输出, T n Tn Tn为不输出的周期,既然TxTy跟基本矢量产生联系,而UαUβ也跟基本矢量产生联系,那么TxTy就能跟UαUβ产生联系,这里也正式进入了SVPWM的计算联系点,接下来把六个矢量状态列出对应PWM(Tx,Ty)对应关系,这里的关系是人为设定的。
| Tx | Ty |
|---|---|
| U4(100) | U6(110) |
| U2(010) | U3(011) |
| U1(001) | U5(101) |
【Q】矢量的大小怎么确定?
【A】芯片输出的PWM来控制这些状态的占空比就可以实现矢量中的大小
【Q】矢量的方向怎么确定?
【A】这时候就要结合两个矢量的大小来“拉动”输出目标矢量,就像拔河比赛一样,两边谁拉的力多一点,绳子中间就往哪边靠,这里的 “绳子中间“ 就是 矢量合成
搞懂以上逻辑后,就可以计算出 目标矢量 了,而SVPWM之所以成为SVPWM就是因为芯片输出PWM来控制基本矢量状态,从而合成出“空间目标矢量 U o u t U_{out} Uout”。
2.1 扇区Ⅰ计算

根据上图解析出以下公式 :
U α = U o u t c o s θ = 2 3 U d c ∗ T x T s + 2 3 U d c ∗ T y T s ∗ c o s 60 ° U_α = U_{out}cosθ = \frac23U_{dc}*\frac {T_x} {T_s}+\frac23U_{dc}*\frac {T_y} {T_s}*cos60° Uα=Uoutcosθ=32Udc∗TsTx+32Udc∗TsTy∗cos60°
U β = U o u t s i n θ = 2 3 U d c ∗ T y T s ∗ s i n 60 ° U_β = U_{out}sinθ = \frac23U_{dc}*\frac {T_y} {T_s} * sin60° Uβ=Uoutsinθ=32Udc∗TsTy∗sin60°
可以看出Uα有涉及了Tx与Ty,而Uβ只有Ty,因此我们先求解Uβ中的Ty再代入Uα从而把Tx也求解出来
1. 解析扇区Ⅰ的 T y T_y Ty
U β = U o u t s i n θ = 2 3 U d c ∗ T y T s ∗ s i n 60 ° U_β = U_{out}sinθ = \frac23U_{dc}*\frac {T_y} {T_s} * sin60° Uβ=Uoutsinθ=32Udc∗TsTy∗sin60°
U β = 2 3 U d c ∗ T y T s ∗ 3 2 U_β = \frac23U_{dc}*\frac {T_y} {T_s} * \frac {\sqrt3}2 Uβ=32Udc∗TsTy∗23
U β = 3 3 U d c ∗ T y T s U_β = \frac {\sqrt3}3U_{dc}*\frac {T_y} {T_s} Uβ=33Udc∗TsTy
U β = 1 3 U d c ∗ T y T s U_β = \frac 1{\sqrt3}U_{dc}*\frac {T_y} {T_s} Uβ=31Udc∗TsTy
T y = 3 T s U d c U β T_y = \frac {\sqrt3 T_s}{U_{dc}}U_β Ty=Udc3TsUβ
2. 解析扇区Ⅰ的 T x T_x Tx
U α = U o u t c o s θ = 2 3 U d c ∗ T x T s + 2 3 U d c ∗ T y T s ∗ c o s 60 ° U_α = U_{out}cosθ = \frac23U_{dc}*\frac {T_x} {T_s}+\frac23U_{dc}*\frac {T_y} {T_s}*cos60° Uα=Uoutcosθ=32Udc∗TsTx+32Udc∗TsTy∗cos60°
U α = 2 3 U d c ∗ T x T s + 2 3 U d c ∗ T y T s ∗ 1 2 U_α = \frac23U_{dc}*\frac {T_x} {T_s}+\frac23U_{dc}*\frac {T_y} {T_s}*\frac 1 2 Uα=32Udc∗TsTx+32Udc∗TsTy∗21
U α = 2 3 U d c 1 T s ( T x + T y 1 2 ) U_α = \frac23U_{dc}\frac1{T_s}(T_x+T_y\frac12) Uα=32UdcTs1(Tx+Ty21)
T x = U α T s U d c 3 2 − T y 1 2 T_x= \frac {U_αT_s}{U_{dc}} \frac 3 2-T_y\frac12 Tx=UdcUαTs23−Ty21
T x = U α T s U d c 3 2 − 3 T s U d c U β 1 2 T_x= \frac {U_αT_s}{U_{dc}} \frac 3 2-\frac {\sqrt3 T_s}{U_{dc}}U_β\frac12 Tx=UdcUαTs23−Udc3TsUβ21
T x = U α T s 3 − 3 T s U β U d c 2 T_x= \frac { U_αT_s3-\sqrt3T_sU_β } {U_{dc}2} Tx=Udc2UαTs3−3TsUβ
T x = 3 T s ( U α 3 − U β ) U d c 2 T_x= \frac { \sqrt3T_s(U_α\sqrt3-U_β) } {U_{dc}2} Tx=Udc23Ts(Uα3−Uβ)
T x = 3 T s U d c ( 3 2 U α − 1 2 U β ) T_x= \frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α-\frac 1 2U_β ) Tx=Udc3Ts(23Uα−21Uβ)
2.2 扇区Ⅱ计算

根据上图解析出以下公式 :
U o u t c o s ( θ − 60 ° ) = 2 3 U d c ∗ T y T s + 2 3 U d c ∗ T x T s ∗ c o s 60 ° U_{out}cos(θ-60°) = \frac23U_{dc}*\frac {T_y} {T_s}+\frac23U_{dc}*\frac {T_x} {T_s}*cos60° Uoutcos(θ−60°)=32Udc∗TsTy+32Udc∗TsTx∗cos60°
U o u t s i n ( θ − 60 ° ) = 2 3 U d c ∗ T x T s ∗ s i n 60 ° U_{out}sin(θ-60°) = \frac23U_{dc}*\frac {T_x} {T_s} * sin60° Uoutsin(θ−60°)=32Udc∗TsTx∗sin60°
可以看出Uα有涉及了Tx与Ty,而Uβ只有Tx,因此我们先求解Uβ中的Tx再代入Uα从而把Ty也求解出来
【Q】这里为什么是 θ − 60 ° θ-60° θ−60°?
【A】因为第二扇区的范围是60-120°,我们计算第二扇区需要偏移60°,从而映射0-60°,从而对应 U α = U o u t c o s θ U_α = U_{out}cosθ Uα=Uoutcosθ 和 U β = U o u t s i n θ U_β = U_{out}sinθ Uβ=Uoutsinθ
1. 解析扇区Ⅱ的 T x T_x Tx
U o u t s i n ( θ − 60 ° ) = 2 3 U d c ∗ T x T s ∗ s i n 60 ° U_{out}sin(θ-60°) = \frac23U_{dc}*\frac {T_x} {T_s} * sin60° Uoutsin(θ−60°)=32Udc∗TsTx∗sin60°
U o u t s i n ( θ − 60 ° ) = 2 3 U d c ∗ T x T s ∗ 3 2 U_{out}sin(θ-60°) = \frac23U_{dc}*\frac {T_x} {T_s} * \frac {\sqrt3}2 Uoutsin(θ−60°)=32Udc∗TsTx∗23
U o u t s i n ( θ − 60 ° ) = 1 3 U d c ∗ T x T s U_{out}sin(θ-60°) = \frac 1 {\sqrt3}U_{dc}*\frac {T_x}{T_s} Uoutsin(θ−60°)=31Udc∗TsTx
U o u t s i n ( θ − 60 ° ) = 1 3 U d c ∗ T x T s U_{out}sin(θ-60°) = \frac 1 {\sqrt3}U_{dc}*\frac {T_x}{T_s} Uoutsin(θ−60°)=31Udc∗TsTx
T x = 3 T s U d c U o u t s i n ( θ − 60 ° ) T_x= \frac {\sqrt3T_s}{U_{dc}}U_{out}sin(θ-60°) Tx=Udc3TsUoutsin(θ−60°)
T x = 3 T s U d c U o u t ( s i n θ c o s 60 ° − c o s θ s i n 60 ° ) T_x= \frac {\sqrt3T_s}{U_{dc}}U_{out}(sinθcos60°-cosθsin60°) Tx=Udc3TsUout(sinθcos60°−cosθsin60°)
T x = 3 T s U d c U o u t ( 1 2 s i n θ − 3 2 c o s θ ) T_x= \frac {\sqrt3T_s}{U_{dc}}U_{out}(\frac12sinθ-\frac{\sqrt3}2cosθ) Tx=Udc3TsUout(21sinθ−23cosθ)
T x = 3 T s U d c ( − 3 2 U α + 1 2 U β ) T_x=\frac {\sqrt3 T_s}{U_{dc}}( -\frac {\sqrt3}2U_α+\frac 1 2U_β ) Tx=Udc3Ts(−23Uα+21Uβ)
2. 解析扇区Ⅱ的 T y T_y Ty
U o u t c o s ( θ − 60 ° ) = 2 3 U d c ∗ T y T s + 2 3 U d c ∗ T x T s ∗ c o s 60 ° U_{out}cos(θ-60°) = \frac23U_{dc}*\frac {T_y} {T_s}+\frac23U_{dc}*\frac {T_x} {T_s}*cos60° Uoutcos(θ−60°)=32Udc∗TsTy+32Udc∗TsTx∗cos60°
U o u t c o s ( θ − 60 ° ) = 2 3 U d c ∗ T y T s + 2 3 U d c ∗ T x T s ∗ 1 2 U_{out}cos(θ-60°) = \frac23U_{dc}*\frac {T_y} {T_s}+\frac23U_{dc}*\frac {T_x} {T_s}*\frac12 Uoutcos(θ−60°)=32Udc∗TsTy+32Udc∗TsTx∗21
U o u t c o s ( θ − 60 ° ) = 2 3 U d c ∗ T y T s + 1 3 U d c ∗ T x T s U_{out}cos(θ-60°) = \frac23U_{dc}*\frac {T_y} {T_s}+\frac13U_{dc}*\frac {T_x} {T_s} Uoutcos(θ−60°)=32Udc∗TsTy+31Udc∗TsTx
U o u t c o s ( θ − 60 ° ) = 2 3 U d c ∗ T y T s + 1 3 U d c ∗ 3 T s U d c ( − 3 2 U α + 1 2 U β ) T s U_{out}cos(θ-60°) = \frac23U_{dc}*\frac {T_y} {T_s}+\frac13U_{dc}*\frac {\frac {\sqrt3 T_s}{U_{dc}}( -\frac {\sqrt3}2U_α+\frac 1 2U_β )} {T_s} Uoutcos(θ−60°)=32Udc∗TsTy+31Udc∗TsUdc3Ts(−23Uα+21Uβ)
U o u t c o s ( θ − 60 ° ) = 2 3 U d c ∗ T y T s − 3 3 ( − 3 2 U α + 1 2 U β ) U_{out}cos(θ-60°) = \frac23U_{dc}*\frac {T_y} {T_s} - \frac{ \sqrt3 }3( -\frac {\sqrt3}2U_α+\frac 1 2U_β ) Uoutcos(θ−60°)=32Udc∗TsTy−33(−23Uα+21Uβ)
T y = U o u t ( c o s θ c o s 60 ° + s i n θ s i n 60 ° ) − 3 3 ( − 3 2 U α + 1 2 U β ) 2 3 U d c T s T_y = \frac {U_{out}(cosθcos60°+sinθsin60°) - \frac{ \sqrt3 }3( -\frac {\sqrt3}2U_α+\frac 1 2U_β ) } {\frac 23U_{dc}}T_s Ty=32UdcUout(cosθcos60°+sinθsin60°)−33(−23Uα+21Uβ)Ts
T y = U α 1 2 + U β 3 2 + 1 2 U α − 3 6 U β 2 3 U d c T s T_y = \frac {Uα\frac12+Uβ\frac{\sqrt3}{2} + \frac 12U_α-\frac {\sqrt3} 6U_β } {\frac 23U_{dc}}T_s Ty=32UdcUα21+Uβ23+21Uα−63UβTs
T y = U α + U β 2 3 6 2 3 U d c T s T_y = \frac {Uα+Uβ\frac{2\sqrt3}{6} } {\frac 23U_{dc}}T_s Ty=32UdcUα+Uβ623Ts
T y = 3 U α + 3 U β 2 U d c T s T_y = \frac {3Uα+{\sqrt3}Uβ } {2U_{dc}}T_s Ty=2Udc3Uα+3UβTs
T x = 3 T s U d c ( 3 2 U α + 1 2 U β ) T_x=\frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α+\frac 1 2U_β ) Tx=Udc3Ts(23Uα+21Uβ)
2.3 扇区Ⅲ计算
根据上图解析出以下公式 :
U o u t c o s ( θ − 120 ° ) = 2 3 U d c ∗ T x T s + 2 3 U d c ∗ T y T s ∗ c o s 60 ° U_{out}cos(θ-120°) = \frac23U_{dc}*\frac {T_x} {T_s}+\frac23U_{dc}*\frac {T_y} {T_s}*cos60° Uoutcos(θ−120°)=32Udc∗TsTx+32Udc∗TsTy∗cos60°
U o u t s i n ( θ − 120 ° ) = 2 3 U d c ∗ T y T s ∗ s i n 60 ° U_{out}sin(θ-120°) = \frac23U_{dc}*\frac {T_y} {T_s} * sin60° Uoutsin(θ−120°)=32Udc∗TsTy∗sin60°
可以看出Uα有涉及了Tx与Ty,而Uβ只有Ty,因此我们先求解Uβ中的Ty再代入Uα从而把Tx也求解出来
【Q】这里为什么是 θ − 120 ° θ-120° θ−120°?
【A】因为第二扇区的范围是120-180°,我们计算第二扇区需要偏移120°,从而映射0-60°,从而对应 U α = U o u t c o s θ U_α = U_{out}cosθ Uα=Uoutcosθ 和 U β = U o u t s i n θ U_β = U_{out}sinθ Uβ=Uoutsinθ
1. 解析扇区Ⅲ的 T y T_y Ty
U o u t s i n ( θ − 120 ° ) = 2 3 U d c ∗ T y T s ∗ s i n 60 ° U_{out}sin(θ-120°) = \frac23U_{dc}*\frac {T_y} {T_s} * sin60° Uoutsin(θ−120°)=32Udc∗TsTy∗sin60°
U o u t s i n ( θ − 120 ° ) = 2 3 U d c ∗ T y T s ∗ 3 2 U_{out}sin(θ-120°) = \frac23U_{dc}*\frac {T_y} {T_s} * \frac {\sqrt3}2 Uoutsin(θ−120°)=32Udc∗TsTy∗23
U o u t s i n ( θ − 120 ° ) = 1 3 U d c ∗ T y T s U_{out}sin(θ-120°) = \frac 1 {\sqrt3}U_{dc}*\frac {T_y}{T_s} Uoutsin(θ−120°)=31Udc∗TsTy
U o u t s i n ( θ − 120 ° ) = 1 3 U d c ∗ T y T s U_{out}sin(θ-120°) = \frac 1 {\sqrt3}U_{dc}*\frac {T_y}{T_s} Uoutsin(θ−120°)=31Udc∗TsTy
T y = 3 T s U d c U o u t s i n ( θ − 120 ° ) T_y= \frac {\sqrt3T_s}{U_{dc}}U_{out}sin(θ-120°) Ty=Udc3TsUoutsin(θ−120°)
T y = 3 T s U d c U o u t ( s i n θ c o s 120 ° − c o s θ s i n 120 ° ) T_y= \frac {\sqrt3T_s}{U_{dc}}U_{out}(sinθcos120°-cosθsin120°) Ty=Udc3TsUout(sinθcos120°−cosθsin120°)
T y = 3 T s U d c U o u t ( − 1 2 s i n θ − 3 2 c o s θ ) T_y= \frac {\sqrt3T_s}{U_{dc}}U_{out}(-\frac12sinθ-\frac{\sqrt3}2cosθ) Ty=Udc3TsUout(−21sinθ−23cosθ)
T y = − 3 T s U d c ( 3 2 U α + 1 2 U β ) T_y=-\frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α+\frac 1 2U_β ) Ty=−Udc3Ts(23Uα+21Uβ)
2. 解析扇区Ⅲ的 T x T_x Tx
U o u t c o s ( θ − 120 ° ) = 2 3 U d c ∗ T x T s + 2 3 U d c ∗ T y T s ∗ c o s 60 ° U_{out}cos(θ-120°) = \frac23U_{dc}*\frac {T_x} {T_s}+\frac23U_{dc}*\frac {T_y} {T_s}*cos60° Uoutcos(θ−120°)=32Udc∗TsTx+32Udc∗TsTy∗cos60°
U o u t c o s ( θ − 120 ° ) = 2 3 U d c ∗ T x T s + 2 3 U d c ∗ T y T s ∗ 1 2 U_{out}cos(θ-120°) = \frac23U_{dc}*\frac {T_x} {T_s}+\frac23U_{dc}*\frac {T_y} {T_s}*\frac12 Uoutcos(θ−120°)=32Udc∗TsTx+32Udc∗TsTy∗21
U o u t c o s ( θ − 120 ° ) = 2 3 U d c ∗ T x T s + 1 3 U d c ∗ T y T s U_{out}cos(θ-120°) = \frac23U_{dc}*\frac {T_x} {T_s}+\frac13U_{dc}*\frac {T_y} {T_s} Uoutcos(θ−120°)=32Udc∗TsTx+31Udc∗TsTy
U o u t c o s ( θ − 120 ° ) = 2 3 U d c ∗ T x T s + 1 3 U d c ∗ − 3 T s U d c ( 3 2 U α + 1 2 U β ) T s U_{out}cos(θ-120°) = \frac23U_{dc}*\frac {Tx} {T_s}+\frac13U_{dc}*\frac {-\frac {\sqrt3 T_s}{U_{dc}}( \frac {\sqrt3}2U_α+\frac 1 2U_β )} {T_s} Uoutcos(θ−120°)=32Udc∗TsTx+31Udc∗Ts−Udc3Ts(23Uα+21Uβ)
U o u t c o s ( θ − 120 ° ) = 2 3 U d c ∗ T x T s − 3 3 ( 3 2 U α + 1 2 U β ) U_{out}cos(θ-120°) = \frac23U_{dc}*\frac {T_x} {T_s} - \frac{ \sqrt3 }3( \frac {\sqrt3}2U_α+\frac 1 2U_β ) Uoutcos(θ−120°)=32Udc∗TsTx−33(23Uα+21Uβ)
T x = U o u t ( c o s θ c o s 120 ° + s i n θ s i n 120 ° ) + 3 3 ( 3 2 U α + 1 2 U β ) 2 3 U d c T s T_x = \frac {U_{out}(cosθcos120°+sinθsin120°) + \frac{ \sqrt3 }3( \frac {\sqrt3}2U_α+\frac 1 2U_β ) } {\frac 23U_{dc}}T_s Tx=32UdcUout(cosθcos120°+sinθsin120°)+33(23Uα+21Uβ)Ts
T x = − 1 2 U α + 3 2 U β + 1 2 U α + 3 6 U β 2 3 U d c T s T_x = \frac {-\frac12Uα+\frac{\sqrt3}{2}Uβ + \frac 12U_α+\frac {\sqrt3} 6U_β } {\frac 23U_{dc}}T_s Tx=32Udc−21Uα+23Uβ+21Uα+63UβTs
T x = U β 2 3 3 2 3 U d c T s T_x = \frac {Uβ\frac{2\sqrt3}{3} } {\frac 23U_{dc}}T_s Tx=32UdcUβ323Ts
T x = 3 T s U d c U β T_x = \frac {\sqrt3 T_s}{U_{dc}}Uβ Tx=Udc3TsUβ
由于手敲公式占了太多字数空间,超出编辑字数,因此扇区计算分为两篇,扇区4,5,6计算可通过下方链接进入
[嵌入式专栏](FOC - SVPWM扇区计算Part2)
3 . 小结
计算出了SVPWM每个扇区的Tx与Ty就可以进行扇区输出了,下一篇讲解扇区输出调整,谢谢观看。
技术交流QQ群 : 745662457
群内专注 - 问题答疑,技术研究
图片资源本人在网上下载,若有侵权行为,请告知,本人会立刻删除
相关文章:

[嵌入式专栏](FOC - SVPWM扇区计算Part1)
文章目录 1 . 概要2 . 扇区计算2.1 扇区Ⅰ计算2.2 扇区Ⅱ计算2.3 扇区Ⅲ计算 3 . 小结 【极客技术传送门】 : https://blog.csdn.net/Engineer_LU/article/details/135149485 1 . 概要 经过扇区判断后,就知道在哪个扇区进行输出了 【Q】但是每个扇区分别输出怎样的结…...

亚马逊美国站ASTM F2613儿童折叠椅和凳子强制性安全标准
ASTM F2613折叠椅和凳子安全标准 美国消费品安全委员会(CPSC)发布的ASTM F2613儿童折叠椅和凳子的强制性安全标准,已于2020年7月6日生效,并被纳入联邦法规《16 CFR 1232儿童折叠椅和凳子安全标准》。 亚马逊要求在美国站上架的儿…...
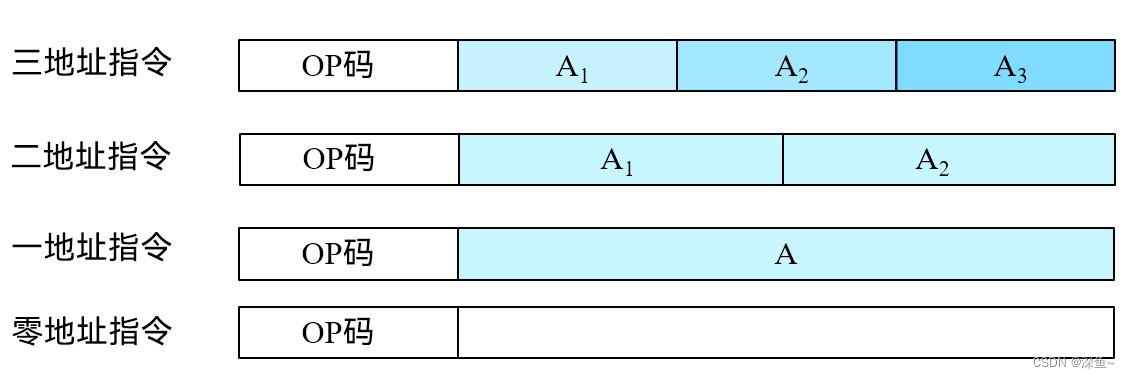
【机组期末速成】指令系统|机器指令概述|操作数类型与操作类型|寻址方式|指令格式
🎥 个人主页:深鱼~🔥收录专栏:计算机组成原理🌄欢迎 👍点赞✍评论⭐收藏 目录 前言: 一、本章考点总览 二、考点分析 1、以下有关指令系统的说法中错误的是( )。 2…...
java美容管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java Web美容管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…...

Redis哨兵
1.哨兵介绍 1.1.为何需要哨兵? 为了解决master节点宕机问题,选举salve节点为新的master节点。 1.2.哨兵的作用 1.3.服务状态监控 1.4.选举新的master 1.5.如何实现故障转移 2.搭建哨兵集群 2.1.集群结构 这里我们搭建一个三节点形成的Sentinel集群&…...
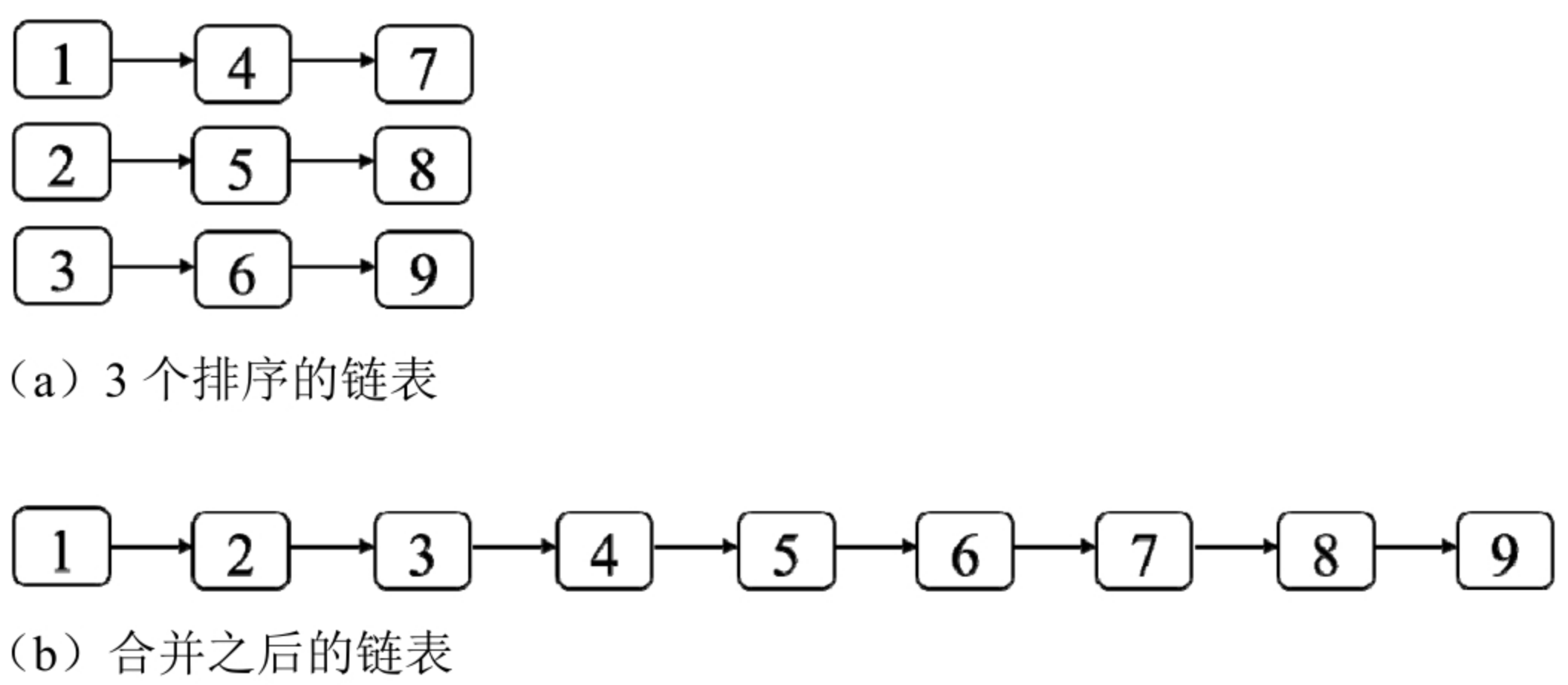
面试算法78:合并排序链表
题目 输入k个排序的链表,请将它们合并成一个排序的链表。 分析:利用最小堆选取值最小的节点 用k个指针分别指向这k个链表的头节点,每次从这k个节点中选取值最小的节点。然后将指向值最小的节点的指针向后移动一步,再比较k个指…...
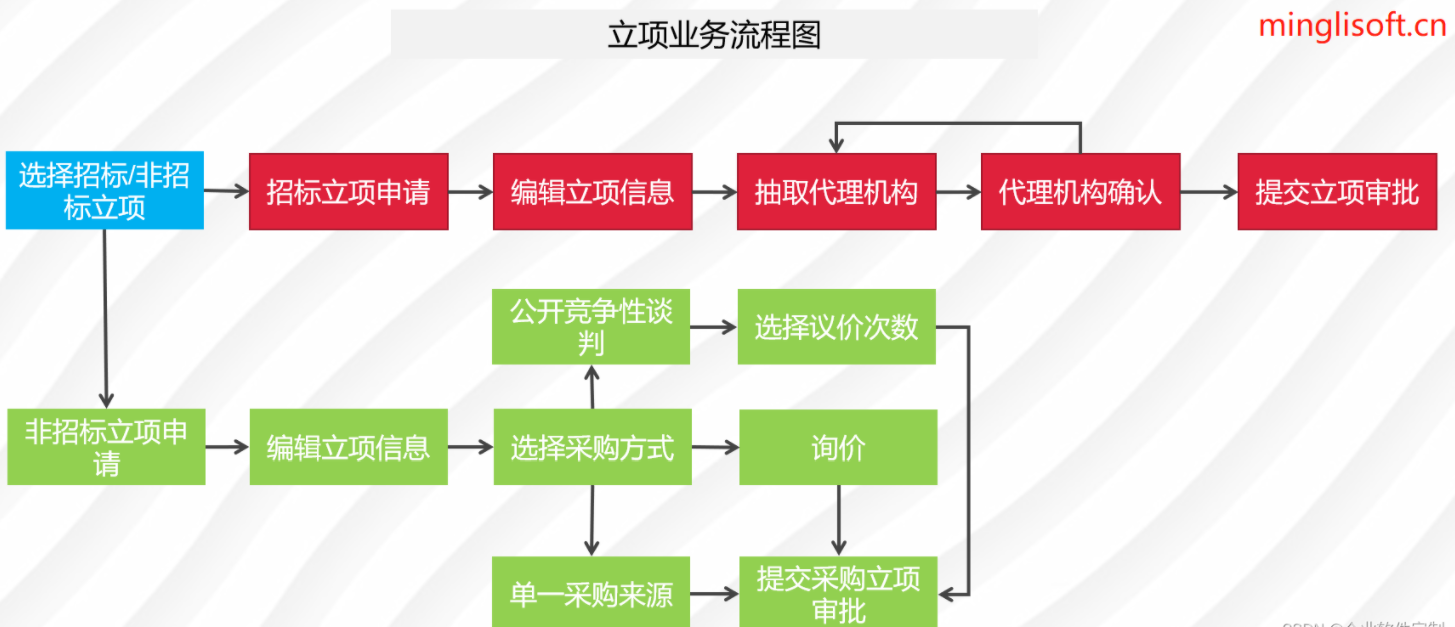
鸿鹄电子招投标系统:基于Spring Boot、Mybatis、Redis和Layui的企业电子招采平台源码与立项流程
在数字化时代,企业需要借助先进的数字化技术来提高工程管理效率和质量。招投标管理系统作为企业内部业务项目管理的重要应用平台,涵盖了门户管理、立项管理、采购项目管理、采购公告管理、考核管理、报表管理、评审管理、企业管理、采购管理和系统管理等…...

node.js对应npm安装和使用
介绍 node.js是一个基于 Chrome V8 引擎的 JavaScript 运行环境,安装node后自带npm。NPM :Node Package ManagerNPM是Node.js标准的软件包管理器 。2010年底,Node.js 的包管理器 npm 诞生,是全球最大的开源库生态系统。 node 20…...
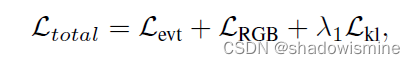
(self-supervised learning)Event Camera Data Pre-training
Publisher: ICCV 2023 MOTIVATION OF READING: 自监督学习、稀疏事件 NILM link: https://arxiv.org/pdf/2301.01928.pdf Code: GitHub - Yan98/Event-Camera-Data-Pre-training 1. Overview Contributions are summarized as follows: 1. A self-supervised framework f…...
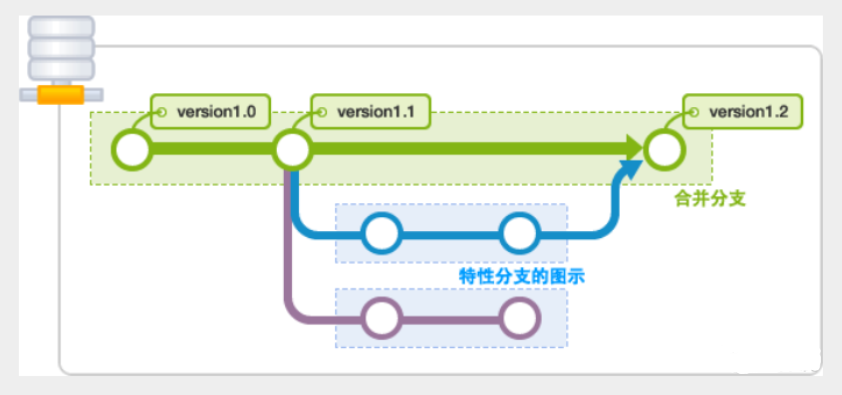
关于个人Git学习记录及相关
前言 可以看一下猴子都能懂的git入门,图文并茂不枯燥 猴子都能懂的git入门 学习东西还是建议尽可能的去看官方文档 权威且详细 官方文档 强烈建议看一下GitHub漫游指南及开源指北,可以对开源深入了解一下,打开新世界的大门! …...
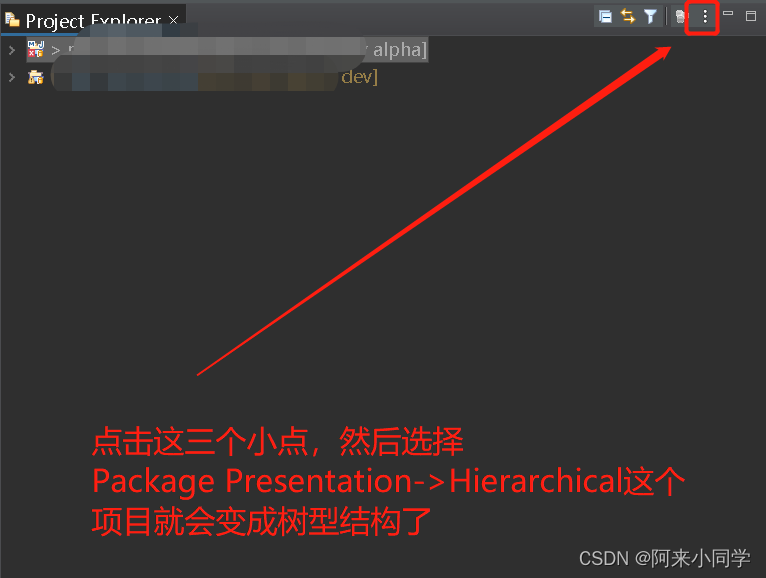
【eclipse】eclipse开发springboot项目使用入门
下载eclipse Eclipse downloads - Select a mirror | The Eclipse Foundation 安装eclipse 其他一步一步即可 我们是开发java web选择如下 界面修改 Window->Preferences-> 修改eclipse风格主题 Window->Preferences->General->Appearance 修改字体和大小…...

Android 13 默认关闭 快速打开相机
介绍 在设置菜单的手势界面里,快速打开相机是默认开启的,此功能当开启时连续点击两次电源键会打开相机,现在客户需要默认关闭。 效果展示 修改 这里一开始想到的就是配置文件,在路径下果然找到了,从注释中看使我们需要的&#x…...

pytest pytest-html优化样式
conftest.py import pytest from pytest_metadata.plugin import metadata_keydef pytest_html_report_title(report):report.title"接口测试报告"def pytest_configure(config):# 获取命令行参数中的测试环境、测试版本、开始时间、测试人员config.stash[metadata_…...

Visual Studio 配置DLL
我们在用Visual Studio进行开发时,如果没有正确配置DLL,就会出现类似“丢失***.dll”的错误。DLL配置有哪些方法? 1、手动复制 将dll文件拷贝到生成的.exe所在的文件夹里 2、配置环境 在右键属性->配置属性->调试->环境…...

C/C++转WebAssembly及微信小程序调用
上一篇文章讲了C/C如何转WebAssembly,并测试了在Web端调用。本篇内容和上篇一样,介绍C/C包转的.wasm包如何在小程序中调用。 说明 本篇是在上一篇步骤1-4的基础上,再做修改,供微信小程序端调用的方法和步骤。 本篇操作手册可以…...

【WPF.NET开发】弱事件模式
本文内容 先决条件为什么要实现弱事件模式?应该由谁实现弱事件模式?如何实现弱事件模式 在应用程序中,附加到事件源的处理程序可能不会与将处理程序附加到源的侦听器对象一同销毁。 这种情况下会导致内存泄漏。 Windows Presentation Found…...

[Angular] 笔记 16:模板驱动表单 - 选择框与选项
油管视频: Select & Option (Template Driven Forms) Select & Option 在 pokemon.ts 中新增 interface: export interface Pokemon {id: number;name: string;type: string;isCool: boolean;isStylish: boolean;acceptTerms: boolean; }// new interface…...
Webpack基础使用
目录 一.什么是Webpack 二.为什么要使用Webpack 三.Webpack的使用 1.下载yarn包管理器 2.Webpack的安装 3.Webpack的简单使用 4.效果 四.Webpack打包流程 一.什么是Webpack Webpack是一个静态模块打包工具 二.为什么要使用Webpack 在开发中,我们常常会遇到…...
扭蛋机小程序搭建:打造互联网“流量池”
随着互联网科技的发展,扭蛋机小程序成为了市场发展的重要力量。 扭蛋机市从日本发展流行起来的,玩法就是根据设置的概率,让玩家体验扭蛋机的乐趣。扭蛋机中有隐藏款和稀有款,为了获得稀有款商品,玩家便会进行扭蛋&…...
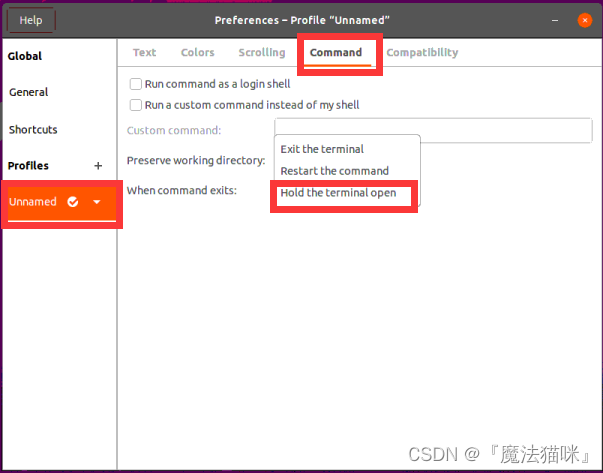
解决VNC连接Ubuntu服务器打开终端出现闪退情况
服务器环境 阿里云ECS服务器 操作系统:Ubuntu 20.0.4 如何使用VNC连接阿里云ECS服务器 1.阿里云官方指导:通过VNC搭建Ubuntu 18.04和20.04图形界面 2.新手入门ECS——ubuntu 20.04安装图形化界面和本地VNC连接 问题描述 使用VNC连接上新申请阿里云服…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
