【数学建模美赛M奖速成系列】Matplotlib绘图技巧(三)
Matplotlib绘图技巧(三)
- 写在前面
- 7. 雷达图
- 7.1 圆形雷达图
- 7.2 多边形雷达图
- 8. 极坐标图 subplot
- 9. 折线图 plot
- 10. 灰度图 meshgrid
- 11. 热力图
- 11.1 自定义colormap
- 12. 箱线图 boxplot
写在前面
终于更新完Matplotlib绘图技巧的全部内容,有需要完整文档的同学欢迎留言~
7. 雷达图
7.1 圆形雷达图
import matplotlib.pyplot as plt
import numpy as np
p1={"编程能力":60,"沟通技能":70,"专业知识":65,"团体协作":75,"工具掌握":80} #创建第一个人的数据
p2={"编程能力":70,"沟通技能":60,"专业知识":75,"团体协作":65,"工具掌握":70} #创建第二个人的数据
# 分别提取两个人的信息和对应的标签
data1=np.array([i for i in
p1.values()]).astype(int) #提取第一个人的信息
data2=np.array([i for i in
p2.values()]).astype(int) #提取第二个人的信息
label=np.array([j for j in p1.keys()]) #提取标签
angle = np.linspace(0, 2*np.pi, len(data1),
endpoint=False) #data里有几个数据,就把整圆360°分成几份
# 闭合的目的是在绘图时能够生成闭合的环
angles = np.concatenate((angle, [angle[0]])) #增加第一个angle到所有angle里,以实现闭合
data1 = np.concatenate((data1, [data1[0]])) #增加第一个人的第一个data到第一个人所有的data里,以实现闭合
data2 = np.concatenate((data2, [data2[0]])) #增加第二个人的第一个data到第二个人所有的data里,以实现闭合
fig = plt.figure()
ax = fig.add_subplot(111, polar=True) # 设置坐标轴为极坐标
# 绘制两个数据样本的闭合环
ax.plot(angles, data1, 'bo-', linewidth=2,
color='green', alpha=0.5)
ax.fill(angles, data1, facecolor='red',
alpha=0.2)
ax.plot(angles, data2, 'bo-', linewidth=2,
color='blue', alpha=0.5) #
ax.fill(angles, data2, facecolor='steelblue',
alpha=0.5)
# 设置圆周每一维上显示的样本
ax.set_thetagrids(angles * 180/np.pi, label,
fontproperties='SimHei', color='gray',
fontsize=13)
# 设置在半径方向上要显示的文本和显示文本的角度
ax.set_rgrids(np.arange(0, 81, 20),angle=45)
ax.set_rlim(0, 100)
ax.set_title('matplotlib 雷达图', va='bottom',
fontproperties='SimHei', color='gold',
fontsize=15)
#help(ax.set_thetagrids)
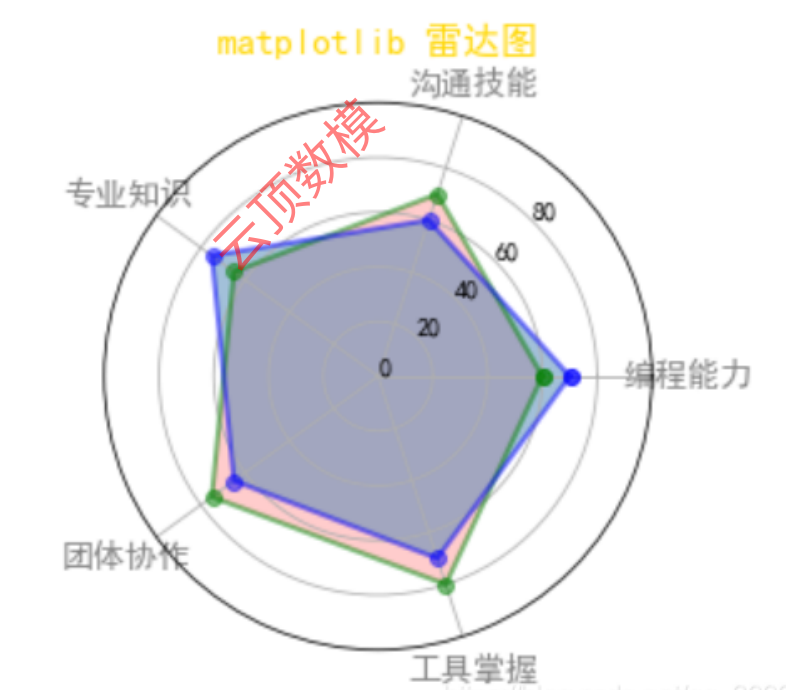
7.2 多边形雷达图
import numpy as np
import matplotlib.pyplot as plt
def plot_radar(data):
criterion = [1, 1, 1, 1, 1, 1] # 基准雷达图
angles = np.linspace(0, 2 * np.pi, 5,
endpoint=False)
angles = np.concatenate((angles, [angles[0]]))
#print(criterion)
#print(angles)
fig = plt.figure(facecolor='#87CEEB') # 创建画板
并填充颜色
ax = fig.add_subplot(111, polar=True,) # 设置
坐标为极坐标
# 绘制三个五边形
floor = 0
ceil = 2
labels = np.array(['x1', 'x2', 'x3', 'x4',
'x5'])
# 绘制五边形的循环
for i in np.arange(floor, ceil + 0.5 ,0.5):
ax.plot(angles, [i] * (6), '-', lw= 0.5,
color='black')
for i in range(5):
ax.plot([angles[i], angles[i]], [floor,
ceil], '-',lw=0.5, color='black')
# 绘制雷达图
ax.plot(angles, criterion, 'b-', lw=2,
alpha=0.4)
ax.fill(angles, criterion, facecolor='b',
alpha=0.3) #填充
ax.plot(angles, data, 'b-', lw=2, alpha=0.35)
ax.fill(angles, data, facecolor='b',
alpha=0.25)
ax.set_thetagrids(angles * 180 / np.pi,
labels)
ax.spines['polar'].set_visible(False)#不显示极坐最外的圆形
ax.set_theta_zero_location('N')#设置极坐标的起点(即0度)在正上方向
ax.grid(False)# 不显示分隔线
ax.set_yticks([]) # 不显示坐标间隔
ax.set_title('xxxxxxxxxxxx', va='bottom',
fontproperties='SimHei')
ax.set_facecolor('#87ceeb') # 填充绘图区域的颜色
# 保存文png图片
plt.subplots_adjust(left=0.09, right=1,
wspace=0.25, hspace=0.25, bottom=0.13, top=0.91)
plt.savefig('a_1.png')
plt.show()
data = [0.8, 0.9, 1.2, 1.0, 1.5, 0.8]
plot_radar(data)
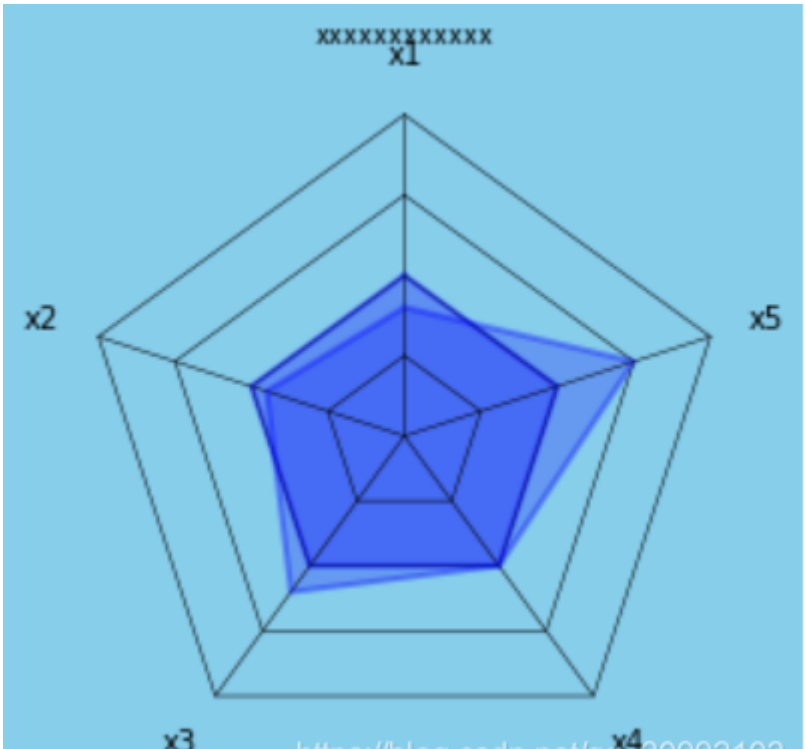
8. 极坐标图 subplot
import matplotlib.pyplot as plt
import numpy as np
N=20
theta=np.linspace(0,2*np.pi,N,endpoint=False)#均分角度
radii=10*np.random.rand(N)#随机角度
width=np.pi/4*np.random.rand(N)#随机宽度
ax=plt.subplot(111,projection='polar')#极坐标图绘制
bars=ax.bar(theta,radii,width=width,bottom=0.0)#哪个角度画,长度,扇形角度,从距离圆心0的地方开始画
for r,bar in zip(radii,bars):
bar.set_facecolor(plt.cm.viridis(r/10.0))
bar.set_alpha(0.5) #添加颜色
plt.title('polar')
plt.show()
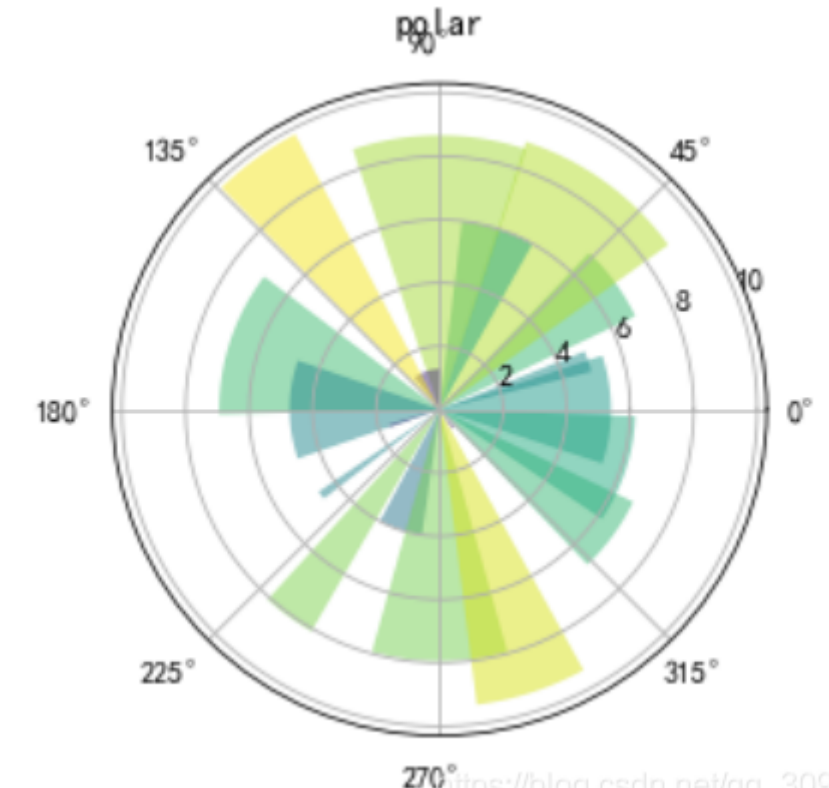
9. 折线图 plot
import matplotlib.pyplot as plt
x = [5, 10, 15, 20, 25, 30, 35, 40]
y = [17, 24, 29, 36, 38, 47, 59, 80]
plt.plot(x, y, 'rs-', markersize=10)
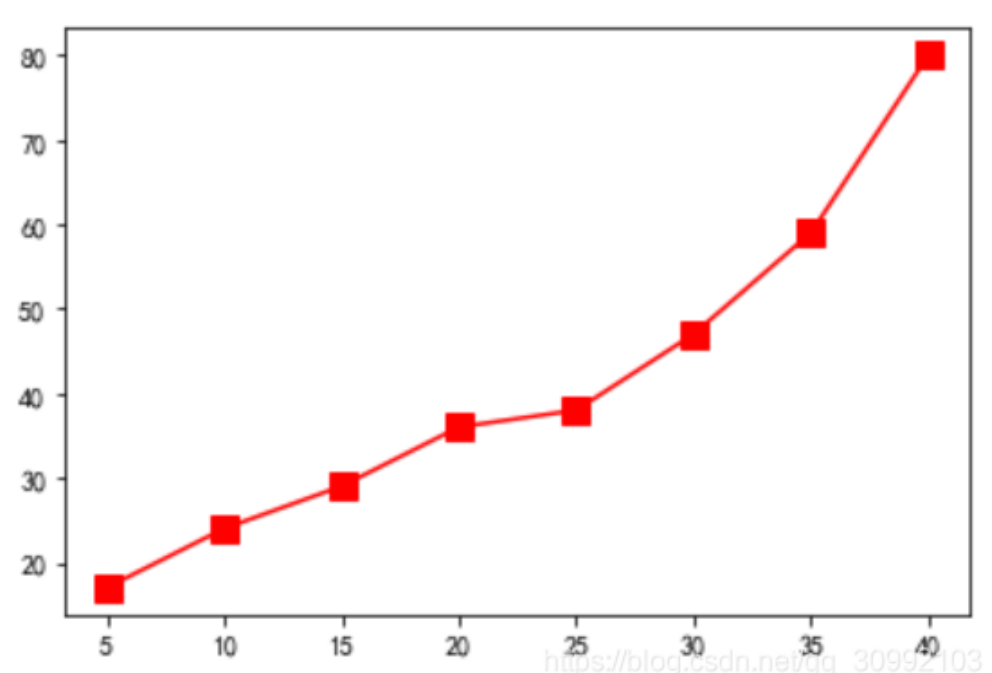
10. 灰度图 meshgrid
灰度图和热力图的区别其实在于colormap的不同,灰度图采用的灰度map,而热力图一般采用的是多个颜色组成的彩色的map。
import numpy as np
import matplotlib.pyplot as plt
def f(x,y):
return (1-x/2+x *5+y *3)*np.exp(-x *2-y *2)
n = 10
x = np.linspace(-3,3,3.5*n)
y = np.linspace(-3,3,3.0*n)
X,Y = np.meshgrid(x,y)
Z = f(X,Y)
plt.axes([0.025,0.025,0.95,0.95])
plt.imshow(Z, interpolation='bicubic',
cmap='bone', origin='lower')
plt.colorbar(shrink=0.9
plt.xticks([]), plt.yticks([])
# savefig(' ./figures/imshow_ex.png', dpi=48)
plt.show()

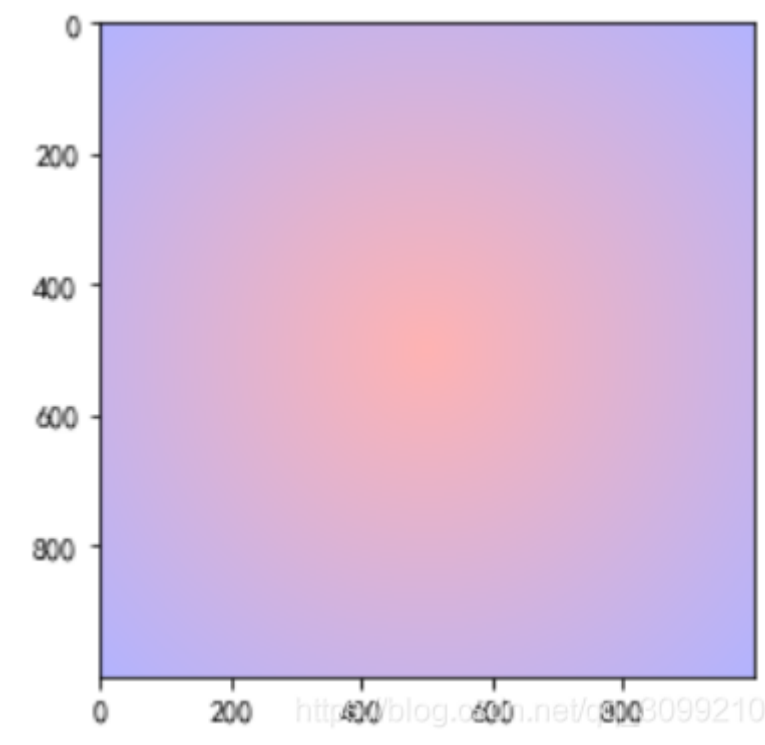
11. 热力图
import matplotlib.pyplot as plt
import matplotlib.colors as col
import matplotlib.cm as cm
import numpy as np
points = np.arange(-5, 5, 0.01)
# print(points)
xs, ys = np.meshgrid(points, points)
z = np.sqrt(xs *2 + ys *2)
# print(z)
# 自定义colormap
start_color = 'red'
end_color = 'blue'
cmap_1 =
col.LinearSegmentedColormap.from_list('cmap1',
[start_color, end_color])
plt.imshow(z, cmap=cmap_1, alpha=0.3)
plt.show()
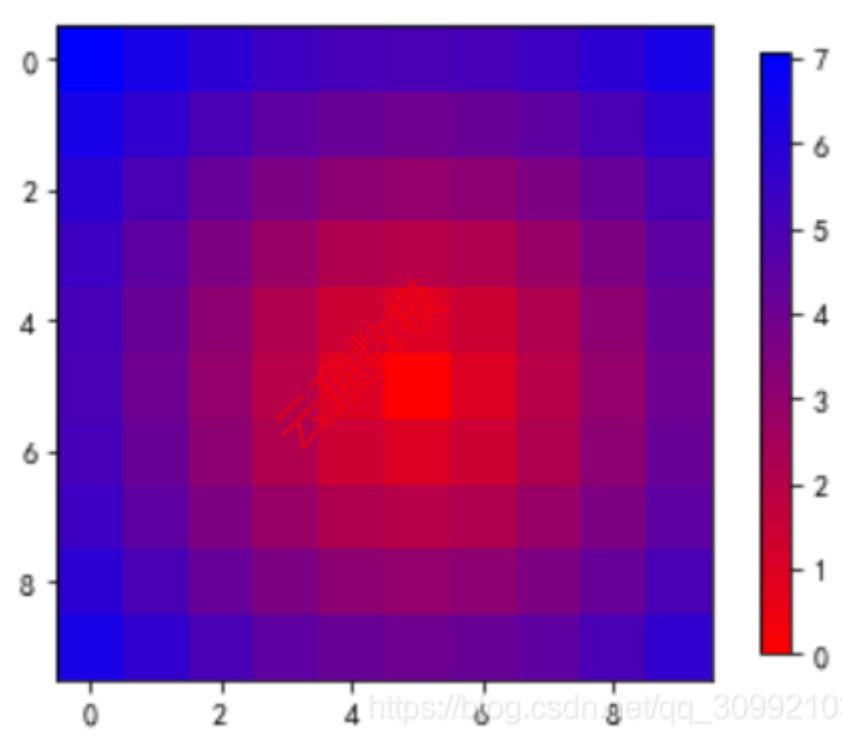
11.1 自定义colormap
import matplotlib.pyplot as plt
points = np.arange(-5, 5, 1)
# print(points)
xs, ys = np.meshgrid(points, points)
z = np.sqrt(xs *2 + ys *2)
# 列表中包含的颜色数目并不固定,可以选多个
color = ['red', 'green', 'blue']
cmap_1 =
col.LinearSegmentedColormap.from_list('cmap1',
[start_color, end_color])
plt.imshow(z, cmap=cmap_1, alpha=1)
plt.colorbar(shrink=0.92)
plt.show()
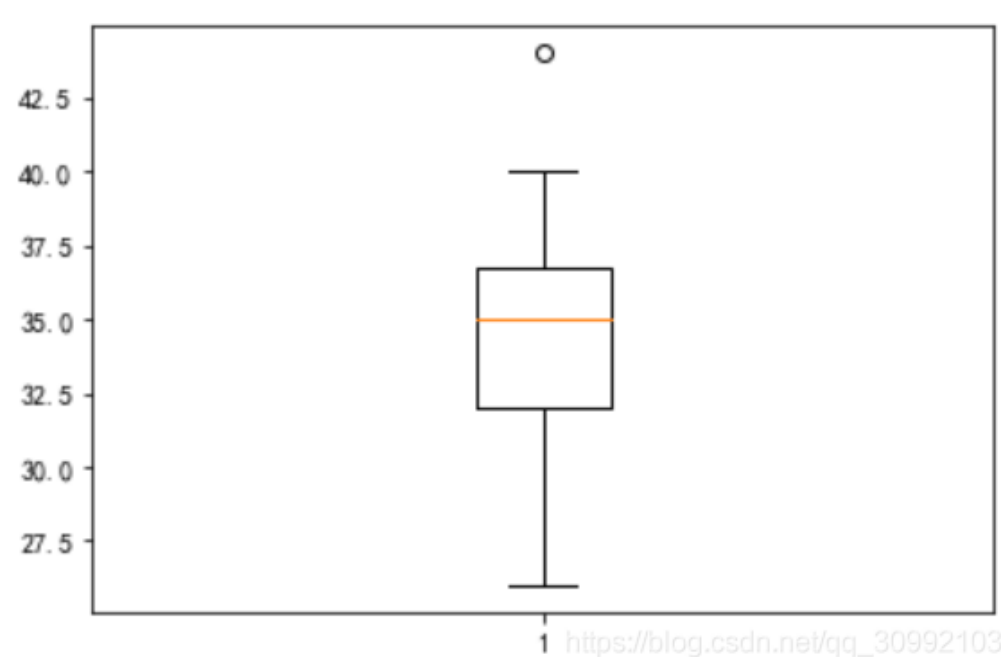
12. 箱线图 boxplot
箱线图是一种用作显示一组数据分散情况的统计图
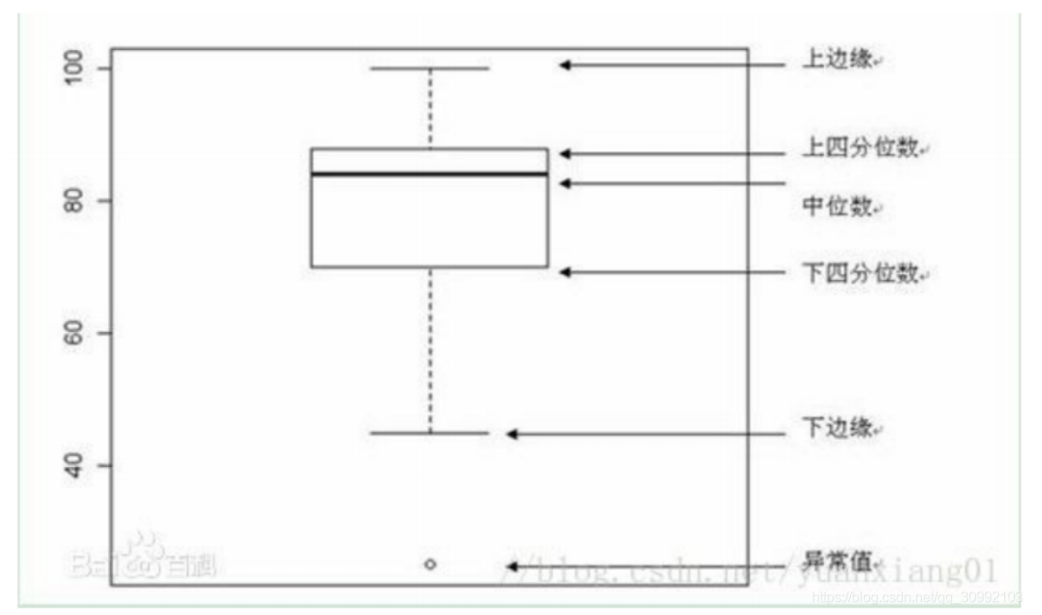
箱线图有五个参数,分别为:
- 下边缘(Q1),表示最小值;
- 下四分位数(Q2),又称“第一四分位数”,等于该样本中所有数值由小到大排列后第25%的数字;
- 中位数(Q3),又称“第二四分位数”等于该样本中所有数值由小到大排列后第50%的数字;
- 上四分位数(Q4),又称“第三四分位数”等于该样本中所有
- 数值由小到大排列后第75%的数字;
- 上边缘(Q5),表述最大值。
箱线图各参数和正态分布之间的对比如下图:
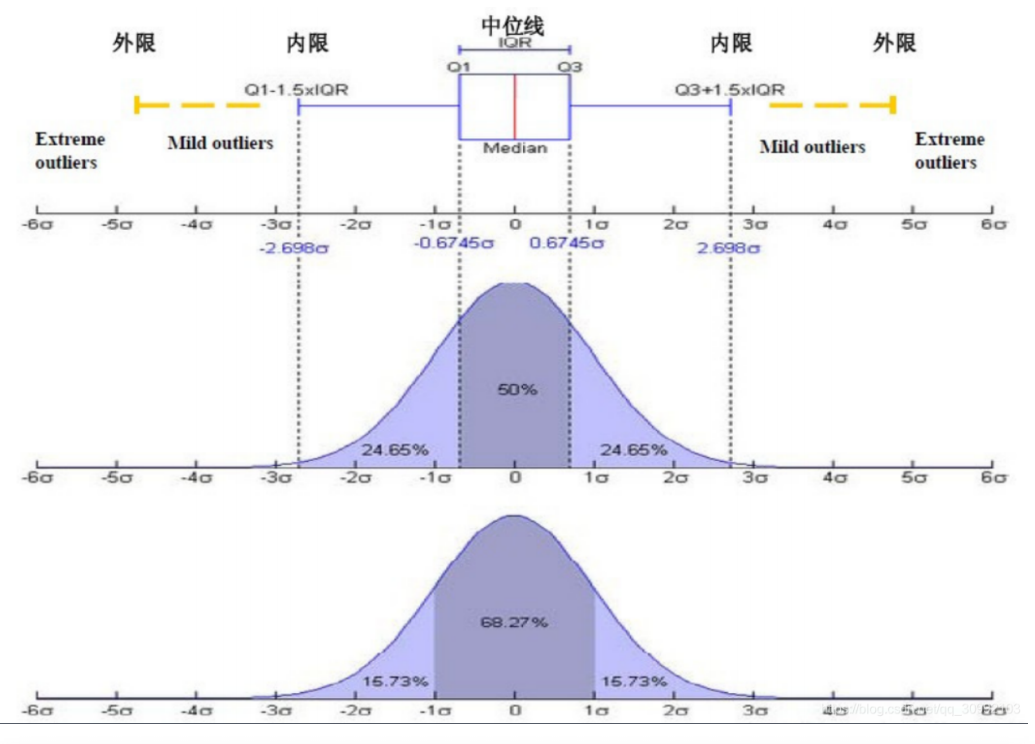
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import numpy as np
# 0、导入数据集
df = pd.read_excel('boxplot_data.xlsx', 'Sheet1')
fig = plt.figure()
ax = fig.add_subplot(111)
ax.boxplot(df['Age'])
plt.show()
相关文章:

【数学建模美赛M奖速成系列】Matplotlib绘图技巧(三)
Matplotlib绘图技巧(三) 写在前面7. 雷达图7.1 圆形雷达图7.2 多边形雷达图 8. 极坐标图 subplot9. 折线图 plot10. 灰度图 meshgrid11. 热力图11.1 自定义colormap 12. 箱线图 boxplot 写在前面 终于更新完Matplotlib绘图技巧的全部内容,有…...

手写Spring与基本原理--简易版
文章目录 手写Spring与基本原理解析简介写一个简单的Bean加载容器定义一个抽象所有类的BeanDefinition定义一个工厂存储所有的类测试 实现Bean的注册定义和获取基于Cglib实现含构造函数的类实例化策略Bean对象注入属性和依赖Bean的功能Spring.xml解析和注册Bean对象实现应用上下…...
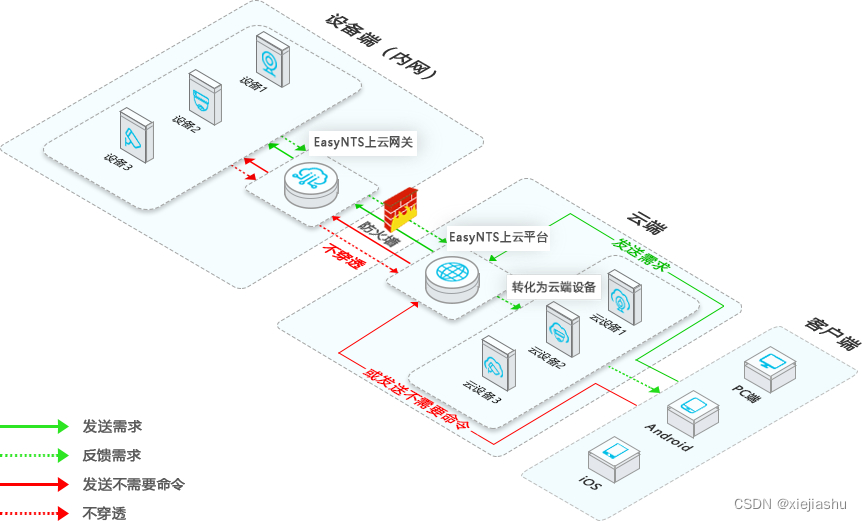
EasyNTS端口穿透服务新版本发布 0.8.7 增加隧道流量总数记录,可以知晓设备哪个端口耗费流量了
EasyNTS上云平台可通过远程访问内网应用,包含网络桥接、云端运维、视频直播等功能,极大地解决了现场无固定IP、端口不开放、系统权限不开放等问题。平台可提供一站式上云服务,提供直播上云、设备上云、业务上云、运维上云服务,承上…...

python自动合计各部周销
下载依赖 pip install openpyxl -i https://pypi.doubanio.com/simplepip install pandas -i https://pypi.doubanio.com/simple引入依赖 from openpyxl import load_workbook from openpyxl import styles from openpyxl.styles import * import pandas as pd import string…...

Java内存区域与内存溢出异常
Java与C++之间有一堵由内存分配和垃圾收集技术所围成的高墙,墙外面的人想进去,墙里面的人却想出来。 2.1 概述 对于从事C、C++程序开发的开发人员来说,在内存管理领域,他们即是拥有最高权力的“皇帝”,又是从事最基础工作的劳动人民——即拥有每一个对象的“所有权”,又…...
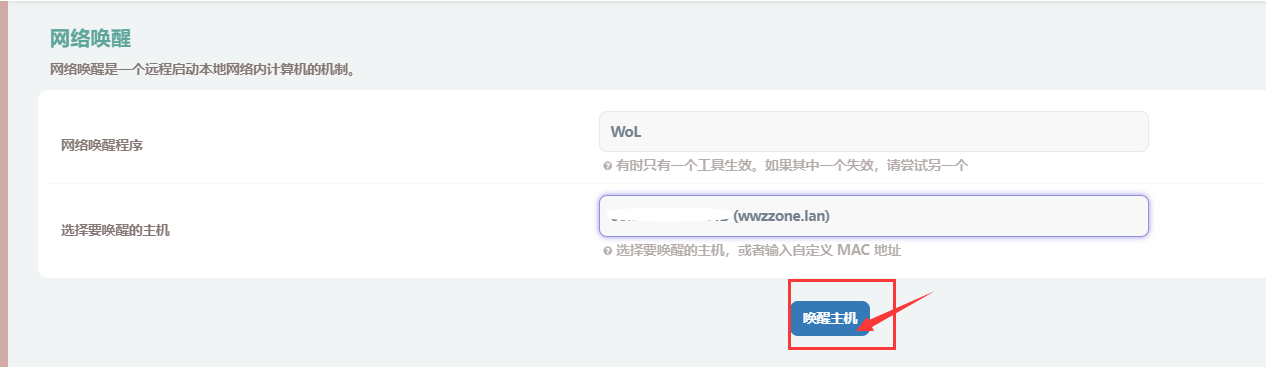
远程网络唤醒家庭主机(openwrt设置)
远程网络唤醒家庭主机(openwrt设置) 前提: 1.配置好主板bios的网络唤醒功能(网络教程自己百度一下找) 2.电脑开启网络唤醒功能(网络教程自己百度一下找) 3.路由器通过ddns实现域名和动态IP绑定内网穿透方法汇总_不修改光猫进行内网穿透-C…...
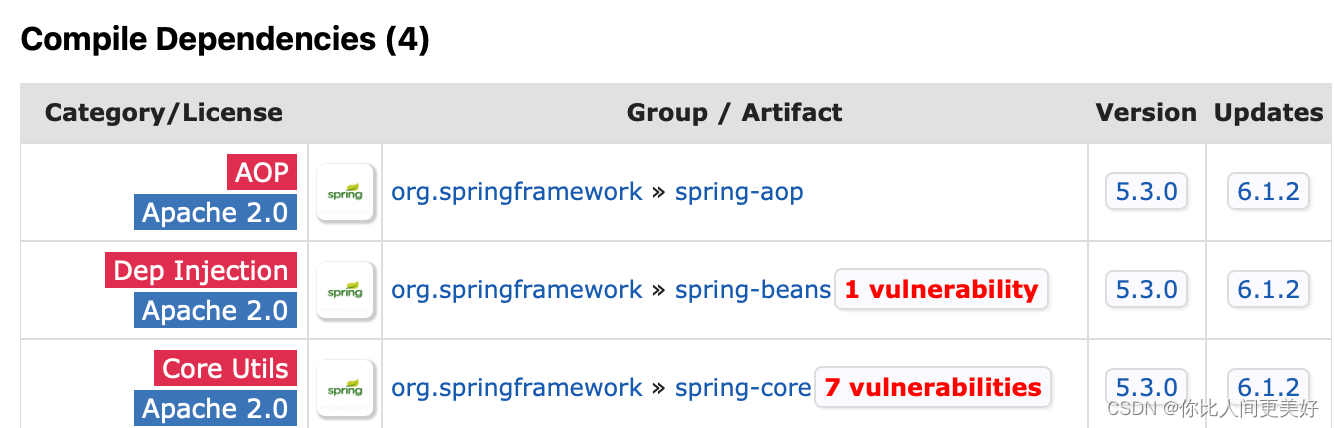
Spring知识02
1、这边是做单元测试的 2、项目部署上线的时候需要把Test那里注解掉 3、pom.xml的坐标系,用来导出包给别人用 4、项目名称,artifactId,name属性名保持一致 5、maven中央仓库那里可以看到导包之后会随着附加的内容 6、class.getSingleName获取…...

Linux服务器搭建笔记-006:拓展/home目录容量
一、问题说明 Ubuntu服务器在使用过程中创建的新用户,每位用户会在/home目录下生成一个属于其个人的主文件夹。如果不限制各个用户的使用空间,所有的用户都会共用/home所挂载的硬盘。在这种多用户情况下,会很快的填满/home目录,导…...

元宇宙与VR虚拟现实的未来如何?
从科幻小说到商业现实 自从 Facebook年更名为 Meta 以来,关于元宇宙的热议不断,人们对虚拟世界的兴趣也重新燃起,因为尽管虚拟现实 (VR) 的概念由来已久,但该技术现在才开始真正得以应用。 定义元宇宙和虚拟现实 首先是 The Met…...

微服务事务处理:CAP 定理和最终一致性的关系
CAP 定理和最终一致性 CAP 定理和最终一致性是两个密切相关的概念,但它们在范围和细节上有所不同。以下是比较: CAP 定理 **正式陈述:**在分布式系统中,最多只能同时满足以下三个保证中的两个:一致性、可用性和分区…...
【Linux操作系统】探秘Linux奥秘:操作系统的入门与实战
🌈个人主页:Sarapines Programmer🔥 系列专栏:《操作系统实验室》🔖诗赋清音:柳垂轻絮拂人衣,心随风舞梦飞。 山川湖海皆可涉,勇者征途逐星辉。 目录 🪐1 初识Linux OS …...

Copilot概述:AI助手引领编程新纪元
前言: 随着人工智能(AI)技术的不断进步,编程领域也在逐渐迎来一场革命。GitHub Copilot,作为一款由 OpenAI 和 GitHub 合作开发的编程助手,引发了广泛的关注和讨论。本篇博客将全面概述 Copilot 的背景、功…...

最小覆盖子串(LeetCode 76)
文章目录 1.问题描述2.难度等级3.热门指数4.解题思路参考文献 1.问题描述 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。 注意: 对于 t 中重复字符ÿ…...

Windows Sockets 2 笔记
文章目录 一、Winsock简介二、Windows中Winsock对网络协议支持的情况三、使用Winsock3.1 关于服务器和客户端3.2 创建基本Winsock应用程序3.3 初始化Winscok3.3.1 初始化步骤3.3.2 初始化的核心代码3.3.3 WSAStartup函数的协调3.3.4 WSACleanup函数3.3.5 初始化的完整代码 3.4 …...

13章总结
一.泛型 1.定义泛型类 泛型机制语法: 类名<T> 其中,T是泛型的名称,代表某一种类型。 【例13.6】创建带泛型的图书类 代码: 结果: 2.泛型的常规用法 (1)定义泛型类时声明多个变量 class MyClass<T1,T2>…...
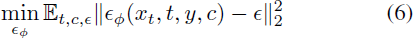
(2023,3D NeRF,无图像变分分数蒸馏,单步扩散)SwiftBrush:具有变分分数蒸馏的一步文本到图像扩散模型
SwiftBrush : One-Step Text-to-Image Diffusion Model with Variational Score Distillation 公众:EDPJ(添加 VX:CV_EDPJ 或直接进 Q 交流群:922230617 获取资料) 目录 0. 摘要 1. 方法 1.1 基础 1.2 SwiftBrus…...

【WPF.NET开发】将路由事件标记为已处理和类处理
本文内容 先决条件何时将路由事件标记为已处理预览和浮升路由事件对实例和类路由事件处理程序复合控件中的输入事件禁止 尽管对于何时将路由事件标记为已处理没有绝对规则,但如果代码以重要方式响应事件,请考虑将事件标记为已处理。 标记为已处理的路由…...

2023年03月18日_微软office365 copilot相关介绍
文章目录 Copilot In WordCopilot In PowerpointCopilot In ExcelCopilot In OutlookCopilot In TeamsBusiness Chat1 - copilot in word2 - copilot in excel3 - copilot in powerpoint4 - copilot in outlook5 - copilot in teams6 - business chat word 1、起草草稿 2、自动…...
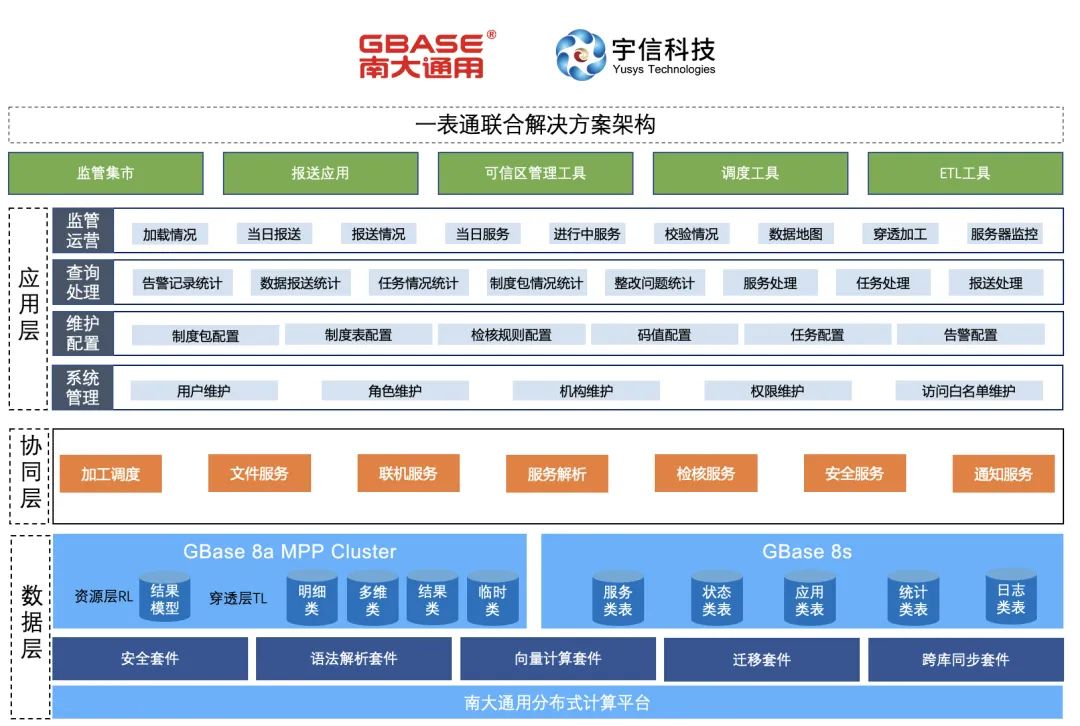
GBASE南大通用携手宇信科技打造“一表通”全链路解决方案
什么是“一表通”? “一表通”是国家金融监督管理总局为发挥统计监督效能、完善银行保险监管统计制度、推进监管数据标准化建设、打破数据壁垒,而制定的新型监管数据统计规范。相较于以往的报送接口,“一表通”提高了对报送时效性、校验准确…...

Python 内置高阶函数练习(Leetcode500.键盘行)
Python 内置高阶函数练习(Leetcode500.键盘行) 【一】试题 (1)地址: 500. 键盘行 - 力扣(LeetCode) (2)题目 给你一个字符串数组 words ,只返回可以使用在…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
