最优化方法Python计算:无约束优化应用——神经网络回归模型
人类大脑有数百亿个相互连接的神经元(如下图(a)所示),这些神经元通过树突从其他神经元接收信息,在细胞体内综合、并变换信息,通过轴突上的突触向其他神经元传递信息。我们在博文《最优化方法Python计算:无约束优化应用——逻辑回归模型》中讨论的逻辑回归模型(如下图(b)所示)与神经元十分相似,由输入端接收数据 x = ( x 1 x 2 ⋮ x n ) \boldsymbol{x}=\begin{pmatrix} x_1\\x_2\\\vdots\\x_n \end{pmatrix} x= x1x2⋮xn ,作加权和 ∑ i = 1 n w i x i \sum\limits_{i=1}^nw_ix_i i=1∑nwixi加上偏移量 b b b,即 ∑ i = 1 n w i x i + b \sum\limits_{i=1}^nw_ix_i+b i=1∑nwixi+b,用逻辑函数将其映射到区间 ( 0 , 1 ) (0,1) (0,1)内,然后将如此变换所得的信息 y y y输出。

这启发人们将诸多逻辑回归模型分层连接起来,构成人工神经网络,创建出多层感应模型。下图展示了一个包括输入层、输出层和两个隐藏层(图中阴影部分)的人工神经网络。图中,黑点表示数据节点,圆圈表示人工神经元的处理节点。

记逻辑函数 sigmoid ( x ) = 1 1 + e − x = φ ( x ) \text{sigmoid}(x)=\frac{1}{1+e^{-x}}=\varphi(x) sigmoid(x)=1+e−x1=φ(x)。设多层感应模型的输入数据为 n n n维向量 x = ( x 1 x 2 ⋮ x n ) \boldsymbol{x}=\begin{pmatrix} x_1\\x_2\\\vdots\\x_n \end{pmatrix} x= x1x2⋮xn 。不算输入层,模型连同输出层及隐藏层共有 l l l层。记 m 0 = n m_0=n m0=n,第 i i i层( 0 < i ≤ l 0<i\leq l 0<i≤l)含有 m i m_i mi个神经元。于是,相邻的两层,第 i − 1 i-1 i−1和第 i i i之间共有 ( m i − 1 + 1 ) m i (m_{i-1}+1)m_{i} (mi−1+1)mi个待定参数。因此,模型具有
p = ∑ i = 1 l ( m i − 1 + 1 ) m i p=\sum_{i=1}^l(m_{i-1}+1)m_i p=i=1∑l(mi−1+1)mi
个待定参数,组织成 p p p维向量 w = ( w 1 w 2 ⋮ w p ) \boldsymbol{w}=\begin{pmatrix} w_1\\w_2\\\vdots\\w_p \end{pmatrix} w= w1w2⋮wp 。设 k 0 = 0 k_0=0 k0=0,对 1 < i ≤ l 1<i\leq l 1<i≤l, k i = ∑ t = 0 i − 1 ( m t + 1 ) m t + 1 k_i=\sum\limits_{t=0}^{i-1}(m_{t}+1)m_{t+1} ki=t=0∑i−1(mt+1)mt+1,记 ( m i − 1 − 1 ) × m i (m_{i-1}-1)\times m_i (mi−1−1)×mi矩阵
w i = ( w k i + 1 ⋯ w k i + ( m i − 1 + 1 ) ( m i − 1 ) + 1 ⋮ ⋱ ⋮ w k i + ( m i − 1 + 1 ) ⋯ w k i + ( m i − 1 + 1 ) m i ) , i = 1 , 2 ⋯ , l \boldsymbol{w}_i=\begin{pmatrix} w_{k_i+1}&\cdots&w_{k_i+(m_{i-1}+1)(m_i-1)+1}\\ \vdots&\ddots&\vdots\\ w_{k_i+(m_{i-1}+1)}&\cdots&w_{k_i+(m_{i-1}+1)m_i} \end{pmatrix}, i=1,2\cdots,l wi= wki+1⋮wki+(mi−1+1)⋯⋱⋯wki+(mi−1+1)(mi−1)+1⋮wki+(mi−1+1)mi ,i=1,2⋯,l
定义函数
F ( w ; x ) = φ ( ( ⋯ φ ⏟ l ( ( x ⊤ , 1 ) w 1 ) , 1 ) , ⋯ ) , 1 ) w l ) . F(\boldsymbol{w};\boldsymbol{x})=\underbrace{\varphi((\cdots\varphi}_l((\boldsymbol{x}^\top,1)\boldsymbol{w}_1),1),\cdots),1)\boldsymbol{w}_l). F(w;x)=l φ((⋯φ((x⊤,1)w1),1),⋯),1)wl).
该函数反映了数据从输入层到输出层的传输方向,称为前向传播函数,作为多层感应模型的拟合函数。按此定义,我们构建如下的多层感应模型类
import numpy as np #导入numpy
class MLPModel(LogicModel): #多层感应模型def construct(self, X, hidden_layer_sizes): #确定网络结构if len(X.shape)==1: #计算输入端节点数k = 1else:k = X.shape[1]self.layer_sizes = (k,)+hidden_layer_sizes+(1,) def patternlen(self): #模式长度p = 0l = len(self.layer_sizes) #总层数for i in range(l-1): #逐层累加m = self.layer_sizes[i]n = self.layer_sizes[i+1]p += (m+1)*nreturn pdef F(self, w, x): #拟合函数l = len(self.layer_sizes) #总层数m, n = self.layer_sizes[0],self.layer_sizes[1]k = (m+1)*n #第0层参数个数W = w[0:k].reshape(m+1,n) #0层参数折叠为矩阵z = LogicModel.F(self, W, x) #第1层的输入for i in range(1, l-1): #逐层计算m = self.layer_sizes[i] #千层节点数n = self.layer_sizes[i+1] #后层节点数W = w[k:k+(m+1)*n].reshape(m+1,n) #本层参数矩阵z = np.hstack((z, np.ones(z.shape[0]). #本层输入矩阵reshape(z.shape[0], 1)))z = LogicModel.F(self, W, z) #下一层输入k += (m+1)*n #下一层参数下标起点y = z.flatten() #展平输出return ydef fit(self, X, Y, w = None, hidden_layer_sizes = (100,)): #重载训练函数self.construct(X, hidden_layer_sizes)LogicModel.fit(self, X, Y, w)
class MLPRegressor(Regression, MLPModel):'''神经网络回归模型'''
MLPModel继承了LogicModel类(详见博文《最优化方法Python计算:无约束优化应用——逻辑回归模型》)在MLPModel中除了重载模式长度计算函数patternlen、拟合函数F和训练函数fit外,增加了一个LogicModel类所没有的对象函数construct,用来确定神经网络的结构:有少层,各层有多少个神经元。
具体而言,第3~8行的construct函数,利用传递给它的输入矩阵X和隐藏层结构hidden_layer_sizes,这是一个元组,计算神经网络的各层结构。第4~7行的if-else分支按输入数据X的形状确定输入层的节点数k。第8行将元组(k,1)和(1,)分别添加在hidden_layer_sizes的首尾两端,即确定了网络结构layer_sizes。
第9~16行重载了模式长度计算函数patternlen。第11行根据模型的结构元组layer_sizes的长度确定层数l。第12~15行的for循环组成计算各层的参数个数:m为前层节点数(第13行),n为后层节点数(第14行),则第15行中(m+1)*n就是本层的参数个数,这是因为后层的每个节点的输入必须添加一个偏移量。第16行将算得的本层参数个数累加到总数p(第10行初始化为0)。
第17~32行重载拟合函数F,参数中w表示模式 w ∈ R p \boldsymbol{w}\in\text{R}^p w∈Rp,x表示自变量 ( x ⊤ , 1 ) (\boldsymbol{x}^\top,1) (x⊤,1)。第18行读取网络层数l。第19~22行计算第1隐藏层的输入:第19行读取第0层节点数m第1隐藏层节点数n。第20行计算第0层参数个数k(也是第1层参数下标起点)。第22行构造第0层的参数矩阵W。第22行计算 φ ( ( x ⊤ , 1 ) w 1 ) \varphi((\boldsymbol{x}^\top,1)\boldsymbol{w}_1) φ((x⊤,1)w1),作为第1隐藏层的输入z。第23~20行的for循环依次逐层构造本层参数矩阵 w i \boldsymbol{w}_i wi(第26行)和输入 ( z i ⊤ , 1 ) (\boldsymbol{z}_i^\top,1) (zi⊤,1)(第27~28行),第30行计算下一层的输入 φ ( ( z i ⊤ , 1 ) w i ) \varphi((\boldsymbol{z}_i^\top,1)\boldsymbol{w}_i) φ((zi⊤,1)wi)为z,第30行更新下一层参数下标起点k。完成循环,所得y因为是矩阵运算的结果,第31层将其扁平化为一维数组。第33~35行重载训练函数fit。与其祖先LogicModel的(也是LineModel)fit函数相比,多了一个表示网络结构的参数hidden_layer_sizes。如前所述,这是一个元组,缺省值为(100,),意味着只有1个隐藏层,隐藏层含100个神经元。函数体内第34行调用自身的construct函数,构造网络结构layer_sizes,供调用拟合函数F时使用。第35行调用祖先LogicModel的fit函数完成训练。
第36~37用Regression类和MLPModel类联合构成用于预测的多层感应模型类MLPRegressor。
理论上,只要给定足够多的隐藏层和层内所含神经元,多层感应模型能拟合任意函数。
例1 用MLPRegressor对象拟合函数 y = x 2 y=x^2 y=x2。
解:先构造训练数据:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
np.random.seed(2023)
x = uniform.rvs(-1, 2, 50)
y = (x**2)
plt.scatter(x, y)
plt.show()
第5行产生50个服从均匀分布 U ( 0 , 1 ) U(0,1) U(0,1)的随机数值,赋予x。第6行计算x的平方赋予y。第7行绘制 ( x , y ) (x,y) (x,y)散点图。

用仅含一个隐藏层,隐藏层中包含3个神经元的多层感应器拟合 y = x 2 y=x^2 y=x2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
.random.seed(2023)
x = uniform.rvs(-1, 2, 50)
y = (x**2)
nnw = MLPRegressor()
nnw.fit(x,y,hidden_layer_sizes = (3,))
yp, acc = nnw.test(x, y)
plt.scatter(x, yp)
plt.show()
print('1隐藏层含3个神经元网络拟合均方根误差%.4f'%acc)
前5行与前同。第6行创建MLPRegressor类对象nnw。第7行用x,y训练nnw为含1个隐藏层,隐藏层含3个神经元的神经网络。第8行调用nnw的test函数,用返回的yp绘制 ( x , y p ) (x,y_p) (x,yp)散点图。

训练中...,稍候
726次迭代后完成训练。
1隐藏层含3个神经元网络拟合均方根误差0.0238
用含两个隐藏层,分别包含7个、3个神经元的多层感应器拟合 y = x 2 y=x^2 y=x2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform
.random.seed(2023)
x = uniform.rvs(-1, 2, 50)
y = (x**2)
nnw = MLPRegressor()
nnw.fit(x, y, hidden_layer_sizes = (7, 3))
yp, acc = nnw.test(x,y)
plt.scatter(x, yp)
plt.show()
print('2隐藏层含各7,3个神经元网络拟合方根误差%.4f'%acc)
与上一段代码比较,仅第8行训练nnw的网络换成两个隐藏层,分别包含7个、3个神经元的多层感应器。运行程序,输出

训练中...,稍候
1967次迭代后完成训练。
2隐藏层含各7,3个神经元网络拟合方根误差0.0053
比前一个显然拟合得更好,但也付出了计算时间的代价。
Say good bye, 2023.
相关文章:

最优化方法Python计算:无约束优化应用——神经网络回归模型
人类大脑有数百亿个相互连接的神经元(如下图(a)所示),这些神经元通过树突从其他神经元接收信息,在细胞体内综合、并变换信息,通过轴突上的突触向其他神经元传递信息。我们在博文《最优化方法Python计算:无约…...

Spring Data Redis对象缓存序列化问题
相信在项目中,你一定是经常使用 Redis ,那么,你是怎么使用的呢?在使用时,有没有遇到同我一样,对象缓存序列化问题的呢?那么,你又是如何解决的呢? Redis 使用示例 添加依…...

自动驾驶代客泊车AVP巡航规划详细设计
目 录 巡航规划详细设计... 1 修改记录... 2 目 录... 3 1 背景... 5 2 系统环境... 6 2.1 巡航规划与其它模块联系... 6 2.2 巡航规划接口说明... 6 3 规划模块设计... 9 3.1 巡航规划架构图... 9 3.2 预处理... 10 3.3 Planner. 10 3.3.1 Geometry planner. 10 …...
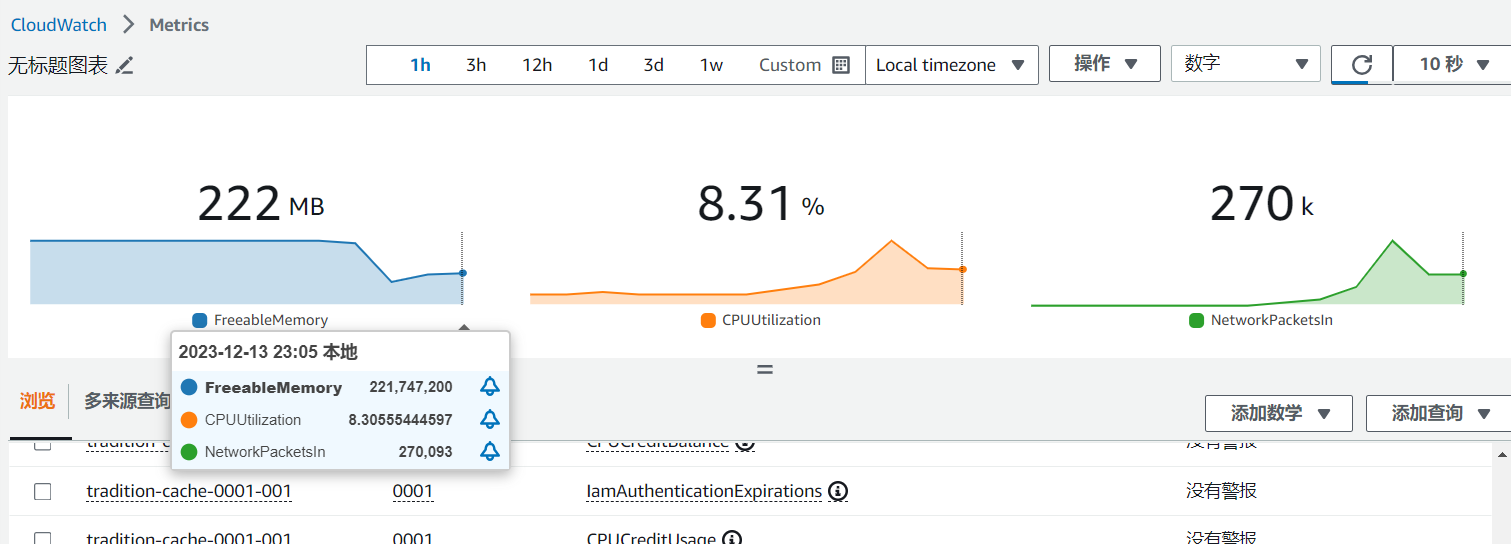
亚马逊云科技 re:Invent 2023 产品体验:亚马逊云科技产品应用实践 国赛选手带你看 Elasticache Serverless
抛砖引玉 讲一下作者背景,曾经参加过国内世界技能大赛云计算的选拔,那么在竞赛中包含两类,一类是架构类竞赛,另一类就是 TroubleShooting 竞赛,对应的分别为亚马逊云科技 GameDay 和亚马逊云科技 Jam,想必…...

Flink on K8S集群搭建及StreamPark平台安装
1.环境准备 1.1 介绍 在使用 Flink&Spark 时发现从编程模型, 启动配置到运维管理都有很多可以抽象共用的地方, 目前streampark提供了一个flink一站式的流处理作业开发管理平台, 从流处理作业开发到上线全生命周期都做了支持, 是一个一站式的流出来计算平台。 未来spark开…...

SpringBoot如何优雅的处理免登录接口
在项目开发过程中,会有很多API接口不需要登录就能直接访问,比如公开数据查询之类的 ~ 常规处理方法基本是 使用拦截器或过滤器,拦截需要认证的请求路径。在拦截器中判断session或token信息,如果存在则放行,否则跳转到…...

元旦档首日票房超4.69亿,“下雪场尴尬”上热搜!
哇塞,元旦假期终于来啦!🎉在这个喜庆的时刻,电影院也热闹非凡,据猫眼专业版数据显示,截至12月30日,2023年元旦档首日票房竟然超过了4.69亿!这简直是个天文数字啊!&#x…...

CentOS系统中设置IP地址的方式和存在的问题
在CentOS系统中设置IP地址通常涉及以下步骤: 打开网络接口配置文件: 使用文本编辑器(如vi、nano或emacs)打开 /etc/sysconfig/network-scripts/ifcfg-eth0 文件。这里的"eth0"是网卡的名称,如果你的系统中有…...
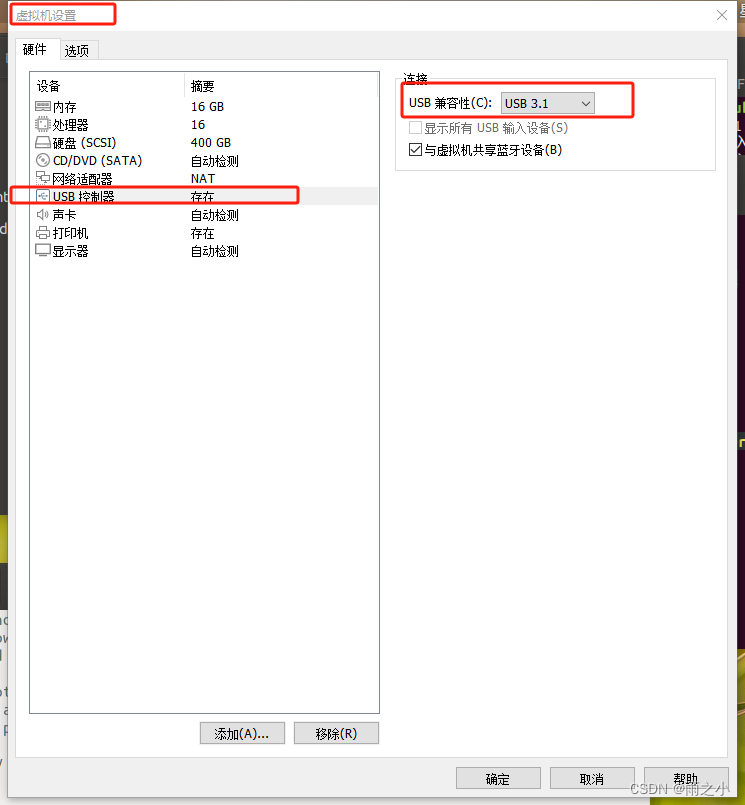
使用vmware,在ubuntu18.04中使用笔记本的摄像头
步骤1:在windows中检查相机状态 win10系统中,在左下的搜索栏,搜索“相机”,点击进入即可打开相机,并正常显示图像。 注意:如果相机连接到了虚拟机,则不能显示正常。 步骤2:在ubuntu…...

中间件系列 - Redis入门到实战(高级篇-分布式缓存)
前言 学习视频: 黑马程序员Redis入门到实战教程,深度透析redis底层原理redis分布式锁企业解决方案黑马点评实战项目 中间件系列 - Redis入门到实战 本内容仅用于个人学习笔记,如有侵扰,联系删除 学习目标 Redis持久化Redis主从…...
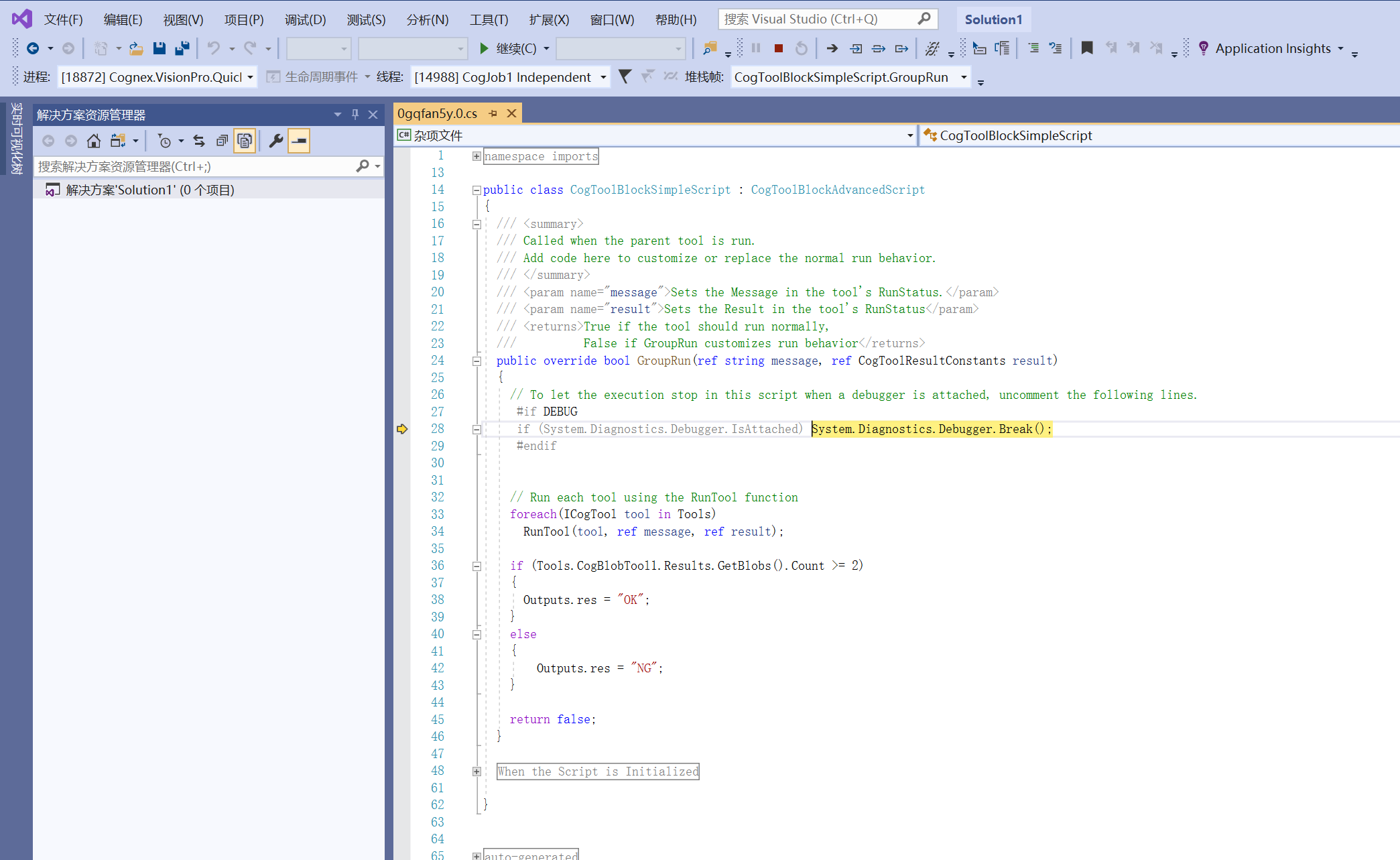
使用Visual Studio调试VisionPro脚本
使用Visual Studio调试VisionPro脚本 方法一 : 修改项目文件 csproj步骤: 方法二 : Visual Studio附加功能步骤: 方法一 : 修改项目文件 csproj 步骤: 开启VisionPro脚本调试功能 创建一个VisionPro程序…...
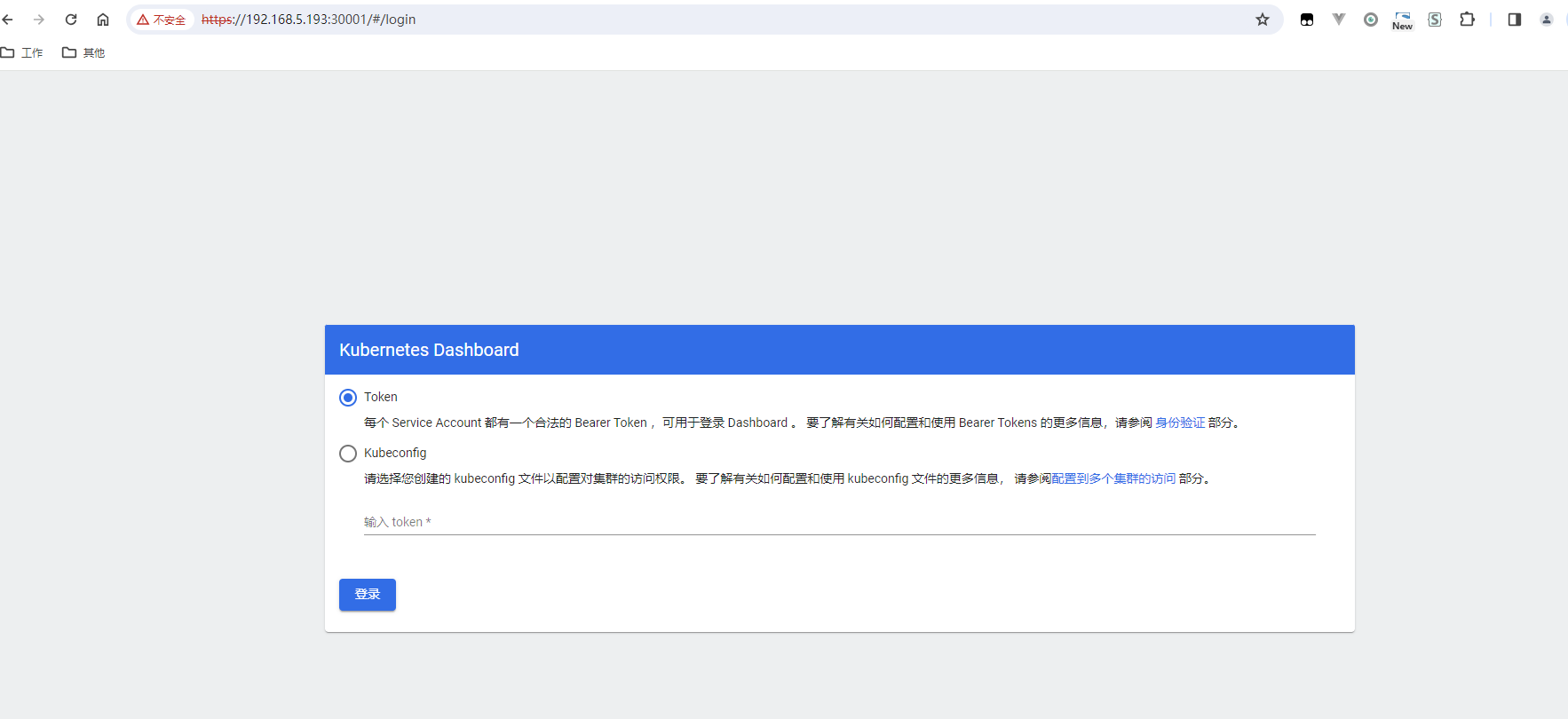
Ubuntu安装K8S的dashboard(管理页面)
原文网址:Ubuntu安装k8s的dashboard(管理页面)-CSDN博客 简介 本文介绍Ubuntu安装k8s的dashboard(管理页面)的方法。 Dashboard的作用有:便捷操作、监控、分析、概览。 相关网址 官网地址:…...
zookeeper之集群搭建
1. 集群角色 zookeeper集群下,有3种角色,分别是领导者(Leader)、跟随着(Follower)、观察者(Observer)。接下来我们分别看一下这三种角色的作用。 领导者(Leader): 事务请求(写操作)的唯一调度者和处理者,保…...

从0开始界面设计师 Qt Designer
QT程序界面的 一个个窗口、控件,就是像上面那样用相应的代码创建出来的。 但是,把你的脑海里的界面,用代码直接写出来,是有些困难的。 很多时候,运行时呈现的样子,不是我们要的。我们经常还要修改代码调整界…...
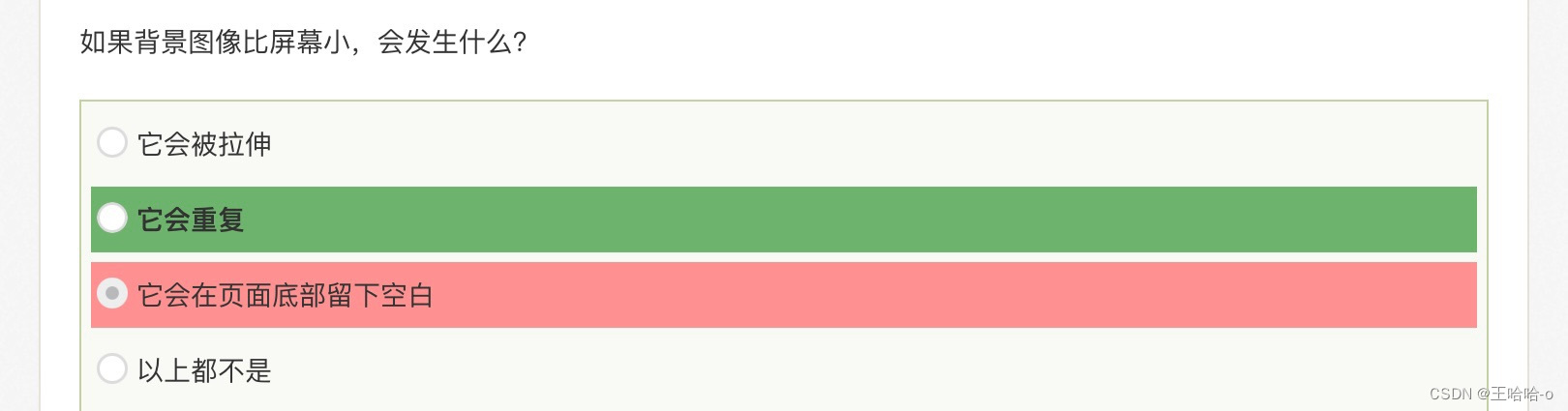
Html / CSS刷题笔记
WebKit是一个开源的浏览器引擎,它最初是由苹果公司开发的,并且被广泛用于Safari浏览器和其他基于WebKit的浏览器,比如Google Chrome的早期版本。它也是构建许多移动设备浏览器的基础。WebKit的主要功能是解析HTML和CSS,并将其渲染…...
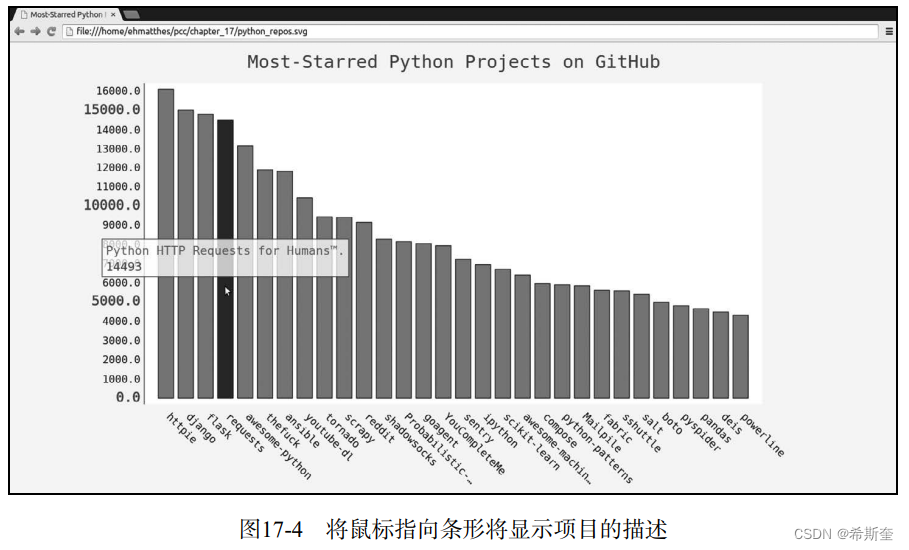
关于“Python”的核心知识点整理大全51
目录 17.2.2 添加自定义工具提示 bar_descriptions.py 17.2.3 根据数据绘图 python_repos.py 17.2.4 在图表中添加可单击的链接 python_repos.py 17.3 Hacker News API hn_submissions.py 17.4 小结 往期快速传送门👆(在文章最后)&a…...
Termius for Mac/Win:一站式终端模拟器、SSH 和 SFTP 客户端软件的卓越选择
随着远程工作和云技术的普及,对于高效安全的远程访问和管理服务器变得至关重要。Termius,一款强大且易用的终端模拟器、SSH 和 SFTP 客户端软件,正是满足这一需求的理想选择。 Termius 提供了一站式的解决方案,允许用户通过单一平…...
vr体验馆用什么软件计时计费,如遇到停电软件程序如何恢复时间
vr体验馆用什么软件计时计费,如遇到停电软件程序如何恢复时间 一、软件程序问答 如下图,软件以 佳易王vr体验馆计时计费软件V17.9为例说明 1、软件如何计时间? 点击相应编号的开始计时按钮即可 2、遇到停电再打开软件时间可以恢复吗&…...

HTML---JavaScript基础
文章目录 目录 文章目录 本章目标 一.JavaScript基础 概述 特点 JavaScript 基本机构 语法 网页中引用JavaScript的方式 二. JavaScript核心语法 变量 编辑 数据类型 数组 练习 本章目标 掌握JavaScript的组成掌握JavaScript的基本语法会定义和使用函数会使用工具进行…...

2023年03月17日_微软和谷歌办公AI的感慨
2023年3月17日 最近这个科技圈的消息 有点爆炸的让人应接不暇了 各种大公司简直就是神仙打架 你从来没有见过这么密集的 这么高频的产品发布 昨天微软是发布了Office 365 Copilot 在里边提供了大量的AI的功能 然后谷歌呢也发布了这个Google Workspace AI 也是跟365 Cop…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
