离散数学笔记(1)命题逻辑
文章目录
- 1.命题符号化及联结词
- 基本概念
- 本节题型
- 2.命题公式及分类
- 基本概念
- 本节题型
1.命题符号化及联结词
基本概念
命题的定义:能够判断真假的陈述句称为命题。
备注:感叹句、疑问句、祈使句和类似于x+y>5之类真值不唯一的句子都不是命题。
真值的真假性:判断正确的命题的真值为真,被称为真命题;判断错误的命题的真值为假,被称为假命题。因此又可以说命题是具有唯一真值的陈述句。常用1表示真命题,0表示假命题。
备注:命题的真假性可能目前是不确定的,但是一定存在且唯一。
简单命题(原子命题):不能分解成更简单的句子的命题被称为简单命题。由于简单命题的真值是确定的,因此也被称为命题常项或命题常元。
命题符号化:用小写的英文字母表示简单命题,被称为命题符号化。
命题变元:真值可以变化的简单陈述句被称为命题变项或命题变元。注意命题变元不是命题。
复合命题:由简单命题用联结词联结而成的命题被称为复合命题。
联结词:
- 否定联结词:设p为任一命题。复合命题“非p”称为p的否定式,记作 ┐p。 ┐为否定联结词。
- 合取联结词:设p、q为两个命题。复合命题“p并且q”称作p和q的合取式,记作p∧q。p∧q为真当且仅当p和q都为真。
- 析取联结词:设p、q为两个命题。复合命题“p或q”称为p与q的析取式,记作p∨q。∨被称为析取联结词。p∨q为真当且仅当p与q中至少有一个为真。
备注:析取表示的是一种相容性的或运算,并非非此即彼。需要注意在使用排斥或时不能直接用析取式。
- 蕴含联结词:设p、q为两个命题。复合命题“如果p,则q”称作p与q的蕴含式,记作p→q,称p为蕴含式的前件,q为蕴含式的后件。→称作蕴含联结词。p→q为假当且仅当p为真且q为假。
p蕴含q的基本逻辑关系是:q是p的必要条件,或p是q的充分条件。
- 等价联结词:设p、q为两个命题。复合命题“p当且仅当q”称作p和q的等价式,记作p↔q。↔称为等价联结词。p↔为真当且仅当p和q真值相同。
联结词的运算优先级:否定>合取>析取>蕴含>等价。如果有括号需要先计算括号里的。
本节题型
- 判断一个句子是否是命题;
- 判断一个命题属于简单命题还是复合命题;
- 将命题符号化(带有各种联结词);
- 判断一个命题的真假性(带有各种联结关系);
2.命题公式及分类
基本概念
合项公式(命题公式/公式)的定义:
- 单个命题变项:单个命题变项是合式公式。
- 联结词短语:对一个或多个合式公式使用联结词进行联结,所得到的也是合式公式。要求联结的次数是有限次。
- 1和0:把1看作某个恒取1的公式的缩写,把0看作某个恒取0的公式的缩写。
命题公式的层次的定义:
- 若A是单个命题变项,则称A是0层公式。
- 当B是n层公式,且A=┐B时,A是n+1层公式。
- 当B、C分别是i层和j层公式,且max(i,j)=n。如果A=B∧C或A=B∨C或A=B→C或A=B↔C,则A是n+1层公式。
命题公式的真值:命题公式的真值往往是不确定的,只有对它的每个命题变项用指定的命题常项代替后,命题公式才会成为命题,其真值此时也会唯一确定。
命题公式的赋值:设A是一个命题公式,p1p2…pn为出现在A中的所有的命题变项,给p1,p2…pn指定一组真值,称为对A的一个赋值或解释。如果指定的一组值使A的值为真,则称这组值为A的成真复制;若使A的值为假,则称这组值为A的成假赋值。
真值表的概念:将某个命题公式的所有赋值情况下的取值列成表,称为该命题公式的真值表。
构造真值表的步骤:
- 找出命题公式中所含的所有命题变项p1,p2…pn(如果无下角标就按照字典顺序给出);
- 按照从低到高的顺序写出各个层次;
- 列出所有可能的赋值。从00…0(n位)开始,每次加一,直到11…1为止。
- 对应每个赋值,计算命题公式各个层次的值,直到最后计算出命题公式的值。
命题公式的分类:
- 重言式(永真式):在所有赋值下取值都为真的命题公式。
- 矛盾式(永假式):在所有赋值下取值都为假的命题公式。
- 可满足式:至少存在一组成真赋值的命题公式。
真值函数的概念:一个n(n≥1)阶笛卡尔积到{0,1}的函数被称为一个n元真值函数。
本节题型
- 命题公式的真值判断;
- 命题公式的类型判断;
相关文章:
命题逻辑)
离散数学笔记(1)命题逻辑
文章目录1.命题符号化及联结词基本概念本节题型2.命题公式及分类基本概念本节题型1.命题符号化及联结词 基本概念 命题的定义:能够判断真假的陈述句称为命题。 备注:感叹句、疑问句、祈使句和类似于xy>5之类真值不唯一的句子都不是命题。 真值的真假…...
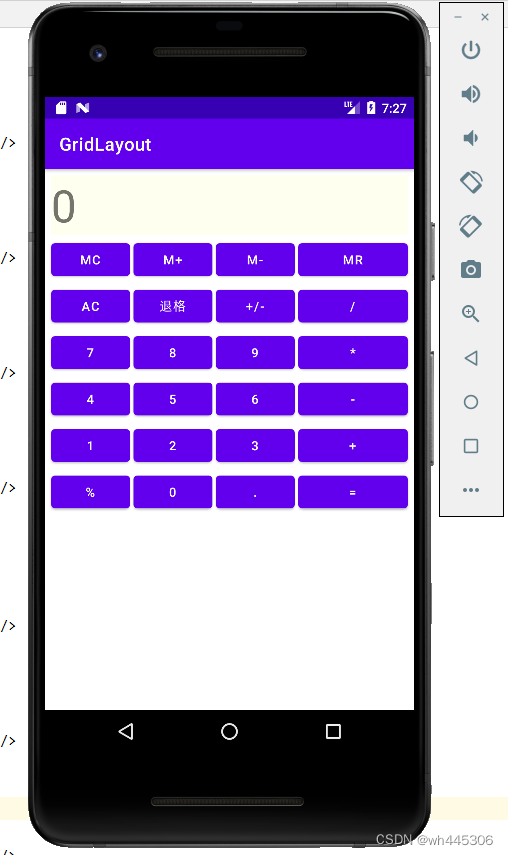
IDEA Android 网格布局(GridLayout)示例(计算器界面布局)
网格布局(GridLayout) 示例程序效果(实现类似vivo手机自带计算器UI) 真机和模拟器运行效果: 简述: GridLayout(网格布局)和TableLayout(表格布局)有类似的地方,通俗来讲可以理解为…...

【蓝桥杯嵌入式】拓展板之数码管显示
文章目录硬件电路连接方式函数实现文章福利硬件电路 通过上述原理图,可知拓展板上的数码管是一个共阴数码管,也就是说某段数码管接上高电平时,就会点亮。 上述原理图还给出一个提示,即:三个数码管分别与三个74HC59…...
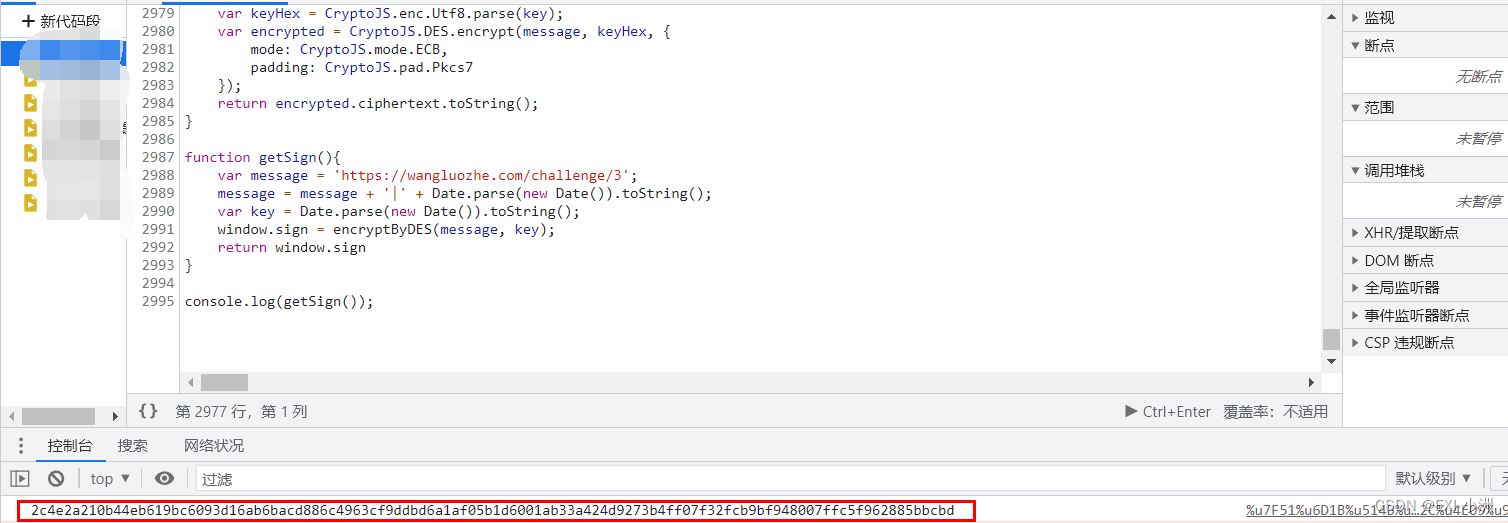
Web Spider案例 网洛克 第三题 AAEncode加密 练习(七)
声明 此次案例只为学习交流使用,抓包内容、敏感网址、数据接口均已做脱敏处理,切勿用于其他非法用途; 文章目录声明一、资源推荐二、逆向目标三、抓包分析 & 下断分析逆向3.1 抓包分析3.2 下断分析逆向拿到混淆JS代码3.3 AAEncode解决方…...
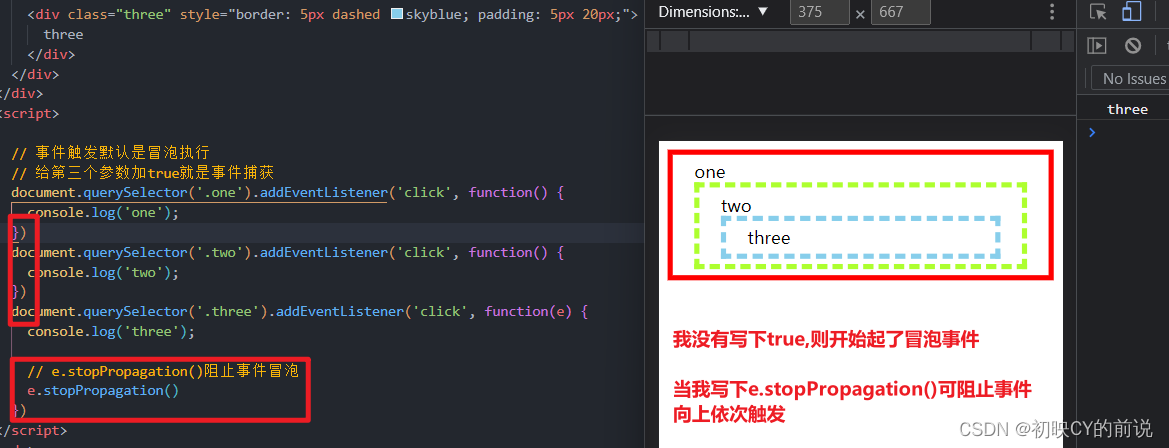
【javaScript面试题】2023前端最新版javaScript模块,高频24问
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:博主收集的关于javaScript的面试题 目录 一、2023javaScript面试题精选 1.js的数据类型…...

Hadoop集群启动从节点没有DataNode
一、问题背景 之前启动hadoop集群的时候都没有问题,今天启动hadoop集群的时候,从节点的DataNode没有启动起来。 二、解决思路 遇见节点起不来的情况,可以去看看当前节点的日志文件 我进入当前从节点的hadoop安装目录的Logs文件下去查看日…...
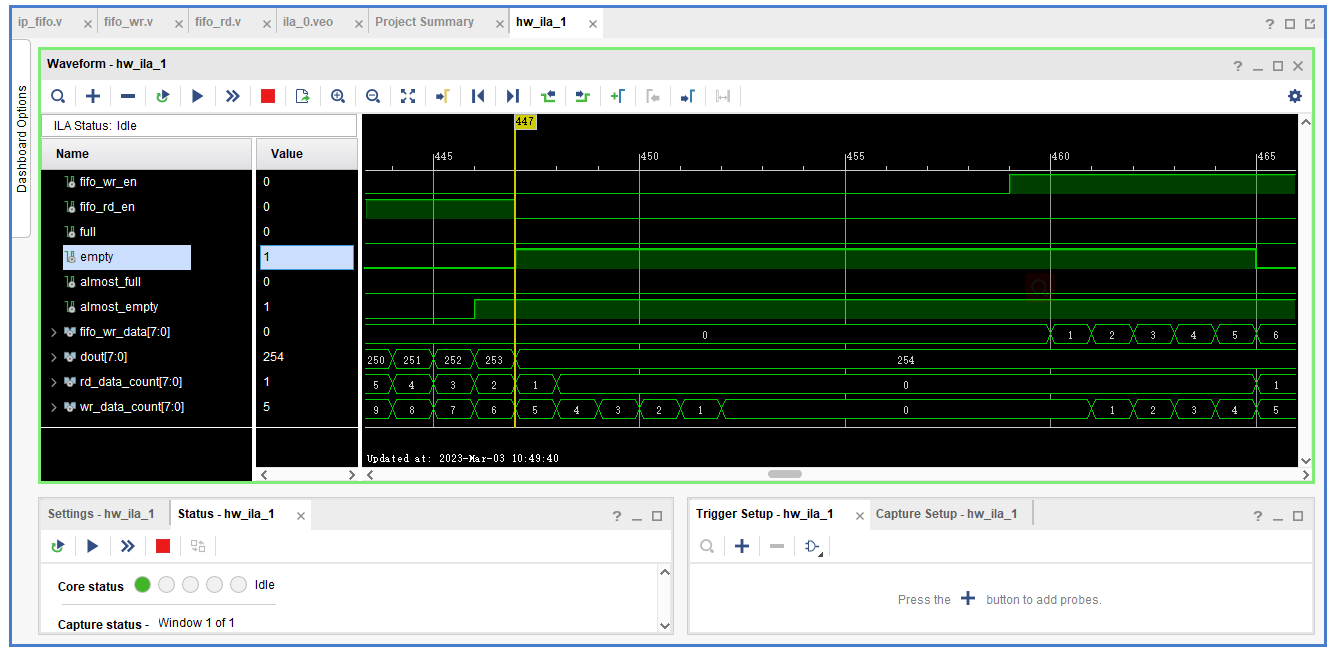
FIFO IP Core
FIFO IP Core 先进先出的缓存器常常被用于数据的缓存,或者高速异步数据交互(跨时钟信号传递)和RAM和ROM的区别是没有地址线,无法指定地址 写时钟(Write Clock Domain),读时钟写复位(wr_rst),读…...

从FPGA说起的深度学习(四)
这是新的系列教程,在本教程中,我们将介绍使用 FPGA 实现深度学习的技术,深度学习是近年来人工智能领域的热门话题。在本教程中,旨在加深对深度学习和 FPGA 的理解。用 C/C 编写深度学习推理代码高级综合 (HLS) 将 C/C 代码转换为硬…...
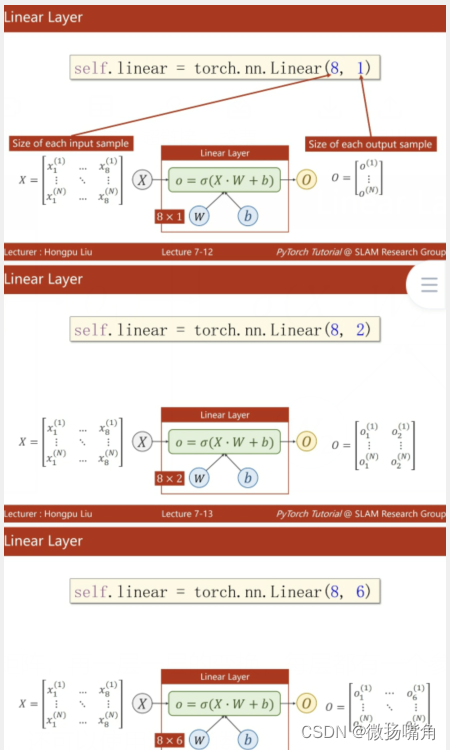
pytorch入门7--自动求导和神经网络
深度学习网上自学学了10多天了,看了很多大神的课总是很快被劝退。终于,遇到了一位对小白友好的刘二大人,先附上链接,需要者自取:https://b23.tv/RHlDxbc。 下面是课程笔记。 一、自动求导 举例说明自动求导。 torch中的…...

QT 之wayland 事件处理分析基于qt5wayland5.14.2
1. Qt wayland 初始化 接收鼠标/案件,触摸屏等事件事件 QWaylandNativeInterface : public QPlatformNativeInterface 在QWaylandNativeInterface 继承qpa 接口类QPlatformNativeInterface; 1.1 初始化鼠标: void *QWaylandNativeInterface::nativeR…...

【this 和 super 的区别】
在 Java 中,this 和 super 都是关键字,表示当前对象和父类对象。 this 关键字可以用于以下几种情况: 引用当前对象的成员变量,方法和构造方法,用于区分局部变量和成员变量重名的情况; 调用当前类的另外一…...
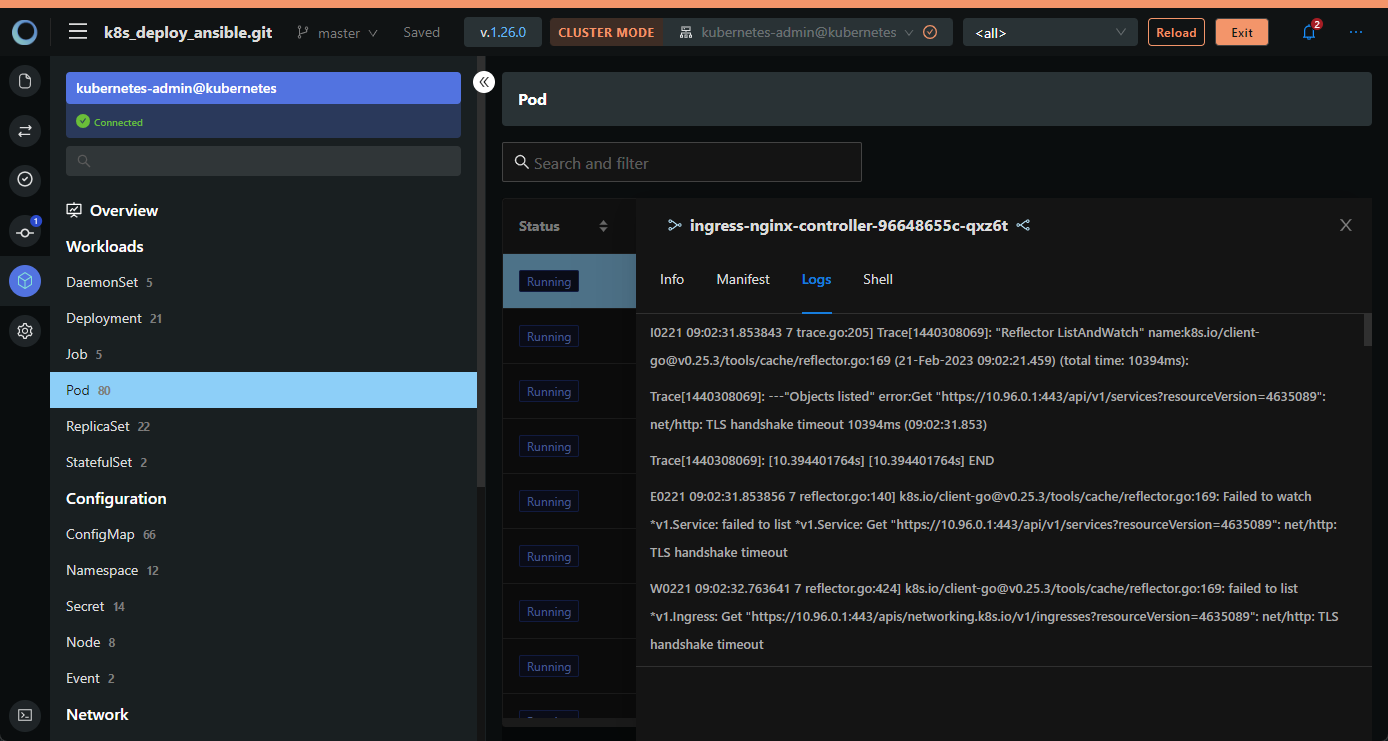
K8s:Monokle Desktop 一个集Yaml资源编写、项目管理、集群管理的 K8s IDE
写在前面 Monokle Desktop 是 kubeshop 推出的一个开源的 K8s IDE相关项目还有 Monokle CLI 和 Monokle Cloud相比其他的工具,Monokle Desktop 功能较全面,涉及 k8s 管理的整个生命周期博文内容:Monokle Desktop 下载安装,项目管理…...

自动化测试实战篇(8),jmeter并发测试登录接口,模拟从100到1000个用户同时登录测试服务器压力
首先进行使用jmeter进行并发测试之前就需要搞清楚线程和进程的区别还需要理解什么是并发、高并发、并行。还需要理解高并发中的以及老生常谈的,TCP三次握手协议和TCP四次握手协议**TCP三次握手协议指:****TCP四次挥手协议:**进入Jmeter&#…...

ATTCK v12版本战术实战研究—持久化(二)
一、前言前几期文章中,我们介绍了ATT&CK中侦察、资源开发、初始访问、执行战术、持久化战术的知识。那么从前文中介绍的相关持久化子技术来开展测试,进行更深一步的分析。本文主要内容是介绍攻击者在运用持久化子技术时,在相关的资产服务…...

python函数式编程
1 callable内建函数判断一个名字是否为一个可调用函数 >>> import math >>> x 1 >>> y math.sqrt >>> callable(x) False >>> callable(y) True 2 记录函数(文档字符串) >>> def square(x): …...

3.linux下安装mysql
1.安装前的环境准备 查看是否安装过mysql 首先检测Linux操作系统中是否安装了MySQL: # rpm -qa | grep -i mysql 卸载安装包 如果有信息出现,则进行删除,命令如下: # rpm -e --nodeps 包名 删除老版本mysql的开发头文件和…...

17、MySQL分库分表,原理实战
MySQL分库分表,原理实战 1.MyCAT分布式架构入门及双主架构1.1 主从架构1.2 MyCAT安装1.3 启动和连接1.4 配置文件介绍2.MyCAT读写分离架构2.1 架构说明2.2 创建用户2.3 schema.xml2.4 连接说明2.5 读写测试2.6 当前是单节点3.MyCAT高可用读写分离架构3.1 架构说明3.3 schema.xm…...
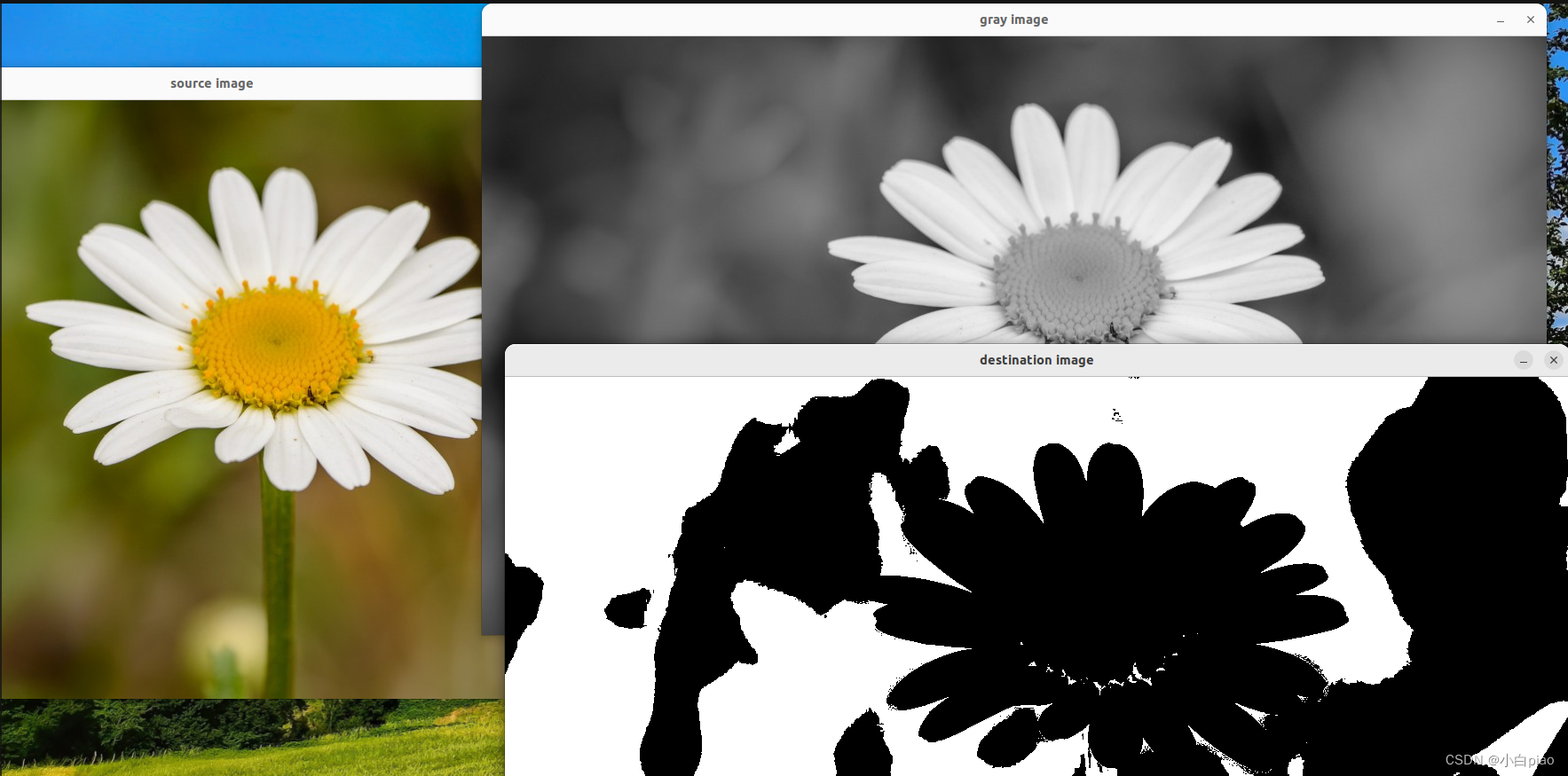
【C++的OpenCV】第九课-OpenCV图像常用操作(六):图像形态学-阈值的概念、功能及操作(threshold()函数))
目录一、阈值(thresh)的概念二、阈值在图形学中的用途三、阈值的作用和操作3.1 在OpenCV中可以进行的阈值操作3.2 操作实例3.2.1 threshold()函数介绍3.2.2 实例3.2.3 结果上节课的内容(作者还是鼓励各位同学按照顺序进行学习哦)&…...

[Java代码审计]—MCMS
环境搭建 MCMS 5.2.4:https://gitee.com/mingSoft/MCMS/tree/5.2.4/利用 idea 打开项目 创建数据库 mcms,导入 doc/mcms-5.2.8.sql 修改 src/main/resources/application-dev.yml 中关于数据库设置参数 启动项目登录后台 http://localhost:8080/ms/l…...
》面试题 01.08. 零矩阵)
《程序员面试金典(第6版)》面试题 01.08. 零矩阵
题目描述 编写代码,移除未排序链表中的重复节点。保留最开始出现的节点。 示例1: 输入:[1, 2, 3, 3, 2, 1] 输出:[1, 2, 3] -示例2: 输入:[1, 1, 1, 1, 2] 输出:[1, 2] 提示: 链表长度在[0, 20000]范…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
