模式识别与机器学习-SVM(带软间隔的支持向量机)
SVM(带软间隔的支持向量机)
- 软间隔思想的由来
- 软间隔的引入
谨以此博客作为复习期间的记录。
软间隔思想的由来
在上一篇博客中,回顾了线性可分的支持向量机,但在实际情况中,很少有完全线性可分的情况,大部分线性可分的情况都是整体线性可分,个别样本点无法线性分割开。因此就要避免这极个别样本点对分割平面产生的影响。
线性可分支持向量机
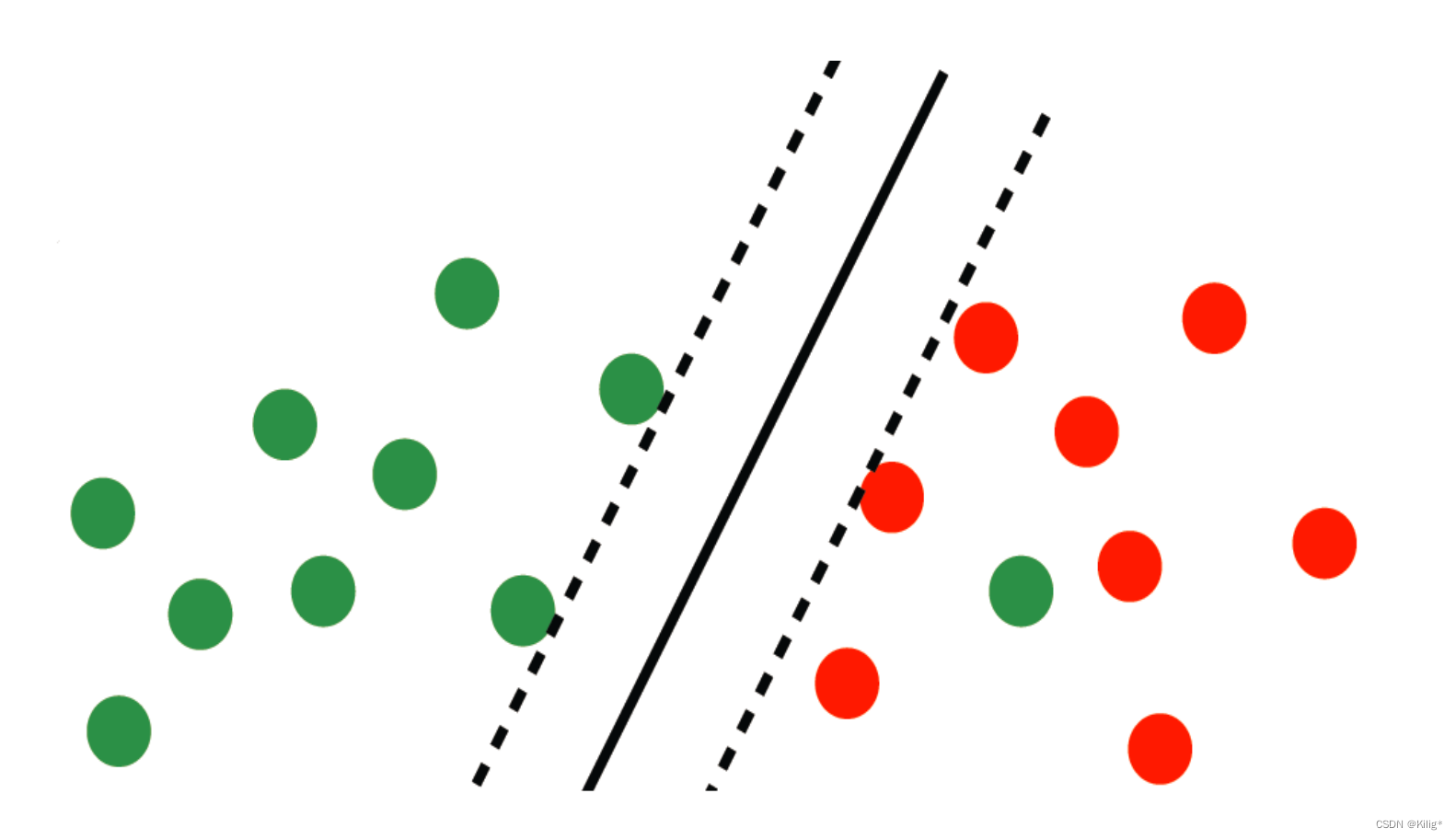
软间隔的引入
在分类过程中,允许极个别数据点“越界”,如何在目标函数中体现这一点呢?
软间隔支持向量机(Soft Margin Support Vector Machine)的数学形式可以通过修改支持向量机(SVM)的优化目标函数和约束条件来实现。软间隔允许一些数据点越界,引入了松弛变量来处理这些点。
首先,我们考虑软间隔的目标函数和约束条件:
-
目标函数:
最小化目标函数,同时考虑间隔的最大化和误分类点的惩罚,即:
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i \min_{\mathbf{w}, b, \boldsymbol{\xi}} \frac{1}{2}\|\mathbf{w}\|^2 + C \sum_{i=1}^{N} \xi_i w,b,ξmin21∥w∥2+Ci=1∑Nξi
这里 w \mathbf{w} w 是超平面的法向量, b b b 是截距, ξ \boldsymbol{\xi} ξ 是松弛变量, C > 0 C > 0 C>0 是一个超参数,用于控制对误分类点的惩罚程度。 -
约束条件:
考虑函数间隔大于等于 1 的约束条件,以及松弛变量 ξ \boldsymbol{\xi} ξ 的非负性约束:
y i ( w ⋅ x i + b ) ≥ 1 − ξ i , i = 1 , 2 , … , N ξ i ≥ 0 , i = 1 , 2 , … , N \begin{align*} & y_i(\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 - \xi_i, \quad i = 1, 2, \dots, N \\ & \xi_i \geq 0, \quad i = 1, 2, \dots, N \end{align*} yi(w⋅xi+b)≥1−ξi,i=1,2,…,Nξi≥0,i=1,2,…,N
线性支持向量机学习算法
输入: 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\left\{\left(x_1, y_1\right),\left(x_2, y_2\right), \cdots,\left(x_N, y_N\right)\right\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中, x i ∈ X = R n , y i ∈ x_i \in \mathcal{X}=\mathbf{R}^n, y_i \in xi∈X=Rn,yi∈ Y = { − 1 , + 1 } , i = 1 , 2 , ⋯ , N \mathcal{Y}=\{-1,+1\}, \quad i=1,2, \cdots, N Y={−1,+1},i=1,2,⋯,N;
输出: 分离超平面和分类决策函数.
(1) 选择惩罚参数 C > 0 C>0 C>0, 构造并求解凸二次规划问题
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , ⋯ , N \begin{aligned} \min _\alpha & \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ \text { s.t. } & \sum_{i=1}^N \alpha_i y_i=0 \\ & 0 \leqslant \alpha_i \leqslant C, \quad i=1,2, \cdots, N \end{aligned} αmin s.t. 21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαii=1∑Nαiyi=00⩽αi⩽C,i=1,2,⋯,N
求得最优解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^*=\left(\alpha_1{ }^*, \alpha_2{ }^*, \cdots, \alpha_N{ }^*\right)^{\mathrm{T}} α∗=(α1∗,α2∗,⋯,αN∗)T.
(2) 计算 w ∗ = ∑ i = 1 N α i ∗ y i x i w^*=\sum_{i=1}^N \alpha_i^* y_i x_i w∗=∑i=1Nαi∗yixi
选择 α ∗ \alpha^* α∗ 的一个分量 α j ∗ \alpha_j{ }^* αj∗ 适合条件 0 < α j ∗ < C 0<\alpha_j^*<C 0<αj∗<C, 计算
b ∗ = y j − ∑ i = 1 N y i α i ∗ ( x i ⋅ x j ) b^*=y_j-\sum_{i=1}^N y_i \alpha_i^*\left(x_i \cdot x_j\right) b∗=yj−i=1∑Nyiαi∗(xi⋅xj)
(3) 求得分离超平面
w ∗ ⋅ x + b ∗ = 0 w^* \cdot x+b^*=0 w∗⋅x+b∗=0
分类决策函数:
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^* \cdot x+b^*\right) f(x)=sign(w∗⋅x+b∗)
相关文章:

模式识别与机器学习-SVM(带软间隔的支持向量机)
SVM(带软间隔的支持向量机) 软间隔思想的由来软间隔的引入 谨以此博客作为复习期间的记录。 软间隔思想的由来 在上一篇博客中,回顾了线性可分的支持向量机,但在实际情况中,很少有完全线性可分的情况,大部分线性可分…...

CentOS 7 firewalld+ipset+定时任务防御ssh暴力破解——筑梦之路
对于暴露在公网上的linux服务器,很容易被暴力破解登陆,为了增强服务器的安全性,因此对于ssh安全加固是很有必要的,这里主要介绍centos7 系统如何使用ipsetfirewalld定时任务来对ssh服务进行安全加固。 定义firewalld ipset fire…...

ElasticSearch的RestClient结合Sniffer提高可用性
一、背景 由于要安装分词器插件,所以需要重启ElasticSearch集群以使得新安装的插件生效 但是在重启集群的过程中,服务端代码却出现了大量错误,如下所示 java.net.ConnectException: Connection refused at org.elasticsearch.client.R…...

【网络面试(2)】DNS原理-域名和IP地址的查询转换
从上一篇博客我们得知浏览器是如何生成了HTTP消息了,但是浏览器作为应用程序,是不具备向网络中发送请求的能力,而是需要委托给操作系统的内核协议栈来发送请求。在委托协议栈之前,浏览器还要做的一件事情就是将域名转换为IP地址。…...

【PHP】函数array_intersect、array_diff:从数组中取出、去除指定的几个键值
1.从数组中取出 :array_intersect 要从数组中取出指定的几个键值,可以使用 array_intersect_key 函数。以下是一个示例: $array [name > John,age > 30,email > johnexample.com,city > New York ];$keys [name, email];$resu…...

【华为机试】2023年真题B卷(python)-冠亚军排名-奖牌榜排名
一、题目 题目描述: 2012伦敦奥运会即将到来,大家都非常关注奖牌榜的情况,现在我们假设奖牌榜的排名规则如下. 1.首先gold medal数量多的排在前面 2.其次silver medal数量多的排在前面 3.然后bronze medal数量多的排在前面 4.若以上三个条…...

MyBatisPlus之逻辑删除
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 MyBatisPlus之逻辑删除 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、什么是逻辑删…...
在macOS中搭建.NET MAUI开发环境
文章目录 准备安装扩展安装 .NET安装工作负载安装 Xcode 命令行工具调试安卓应用安装 JDK安装 Android SDK 安装 Android 模拟器安装模拟器安装镜像创建虚拟机 同意许可条款创建 MAUI 项目调试 MAUI 应用切换调试目标 参考资料 准备 一台 macOS Monterey 以上的电脑安装 XCode…...
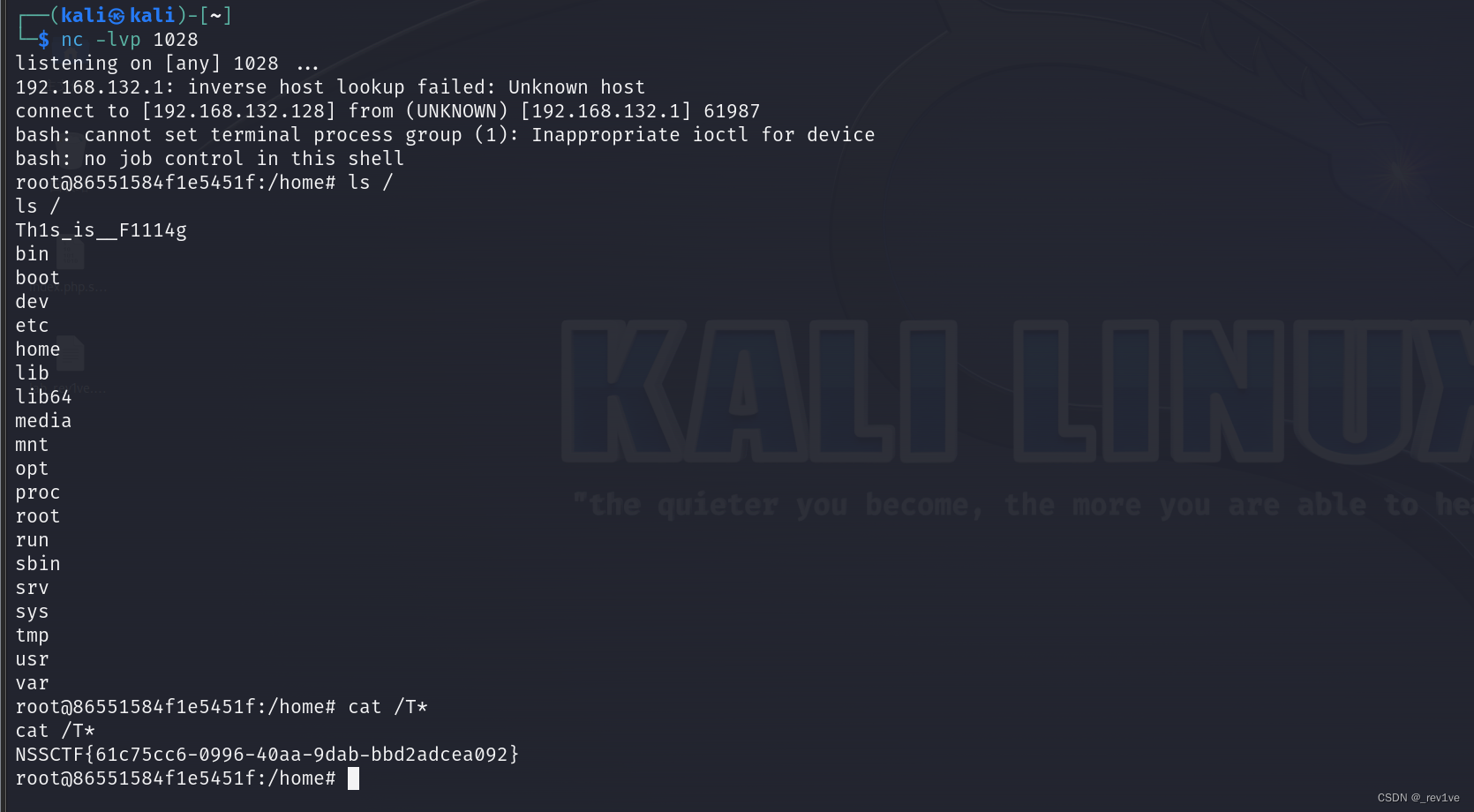
[NCTF 2022]calc
[NCTF 2022]calc 考点:python环境变量注入 打开题目,F12有hint 访问一下得到源码 app.route("/calc",methods[GET]) def calc():ip request.remote_addrnum request.values.get("num")log "echo {0} {1} {2}> ./tmp/log…...
【pandas_不重复项计数】
听说WPS没有非重复项计数的功能,而office需要添加到数据模型之后,才可以使用该功能。而用pandas,既可以对重复项计数,又可以对非重复项计数。 # 使用提醒: # 1. xbot包提供软件自动化、数据表格、Excel、日志、AI等功能 # 2. pack…...
菜鸟学习vue3笔记-vue hooks初体验
import { ref } from "vue"; export default function () {let a1 ref(1);let a2 ref(5);let c ref(0);function add() {a1.value;a2.value;}return {add,a1,a2,c,}; }<template><div><p>第一个数字{{ a1 }}</p><p>第二个数字{{ a2…...

81 使用DFS和BFS解机器人的运动范围
问题描述:地上有一个m行n列的方格,从坐标[0,0]到坐标[m-1,n-1].一个机器人从坐标[0,0]的格子开始移动,他每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。 public int numB…...
vue-springboot基于JavaWeb的家装一体化商城平台guptn
针对用户需求开发与设计,该技术尤其在各行业领域发挥了巨大的作用,有效地促进了家装一体化的发展。然而,由于用户量和需求量的增加,信息过载等问题暴露出来,为改善传统线下管理中的不足,本文将提出一套基于…...

.NET进阶篇06-async异步、thread多线程2
知识须要不断积累、总结和沉淀,思考和写做是成长的催化剂web 内容目录 1、线程Thread 一、生命周期 二、后台线程 三、静态方法 1.线程本地存储 2.内存栅栏 四、返回值 2、线程池ThreadPool 一、工做队列 二、工做线程和IO线程 三、和Thread区别 四、定时器 1、线…...

java 方法
方法: 什么是方法,有什么用? 方法(英语单词:method)是可以完成某个特定功能的并且可以被重复利用的代码片段。 在 C 语言中,方法被称为“函数”。在 java 中不叫函数,叫做方法。 方法…...
HarmonyOS 组件通用属性之通用事件 文档参数讲解(点击事件)
我们组件中 会有很多通用的信息和方法 那么 首先 我们看通用事件 通用事件中 最常用的就是我们的点击事件 比如说 我们之前常写的 组件.onClick(()>{//事件逻辑 })但是 我们之前 都没有用它接参数 我们可以这样 Button("跳转").onClick((ewat: ClickEvent)>…...

毕业设计之开题报告
终于轮到我来写开题报告了,呃呃呃呃呃,目前有点难产了。想做的东西是关于区块链的后端设计实现,但是因为是完全原创之前没有类似的项目能去参考,所以其实有点慌的。 框架梳理 这是我们开题报告的要求: 包括题目研究的…...

【数据结构】详细剖析线性表
顺序表与链表的比较 导言一、线性表二、线性表的存储结构三、顺序表和链表的相同点四、顺序表与链表之间的差异五、存储结构的选择六、静态顺序表的基本操作七、无头结点单链表的基本操作结语 导言 大家好,很高兴又和大家见面啦!!࿰…...

通过数字证书对PDF电子文件进行数字签名/盖章
以下代码详细说明如何使用数字证书对PDF电子文件进行数字签名/盖章。PDF文件签署主要传递PDF文件,数字证书信息,签章图片3个信息。代码中需要的文件、数字证书、签章图片可访问开放签电子签章开源系统详细了解系统的实现与效果。也可通过gitee开源社区下…...

2007~2016 年税调经纬度及其所处的省市区县乡镇数据
之前给大家分享过一份税调企业经纬度及其所处的省市区县数据: 2007~2016 年税调企业地理信息数据(含经纬度及其所处的省市区县):https://rstata.duanshu.com/#/course/76d38022cd004b09b2aa09647936beb0 最近有培训班的小伙伴提出是否能根据税调企业经纬度来判断其所属的乡…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
