【Rust】一文讲透Rust中的PartialEq和Eq
前言
本文将围绕对象:PartialEq和Eq,以及PartialOrd和Ord,即四个Rust中重点的Compare Trait进行讨论并解释其中的细节,内容涵盖理论以及代码实现。
在正式介绍PartialEq和Eq、以及PartialOrd和Ord之前,本文会首先介绍它们所遵循的数学理论,也就是相等关系。
文章主要分三大部分,第一部分是第1节,讨论的是数学中的相等关系;第二部分是第2~5节,主要讨论PartialEq和Eq;第三部分是第6节,主要讨论PartialOrd和Ord。内容描述可能具有先后顺序,建议按章节顺序阅读。
声明
本文内容来自作者个人的学习成果总结及整理,可能会存在因个人水平导致的表述错误,欢迎并感谢读者指正!
- 作者:Leigg
- 首发地址:https://github.com/chaseSpace/rust_practices/blob/main/blogs/about_eq_ord_trait.md
- CSDN:https://blog.csdn.net/sc_lilei/article/details/129322616
- 发布时间:2023年03月03日
- License:CC-BY-NC-SA 4.0 (转载请注明作者及来源)
1. 数学中的相等关系
在初中数学中,会介绍到什么是相等关系(也叫等价关系),相等关系是一种基本的二元关系,它描述了两个对象之间的相等性质。它必须满足如下三个性质:
- 自反性(反身性):自己一定等于自己,即
a=a; - 对称性:若有
a=b,则有b=a; - 传递性:若有
a=b和b=c,则有a=c;
也就是说,满足这三个性质才叫满足(完全)相等关系。这很容易理解,就不过多解释。
1.1 部分相等关系
对于简单的整数类型、字符串类型,我们可以说它们具有完全相等关系,因为它们可以全方位比较(包含两个维度,第一个是类型空间中的任意值,第二个是每个值的任意成员属性), 但是对于某些类型就不行了,这些类型总是不满足其中一个维度
。下面一起来看看:
以字符串为例,全方位比较的是它的每个字节值以及整个字符串的长度。
0. 浮点数类型
在浮点数类型中有个特殊的值是NaN(Not-a-number),这个值与任何值都不等(包括自己),它直接违背了自反性。这个时候,我们就需要为浮点数定义一种部分相等关系,这主要是为了比较非NaN浮点数。
NaN定义于IEEE 754-2008标准的5.2节“特殊值”(Special Values)中,除了NaN,另外两个特殊值是正无穷大(+infinity)、负无穷大(-infinity),不过这两个值满足自反性。
除了浮点数类型,数学中还有其他类型也不具有通常意义上的全等关系,比如集合类型、函数类型。
1. 集合类型
假设有集合A={1,2,3}、B={1,3,2},那么此时A和B是相等还是不相等呢?这就需要在不同角度去看待,当我们只关注集合中是否包含相同的元素时, 可以说它们相等,当我们还要严格要求元素顺序一致时,它们就不相等。
在实际应用中,由我们定义(Impl)了一种集合中的特殊相等关系,称为"集合的相等",这个特殊关系(实现逻辑)中,我们只要求两个集合的元素相同,不要求其他。
2. 函数类型
首先从浮点数的NaN角度来看函数,假设有函数A=f(x)、B=f(y),若x=y,那显然A的值也等于B,但是如果存在一个参数z是无意义的呢,意思是f(z)是无结果的或结果非法,那么此时可以说f(z)等于自身吗?
那显然是不行的。这个例子和浮点数的例子是一个意思。
然后从集合类型的角度再来看一次函数,假设有函数A=f(x)、B=g(x),注意是两个不同的函数,当二者给定一个相同输入x产生相同结果时,此时f(x)和g(x)是相等还是不等呢?
与集合类似,实际应用中,这里也是由我们定义(Impl)了一种函数中的特殊相等关系,称为函数的相等。这个特殊关系(实现逻辑)中,我们只要求两个函数执行结果的值相同,不要求函数执行过程相同。
1.2 部分相等与全相等的关系
部分相等是全相等关系的子集,也就是说,如果两个元素具有相等关系,那它们之间也一定有部分相等关系。这在编程语言中的实现也是同样遵循的规则。
1.3 小结
数学中定义了(全)相等关系(等价关系)的三大性质,分别是自反性、对称性和传递性;但某些数据类型中的值或属性违背了三大性质,就不能叫做满足全相等关系, 此时只能为该类型实现部分相等关系。
在部分相等关系中,用于比较的值也是满足三大性质的,因为此时我们排除了那些特殊值。另外,部分相等是全相等关系的子集。
2. 编程与数学的关系
数学是一门研究数据、空间和变化的庞大学科,它提供了一种严谨的描述和处理问题的方式,而编程则是将问题的解决方法转化为计算机程序的过程,可以说,数学是问题的理论形式, 编程则是问题的代码形式,编程解决问题的依据来自数学。
所以说,编程语言的设计中也是大量运用了数学概念与模型的,本文关注的相等关系就是一个例子。
在Rust库中的PartialEq的注释文档中提到了partial equivalence relations 即部分相等关系这一概念,并且同样使用了浮点数的特殊值NaN来举例说明。
Eq的注释文档则是提到了equivalence relations,并且明确说明了,对于满足Eqtrait的类型,是一定满足相等关系的三大性质的。
3. PartialEq
3.1 trait定义
Rust中的PartialEq的命名明确地表达了它的含义,但如果我们忘记了数学中的相等关系,就肯定会对此感到疑惑。先来看看它的定义:
pub trait PartialEq<Rhs: ?Sized = Self> {fn eq(&self, other: &Rhs) -> bool;fn ne(&self, other: &Rhs) -> bool {!self.eq(other)}
}
在这个定义中,可以得到三个基本信息:
- 这个trait包含2个方法,eq和ne,且ne具有默认实现,使用时开发者只需要实现eq方法即可(库文档也特别说明,若没有更好的理由,则不应该手动实现ne方法);
- PartialEq绑定的Rhs参数类型是
?Size,即包括动态大小类型(DST)和固定大小类型(ST)类型(Rhs是主类型用来比较的类型); - Rhs参数提供了默认类型即
Self(和主类型一致),但也可以是其他类型,也就是说,实践中你甚至可以将i32与struct进行比较,只要实现了对应的PartialEq;
Rust中的lhs和rhs指的是,“left-hand side”(左手边) 和 “right-hand side”(右手边)的参数。
3.2 对应操作符
这个比较简单,PartialEq和Eq一致,拥有的eq和ne方法分别对应==和!=两个操作符。Rust的大部分基本类型如整型、浮点数、字符串等都实现了PartialEq, 所以它们可以使用==和!=进行相等性比较。
3.3 可派生
英文描述为Derivable,即通过derive宏可以为自定义复合类型(struct/enum/union类型)自动实现PartialEq,用法如下:
#[derive(PartialEq)]
struct Book {name: String,
}#[derive(PartialEq)]
enum BookFormat { Paperback, Hardback, Ebook }#[derive(PartialEq)]
union T {a: u32,b: f32,c: f64,
}
需要注意的是,可派生的前提是这个复合类型下的所有成员字段都是支持PartialEq的,下面的代码说明了这种情况:
// #[derive(PartialEq)] // 取消注释即可编译通过
enum BookFormat { Paperback, Hardback, Ebook }// 无法编译!!!
#[derive(PartialEq)]
struct Book {name: String,format: BookFormat, // 未实现PartialEq
}
扩展:使用
cargo expand命令可以打印出宏为类型实现的PartialEq代码。
3.4 手动实现PartialEq
以上一段代码为例,我们假设BookFormat是引用其他crate下的代码,无法为其添加derive语句(不能修改它),此时就需要手动为Book手动实现PartialEq,代码如下:
enum BookFormat { Paperback, Hardback, Ebook }struct Book {name: String,format: BookFormat,
}// 要求只要name相等则Book相等(假设format无法进行相等比较)
impl PartialEq for Book {fn eq(&self, other: &Self) -> bool {self.name == other.name}
}fn main() {let bk = Book { name: "x".to_string(), format: BookFormat::Ebook };let bk2 = Book { name: "x".to_string(), format: BookFormat::Paperback };assert!(bk == bk2); // 因为Book实现了PartialEq,所以可以比较相等性
}
3.5 比较不同的类型
根据上面的trait定义中,我们知道了只要在实现PartialEq时关联不同类型的Rhs参数,就能比较不同类型的相等性。示例代码如下:
#[derive(PartialEq)]
enum WheelBrand {Bmw,Benz,Michelin,
}struct Car {brand: WheelBrand,price: i32,
}impl PartialEq<WheelBrand> for Car {fn eq(&self, other: &WheelBrand) -> bool {self.brand == *other}
}fn main() {let car = Car { brand: WheelBrand::Benz, price: 10000 };let wheel = WheelBrand::Benz;// 比较 struct和enumassert!(car == wheel);// assert!(wheel == car); // 无法反过来比较
}
需要注意的是,代码片段中仅实现了Car与Wheel的相等性比较,若要反过来比较,还得提供反向的实现,如下:
impl PartialEq<Car> for WheelBrand {fn eq(&self, other: &Car) -> bool {*self == other.brand}
}
3.6 Rust基本类型如何实现PartialEq
上文说过,Rust的基本类型都实现了PartialEq,那具体是怎么实现的呢?是为每个类型都写一套impl代码吗?代码在哪呢?
如果你使用IDE,可以通过在任意位置按住ctrl键(视IDE而定)点击代码中的PartialEq以打开其在标准库中的代码文件cmp.rs,相对路径是RUST_LIB_DIR/core/src/cmp.rs 。
在该文件中可以找到如下宏代码:
mod impls {// ...macro_rules! partial_eq_impl {($($t:ty)*) => ($(#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const PartialEq for $t {#[inline]fn eq(&self, other: &$t) -> bool { (*self) == (*other) }#[inline]fn ne(&self, other: &$t) -> bool { (*self) != (*other) }})*)}partial_eq_impl! {bool char usize u8 u16 u32 u64 u128 isize i8 i16 i32 i64 i128 f32 f64}// ...
}
这里使用了Rust强大的宏特性(此处使用的是声明宏,还算简单),来为Rust的众多基本类型快速实现了PartialEq trait。如果你还不了解宏,可以暂且理解其是一种编写重复模式代码规则的编程特性,它可以减少大量重复代码。
4. Eq
理解了PartialEq,那Eq理解起来就非常简单了,本节的内容主体与PartialEq基本一致,所以相对简明。
4.1 trait定义
如下:
pub trait Eq: PartialEq<Self> {fn assert_receiver_is_total_eq(&self) {}
}
根据代码可以得到两个重要信息:
- Eq是继承自PartialEq的;
- Eq相对PartialEq只多了一个方法
assert_receiver_is_total_eq(),并且有默认实现;
第一个,既然Eq继承自PartialEq,说明想要实现Eq,必先实现PartialEq。第二个是这个assert_receiver_is_total_eq()
方法了,简单来说,它是被derive语法内部使用的,用来断言类型的每个属性都实现了Eq特性,对于使用者的我们来说, 其实不用过多关注。
4.2 对应操作符
与PartialEq无差别,略。
4.3 可派生
与PartialEq的使用相似,只是要注意派生时,由于继承关系,Eq和PartialEq必须同时存在。
#[derive(PartialEq, Eq)] // 顺序无关
struct Book {name: String,
}
4.4 手动实现Eq
直接看代码:
enum BookFormat { Paperback, Hardback, Ebook }struct Book {name: String,format: BookFormat,
}// 要求只要name相等则Book相等(假设format无法进行相等比较)
impl PartialEq for Book {fn eq(&self, other: &Self) -> bool {self.name == other.name}
}impl Eq for Book {}fn main() {let bk = Book { name: "x".to_string(), format: BookFormat::Ebook };let bk2 = Book { name: "x".to_string(), format: BookFormat::Paperback };assert!(bk == bk2);
}
需要注意的是,必须先实现PartialEq,再实现Eq。另外,这里能看出的是,在比较相等性方面,Eq和PartialEq都是使用==和!=操作符,无差别感知。
4.5 比较不同的类型
与PartialEq无差别,略。
4.6 Rust基本类型如何实现Eq
与PartialEq一样,在相对路径为RUST_LIB_DIR/core/src/cmp.rs的文件中,存在如下宏代码:
mod impls {/*... (先实现PartialEq)*/// 再实现Eqmacro_rules! eq_impl {($($t:ty)*) => ($(#[stable(feature = "rust1", since = "1.0.0")]impl Eq for $t {})*)}eq_impl! { () bool char usize u8 u16 u32 u64 u128 isize i8 i16 i32 i64 i128 }
}
5. 对浮点数的测试
目前在标准库中,笔者只发现有浮点数是只实现了PartialEq的(以及包含浮点数的复合类型),下面是浮点数的测试代码:
fn main() {fn check_eq_impl<I: Eq>(typ: I) {}// check_eq_impl(0.1f32); // 编译错误// check_eq_impl(0.1f64); // 编译错误let nan = f32::NAN;let infinity = f32::INFINITY;let neg_infinity = f32::NEG_INFINITY;assert_ne!(nan, nan); // 不等!assert_eq!(infinity, infinity); // 相等!assert_eq!(neg_infinity, neg_infinity); // 相等!
}
6. PartialOrd和Ord
6.1 与PartialEq和Eq的关系
很多时候,当我们谈到PartialEq和Eq时,PartialOrd和Ord总是不能脱离的话题,因为它们都是一种二元比较关系,前两者是相等性比较,后两者是有序性(也可称大小性)比较。 前两者使用的操作符是==和!=
,后两者使用的操作符是>、=
、<,没错,PartialOrd和Ord的比较结果是包含等于的,然后我们可以基于这个有序关系来对数据进行排序(sort)。
重点:有序性包含相等性。
与PartialEq存在的原因一样,PartialOrd的存在的理由也是因为有一些类型是不具有有序性关系的(无法比较),比如浮点数、Bool、Option、函数、闭包等类型。
PartialEq和Eq、PartialOrd和Ord共同描述了Rust中任意类型的二元比较关系,包含相等性、有序性。 所以在上文中,你可能也观察到PartialOrd和Ord的定义也位于cmp.rs文件中。
我们可以将PartialOrd和Ord直译为偏序和全序关系,因为这确实是它们要表达的含义。偏序和全序的概念来自离散数学,下文详解。
6.2 基本性质
PartialOrd和Ord也是满足一定的基本性质的,PartialOrd满足:
- 传递性:若有
a<b、b<c,则a<c。且>和==也是一样的; - 对立性:若有
a<b,则b>a;
Ord基于PartialOrd,自然遵循传递性和对立性,另外对于任意两个元素,还满足如下性质:
- 确定性:必定存在
>或==或<其中的一个关系;
6.3 trait定义
1. PartialOrd trait
// 二元关系定义(<,==,>)
pub enum Ordering {Less = -1,Equal = 0,Greater = 1,
}pub trait PartialOrd<Rhs: ?Sized = Self>: PartialEq<Rhs> {fn partial_cmp(&self, other: &Rhs) -> Option<Ordering>;fn lt(&self, other: &Rhs) -> bool {matches!(self.partial_cmp(other), Some(Less))}fn le(&self, other: &Rhs) -> bool {matches!(self.partial_cmp(other), Some(Less | Equal))}fn gt(&self, other: &Rhs) -> bool {matches!(self.partial_cmp(other), Some(Greater))}fn ge(&self, other: &Rhs) -> bool {matches!(self.partial_cmp(other), Some(Greater | Equal))}
}
基本信息:
- PartialOrd继承自PartialEq,这很好理解,无法比较大小的类型也一定不能进行相等性比较;
- 提供
partial_cmp()方法用于主类型和可以是其他类型的参数比较,返回的Option<Ordering>,表示两者关系可以是无法比较的(None),那么这里我们就可以联想到Ord
trait返回的肯定是Ordering(因为具有全序的类型不会存在无法比较的情况); - 另外四个方法分别实现了对应的操作符:
<,<=,>,>=,即实现了PartialOrd的类型可以使用这些操作符进行比较;除此之外,由于继承了PartialEq,所以还允许使用==,!=;
请再次记住,不管是PartialOrd还是Ord,都包含相等关系。
2. Ord trait
pub trait Ord: Eq + PartialOrd<Self> {// 方法1fn cmp(&self, other: &Self) -> Ordering;// 方法2fn max(self, other: Self) -> SelfwhereSelf: Sized,Self: ~ const Destruct,{// HACK(fee1-dead): go back to using `self.max_by(other, Ord::cmp)`// when trait methods are allowed to be used when a const closure is// expected.match self.cmp(&other) {Ordering::Less | Ordering::Equal => other,Ordering::Greater => self,}}// 方法3fn min(self, other: Self) -> SelfwhereSelf: Sized,Self: ~ const Destruct,{// HACK(fee1-dead): go back to using `self.min_by(other, Ord::cmp)`// when trait methods are allowed to be used when a const closure is// expected.match self.cmp(&other) {Ordering::Less | Ordering::Equal => self,Ordering::Greater => other,}}// 方法4fn clamp(self, min: Self, max: Self) -> SelfwhereSelf: Sized,Self: ~ const Destruct,Self: ~ const PartialOrd,{assert!(min <= max);if self < min {min} else if self > max {max} else {self}}
}
基本信息:
cmp方法用于比较self与参数other的二元关系,返回Ordering类型(区别于PartialOrd.partial_cmp()返回的Option<Ordering>);- Ord继承自Eq+PartialOrd,这也很好理解,具有全序关系的类型自然具有偏序关系;
- 提供
min/max()方法以返回self与参数other之间的较小值/较大值; - 额外提供
clamp()方法返回输入的参数区间内的值; - 显然,由于继承了PartialOrd,所以实现了Ord的类型可以使用操作符
<,<=,>,>=,==,!=;
对
Self: ~ const Destruct的解释:位于where后即是类型约束,这里约束了Self类型必须是实现了Destructtrait的一个指向常量的裸指针。
全序和偏序的概念(来自离散数学)
- 全序:即全序关系,自然也是一种二元关系。全序是指,集合中的任两个元素之间都可以比较的关系。比如实数中的任两个数都可以比较大小,那么“大小”就是实数集的一个全序关系。
- 偏序:集合中只有部分元素之间可以比较的关系。比如复数集中并不是所有的数都可以比较大小,那么“大小”就是复数集的一个偏序关系。
- 显然,全序关系必是偏序关系。反之不成立。
6.4 可派生
1. PartialOrd derive
PartialOrd和Ord也是可以使用derive宏进行自动实现的,代码如下:
#[derive(PartialOrd, PartialEq)]
struct Book {name: String,
}#[derive(PartialOrd, PartialEq)]
enum BookFormat { Paperback, Hardback, Ebook }
这里有几点需要注意:
- 由于继承关系,所以必须同时派生PartialEq;
- 与PartialEq相比,不支持为
union类型派生; - 对struct进行派生时,大小顺序依据的是成员字段的字典序(字母表中的顺序,数字与字母比较则根据ASCII表编码,数字编码<字母编码;若比较多字节字符如中文,则转Unicode编码后再比较;
实际上ASCII表中的字符编码与对应Unicode编码一致); - 对enum进行派生时,大小顺序依据的是枚举类型的值大小,默认情况下,第一个枚举类型的值是1,向下递增1,所以第一个枚举最小;
下面使用代码对第2,3点举例说明:
#[derive(PartialOrd, PartialEq)]
struct Book {name: String,
}
assert!(Book { name: "a".to_string() } < Book { name: "b".to_string() });
assert!(Book { name: "b".to_string() } < Book { name: "c".to_string() });
// 字典序中,数字<字母(按ASCII编码排序)
assert!(Book { name: "1".to_string() } < Book { name: "2".to_string() });
assert!(Book { name: "2".to_string() } < Book { name: "a".to_string() });
// 字典序中,如果比较多字节字符,则先转为其Unicode的十六进制形式,然后逐字节比较
// 比如 中文 "曜" 和 "耀" 的Unicode编码分别为0x66DC和0x8000,所以前者小于后者
assert_eq!("曜", "\u{66dc}");
assert_eq!("耀", "\u{8000}");
assert!(Book { name: "曜".to_string() } < Book { name: "耀".to_string() });#[derive(PartialOrd, PartialEq)]
enum BookFormat {Paperback,// 1Hardback,// 2Ebook, // 3
}
assert!(BookFormat::Paperback < BookFormat::Hardback);
assert!(BookFormat::Hardback < BookFormat::Ebook);#[derive(PartialOrd, PartialEq)]
enum BookFormat2 {// 手动指定枚举的值,则可以改变它们的大小顺序Paperback = 3,Hardback = 2,Ebook = 1,
}
assert!(BookFormat2::Paperback > BookFormat2::Hardback);
assert!(BookFormat2::Hardback > BookFormat2::Ebook);
对于字典序比较规则,还有一些特殊情况,如下:
- 如果元素A是元素B的前缀,则元素A<元素B;
- 空字符序列<非空字序列;
2. Ord derive
#[derive(Ord, Eq, PartialOrd, PartialEq)]
struct Book {name: String,
}#[derive(Ord, Eq, PartialOrd, PartialEq)]
enum BookFormat {Paperback,Hardback,Ebook,
}
这里只需注意一点,那就是由于继承关系,Ord需要和Eq, PartialOrd, PartialEq同时派生。另外,根据前面所提到的,PartialOrd和Ord都支持>=, <=,这个要记得;
6.5 手动实现PartialOrd和Ord
1. PartialOrd Impl
// 注意这里测试对象是Book3,不要为成员字段format即BookFormat3派生任何trait,模拟实际项目中无法修改成员字段特性的情况
enum BookFormat3 {Paperback,Hardback,Ebook,
}struct Book3 {name: String,format: BookFormat3,
}// -- 先得实现 PartialEq
impl PartialEq<Self> for Book3 {// tips:这里可以将<Self>省略fn eq(&self, other: &Self) -> bool {self.name == other.name// 这里假设format字段不要求比较}
}// -- 才能实现 PartialOrd
impl PartialOrd for Book3 {fn partial_cmp(&self, other: &Self) -> Option<Ordering> {// 直接调用name(String)的比较方法,如果成员字段也没有实现PartialOrd,那就得先为成员实现,这类情况很少self.name.partial_cmp(&other.name)}
}
2. Ord Impl
// 测试对象:Book3
// - 这里同样没有使用任何derive,全手动实现,由于继承关系,需要实现四个trait
// - 注意:若存在任一成员字段(这里指 format字段)未实现PartialEq/Eq/PartialOrd,都是无法为Book3派生Ord的(派生时不会解析下面的手动impl)
enum BookFormat3 {Paperback,Hardback,Ebook,
}struct Book3 {name: String,format: BookFormat3,
}// -- 先实现 PartialEq
impl PartialEq for Book3 {fn eq(&self, other: &Book3) -> bool {self.name == other.name// 这里假设format字段不要求比较}
}// -- 再实现 Eq
impl Eq for Book3 {}// -- 再实现 Ord
impl Ord for Book3 {fn cmp(&self, other: &Book3) -> Ordering {// 直接调用name(String)的cmp方法(当需要实现Ord时,成员字段一般都实现了Ord,可直接调用其cmp方法)self.name.cmp(&other.name)}
}// -- 最后实现 PartialOrd
impl PartialOrd for Book3 {fn partial_cmp(&self, other: &Book3) -> Option<Ordering> {// 直接调用上面实现的cmp方法Some(self.cmp(&other))}
}
阅读此代码需要注意几点:
- 先读完代码注释;
- 请注意是先实现Ord,再实现PartialOrd,理由是既然一开始就想要为类型实现Ord,说明类型是能够得出一个肯定结果的(非None),所以后实现PartialOrd直接调用Ord的
cmp();
6.6 比较不同的类型
这一节不贴代码了,留给读者去实现。具体实现手法可参考前面3.5节或4.5节中的内容。
6.7 Rust基本类型如何实现PartialOrd和Ord
1. PartialOrd impl macro
我们以前面介绍过的同样的方式找到cmp.rs中PartialOrd的实现宏,代码如下:
mod impls {// ... 前面是PartialEq和Eq的宏实现macro_rules! partial_ord_impl {($($t:ty)*) => ($(#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const PartialOrd for $t {#[inline]fn partial_cmp(&self, other: &$t) -> Option<Ordering> {// 注意看,此处是根据两个比较结果来得到最终结果,本质上是要求比较的值满足对立性(浮点数NaN不满足,所以返回None)match (*self <= *other, *self >= *other) {(false, false) => None,(false, true) => Some(Greater),(true, false) => Some(Less),(true, true) => Some(Equal),}}#[inline]fn lt(&self, other: &$t) -> bool { (*self) < (*other) }#[inline]fn le(&self, other: &$t) -> bool { (*self) <= (*other) }#[inline]fn ge(&self, other: &$t) -> bool { (*self) >= (*other) }#[inline]fn gt(&self, other: &$t) -> bool { (*self) > (*other) }})*)}#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const PartialOrd for () {#[inline]fn partial_cmp(&self, _: &()) -> Option<Ordering> {Some(Equal)}}#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const PartialOrd for bool {#[inline]fn partial_cmp(&self, other: &bool) -> Option<Ordering> {Some(self.cmp(other))}}partial_ord_impl! { f32 f64 }
}
这里要注意一下几点:
- 代码中定义的宏
partial_ord_impl!是通过两个比较结果来得到最终结果(看注释); - 这个宏除了应用在了浮点数类型上,还应用在了
()和bool类型。浮点数类型不必多说,单元类型是一种单值类型用于排序的情况也比较少,为bool类型实现这个trait的原因是:
有时我们需要对包含bool类型成员的struct或enum进行排序,所以需要为其实现PartialOrd(注意其实现也是调用self.cmp());
这里的
impl const中的const关键字意味着标记这个trait实现是编译时常量(编译时优化),以保证运行时不会有额外开销。这里是因为fn partial_cmp()的实现没有修改任何数据才可以加const,当然还有其他要求例如不能使用动态分配的内存(例如 Box 或 Vec)、不能调用非 const 函数等;
2. Ord impl macro
mod impls {// ... 前面是PartialEq/Eq/PartialOrd的宏实现macro_rules! ord_impl {($($t:ty)*) => ($(#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const PartialOrd for $t {#[inline]fn partial_cmp(&self, other: &$t) -> Option<Ordering> {Some(self.cmp(other))}#[inline]fn lt(&self, other: &$t) -> bool { (*self) < (*other) }#[inline]fn le(&self, other: &$t) -> bool { (*self) <= (*other) }#[inline]fn ge(&self, other: &$t) -> bool { (*self) >= (*other) }#[inline]fn gt(&self, other: &$t) -> bool { (*self) > (*other) }}#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const Ord for $t {#[inline]fn cmp(&self, other: &$t) -> Ordering {// The order here is important to generate more optimal assembly.// See <https://github.com/rust-lang/rust/issues/63758> for more info.if *self < *other { Less }else if *self == *other { Equal }else { Greater }}})*)}#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const Ord for () {#[inline]fn cmp(&self, _other: &()) -> Ordering {Equal}}#[stable(feature = "rust1", since = "1.0.0")]#[rustc_const_unstable(feature = "const_cmp", issue = "92391")]impl const Ord for bool {#[inline]fn cmp(&self, other: &bool) -> Ordering {// Casting to i8's and converting the difference to an Ordering generates// more optimal assembly.// See <https://github.com/rust-lang/rust/issues/66780> for more info.match (*self as i8) - (*other as i8) {-1 => Less,0 => Equal,1 => Greater,// SAFETY: bool as i8 returns 0 or 1, so the difference can't be anything else_ => unsafe { unreachable_unchecked() },}}}ord_impl! { char usize u8 u16 u32 u64 u128 isize i8 i16 i32 i64 i128 }
}
这里需要了解一下几点:
- 实现Ord的时候需要同时实现PartialOrd,不要求实现的顺序。PartialOrd的
partial_cmp()内部调用的是Ord的cmp(),理由前面讲过; - 同样为
()和bool类型实现了Ord; - 为大部分基本类型
char usize u8 u16 ...实现了Ord;
6.8 为其他类型实现四大compare-trait
这里指的其他类型是!、不可变借用类型、可变借用类型,具体实现代码就在源码中刚刚看的宏ord_impl!下方,此处就不再赘述。
相关文章:

【Rust】一文讲透Rust中的PartialEq和Eq
前言 本文将围绕对象:PartialEq和Eq,以及PartialOrd和Ord,即四个Rust中重点的Compare Trait进行讨论并解释其中的细节,内容涵盖理论以及代码实现。 在正式介绍PartialEq和Eq、以及PartialOrd和Ord之前,本文会首先介绍…...

Vulnhub靶场----9、DC-9
文章目录一、环境搭建二、渗透流程三、思路总结一、环境搭建 DC-9下载地址:https://download.vulnhub.com/dc/DC-9.zip kali:192.168.144.148 DC-9:192.168.144.158 二、渗透流程 1、信息收集nmap -T5 -A -p- -sV -sT 192.168.144.158思路&am…...
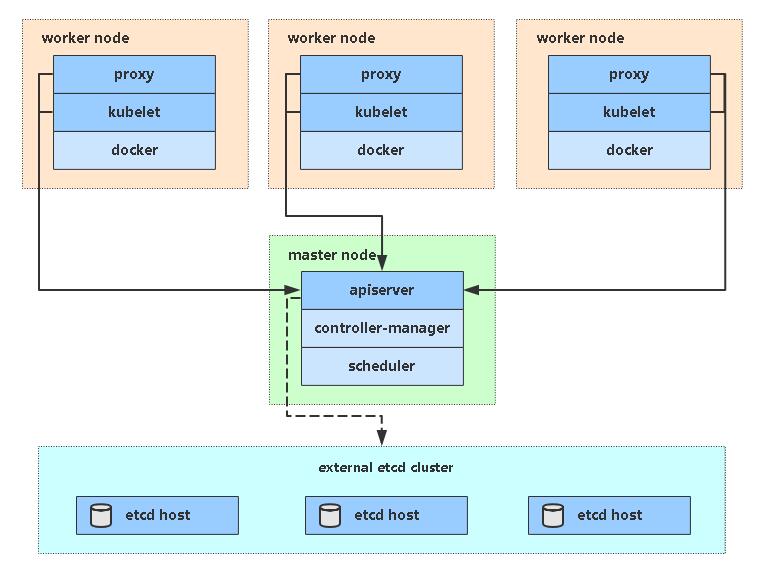
使用Containerd搭建K8s集群【v1.25】
[toc] 一、安装要求 在开始之前,部署Kubernetes集群机器需要满足以下几个条件: 一台或多台机器,操作系统 CentOS7.x-86_x64硬件配置:2GB或更多RAM,2个CPU或更多CPU,硬盘30GB或更多集群中所有机器之间网络互通可以访问外网,需要拉取镜像禁止swap分区二、准备环境 角色IP…...
)
NMT - 构建双语概率词典(Probabilistic dictionaries)
文章目录一、安装依赖包mosesdecoder安装 mgiza二、数据预处理三、训练本文参考:How to train your Bicleaner https://github.com/bitextor/bicleaner/wiki/How-to-train-your-Bicleaner 一、安装依赖包 这个过程主要依赖于 mosesdecodermgiza mosesdecoder git…...
《ChatGPT是怎样炼成的》
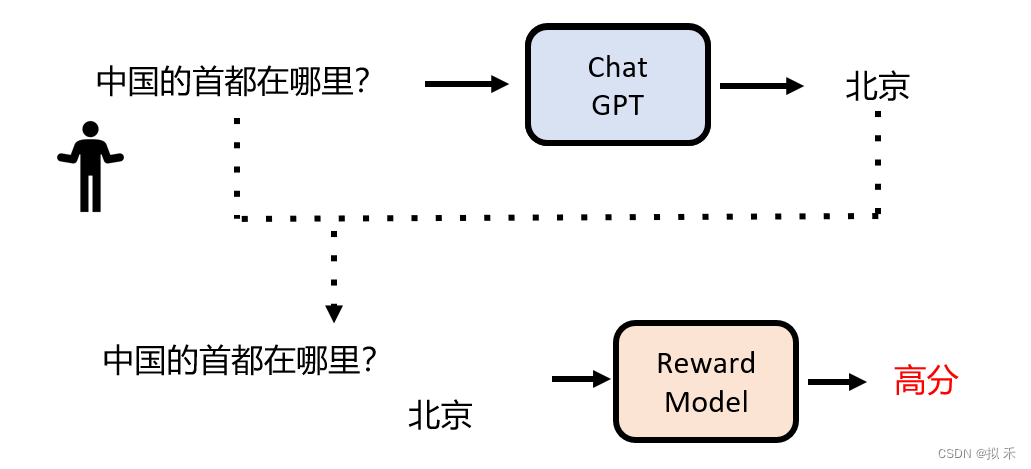
ChatGPT 在全世界范围内风靡一时,我现在每天都会使用 ChatGPT 帮我回答几个问题,甚至有的时候在一天内我和它对话的时间比和正常人类对话还要多,因为它确实“法力无边,功能强大”。 ChatGPT 可以帮助我解读程序,做翻译…...
Streaming System是第一章翻译
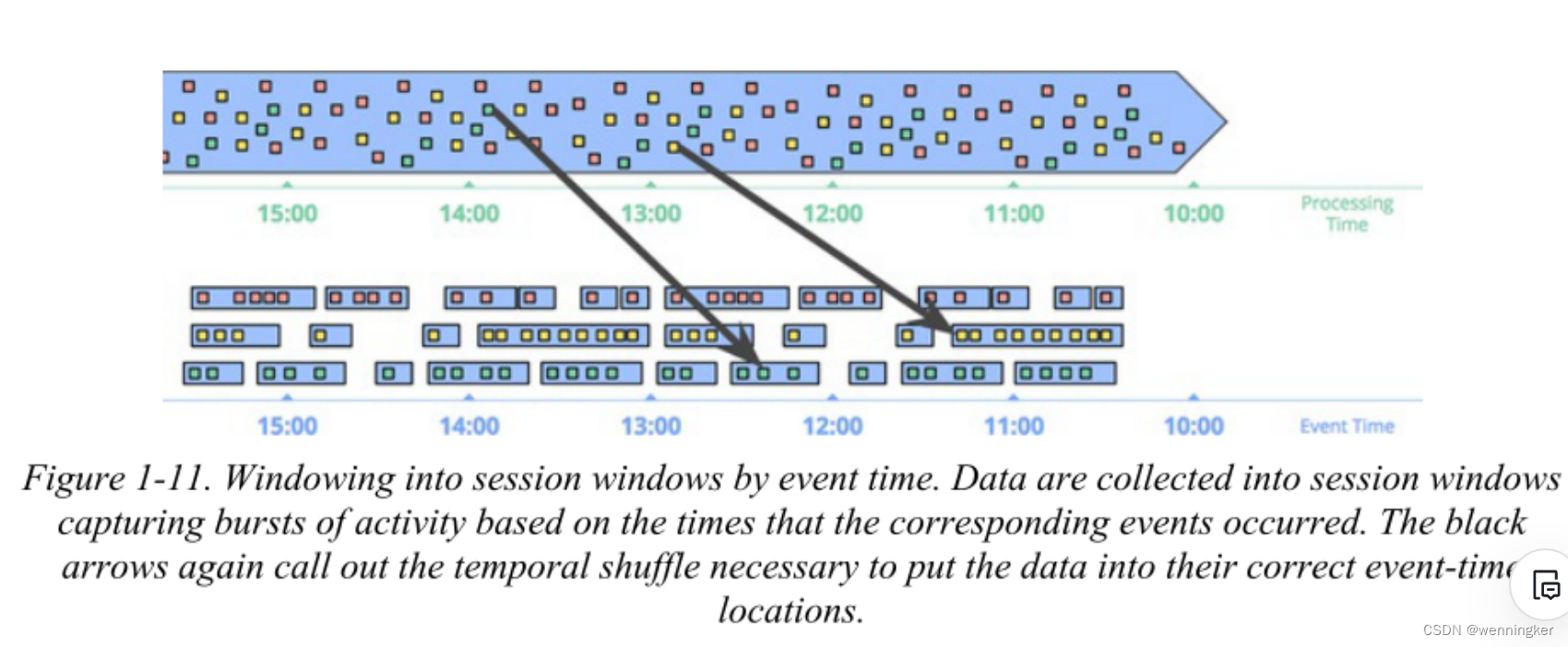
GIthub链接,欢迎志同道合的小伙伴一起翻译 Chapter 1.Streaming101 如今,流数据处理在大数据中是非常重要的,其主要原因是: 企业渴望对他们的数据有更及时的了解,而转换到流处理是实现更低延迟的一个好方法…...
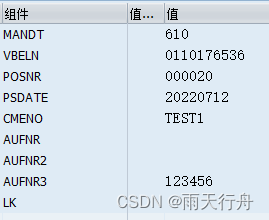
abap MODIFY常用语法解析
MODIFY 是既可以操作数据又可以操作内表的一个语法, 实现的逻辑都一样. 如果你内表或数据库中存在该行数据会对该行数据进行更新. 如果不存在,就会插入数据. , 1.如果it_tab是带有标题行的内表,是可以忽略FROM wa_tab工作区的 MODIFY it_tab .2.把工作区wa_tab中的数据更新…...

[媒体分流直播]媒体直播和传统直播的区别,以及媒体直播的特点
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 直播毋庸置疑已经融入到了我们生活的方方面面,小到才艺,游戏,大到政策的发布,许多企业和机构也越来越重视直播,那么一场活动怎…...
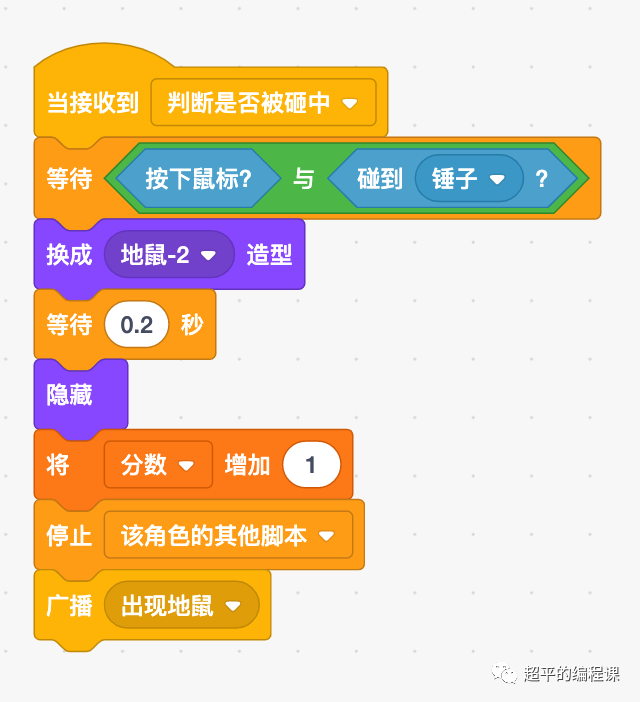
打地鼠游戏-第14届蓝桥杯STEMA测评Scratch真题精选
[导读]:超平老师的《Scratch蓝桥杯真题解析100讲》已经全部完成,后续会不定期解读蓝桥杯真题,这是Scratch蓝桥杯真题解析第102讲。 蓝桥杯选拔赛现已更名为STEMA,即STEM 能力测试,是蓝桥杯大赛组委会与美国普林斯顿多…...
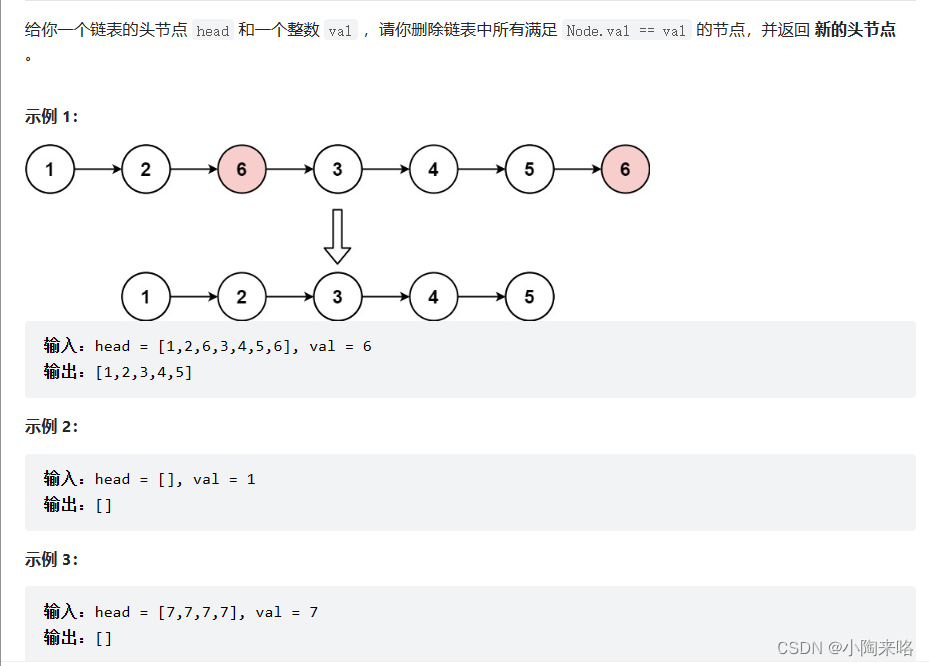
链表经典刷题--快慢指针与双指针
本篇总结链表解题思路----快慢指针,其实也就是双指针,这个快慢并不单纯指“快慢”,它更多的可以表示,速度快慢,距离长度,时间大小等等,用法很有趣也很独特,理解它的思想,…...

【Java集合框架】篇四:Set接口
1. Set及主要实现类特点 Set:无序、不可重复(去重)、存储value HashSet:底层使用HashMap,即使用 数组单项链表红黑树 结构进行存储。(jkd8中) LinkedHashSet:是HashSet的子类&…...

Python 数据库连接 + 创建库表+ 插入【内含代码实例】
人生苦短 我用python Python其他实用资料:点击此处跳转文末名片获取 数据库连接 连接数据库前,请先确认以下事项: 您已经创建了数据库 TESTDB.在TESTDB数据库中您已经创建了表 EMPLOYEEEMPLOYEE表字段为 FIRST_NAME, LAST_NAME, AGE, SEX 和 INCOME。连…...
DSS 部署环境需求清单
文章目录 DSS系统需求项目地址计算资源计算基准:计算引擎程序硬件需求表 :DSS计算及存储资源需求计算资源计算基准:计算程序硬件需求表:DSS系统需求 项目地址 https://github.com/WeBankFinTech/DataSphereStudio 计算资源计算基准: 1.日活用户10万。 2.单用户单日总…...

Python的面向对象,详细讲解Python之用处等基本常识
目录 Python 面向对象 面向对象技术简介 创建类 实例 实例 self代表类的实例,而非类 实例 创建实例对象 访问属性 实例 Python内置类属性 实例 python对象销毁(垃圾回收) 实例 实例 类的继承 实例 方法重写 实例 基础重载方法 运算符重载 实例…...
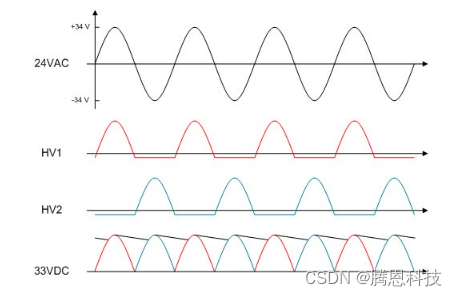
如何使用固态继电器为恒温器供电
恒温器有两种电源:电池和 24VAC。恒温器需要电池才能不间断地运行。电池消耗的能量尽可能低非常重要,但即使您最大限度地减少消耗,这仍然不是一个用户友好的选择,因为电池会不时需要更换。要降低更换频率,可以使用 24V…...
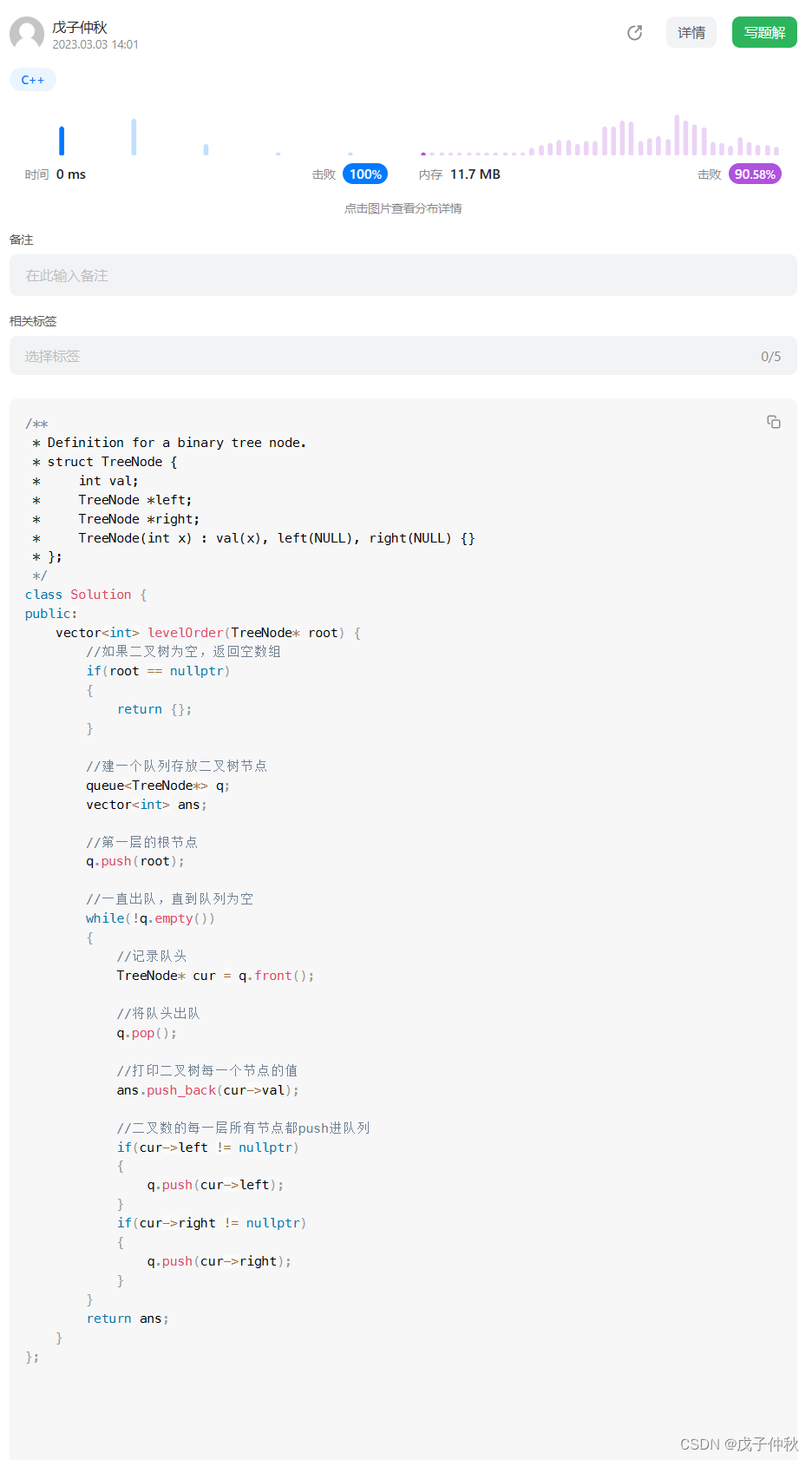
【LeetCode】剑指 Offer(14)
目录 题目:剑指 Offer 32 - I. 从上到下打印二叉树 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 32…...
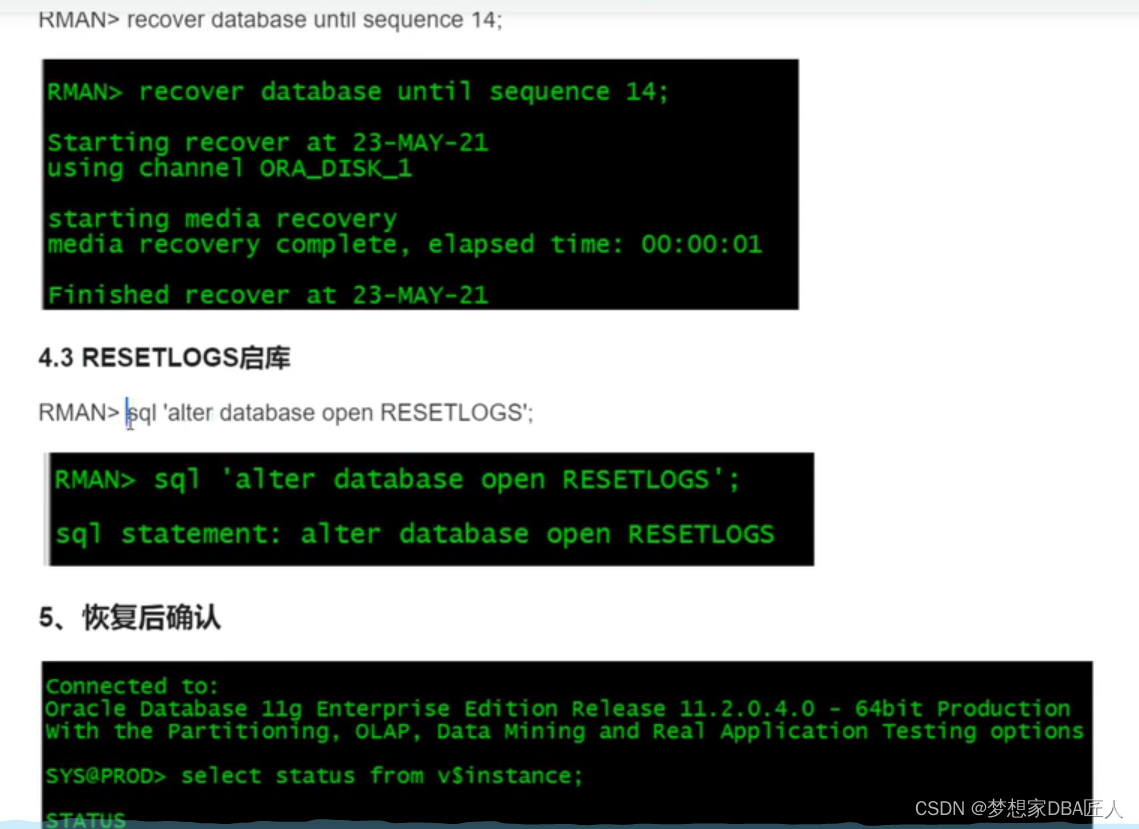
Rman单实例迁移到单实例
关于同平台同版本数据库之间的迁移操作的实验 ---Source DB[rootoracle-db-19cs ~]# cat /etc/redhat-release CentOS Stream release 8 [rootoracle-db-19cs ~]# --- Target DB[rootoracle-db-19ct ~]# cat /etc/redhat-release CentOS Stream release 8 [rootoracle-db-19ct…...

毕业设计 基于stm32舞台彩灯控制器设计app控制系统
基于stm32舞台彩灯控制器设计app控制1、项目简介1.1 系统构成1.2 系统功能2、部分电路设计2.1 STM32F103C8T6核心系统电路设计2.2 WS2812RGB彩灯电路设计3、部分代码展示3.1 控制WS2812显示颜色3.2 设置RGB灯的颜色,角度,亮度实物图1、项目简介 选题指导…...
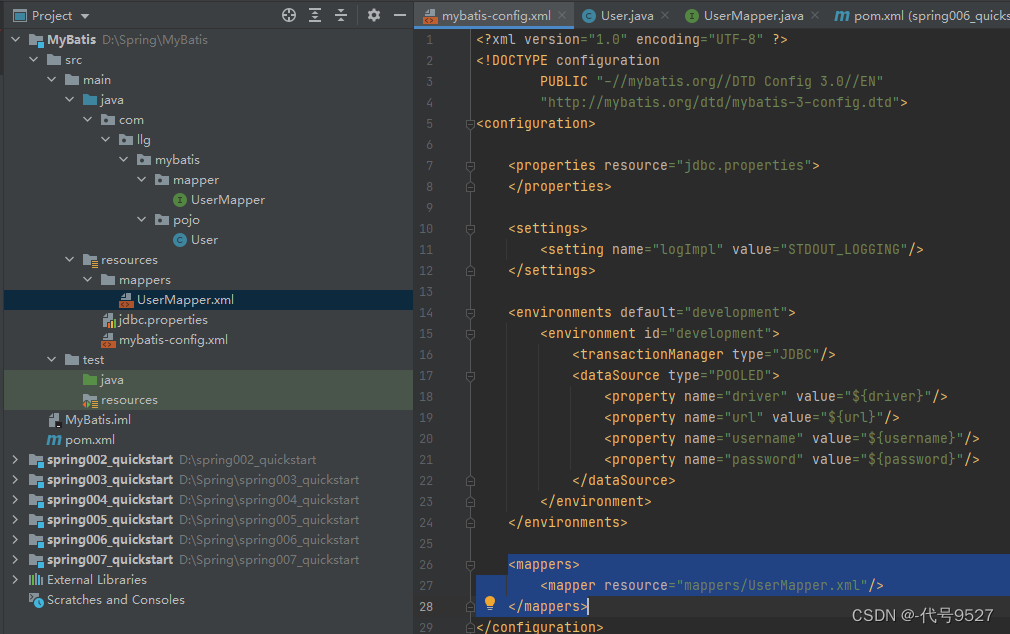
【MyBatis】篇一.
文章目录1、MyBatis概述2、环境搭建1、MyBatis概述 认识: JavaEE开发的一个套件SSM,即: MyBatis是一个持久层的框架,是对JDBC的一个封装,是一个半自动的ORM框架。 ORM即实体类对象和数据库中的数据的一个映射关系&am…...

【JavaScript速成之路】JavaScript流程控制
📃个人主页:「小杨」的csdn博客 🔥系列专栏:【JavaScript速成之路】 🐳希望大家多多支持🥰一起进步呀! 文章目录前言1,流程控制2,分支结构2.1,if语句2.2&…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
