软性演员-评论家算法 SAC
软性演员-评论家算法 SAC
- 软性演员-评论家算法 SAC
- 优势原理
- 软性选择
- 模型结构
- 目标函数
- 重参数化
- 熵正则化
- 代码实现
软性演员-评论家算法 SAC
优势原理
DDPG 的问题在于,训练不稳定、收敛差、依赖超参数、不适应复杂环境。
软性演员-评论家算法 SAC,更稳定,更适应复杂环境。
传统强化学习策略,采用 ε-greedy 贪心策略。
-
过度利用已知最优策略,老是在同一个地方用同一个策略
-
忽视对未知状态和未知最优动作的探索,容易忽视复杂环境的动态变化
-
DDPG 每个时刻只给了一个最优策略,这个最优策略很大程度还是之前的经验
软性在这里的意思是,软性选择,用于平滑探索和利用的关系。
比如走迷宫,你有很多选择:向前走、向后走、转向等。
- 在没有 SAC 的情况下,如果你发现一条看似可行的路线(已知最佳经验和动作),你可能会一直沿着这条路线走,即使它可能不是最佳路径。
- 有了 SAC,就好比你不仅想尽快找到出路,还想探索迷宫中的每个角落。即使某些路线看起来当前并不是最直接的出路,你也会尝试它们,因为你被鼓励去探索。
- 当 SAC 算法发现自己在某一区域过于确定或重复同样的路径时,它会因为想要增加熵(探索不确定性)而尝试新的动作,比如尝试之前没有走过的道路。
- 随着时间的推移,SAC 不仅找到了出路,而且可能发现了多条路径,因为它在探索过程中学到了迷宫的更多信息。
SAC 算法通过鼓励探索(即不总是走看起来最优的路径)来找到多个好的解决方案,并且它比其他算法更不容易陷入局部最优解,因为它总是在寻找新的可能性。
核心优势是,避免过早陷入局部最优解,至少也要找一个更大的局部最优解。
SAC 软性选择是基于熵,熵的作用是为了衡量不确性程度。
这意味着在评估一个动作的价值时,不仅考虑了奖励,还考虑了执行该动作后策略的熵。
目标不仅是最大化奖励,还要最大化熵,这意味着算法被鼓励探索更多不同的动作,即使它们不是当前看起来最优的。
最大熵强化学习不仅仅关注立即的奖励最大化,还关注保持策略的多样性和随机性,以促进更全面的探索。

这张图描绘的是软性演员-评论家算法(Soft Actor-Critic, SAC)中用到的一个关键概念,即多模态Q函数。
在这个图中,我们可以看到两个子图,3a和3b,它们展示了策略(π)和Q函数之间的关系。
图3a:
- π(at|st):这表示在给定状态st时,动作at的概率分布,这里假设为正态分布N(μ(st), Σ),其中μ(st)是均值函数,Σ是协方差矩阵。
- Q(st, at):这是Q函数在特定状态st和动作at下的值。Q函数衡量采取某动作并遵循当前策略预期可以获得的累积回报。
图3b:
- π(at|st) ∝ exp(Q(st, at)):这里显示了SAC中采用的最大熵策略,其中策略(即概率分布)与exp(Q(st, at))成正比。这意味着采取某个动作的概率不仅与预期回报(Q值)相关,还与该动作的熵有关。熵较高的动作即使预期回报不是最大,也可能被选中,这样鼓励了探索。
- Q(st, at):同样表示Q函数的值,但在这里,它与策略结合来形成一个调整后的策略分布。
这两个子图展示了如何从Q函数构建一个随机策略,这个策略不仅考虑最大化回报,还鼓励策略的多样性(探索)。在图3a中,我们只看到了策略的原始形态,而在图3b中,我们看到了这个策略如何通过与Q函数结合来调整,以包含探索性。
在SAC算法中,这种通过最大化熵来鼓励探索的策略非常重要,有助于避免局部最优解并找到更鲁棒的长期解决方案。
通过这种方式,SAC能够在学习过程中平衡探索和利用,提高智能体在复杂环境中的表现。
软性选择
在某些环境中,可能存在多种不同的策略都能获得高回报,这导致 动作价值 Q 函数 变得多模态(即有多个高值峰)。
传统的强化学习算法可能只能收敛到其中一个模态,也就是一个局部最优解,而忽略了其他可能同样好或者更好的策略。
为了解决这个问题,可以使用一种称为基于能量的策略来让策略更好地适应Q函数的多模态特性。
基于能量的策略通常采用玻尔兹曼分布的形式,这是一个概率分布,它根据能量函数给出了各个状态的概率。
玻尔兹曼分布(x轴是能量大小):
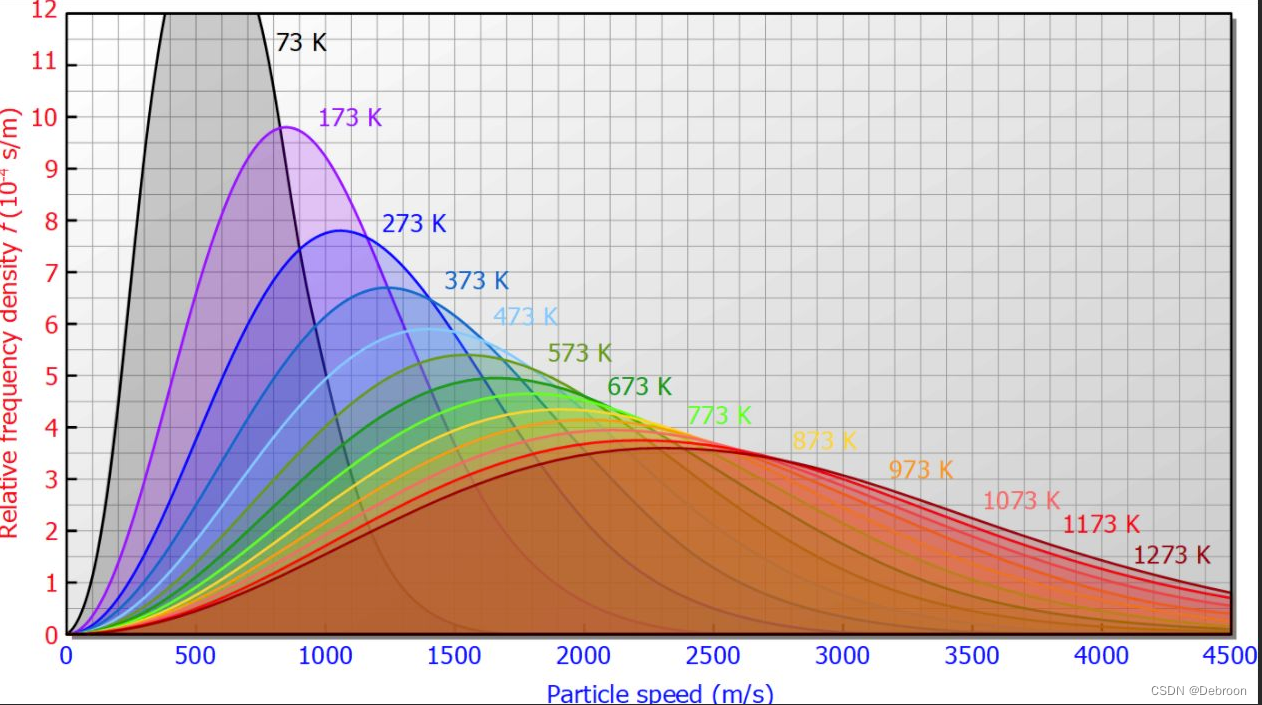
让策略收敛到 Q 函数 的玻尔兹曼分布形式,这个形式的分布就可以拟合上图的多个解。
玻尔兹曼分布可以用来选择动作,其中动作的选择概率与其Q值的指数成正比,公式如下:
- [ π ( a ∣ s ) = exp ( Q ( s , a ) / τ ) ∑ b exp ( Q ( s , b ) / τ ) ] [ \pi(a|s) = \frac{\exp(Q(s,a)/\tau)}{\sum_{b}\exp(Q(s,b)/\tau)} ] [π(a∣s)=∑bexp(Q(s,b)/τ)exp(Q(s,a)/τ)]
这里的 τ \tau τ 称为温度参数,它控制了策略的探索程度。
-
当 τ \tau τ 较大时,策略倾向于探索
-
当 τ \tau τ 较小时,策略倾向于利用
这种基于玻尔兹曼分布的策略平衡了探索和利用,有助于智能体在复杂环境中找到长期有效的解决方案。
理论上,当智能体的学习收敛时,它的策略会反映出Q函数的结构,优先选择预期回报高的动作,同时保持对其他可能性的探索,这样做可以避免局部最优解,并适应环境的变化。
模型结构

V网络(Value Network)
- 输入嵌入层(Input Embedder):对输入的观察数据进行预处理。
- 中间件(Middleware):通常是一系列的全连接层或其他类型的网络层,用于提取特征。
- 输出层(Dense):输出状态值(State Value),它代表了在给定状态下,遵循当前策略所能获得的预期回报。
策略网络(Policy Network)
- 输入嵌入层(Input Embedder):与V网络相同,对输入进行预处理。
- 中间件(Middleware):提取特征。
- 策略均值输出层(Dense, Policy Mean):预测给定状态下每个动作的均值。
- 策略标准差输出层(Dense, Log Policy Std):预测动作的对数标准差,通常会通过指数函数(Exponentiate)进行处理以确保标准差是正的。
- SAC头(SAC Head):结合均值和标准差定义了一个高斯分布,并从中采样动作(Sampled Actions)作为策略输出。
Q网络(Q Networks)
- 输入嵌入层(Input Embedder):分别对状态和动作进行预处理。
- 中间件(Middleware):提取特征。
- 输出层(Dense):存在两个Q网络,每个都输出一个状态-动作对的价值(State Action Value 1 & 2),这是为了减少估计偏差并提高稳定性。
这种结构允许SAC在做出决策时考虑到策略的多样性,并通过两个Q网络来减少值函数的过估计。
整个架构的目的是训练一个智能体,使其能在复杂环境中作出决策,同时通过熵正则化来鼓励探索未知的行为。
目标函数
Q网络更新损失函数:
L Q ( ϕ ) = E ( s i , q i , r i , s i + 1 ) ∼ D , a i + 1 ∼ π θ ( ⋅ ∣ s i + 1 ) [ 1 2 ( Q ϕ ( s i , a i ) − ( r i + γ ( min j = 1 , 2 Q ϕ ˙ j ( s t + 1 , a t + 1 ) − α log π ( a t + 1 ∣ s t + 1 ) ⏞ Entropy Iterm ) 2 ] L_Q(\phi)=\mathbb{E}_{(s_i,q_i,r_i,s_{i+1})\sim\mathcal{D},a_{i+1}\sim\pi_{\theta}(\cdot|s_{i+1})}\left[\frac{1}{2}\left(Q_{\phi}(s_i,a_i)-(r_i+\gamma(\min_{j=1,2}Q_{\dot{\phi}_j}(s_{t+1},a_{t+1})\overbrace{-\alpha\log\pi(a_{t+1}|s_{t+1})}^{\textbf{Entropy Iterm}} \right ) ^ 2 \right ] LQ(ϕ)=E(si,qi,ri,si+1)∼D,ai+1∼πθ(⋅∣si+1) 21 Qϕ(si,ai)−(ri+γ(minj=1,2Qϕ˙j(st+1,at+1)−αlogπ(at+1∣st+1) Entropy Iterm 2
- L Q ( ϕ ) L_Q(\phi) LQ(ϕ): 这是Q函数的损失函数,用来训练Q网络的参数 ϕ \phi ϕ。
- E ( s i , a i , r i , s i + 1 ) ∼ D \mathbb{E}_{(s_i, a_i, r_i, s_{i+1}) \sim \mathcal{D}} E(si,ai,ri,si+1)∼D: 这个期望表示对经验回放缓冲区 D \mathcal{D} D中的样本进行平均,包括状态 s i s_i si、动作 a i a_i ai、奖励 r i r_i ri和下一个状态 s i + 1 s_{i+1} si+1。
- a i + 1 ∼ π θ ( ⋅ ∣ s i + 1 ) a_{i+1} \sim \pi_{\theta}(\cdot|s_{i+1}) ai+1∼πθ(⋅∣si+1): 表示根据当前策略 π θ \pi_{\theta} πθ选择下一个动作 a i + 1 a_{i+1} ai+1。
- Q ϕ ( s i , a i ) Q_{\phi}(s_i, a_i) Qϕ(si,ai): Q网络使用参数 ϕ \phi ϕ来估计在状态 s i s_i si下采取动作 a i a_i ai的价值。
- r i + γ ( min j = 1 , 2 Q ϕ ˙ j ( s i + 1 , a i + 1 ) − α log π ( a i + 1 ∣ s i + 1 ) ) r_i + \gamma (\min_{j=1,2}Q_{\dot{\phi}_j}(s_{i+1}, a_{i+1}) - \alpha \log \pi(a_{i+1}|s_{i+1})) ri+γ(minj=1,2Qϕ˙j(si+1,ai+1)−αlogπ(ai+1∣si+1)): 这部分计算目标Q值,包括立即奖励 r i r_i ri加上对下一个状态-动作对的Q值的折现(考虑两个Q网络中较小的那个),再减去与策略熵相关的项,其中 γ \gamma γ是折现因子, α \alpha α是熵正则化的权重。
- α log π ( a i + 1 ∣ s i + 1 ) \alpha \log \pi(a_{i+1}|s_{i+1}) αlogπ(ai+1∣si+1): 这是熵正则化项, α \alpha α表示其权重。熵项鼓励策略进行探索,防止过早收敛到局部最优策略。
公式的原意:
- Q函数部分:不仅基于当前能得到多少分数来建议你的动作,而且还会考虑到未来可能得到的分数
- 最大熵部分:让游戏更有趣、多样性(探索),这种考虑未来的方式称为折现,意味着未来的分数在今天看来不那么值钱。
策略网络更新损失函数:
L π ( θ ) = E s t ∼ D , a t ∼ π θ [ α log ( π θ ( a t ∣ s t ) ) − Q ϕ ( s t , a t ) ] L_{\pi}(\theta)=\mathbb{E}_{s_{t}\sim\mathcal{D},a_{t}\sim\pi_{\theta}}[\alpha\log(\pi_{\theta}(a_{t}|s_{t}))-Q_{\phi}(s_{t},a_{t})] Lπ(θ)=Est∼D,at∼πθ[αlog(πθ(at∣st))−Qϕ(st,at)]
- L π ( θ ) L_{\pi}(\theta) Lπ(θ): 这是策略网络的损失函数,用于更新策略网络的参数 θ \theta θ。
- E s t ∼ D , a t ∼ π θ \mathbb{E}_{s_t \sim \mathcal{D}, a_t \sim \pi_{\theta}} Est∼D,at∼πθ: 这表示对经验回放缓冲区 D \mathcal{D} D中的状态s_t以及根据当前策略 π θ \pi_{\theta} πθ采取的动作 a t a_t at进行平均。
- α log ( π θ ( a t ∣ s t ) ) \alpha \log(\pi_{\theta}(a_t|s_t)) αlog(πθ(at∣st)): 这是策略熵的加权值, α \alpha α是熵的权重系数。这个熵项鼓励策略多样性,即鼓励策略产生更随机的动作。
- Q ϕ ( s t , a t ) Q_{\phi}(s_t, a_t) Qϕ(st,at): 这是Q网络评估在状态s_t下采取动作 a t a_t at的价值。
上面提到的两个公式共同工作以优化智能体的行为,但各自负责不同的部分:
-
Q函数的损失函数 L Q ( ϕ ) L_Q(\phi) LQ(ϕ):
- 负责更新Q网络,即学习评估在给定状态和动作下预期回报的函数。
- 通过比较实际的回报(包括立即奖励和折现后的未来奖励)和Q网络的预测来调整网络,以准确估计每个动作的价值。
- 该过程涉及考虑策略的熵(探索性),确保智能体在追求高回报的同时,也会考虑到策略的多样性。
-
策略网络的损失函数 L π ( θ ) L_{\pi}(\theta) Lπ(θ):
- 负责优化策略网络,即决定智能体在每个状态下应采取的最佳动作。
- 强调在保持行动的高熵(即多样性和探索性)的同时,选择预期回报最大化的动作。
- 策略网络通过最小化该损失函数来学习如何在探索和利用之间取得平衡。
L Q ( ϕ ) L_Q(\phi) LQ(ϕ)确保了对动作价值的准确估计,而 L π ( θ ) L_{\pi}(\theta) Lπ(θ)使智能体能够在探索多样动作的同时做出回报最大化的决策。两者共同作用使得智能体在复杂环境中能有效地学习和适应。
重参数化
熵正则化
代码实现
论文作者:https://github.com/rail-berkeley/softlearning
OpenAI:https://github.com/openai/spinningup

相关文章:

软性演员-评论家算法 SAC
软性演员-评论家算法 SAC 软性演员-评论家算法 SAC优势原理软性选择模型结构目标函数重参数化熵正则化代码实现 软性演员-评论家算法 SAC 优势原理 DDPG 的问题在于,训练不稳定、收敛差、依赖超参数、不适应复杂环境。 软性演员-评论家算法 SAC,更稳定…...

Nginx多域名部署多站点
目录 1.修改配置文件nginx.conf 2. 修改hosts文件 1.修改配置文件nginx.conf 在配置文件的 server_name 处修改成自己需要的域名,然后保存退出 j 查看语法是否错误,然后重启nginx nginx -t # 查看语法是否正确 systemctl restart nginx # 重启nginx …...

Java的常规面试题
Java的面试题主要涉及Java基础知识、并发编程、集合原理、JVM原理、I/O与网络编程、设计模式、互联网常用框架等多个领域[6]。一些常见的面试问题包括: 1. 面向对象的特征:继承、封装和多态性。 2. 访问修饰符public、private、protected以及默认时的区别…...

大数据技术发展史
文章目录 Google论文HadoopHive大数据生态 Google论文 今天我们常说的大数据技术,其实起源于Google在2004年前后发表的三篇论文,也就是我们经常听到的“三驾马车”,分别是分布式文件系统GFS、大数据分布式计算框架MapReduce和NoSQL数据库系统…...

linux常见基础指令
入门常见基础指令 ls、stat、 pwd 、cd、tree、 whoami、 touch、 mkdir、 rm 、 man、 cp、mv、cat、tac、echo、>、 >>、 < 、more、 less、 head、 tail、date、 cal、 find、 which、alias、whereis、grep、zip与unzip、 tar、bc、uname、xargs... 热键Tab、…...

“人家赚那么多”系列01:如何练习?练什么?
01 如何练习?练习什么? 今年计划重点围绕「在不骗自己的前提下,如何才能把事儿彻底做好,并做得有声有色?」为主题来写点儿东西,聊聊我是怎么做的,如何通过一些有效的方法来不断优化自己的。 想把…...

【Android】使用android studio查看内置数据库信息
要使用Android Studio查看内置数据库信息,可以按照以下步骤进行操作: 打开Android Studio并打开你的项目。 在左侧的Project窗口中,找到并展开你的app模块。 找到并展开"app" > "src" > "main"文件夹。…...

PHP开发日志 ━━ 基于PHP和JS的AES相互加密解密方法详解(CryptoJS) 适合CryptoJS4.0和PHP8.0
最近客户在做安全等保,需要后台登录密码采用加密方式,原来用个base64变形一下就算了,现在不行,一定要加密加key加盐~~ 前端使用Cypto-JS加密,传输给后端使用PHP解密,当然,前端虽然有key有盐&…...

2021-01-03 excel实现列递增,行保持不变
需求:excel文档数据操作的时候发现自动递增只能实现列不变行号递增 我这里里需要的是列递增行不变 解决方式:通过一些函数的组合使用 INDIRECT("驻场明细!"&CHAR(ROW()62)&ROW(驻场明细!A$28)) INDIRECT()函数的使用: INDI…...

[Python]两个杯子取水问题
利用两个杯子巧取三升水: 今天的这个趣味数学小游戏是利用两个没有刻度的水杯,巧妙地取出三升水来。 题目的条件是:一个总容量为6升的杯子和一个总容量为5升的杯子,同时面前有无限容量的水供你使用。不借助其它任何的容器…...

C++汇编语言学习计划
前几天买了某游戏的外挂,感觉外挂在我计算机上进行了不少操作,我想一探究竟,可是只有exe,没办法,翻译成汇编我也看不懂,索性来简单学习下。访问Chatgpt4,给了如下学习计划。 要从零开始学习C生成…...
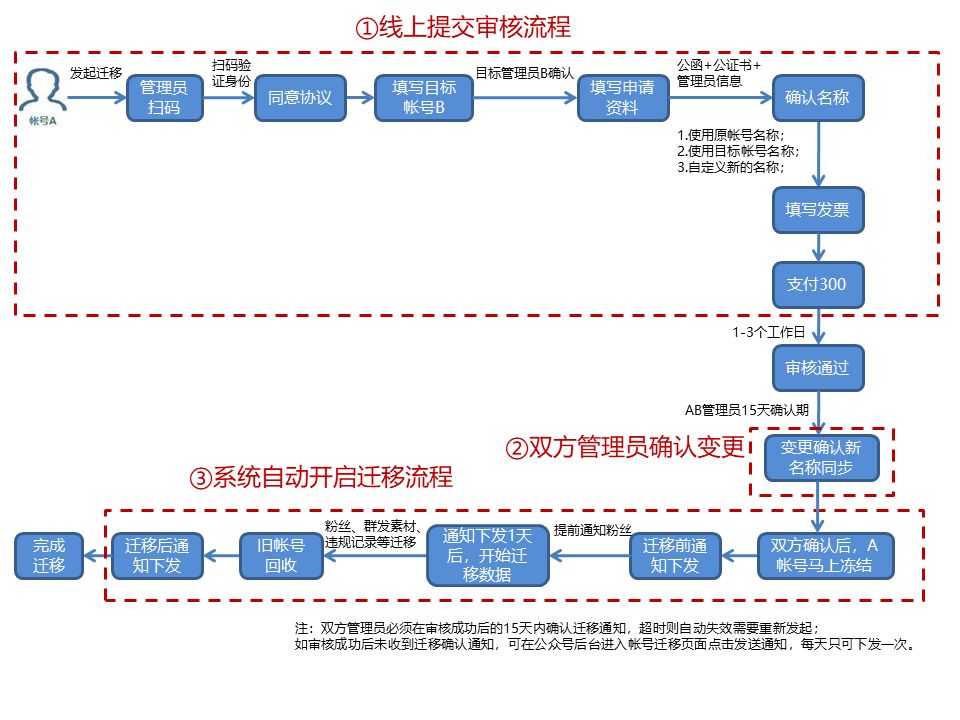
微信服务号升级订阅号条件
服务号和订阅号有什么区别?服务号转为订阅号有哪些作用?首先我们要看一下服务号和订阅号的主要区别。1、服务号推送的消息没有折叠,消息出现在聊天列表中,会像收到消息一样有提醒。而订阅号推送的消息是折叠的,“订阅号…...
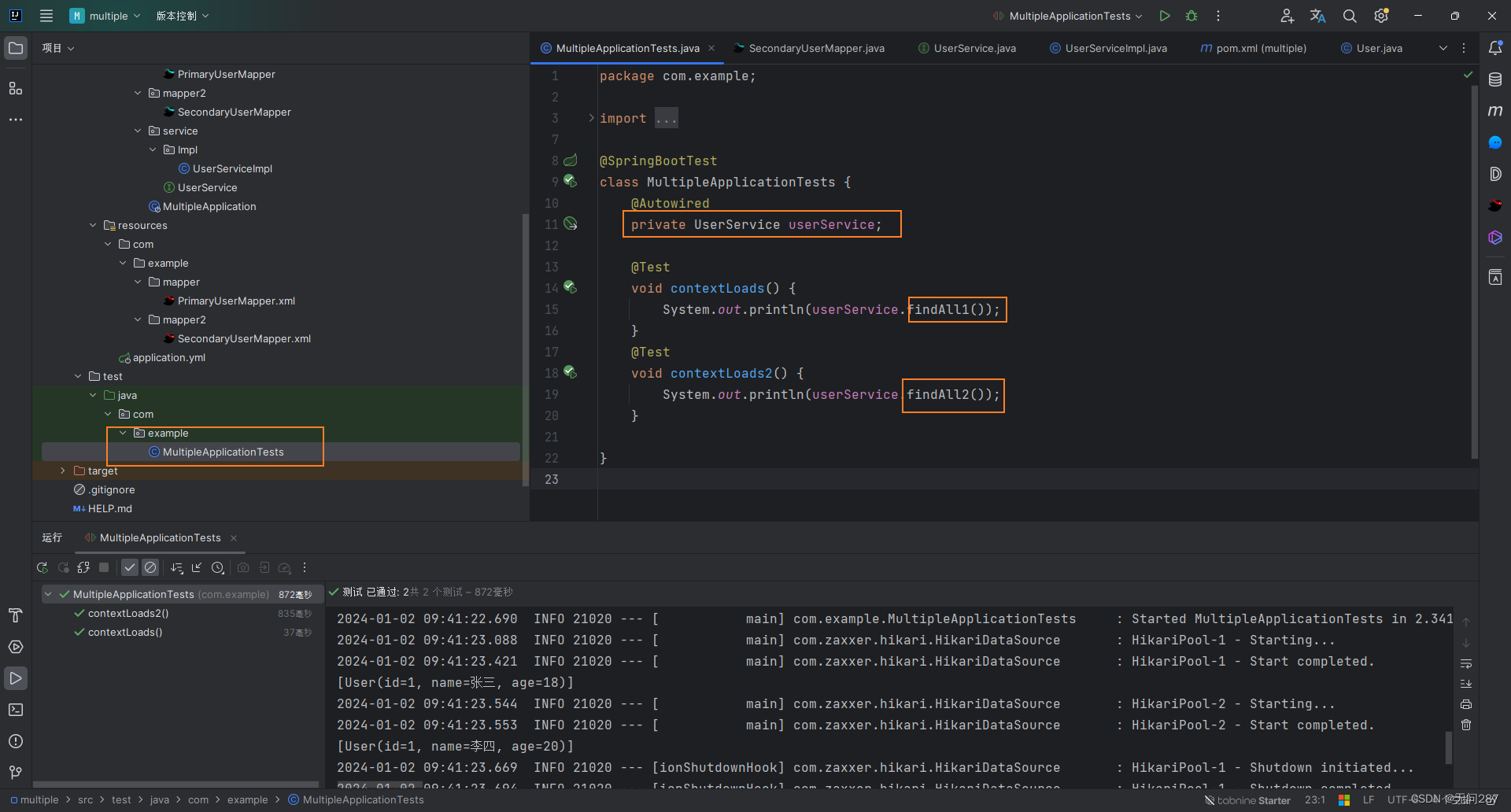
SpringBoot整合mybatis多数据源
废话不多说先上结果 对应数据库 首先导入所需的mybatis、mysql和lombok依赖 <dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId><version>2.2.2</version></dependen…...
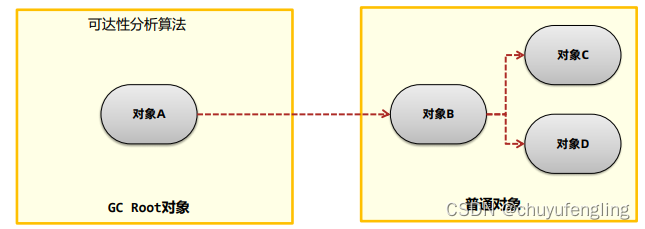
垃圾收集器与内存分配策略
内存分配和回收原则 对象优先在Eden区分配 大对象直接进入老年代 长期存活的对象进入老年代 什么是内存泄漏 不再使用的对象在系统中未被回收,内存泄漏的积累可能会导致内存溢出 自动垃圾回收与手动垃圾回收 自动垃圾回收:由虚拟机来自动回收对象…...

Python计算三角形的面积
Python 计算三角形的面积 以下实例为通过用户输入三角形三边长度,并计算三角形的面积: # 三角形第一边长 a 3 # 三角形第二边长 b 4 c float( input("输入三角形第三边长: ") ) # 计算半周长 s (a b c) / 2 # 计算…...
】万能字符单词拼写(JavaPythonC++JS实现))
198.【2023年华为OD机试真题(C卷)】万能字符单词拼写(JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-万能字符单词拼写二.解题思路三.题解代码Pytho…...

Tomcat服务为什么起不来?
转载说明:如果您喜欢这篇文章并打算转载它,请私信作者取得授权。感谢您喜爱本文,请文明转载,谢谢。 服务跑在Tomcat下面,有时候会遇到Tomcat起不来的情况。目前为止常遇到的情况有如下几种: 1. Tomcat服务…...
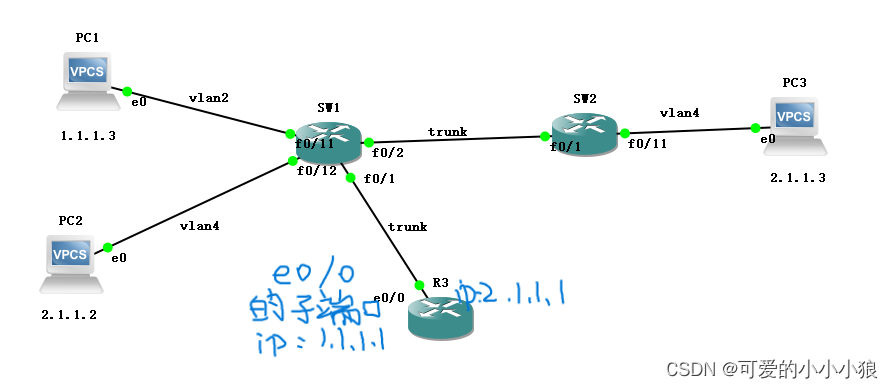
计算机网络 VLAN
路由器将多个局域网连接起来,而交换机将一个局域网里的设备连接起来。 路由器的端口分配局域网的网段(子网网段),局域网的内部设备的ip都在这个网段里,再由交换机将数据派发到目的设备,交换机是按照MAC地址…...
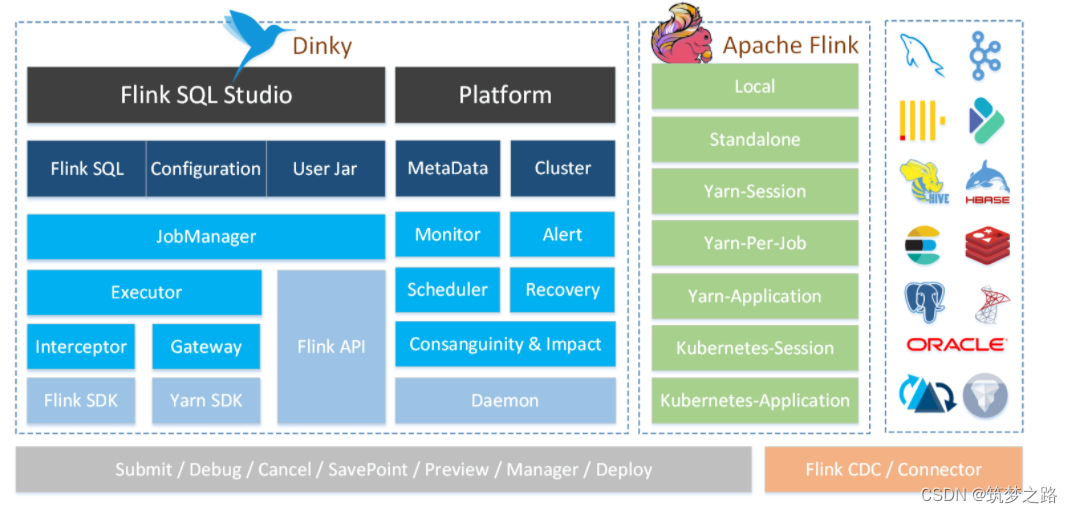
docker搭建Dinky —— 筑梦之路
简介 Dinky 是一个 开箱即用 、易扩展 ,以 Apache Flink 为基础,连接 OLAP 和 数据湖 等众多框架的 一站式 实时计算平台,致力于 流批一体 和 湖仓一体 的探索与实践。 主要功能 其主要功能如下: 沉浸式 FlinkSQL 数据开发&#x…...
)
Python基础(十四、数据容器之集合Set)
文章目录 一、集合语法二、集合的基本操作添加元素删除元素随机删除元素,可获得删除的值清空取出2个集合的差集消除2个集合的差集合并2个集合集合元素个数查询元素是否存在 遍历集合集合的遍历 什么是数据容器? 数据容器是Python中用于存储和操作数据的对…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
