【MPC学习笔记】01:MPC简介(Lecture 1_1 Unconstrained MPC)
本笔记来自北航诸兵老师的课程
课程地址:模型预测控制(2022春)lecture 1-1 Unconstrained MPC
文章目录
- 0 MPC 简介
- 0.1 案例引入
- 0.2 系统模型
- 0.3 MPC的优点
- 0.4 MPC的缺点
- 0.5 MPC的未来
- 1 详细介绍
0 MPC 简介
0.1 案例引入
MPC(Model Predictive Control)模型预测控制,是预测控制的一种,是基于模型来进行控制的。
老师举了下面这个例子来引入MPC的基本思想:
比方说我们为未来的一段时间制定计划,一天中几点到几点该做什么。但是计划赶不上变化,出现变化,出现拖延,计划就得做相应的调整。过了一段时间,根据计划的实际落实情况,再对接下来的计划进行调整。如此往复。不断地执行计划,也不断地修订计划。
0.2 系统模型
在控制系统中,有惯用表示:输入记作 u u u,状态变量记作 x x x,输出记作 y y y
假设系统是离散的,系统的状态方程为:
x ( k + 1 ) = f ( x ( k ) , u ( k ) ) x(k+1)=f(x(k),u(k)) x(k+1)=f(x(k),u(k))
实际上系统可以是,线性的或非线性的,连续的或离散的或既包含连续又包含离散的,确定的或随机的,只要满足该方程即可
设当前时刻为 k k k,当前状态为 x ( k ) x(k) x(k)
在输入 u ( k ) u(k) u(k) 的作用下,系统的状态将由 x ( k ) x(k) x(k) 变为 x ( k + 1 ) x(k+1) x(k+1)
在输入 u ( k + 1 ) u(k+1) u(k+1) 的作用下,系统的状态将由 x ( k + 1 ) x(k+1) x(k+1) 变为 x ( k + 2 ) x(k+2) x(k+2)
在输入 u ( k + 2 ) u(k+2) u(k+2) 的作用下,系统的状态将由 x ( k + 2 ) x(k+2) x(k+2) 变为 x ( k + 3 ) x(k+3) x(k+3)
…
由上面的列举,知:输入序列➡️输出序列
但在此时,也就是时刻 k k k ,我们并不知道输入序列 { u ( k ) , u ( k + 1 ) , u ( k + 2 ) , ⋯ } \{u(k),u(k+1),u(k+2),\cdots\} {u(k),u(k+1),u(k+2),⋯} 是多少
自然而然就会想到一个问题——怎么确定输入序列?
答:通过优化的方式,Optimization
将 状态序列 记为 X ( k ) X(k) X(k)
将 输入序列 记为 U ( k ) U(k) U(k)
输入序列的求解,可用如下优化问题的公式来描述:
U ∗ ( k ) = a r g m i n ∑ i = k ∞ l ( x ( i ) , u ( i ) ) = { u ∗ ( k ) , u ∗ ( k + 1 ) , … } s . t . x ∈ X , u ∈ U \begin{aligned} U^*(k) &= arg\ min\sum^{\infin}_{i=k}l(x(i),u(i)) \\ &=\{u^*(k),u^*(k+1),\dots\} \\ \\ s.t.\quad &x\in \mathscr{X}, u\in \mathscr {U} \end{aligned} U∗(k)s.t.=arg mini=k∑∞l(x(i),u(i))={u∗(k),u∗(k+1),…}x∈X,u∈U
其中, a r g m i n arg\ min arg min 表示使 **代价函数(目标函数)**取值最小时,输入序列 U ( k ) U(k) U(k) 的取值; ∗ ^* ∗ 表示最优解; s . t . s.t. s.t. 表示约束条件; l ( x ( i ) , u ( i ) ) l(x(i),u(i)) l(x(i),u(i)) 称为 “Stage cost”。
令 u ( k ) = u ∗ ( k ) u(k)=u^*(k) u(k)=u∗(k) ,舍弃求出的 U ∗ ( k ) U^*(k) U∗(k) 中后续其他时刻的输入,则由 x ( k + 1 ) = f ( x ( k ) , u ( k ) ) x(k+1) = f(x(k),u(k)) x(k+1)=f(x(k),u(k)) 可以求出时刻 k + 1 k+1 k+1 的状态
接着, k + 1 k+1 k+1 变为当前时刻,重复上述步骤,求出时刻 k + 2 k+2 k+2 的状态 x ( k + 2 ) x(k+2) x(k+2),…
以上就是MPC的基本原理
如果只优化一次,将计算出的 U ( k ) U(k) U(k) 序列依次执行,那么就变成了开环优化;而这里每一时刻优化后都只取 u ∗ ( k ) u^*(k) u∗(k) 执行( u ∗ ( k ) u^*(k) u∗(k)是 x ( k ) x(k) x(k)的函数),并且不断进行优化,构成滚动优化(闭环优化), 因此MPC实际上引入了反馈
0.3 MPC的优点
- 处理控制输入和系统状态上的约束(Constraints)
- 约束来源:actuator limits; safety; environmental; economic constraints
- PID没办法解决约束问题
- 近似最优控制
- 与线性系统中的最优控制(LQR, 线性二次型调节器)有区别,在LQR中,我们找到的是最优的增益 k k k(假设,已知系统是线性反馈),MPC找的是 u u u
0.4 MPC的缺点
- 需要在线优化(online optimization),可能会有较大的计算负载
0.5 MPC的未来
随着计算机算力提升,MPC或替代PID成为工业界控制主流

1 详细介绍
见【MPC学习笔记】02:MPC详细简介(Lecture 1_1 Unconstrained MPC)
相关文章:

【MPC学习笔记】01:MPC简介(Lecture 1_1 Unconstrained MPC)
本笔记来自北航诸兵老师的课程 课程地址:模型预测控制(2022春)lecture 1-1 Unconstrained MPC 文章目录 0 MPC 简介0.1 案例引入0.2 系统模型0.3 MPC的优点0.4 MPC的缺点0.5 MPC的未来 1 详细介绍 0 MPC 简介 0.1 案例引入 MPC(…...
c语言结构体学习上篇
文章目录 前言一、结构体的声明1,什么叫结构体?2,结构体的类型3,结构体变量的创建和初始化4,结构体的类型5,结构体的初始化 二、结构体的访问1,结构体成员的点操作符访问2,结构体体成员的指针访问 前言 昨…...

Linux: eBPF: bcc-tools:tcpdrop使用需要注意的问题
最近使用bcc-tools的时候注意到,bcc-tools(eBPF相关软件)的使用版本和内核的版本紧密程度非常高。因为要使用内核的函数或者结构体,所以就必须版本一致是必须的,不然会出现下面的警告或者错误: WARNING: tcp_drop() kernel function not found or traceable. The kernel …...

AI:113-基于卷积神经网络的图像风格迁移
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的关键代码,详细讲解供…...

15、Kubernetes核心技术 - 探针
目录 一、概述 二、探针类型 2.1、就绪探针(Readiness Probe) 2.2、存活探针(Liveness Probe) 三、探针探测方法 3.1、exec 3.2、httpGet 3.3、tcpSocket 四、探针配置项 五、探针使用 5.1、就绪探针(Readin…...

GTK4 环境配置
1 安装gtk4包裹: # sudo yum install gtk4 gtk4-devel gtk4-devel-docs devhelp glib2 glib2-devel glib2-doc 2 安装 glade 4 git clone https://github.com/ag-python/cambalache.git 记住 把软件目录 复制到 一个你不会移动删除的地方(千万别删除这个软件文件夹 因为运行…...

Yolov8部署——segmentation部署以及批量推理
Yolov8部署——segmentation部署以及批量推理 参考:在windows上部署Yolov8主要参考下面两个仓库,https://github.com/xunzixunzi/tensorrt-cpp-api和https://github.com/xunzixunzi/YOLOv8-TensorRT-CPP,代码说是适合批量处理,但是代码中是以…...

再见2023,你好2024!
大家好,我是老三,本来今天晚上打算出去转一转,陆家嘴打车实在太艰难了,一公里多的路,司机走了四十分钟,还没到,再加上身体不适,咳嗽地比较厉害,所以还是宅在酒店里&#…...
【计算机毕业设计】SSM二手交易网站
项目介绍 该项目分为前后台,前台普通用户角色,后台管理员角色。 管理员主要功能如下: 登陆,商品分类管理,商品管理,商品订单管理,用户管理等功能。 用户角色主要功能如下: 包含以下功能:查看所有商品,用户登陆注册…...

纠删码ReedSolomon
随着大数据技术的发展,HDFS作为Hadoop的核心模块之一得到了广泛的应用。为了数据的可靠性,HDFS通过多副本机制来保证。在HDFS中的每一份数据都有两个副本,1TB的原始数据需要占用3TB的磁盘空间,存储利用率只有1/3。而且系统中大部分…...
)
C++音视频开发技巧汇总(持续更新)
1.录制PCM数据 有时候我们需要录制PCM数据到文件以测试录制数据是否正确,一般可以使用以下代码实现: FILE *pf; fopen_s(&pf, "rec.pcm", "wb"); fwrite(myPcmArr, 1, outBufferLen, pf); 录制pcm文件后可以使用Audacity来导…...
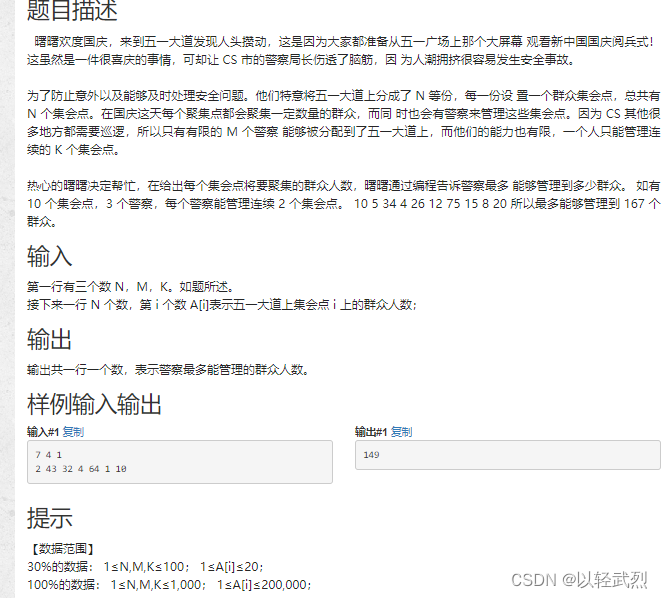
4462 4.曙曙献爱心
#include<bits/stdc.h> using namespace std; int n,m,k; int a[1001]; int s[1001]; int f[1001][1001];//f[i][j],i个警察,j个点,能管理的最大人数 int main(){cin>>n>>m>>k;for(int i1;i<n;i){cin>>a[i…...

浅谈命令模式
命令模式是一种行为设计模式,用于将一个请求封装成一个对象,从而使得请求的发送者和接收者解耦,并支持对请求进行参数化、队列化、撤销和重做等操作。 在命令模式中,有一下介个关键角色: Command(命令&am…...

软件测试/测试开发丨Python 模块与包
python 模块与包 python 模块 项目目录结构 组成 package包module模块function方法 模块定义 定义 包含python定义和语句的文件.py文件作为脚本运行 导入模块 import 模块名from <模块名> import <方法 | 变量 | 类>from <模块名> import * 注意&a…...
java企业网站系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java Web企业网站系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…...
MAC电脑安装java开发工具
一、安装brew 1.1、官网地址 链接 1.2、更新地址 二、安装 java brew install openjdk11 三、安装gradle Gradle安装与配置教程 - 知乎 四、GIT 4.1、GIT安装 brew install git 4.2、rsa ssh-keygen -t rsa -C "jhestarbucks.com" 五、自动搭建一个springBoot…...
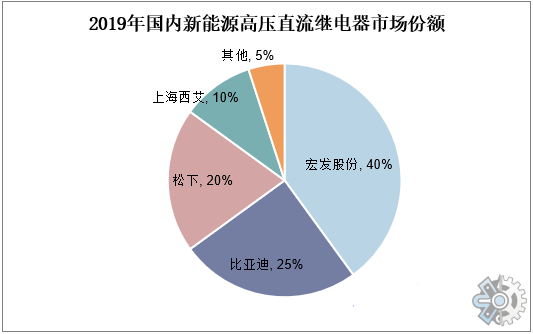
高压继电器,未来几年市场将保持稳定增长
高压继电器是一种用于控制大功率电气设备的开关装置,广泛应用于电力系统、轨道交通、工业自动化等领域。随着各行业对电气控制需求的不断增加,高压继电器市场也在不断扩大。全球高压继电器市场分析: 在全球市场中,目前主要的高压继…...

在Go语言中实现HTTP请求的缓存
大家好,我是你们可爱的编程小助手,今天我们要一起探讨如何使用Go语言实现HTTP请求的缓存。听起来是不是很酷?让我们开始吧! 首先,我们要明白什么是缓存。简单来说,缓存就是将数据存储在内存中,…...

技术扫盲:如何优雅的使用 java -jar
java -jar xxx.jar java -jar 是一个用于在命令行界面中执行 Java 可执行 JAR 文件的命令。它的语法如下: java -jar <JAR 文件路径> [参数]其中: java 是 Java 运行时环境的可执行文件。-jar 是一个选项,表示要执行的文件是一个 JA…...
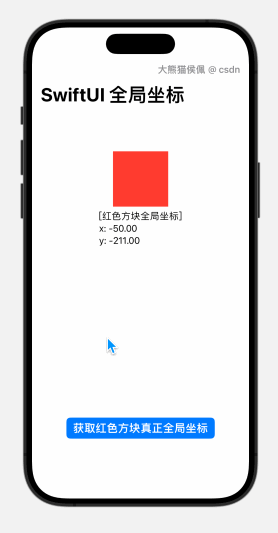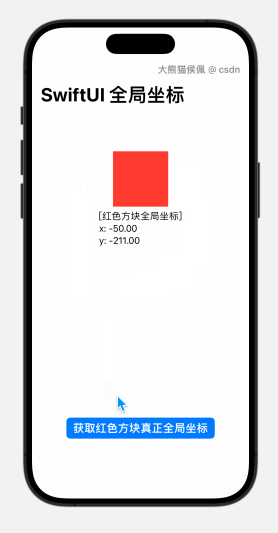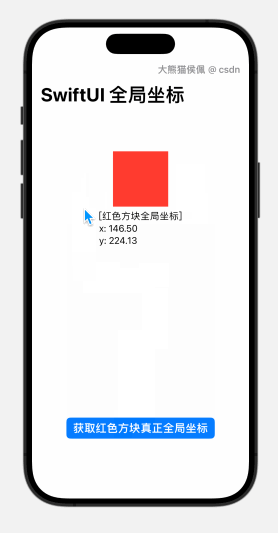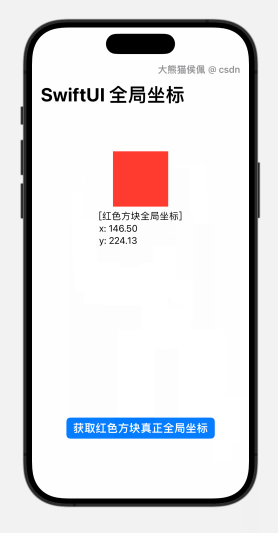
『番外篇七』SwiftUI 获取视图全局位置在 NavigationStack 中失效的解决方法
概览 在 番外篇六』SwiftUI 取得任意视图全局位置的三种方法 这篇博文里,我们详细讨论了在 SwiftUI 中获取任意视图全局坐标的几种方法。 不过,我们也从中提到了某些方法无法适用于 NavigationStack 视图,本篇博文由此应运而生。 在本篇博文种,您将学到如下内容: 概览1.…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
