SQL窗口函数大小详解
窗口大小
OVER 子句中的 frame_clause 选项用于指定一个滑动的窗口。窗口总是位于分区范围之内,是分区的一个子集。指定了窗口之后,分析函数不再基于分区进行计算,而是基于窗口内的数据进行计算。
指定窗口大小的语法如下:
ROWS | RANGE BETWEEN frame_start AND frame_end
其中,ROWS 表示以行为单位计算窗口的偏移量;RANGE 表示以数值为单位计算窗口的偏移量;
frame_start 用于定义窗口的起始位置,可以指定以下内容之一:
- UNBOUNDED PRECEDING,窗口从分区的第一行开始;
- N PRECEDING,窗口从当前行之前的第 N 行、范围 N 之内开始;
- CURRENT ROW,窗口从当前行开始。
frame_end 用于定义窗口的结束位置,可以指定以下内容之一:
-
CURRENT ROW,窗口到当前行结束;
-
M FOLLOWING,窗口到当前行之后的第 M 行、范围 M 之内结束;
-
UNBOUNDED FOLLOWING,窗口到分区的最后一行结束。
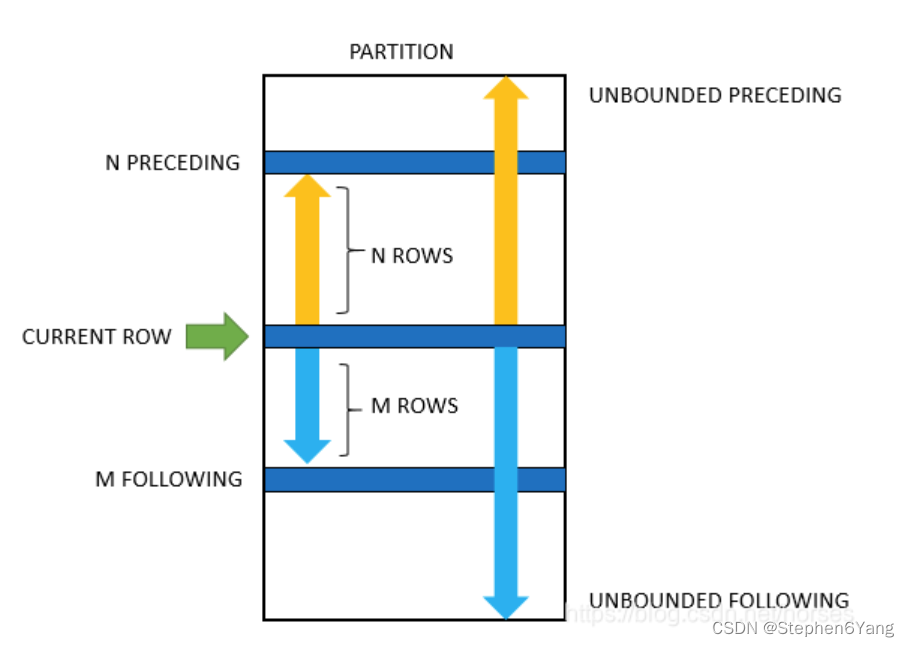

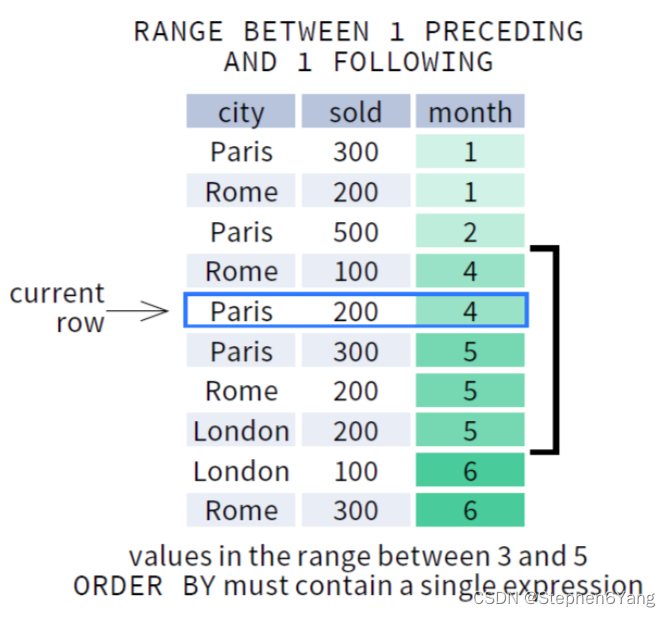
第一个窗口使用 ROWS 选项,包含了前后各 1 行以及当前行;第二个窗口使用 RANGE 选项,包含了当前行的数值减去 1(4-1=3)到当前行的数值加上 1(4+1=5)之间的所有数据;
如果没有指定窗口大小选项,默认使用的窗口如下:
- 如果指定了 ORDER BY, 默认窗口为 RANGE BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW;
- 如果没有指定 ORDER BY, 默认窗口为 ROWS BETWEEN UNBOUNDED PRECEDING AND UNBOUNDED FOLLOWING。
相关文章:

SQL窗口函数大小详解
窗口大小 OVER 子句中的 frame_clause 选项用于指定一个滑动的窗口。窗口总是位于分区范围之内,是分区的一个子集。指定了窗口之后,分析函数不再基于分区进行计算,而是基于窗口内的数据进行计算。 指定窗口大小的语法如下: ROWS…...

C#上位机与欧姆龙PLC的通信06---- HostLink协议(FINS版)
1、介绍 对于上位机开发来说,欧姆龙PLC支持的主要的协议有Hostlink协议,FinsTcp/Udp协议,EtherNetIP协议,本项目使用Hostlink协议。 Hostlink协议是欧姆龙PLC与上位机链接的公开协议。上位机通过发送Hostlink命令,可…...

认识SpringBoot项目中的Starter
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 循序渐进学SpringBoot ✨特色专栏&…...

ChatGPT 4.0真的值得花钱买入吗?
性能提升: ChatGPT 4.0的推出不仅意味着更先进的技术,还代表着更强大的性能。相较于3.5,4.0在处理任务时更为高效,响应更迅速。 更智能的理解: 随着版本的升级,ChatGPT 4.0对语境的理解能力得到了进一步的…...

vue3对比vue2是怎样的
一、前言 Vue 3通过引入Composition API、升级响应式系统、优化性能等一系列的改进和升级,提供了更好的开发体验和更好的性能,使得开发者能够更方便地开发出高质量的Web应用。它在Vue.js 2的基础上进行了一系列的改进和升级,以提供更好的性能、更好的开发体验和更好的扩展性…...

openGauss学习笔记-184 openGauss 数据库运维-升级-升级验证
文章目录 openGauss学习笔记-184 openGauss 数据库运维-升级-升级验证184.1 验证项目的检查表184.2 升级版本查询184.2.1 验证步骤 184.3 检查升级数据库状态184.3.1 验证步骤 openGauss学习笔记-184 openGauss 数据库运维-升级-升级验证 本章介绍升级完成后的验证操作。给出验…...
)
[Verilog语言入门教程] Verilog 减法器 (半减器, 全减器, 加减共用)
依公知及经验整理,原创保护,禁止转载。 专栏 《元带你学Verilog》 <<<< 返回总目录 <<<< “逻辑设计是一门艺术,它需要创造力和想象力。” - 马克张伯伦(Mark Zwolinski) 减法器是数字电路中常见的组件,用于减去两个二进制数的和。 在Verilog中…...

预编译仓库中的 Helm Chart
背景 内网部署项目, 没法直接hlem install , 需要提前看看有哪些镜像, 拉到本地看看 要使用预编译仓库中的 Helm Chart,你可以使用 helm fetch 命令来将 Chart 下载到本地,并使用 helm template 命令来预编译该 Chart。 首先,你可以使用以…...

Python requests get和post方法发送HTTP请求
requests.get() requests.get() 方法用于发送 HTTP GET 请求。下面介绍 requests.get() 方法的常用参数: url: 发送请求的 URL 地址。params: URL 中的查询参数,可以是字典或字符串。headers: 请求头信息。可以是字典类型,也可以是自定义的…...

在Cadence中单独添加或删除器件与修改网络的方法
首先需要在设置中使能 ,添加或修改逻辑选项。 添加或删除器件,点击logic-part,选择需要添加或删除的器件,这里的器件必须是PCB中已经有的器件,Refdes中输入添加或删除的器件标号,点击Add添加。 添加完成后就会显示在R1…...

轻松调整视频时长,创意与技术的新篇章
传统的视频剪辑工具往往难以精确控制时间,而【媒体梦工厂】凭借其先进的算法和界面设计,让视频时长的调整变得简单而精确,助你释放无限的创意,用技术为你的创意插上翅膀,让每一秒都有意义。 所需工具: 一…...

树与二叉树笔记整理
摘自小红书 ## 树与二叉树 ## 排序总结...

如何自动生成 API 接口文档 - 一份详细指南
本篇文章详细教你如何使用 Apifox 的 IDEA 插件实现自动生成接口代码。好处简单总结有以下几点: 自动生成接口文档: 不用手写,一键点击就可以自动生成文档,当有更新时,点击一下就可以自动同步接口文档;代码…...

【CF比赛记录】—— Good Bye 2023(A、B、C)
🌏博客主页:PH_modest的博客主页 🚩当前专栏:CF比赛记录 💌其他专栏: 🔴每日一题 🟡 cf闯关练习 🟢 C语言跬步积累 🌈座右铭:广积粮,缓…...
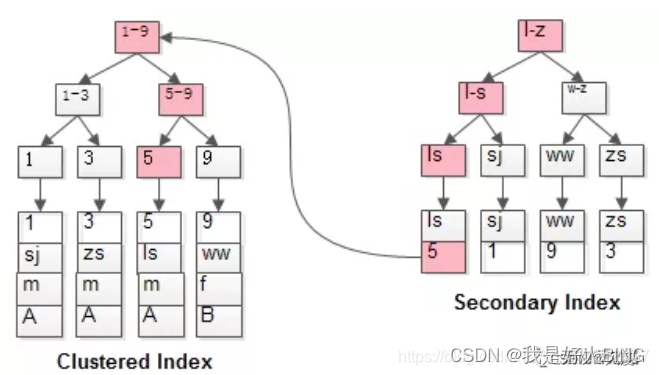
MySQL:索引
MySQL官方对索引的定义为: 索引 (Index) 是帮助MySQL高效获取数据的数据结构。 提取句子主干,就可以得到索引的本质:索引是数据结构。 1. 什么是索引,索引的作用 索引是一种用于快速查询和检索数据的数据结构,帮助mysql提高查询效率的数据…...
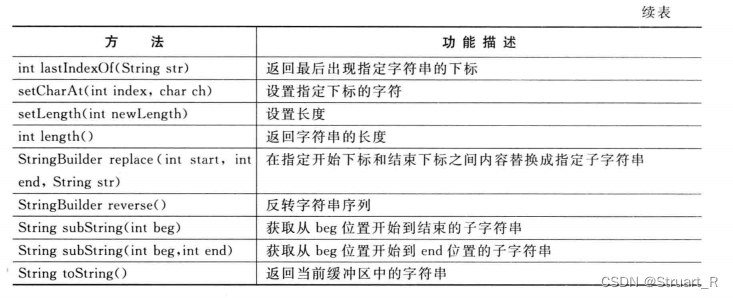
CUMT--Java复习--核心类
目录 一、装箱与拆箱 二、“”与equals 三、字符串类 1、String、StringBuffer、StringBuilder的区别 2、String类 3、StringBuffer类 4、StringBuilder类 四、类与类之间关系 一、装箱与拆箱 基本类型与对应封装类之间能够自动进行转换,本质就是Java的自…...
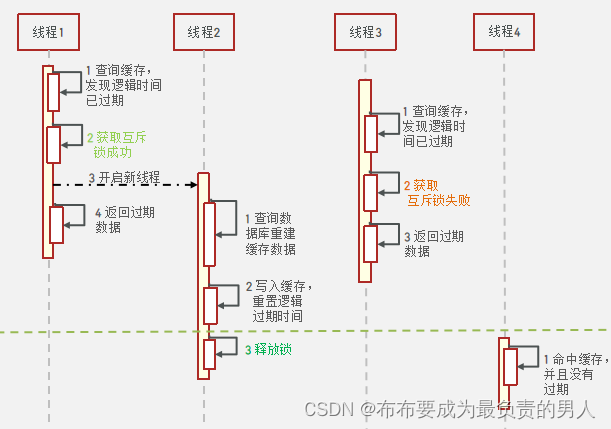
Redis:原理速成+项目实战——Redis实战4(解决Redis缓存穿透、雪崩、击穿)
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:Redis:原理项目实战——Redis实战3(Redis缓存最佳实践(问题解析高级实现)&#x…...
)
后端开发——jdbc的学习(一)
上篇结束了Mysql数据库的基本使用,本篇开始对JDBC进行学习总结,开始先简单介绍jdbc的基本使用,以及简单的练习;后续会继续更新!以下代码可以直接复制到idea中运行,便于理解和练习。 JDBC的概念 JDBC&#…...

阿里云免费SSL证书时长只有3个月,应对方法来了
阿里云免费SSL证书签发有效期从12个月缩短至3个月:尊敬的用户,根据供应商变更要求,免费证书(默认证书)的签发有效期将由12个月缩短至3个月。 免费证书(升级证书)的有效期不会改变。 没错&#…...
Flutter 中使用 ICON
Flutter Icon URL : https://fonts.google.com/icons: 在Flutter中使用 Icon 步骤如下: 导入图标库 在Dart 文件中导入 material.dart 包,该包包含了 Flutter 的图标库。 import package:flutter/material.dart;使用图标组件 …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
