2024美赛数学建模思路A题B题C题D题E题F题思路汇总 选题分析
文章目录
- 1 赛题思路
- 2 美赛比赛日期和时间
- 3 赛题类型
- 4 美赛常见数模问题
- 5 建模资料
1 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
2 美赛比赛日期和时间
比赛开始时间:北京时间2024年2月2日(周五)6:00
比赛结束时间:北京时间2024年2月6日(周二)9:00
提交截止日期:北京时间2024年2月6日10点(周二)
比赛结果:结果将于2024年5月31日或之前公布。
3 赛题类型
美国大学生数学建模竞赛目前分为两种类型,MCM(Mathematical Contest In Modeling)和 ICM(Interdisciplinary Contest In Modeling),两种类型竞赛采用统一标准进行,竞赛题目出来之后,参数队伍通过美赛官网进行选题,一共分为 6 种题型。
MCM:A:连续型 B:离散型 C:大数据
ICM:D:运筹学/网络科学 E:可持续性 F:政策
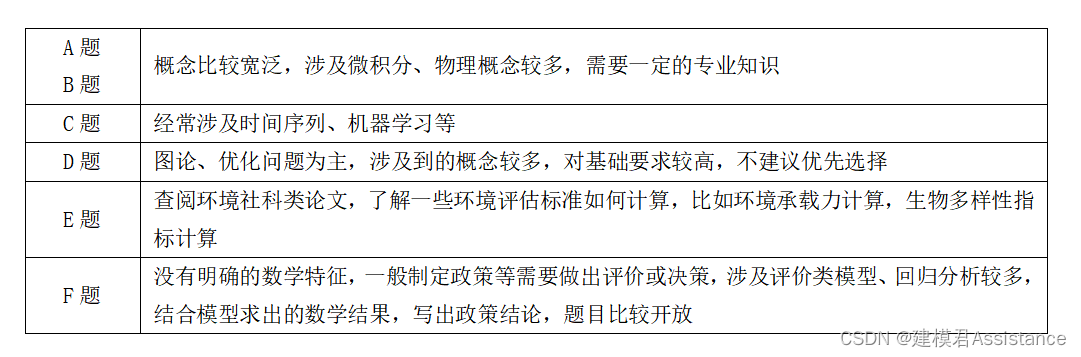
4 美赛常见数模问题
趁现在赛题还没更新,A君给大家汇总一下建模经常使用到的数学模型,题目八九不离十基本属于一下四种问题,对应的解法A君也相应给出
分别为:
- 分类模型
- 优化模型
- 预测模型
- 评价模型
4.1 分类问题
判别分析:
又称“分辨法”,是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。
其基本原理是按照一定的判别准则,建立一个或多个判别函数;用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标;据此即可确定某一样本属于何类。当得到一个新的样品数据,要确定该样品属于已知类型中哪一类,这类问题属于判别分析问题。
聚类分析:
聚类分析或聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集,这样让在同一个子集中的成员对象都有相似的一些属性,常见的包括在坐标系中更加短的空间距离等。
聚类分析本身不是某一种特定的算法,而是一个大体上的需要解决的任务。它可以通过不同的算法来实现,这些算法在理解集群的构成以及如何有效地找到它们等方面有很大的不同。
神经网络分类:
BP 神经网络是一种神经网络学习算法。其由输入层、中间层、输出层组成的阶层型神经网络,中间层可扩展为多层。RBF(径向基)神经网络:径向基函数(RBF-Radial Basis Function)神经网络是具有单隐层的三层前馈网络。它模拟了人脑中局部调整、相互覆盖接收域的神经网络结构。感知器神经网络:是一个具有单层计算神经元的神经网络,网络的传递函数是线性阈值单元。主要用来模拟人脑的感知特征。线性神经网络:是比较简单的一种神经网络,由一个或者多个线性神经元构成。采用线性函数作为传递函数,所以输出可以是任意值。自组织神经网络:自组织神经网络包括自组织竞争网络、自组织特征映射网络、学习向量量化等网络结构形式。K近邻算法: K最近邻分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
4.2 优化问题
线性规划:
研究线性约束条件下线性目标函数的极值问题的数学理论和方法。英文缩写LP。它是运筹学的一个重要分支,广泛应用于军事作战、经济分析、经营管理和工程技术等方面。建模方法:列出约束条件及目标函数;画出约束条件所表示的可行域;在可行域内求目标函数的最优解及最优值。
非线性规划:
非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。非线性规划研究一个 n元实函数在一组等式或不等式的约束条件下的极值问题,且 目标函数和约束条件至少有一个是未知量的非线性函数。目标函数和约束条件都是 线性函数的情形则属于线性规划。
整数规划:
规划中的变量(全部或部分)限制为整数,称为整数规划。若在线性模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法往往只适用于整数线性规划。一类要求问题的解中的全部或一部分变量为整数的数学规划。从约束条件的构成又可细分为线性,二次和非线性的整数规划。
动态规划:
包括背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等。
动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
多目标规划:
多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。任何多目标规划问题,都由两个基本部分组成:
(1)两个以上的目标函数;
(2)若干个约束条件。有n个决策变量,k个目标函数, m个约束方程,则:
Z=F(X)是k维函数向量,Φ(X)是m维函数向量;G是m维常数向量;
4.3 预测问题
回归拟合预测
拟合预测是建立一个模型去逼近实际数据序列的过程,适用于发展性的体系。建立模型时,通常都要指定一个有明确意义的时间原点和时间单位。而且,当t趋向于无穷大时,模型应当仍然有意义。将拟合预测单独作为一类体系研究,其意义在于强调其唯“象”性。一个预测模型的建立,要尽可能符合实际体系,这是拟合的原则。拟合的程度可以用最小二乘方、最大拟然性、最小绝对偏差来衡量。
灰色预测
灰色预测是就灰色系统所做的预测。是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
马尔科夫预测:是一种可以用来进行组织的内部人力资源供给预测的方法.它的基本 思想是找出过去人事变动的 规律,以此来推测未来的人事变动趋势.转换矩阵实际上是转换概率矩阵,描述的是组织中员工流入,流出和内部流动的整体形式,可以作为预测内部劳动力供给的基础.
BP神经网络预测
BP网络(Back-ProPagation Network)又称反向传播神经网络, 通过样本数据的训练,不断修正网络权值和阈值使误差函数沿负梯度方向下降,逼近期望输出。它是一种应用较为广泛的神经网络模型,多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
支持向量机法
支持向量机(SVM)也称为支持向量网络[1],是使用分类与回归分析来分析数据的监督学习模型及其相关的学习算法。在给定一组训练样本后,每个训练样本被标记为属于两个类别中的一个或另一个。支持向量机(SVM)的训练算法会创建一个将新的样本分配给两个类别之一的模型,使其成为非概率二元线性分类器(尽管在概率分类设置中,存在像普拉托校正这样的方法使用支持向量机)。支持向量机模型将样本表示为在空间中的映射的点,这样具有单一类别的样本能尽可能明显的间隔分开出来。所有这样新的样本映射到同一空间,就可以基于它们落在间隔的哪一侧来预测属于哪一类别。
4.4 评价问题
层次分析法
是指将一个复杂的 多目标决策问题 作为一个系统,将目标分解为多个目标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法。
优劣解距离法
又称理想解法,是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解,即各指标的最大值和最小值,通过计算每个方案到理想方案的相对贴近度,即靠近正理想解和远离负理想解的程度,来对方案进行排序,从而选出最优方案。
模糊综合评价法
是一种基于模糊数学的综合评标方法。 该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。 它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
灰色关联分析法(灰色综合评价法)
对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
典型相关分析法:是对互协方差矩阵的一种理解,是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
主成分分析法(降维)
是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。设法将原来变量重新组合成一组新的互相无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上用来降维的一种方法。
因子分析法(降维)
因子分析是指研究从变量群中提取共性因子的统计技术。最早由英国心理学家C.E.斯皮尔曼提出。他发现学生的各科成绩之间存在着一定的相关性,一科成绩好的学生,往往其他各科成绩也比较好,从而推想是否存在某些潜在的共性因子,或称某些一般智力条件影响着学生的学习成绩。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设。
BP神经网络综合评价法
是一种按误差逆传播算法训练的多层前馈网络,是应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。
5 建模资料
资料分享: 最强建模资料


相关文章:

2024美赛数学建模思路A题B题C题D题E题F题思路汇总 选题分析
文章目录 1 赛题思路2 美赛比赛日期和时间3 赛题类型4 美赛常见数模问题5 建模资料 1 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 2 美赛比赛日期和时间 比赛开始时间:北京时间2024年2月2日(周五ÿ…...

C++ 常用设计模式
一、工厂模式 from:C开发常用的设计模式及其实现详解 - 知乎 摘抄: 简单工厂、工厂、抽象工厂: 简单工厂需要工厂内部判断,而工厂模式不需要修改工厂类: 抽象工厂: 接上图: 未完待续.........

高性价比的高速吹风机/高速风筒解决方案,基于普冉单片机开发
高速吹风机是近些年非常火的一款产品,快速崛起并颠覆了传统吹风机,高速吹风机也成为了传统吹风机替代的一个大趋势。高速吹风机是利用高转速产生的大风量来快速吹干头发,由于其精巧的外观设计、超低的噪声、出色的干发效果,高速吹…...

toRefs的用法
文章目录 toRefs是什么toRefs的作用以及为什么要用它? toRefs是什么 toRefs 是 Vue 3 Composition API 中的一个函数,它用于将响应式对象转换为普通对象,其中对象的每个属性都是 ref 对象。这是因为在 Vue 3 中,reactive 创建的对…...
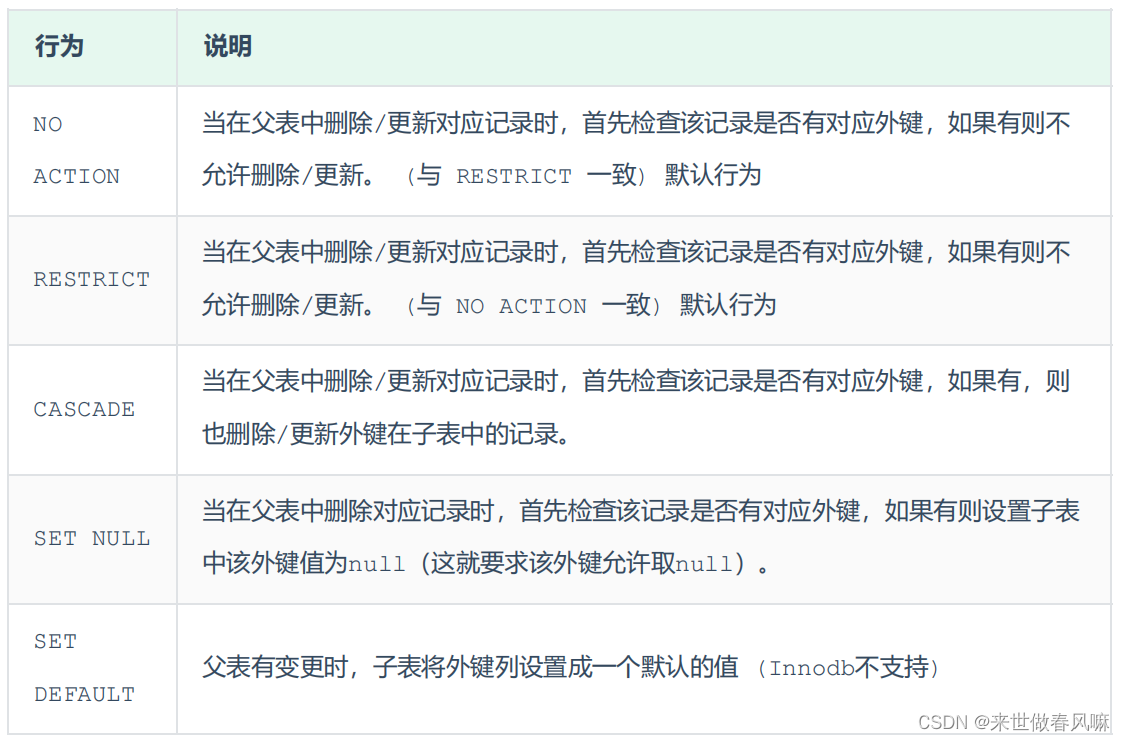
MySQL基础篇(三)约束
一、概述 概念:约束是作用于表中字段上的规则,用于限制存储在表中的数据。 目的:保证数据库中数据的正确、有效性和完整性。 分类: 注意:约束是作用于表中字段上的,可以在创建表/修改表的时候添加约束。 二…...
Java进阶 1-2 枚举
目录 常量特定方法 职责链模式的枚举实现 状态机模式的枚举实现 多路分发 1、使用枚举类型实现分发 2、使用常量特定方法实现分发 3、使用EnumMap实现分发 4、使用二维数组实现分发 本笔记参考自: 《On Java 中文版》 常量特定方法 在Java中,我们…...

一个人最大的内驱力是什么?
1、不因为孤独或外界压力而降低「生活标准“」的能力。 ”因为寂寞去约炮“、“因为家里催婚匆忙结婚“、”因为没谈过恋爱随便找个人交往。 “你的每一次选择都是在为自己想要的世界而投的票,往后余生是幸福还是悲剧,就是在这一次次 的将就与坚持死磕中…...

解决方法:公众号的API上传素材报错40005
公众号的API上传素材报错40005 Error uploading file : {"errcode":40005,"errmsg":"invalid file type hint: [YOkxGA0122w487] rid: 223442-323247e7bd5-5d75322d88"}上传错误原因分析: 之前成功的示例,文件名为"…...

音量控制软件sound control mac功能亮点
sound control mac可以帮助用户控制某个独立应用程序的音量,通过每应用音量,均衡器,平衡和音频路由独立控制每个应用的音频,还有整个系统的音量。 sound control mac功能亮点 每个应用程序的音量控制 独立控制应用的数量。 键盘音…...

Spring Boot 生产就绪中文文档-下
本文为官方文档直译版本。原文链接 由于篇幅较长,遂分两篇。上半部分中文文档 Spring Boot 生产就绪中文文档-下 度量标准入门受支持的监控系统AppOpticsAtlasDatadogDynatracev2 API自动配置手动配置 v1 API (旧版)与版本无关的设置 ElasticGangliaGraphiteHumioIn…...

DS|树结构及应用
题目一:DS树 -- 树的先根遍历(双亲转先序) 题目描述: 给出一棵树的双亲表示法结果,用一个二维数组表示,位置下标从0开始,如果双亲位置为-1则表示该结点为根结点 编写程序,输出该树…...
Java 读取超大excel文件
注意:此参考解决方案只是针对xlsx格式的excel文件! Maven <dependency><groupId>com.monitorjbl</groupId><artifactId>xlsx-streamer</artifactId><version>2.2.0</version> </dependency>读取方式1…...

K8S中的job和CronJob
Job 介绍 Kubernetes jobs主要是针对短时和批量的工作负载。它是为了结束而运行的,而不是像deployment、replicasets、replication controllers和DaemonSets等其他对象那样持续运行。 示例 apiVersion: batch/v1 kind: Job metadata:name: pispec:template:spec:r…...
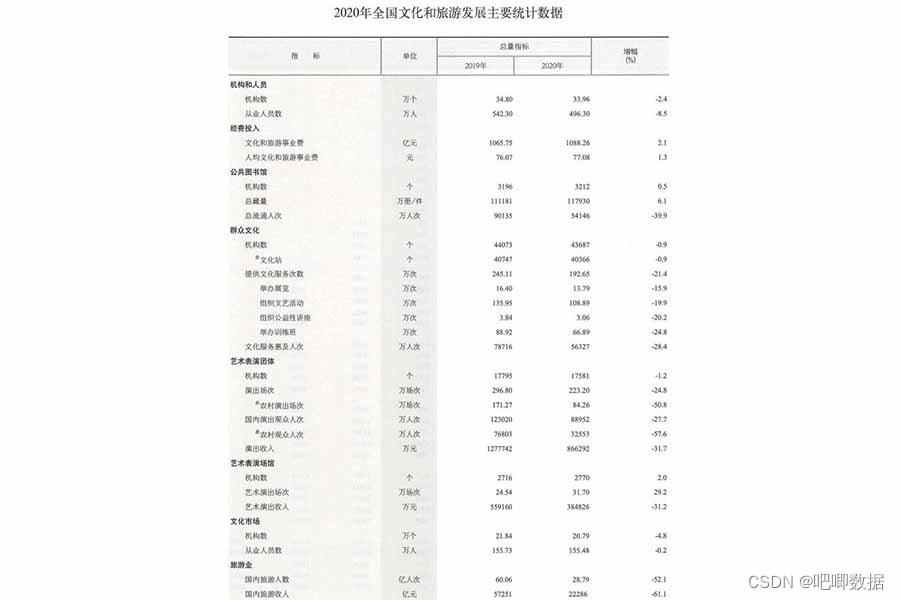
中国文化文物和旅游统计年鉴,数据含pdf、excel等格式,文本形式呈现,可预览数据
基本信息. 数据名称: 中国旅游统计年鉴 数据格式: pdf、xls不定 数据时间: 2012-2020年 数据几何类型: 文本 数据坐标系: —— 数据来源:文化和旅游部、网络公开数据 原名为《中国旅游统计年鉴》2020年后更名为《中国文化文物和旅游统计年鉴》ÿ…...
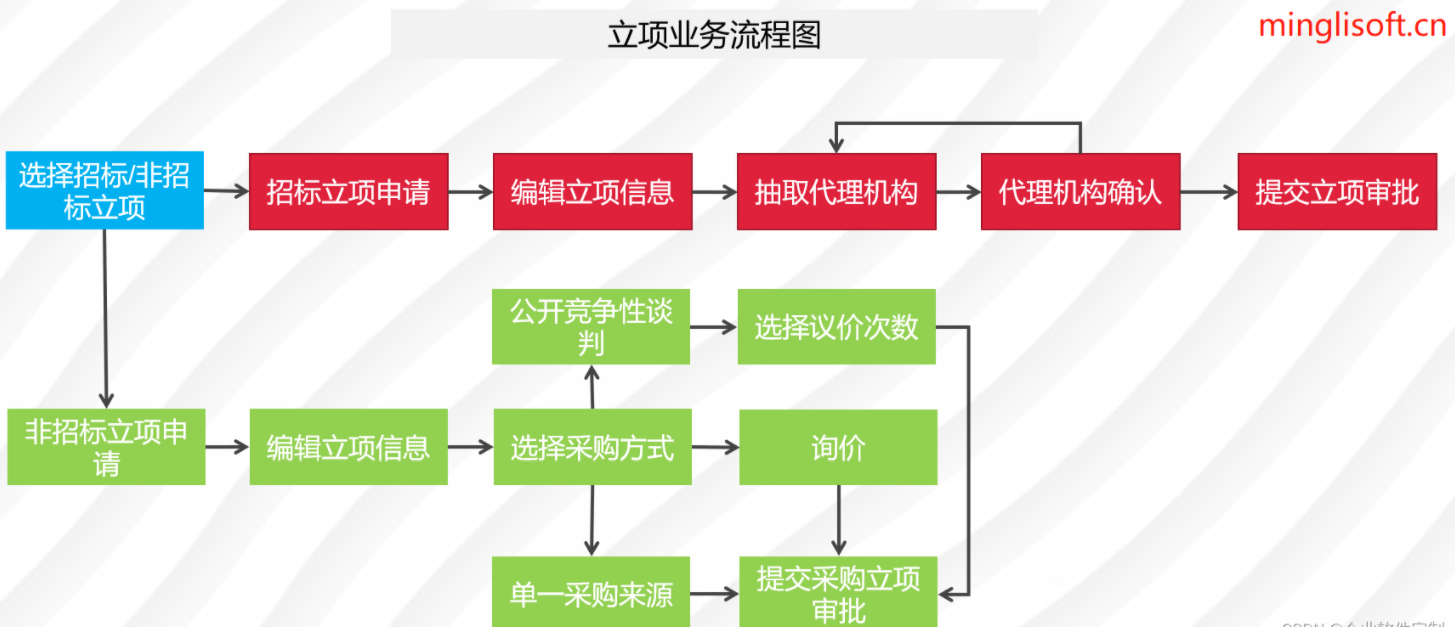
Java版企业电子招标采购系统源码——鸿鹄电子招投标系统的技术特点
在数字化时代,采购管理也正经历着前所未有的变革。全过程数字化采购管理成为了企业追求高效、透明和规范的关键。该系统通过Spring Cloud、Spring Boot2、Mybatis等先进技术,打造了从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通过…...

go语言语法基础
文章目录 前言一、输入和输出常用的字符串格式化符号 二、注释三、Go常用基本语言数据类型数字类型布尔类型字符类型变量与常量数组和切片数组切片 map类型创建map增删改查特别提醒 指针 四、运算符五、条件判断语句if系列switch六、循环语句for循环标准写法死循环while循环do …...

eclipse 和java环境的安装教程
安装 Eclipse 和配置 Java 环境是一个多步骤的过程,涉及到安装 Java Development Kit (JDK) 和 Eclipse IDE。以下是基本步骤: 安装 Java Development Kit (JDK) 下载 JDK: 访问 Oracle 官方网站(Oracle JDK)或者选择…...

Win11系统的优化方法参考文档(彻底优化策略)
目录 一、个性化-应用-关闭防火墙等的设置 二、任务栏优化设置 三、Win11开始菜单更改为Win10经典菜单 四、将Micresoft Store 从固定任务栏取消 五、电源性能优化 六、解决卡顿 七、卸载系统自带软件 八、任务管理器开机启动项的禁用 九、调整为最佳性能 十…...
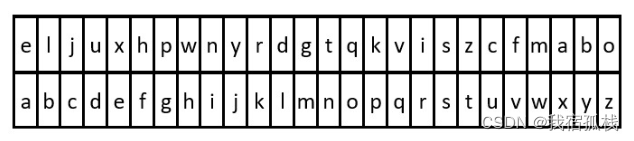
Leetcode13-解密消息(2325)
1、题目 给你字符串 key 和 message ,分别表示一个加密密钥和一段加密消息。解密 message 的步骤如下: 使用 key 中 26 个英文小写字母第一次出现的顺序作为替换表中的字母 顺序 。 将替换表与普通英文字母表对齐,形成对照表。 按照对照表 …...
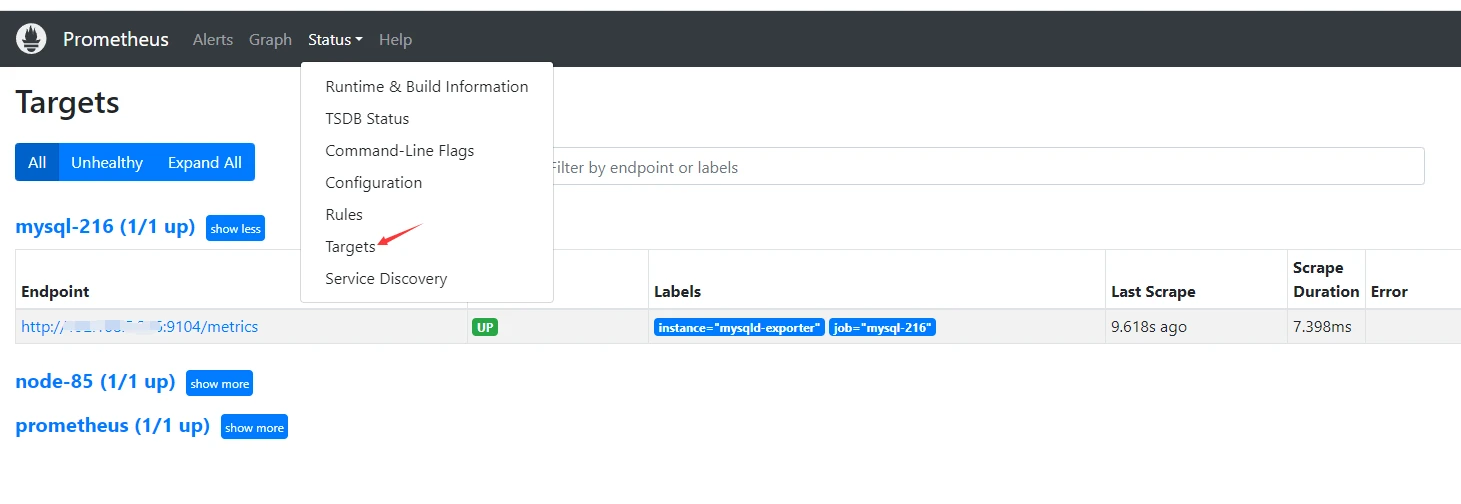
二进制安装包安装Prometheus插件安装(mysql_exporter)
简介 mysql_exporter是用来收集MysQL或者Mariadb数据库相关指标的,mysql_exporter需要连接到数据库并有相关权限。既可以用二进制安装部署,也可以通过容器形式部署,但为了数据收集的准确性,推荐二进制安装。 一,下载安…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
