MATLAB - MPC - 优化问题(Optimization Problem)
系列文章目录
前言
模型预测控制可在每个控制间隔内解决一个优化问题,具体来说就是二次规划(QP)。求解结果决定了被控对象在下一个控制间隔之前使用的操纵变量(MV)。
该 QP 问题具有以下特点:
- 目标或 "成本 "函数 - 要最小化的控制器性能的非负标量。
- 约束条件 - 解决方案必须满足的条件,如 MV 和被控对象输出变量的物理边界。
- 决策 - 在满足约束条件的同时使成本函数最小化的 MV 调整。
下文将详细介绍这些功能。
一、标准代价函数
标准成本函数是四个项的总和,每个项都侧重于控制器性能的一个特定方面,如下所示:
这里,zk 是 QP 决策。如下所述,每个项都包含权重,可帮助您平衡相互竞争的目标。虽然 MPC 控制器提供了默认权重,但您通常需要对其进行调整,以适应您的应用。
1.1 输出参考跟踪
在大多数应用中,控制器必须将选定的被控对象输出保持在或接近指定的参考值。MPC 控制器使用以下标量性能指标进行输出参考跟踪:
此处
- k - 当前控制间隔。
- p - 预测范围(区间数)。
- ny - 被控对象输出变量的个数。
- zk - QP 决策,取值为
- yj(k+i|k) - 第 j 个被控对象在第 i 个预测水平步的输出预测值,单位为工程单位。
- rj(k+i|k) - 第 j 个被控对象在第 i 个预测水平步的输出参考值,单位为工程单位。
- 第 j 个被控对象产量的比例因子,单位为工程单位。
- 第 i 个预测水平步的第 j 个被控对象输出的调整权重(无量纲)。
值 ny、p、 和
是恒定的控制器规格。控制器接收整个预测范围内的参考值 rj(k+i|k)。控制器使用状态观测器来预测被控对象的输出 yj(k+i|k),这些输出取决于受控变量调整 (zk)、测量干扰 (MD) 和状态估计值。在间隔 k 时,可获得控制器状态估计值和 MD 值。因此,Jy 仅是 zk 的函数。
1.2 操纵变量跟踪
在某些应用中,例如当被控对象的输出多于操纵变量时,控制器必须将选定的操纵变量 (MV) 保持在或接近指定的目标值。MPC 控制器使用以下标量性能指标进行操纵变量跟踪:
此处
- k - 当前控制间隔。
- p - 预测范围(区间数)。
- nu - 受控变量的数量。
- zk - QP 决策,取值为
- uj,target(k+i|k) - 第 j 个 MV 在第 i 个预测水平步的目标值,单位为工程单位。
- 第 j 个 MV 的比例因子,单位为工程单位。
- 第 j 个 MV 在第 i 个预测水平步的调整权重(无量纲)。
数值 nu、p、 和
是恒定的控制器规格。控制器接收整个范围内的 uj,target(k+i|k) 值。控制器利用状态观测器预测被控对象的输出。因此,Ju 只是 zk 的函数。
1.3 操纵变量移动抑制
大多数应用都喜欢小的 MV 调整(移动)。MPC 常量使用以下标量性能指标来抑制操纵变量移动:
此处
- k - 当前控制间隔。
- p - 预测范围(区间数)。
- ny - 被控对象输出变量的个数。
- zk - QP 决策,取值为
- 第 j 个 MV 的比例因子,单位为工程单位。
- 第 j 个 MV 运动在第 i 个预测水平步的调整权重(无量纲)。
的值是控制器的常数。u(k-1|k) = u(k-1),是上一个控制区间的已知 MV。JΔu 仅是 zk 的函数。
此外,控制区间 m < p(或 MV 阻塞)会限制某些 MV 移动为零。
1.4 违反约束
在实践中,违反约束可能是不可避免的。软约束允许在这种情况下获得可行的 QP 解决方案。MPC 控制器采用一个无量纲、非负的松弛变量 εk,它量化了最坏情况下的约束违规。(见约束条件)相应的性能指标为
这里
zk - QP 决策,取值为
εk - 控制区间 k 的松弛变量(无量纲)。
ρε - 违反约束条件的惩罚权重(无量纲)。
二、 替代成本函数
您可以选择使用以下替代标准成本函数的方法:
这里,Q(ny-by-ny)、Ru 和 RΔu(nu-by-nu)是正半无穷权重矩阵,并且:
也是、
Sy - 被控对象输出可变比例系数的对角矩阵,单位为工程单位。
Su - 以工程单位表示的 MV 比例因子对角矩阵。
r(k+1|k) - 第 i 个预测水平步的 ny 个被控对象输出参考值,单位为工程单位。
y(k+1|k) - 第 i 个预测水平步的 ny 个被控对象的工厂产出,单位为工程单位。
zk - QP 决策,取值为
utarget(k+i|k) - u(k+i|k) 对应的 nu MV 目标值,单位为工程单位。
与标准成本函数一样,输出预测使用状态观测器。
替代成本函数允许非对角线加权,但要求每个预测水平步的权重相同。
如果满足以下条件,替代成本函数和标准成本函数是相同的:
- 标准成本函数采用的权重 w , 和 w 相对于指数 i = 1:p 是常数。
- 矩阵 Q、Ru 和 RΔu 是对角线,对角元素是这些权重的平方。
三、约束条件
某些约束条件是隐含的。例如,控制范围 m < p(或 MV 阻塞)会强制某些 MV 增量为零,而用于被控对象输出预测的状态观测器是一组隐式相等约束。您可以配置的显式约束如下所述。
3.1 被控对象输出、MV 和 MV 增量的界限
最常见的 MPC 约束是边界,如下所示。
这里的 V 参数(ECR 值)是无量纲控制器常数,类似于成本函数权重,但用于约束软化(参见约束软化)。此外还有
εk - 用于约束软化的标量 QP 松弛变量(无量纲)。
syj - 第 j 个被控对象输出的比例因子,单位为工程单位。
suj - 第 j 个 MV 的比例因子,单位为工程单位。
yj,min(i)、yj,max(i) - 第 j 个被控对象在第 i 个预测水平步的产量下限和上限,单位为工程单位。
uj,min(i)、uj,max(i) - 第 j 个 MV 在第 i 个预测水平步的下限和上限,单位为工程单位。
Δuj,min(i)、Δuj,max(i) - 第 i 个预测水平步的第 j 个 MV 增量的下限和上限,单位为工程单位。
除松弛变量非负条件外,上述所有约束条件都是可选的,默认为非活动状态(即初始化为无限极限值)。要包含约束条件,必须在设计控制器时指定有限极限值。
四、QP 矩阵
本节介绍与优化问题中描述的模型预测控制优化问题相关的矩阵。
4.1 预测
假设输入干扰模型中描述的干扰模型为单位增益,即 d(k) = nd(k) 为白高斯噪声。可以将此问题表示为
那么,预测模型就是
接下来,考虑预测模型在时间 k=0 时的未来轨迹问题。对所有预测时刻 i 设置 nd(i)=0,得到
该方程给出的解是
其中
4.2 优化变量
设 m 为自由控制移动的次数,设 z= [z0; ...; zm-1]。那么
其中,JM 取决于阻塞动作的选择。z0、......、zm-1 与松弛变量ɛ 一起构成了优化问题的自由优化变量。在系统只有一个操纵变量的情况下,z0、......、zm-1 是标量。
考虑下图中描述的阻塞动作。
阻塞移动: 移动 = [2 3 2] 的输入和输入增量
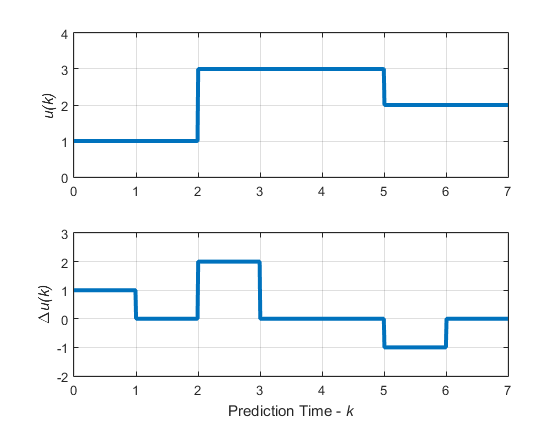
这个图形对应于选择 moves=[2 3 2],或者等价于 u(0)=u(1),u(2)=u(3)=u(4),u(5)=u(6),Δ u(0)=z0,Δ u(2)=z1,Δ u(5)=z2,Δ u(1)=Δ u(3)=Δ u(4)=Δ u(6)=0.
那么,相应的矩阵 JM 为
有关操纵变量阻塞的更多信息,请参阅操纵变量阻塞。
4.3 成本函数
标准形式。 要优化的函数是
其中
最后,在代入 u(k)、Δu(k)、y(k)之后,J(z) 可重写为
其中
注意事项
您可能希望 QP 问题保持严格的凸性。如果 Hessian 矩阵 KΔU 的条件数大于 1012,请在每个对角项上添加 10*sqrt(eps)。只有当所有输入率都未受惩罚(WΔu=0)时,才能使用此解决方案(请参阅 mpc 对象的权重属性)。
替代成本函数。 如果使用 "替代成本函数 "中所示的替代成本函数,则等式 1 由以下公式代替:
在这种情况下,分块对角矩阵重复 p 次,例如,预测范围内每一步重复一次。
您也可以选择使用标准形式和替代形式的组合。更多信息,请参阅 mpc 对象的权重属性。
约束条件 接下来,考虑输入、输入增量和输出的限制以及约束条件 ɛ≥ 0。
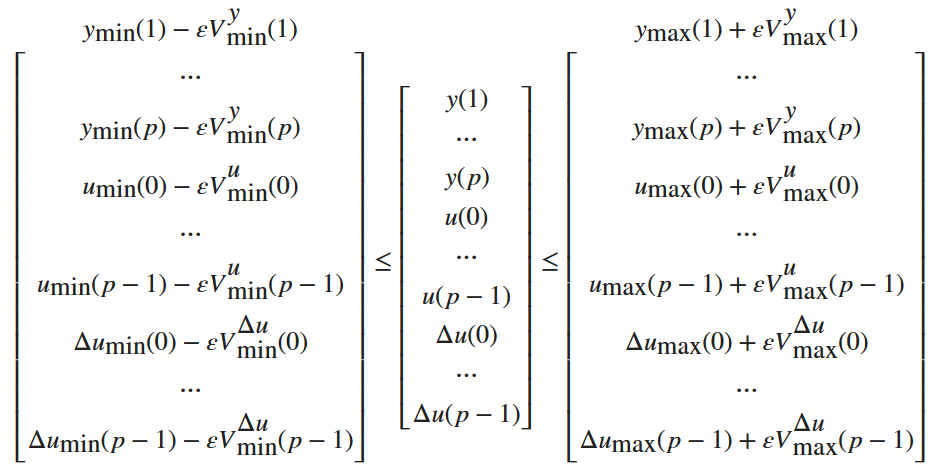
注释
为减少计算量,控制器会自动消除无关的约束条件,如无限边界。因此,实时使用的约束集可能远小于本节建议的约束集。
与计算成本函数类似,可以将 u(k)、Δu(k)、y(k) 代入,得到
相关文章:
MATLAB - MPC - 优化问题(Optimization Problem)
系列文章目录 前言 模型预测控制可在每个控制间隔内解决一个优化问题,具体来说就是二次规划(QP)。求解结果决定了被控对象在下一个控制间隔之前使用的操纵变量(MV)。 该 QP 问题具有以下特点: 目标或 "成本 "函数 - …...

机器学习中的概念 张量、标量、向量、矩阵等数据结构的区别
张量、标量、向量和矩阵等数据结构在深度学习和数学中扮演着重要角色,它们之间的区别如下: 标量(Scalar):标量是一个单独的数,它没有方向,只有大小。在深度学习中,标量通常表示一个…...
eureka注册列表 某服务出现多个服务实例
最近文件导出功能偶发成功,大部分情况都失败,开始以为接口被拦截,gateway服务没有接口调用日志,发现测试环境可以,正式环境功能无法正常使用。 偶然看到注册中心如下 发现file服务有3个实例,调用接口将错误…...
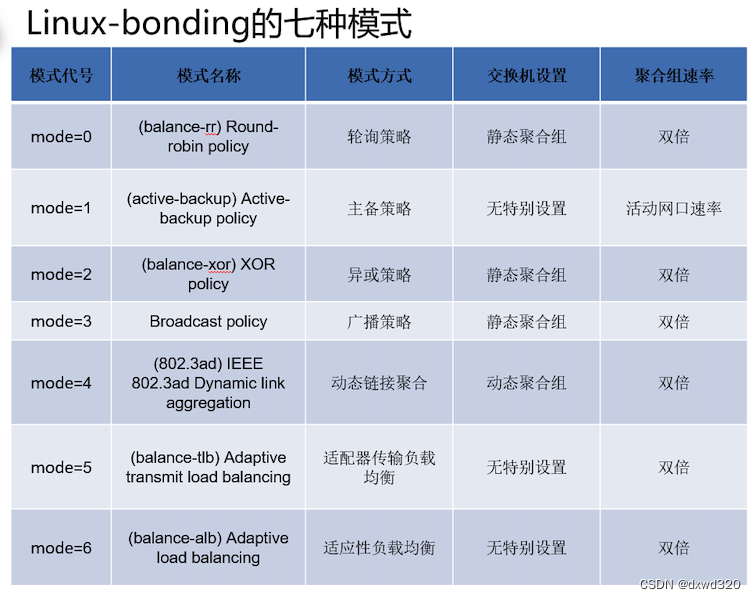
ubuntu22.04配置双网卡绑定提升带宽
这里写自定义目录标题 Bonding简介配置验证参考链接 Bonding简介 bonding(绑定)是一种linux系统下的网卡绑定技术,可以把服务器上n个物理网卡在系统内部抽象(绑定)成一个逻辑上的网卡,能够提升网络吞吐量、实现网络冗余、负载均衡等功能,有很…...
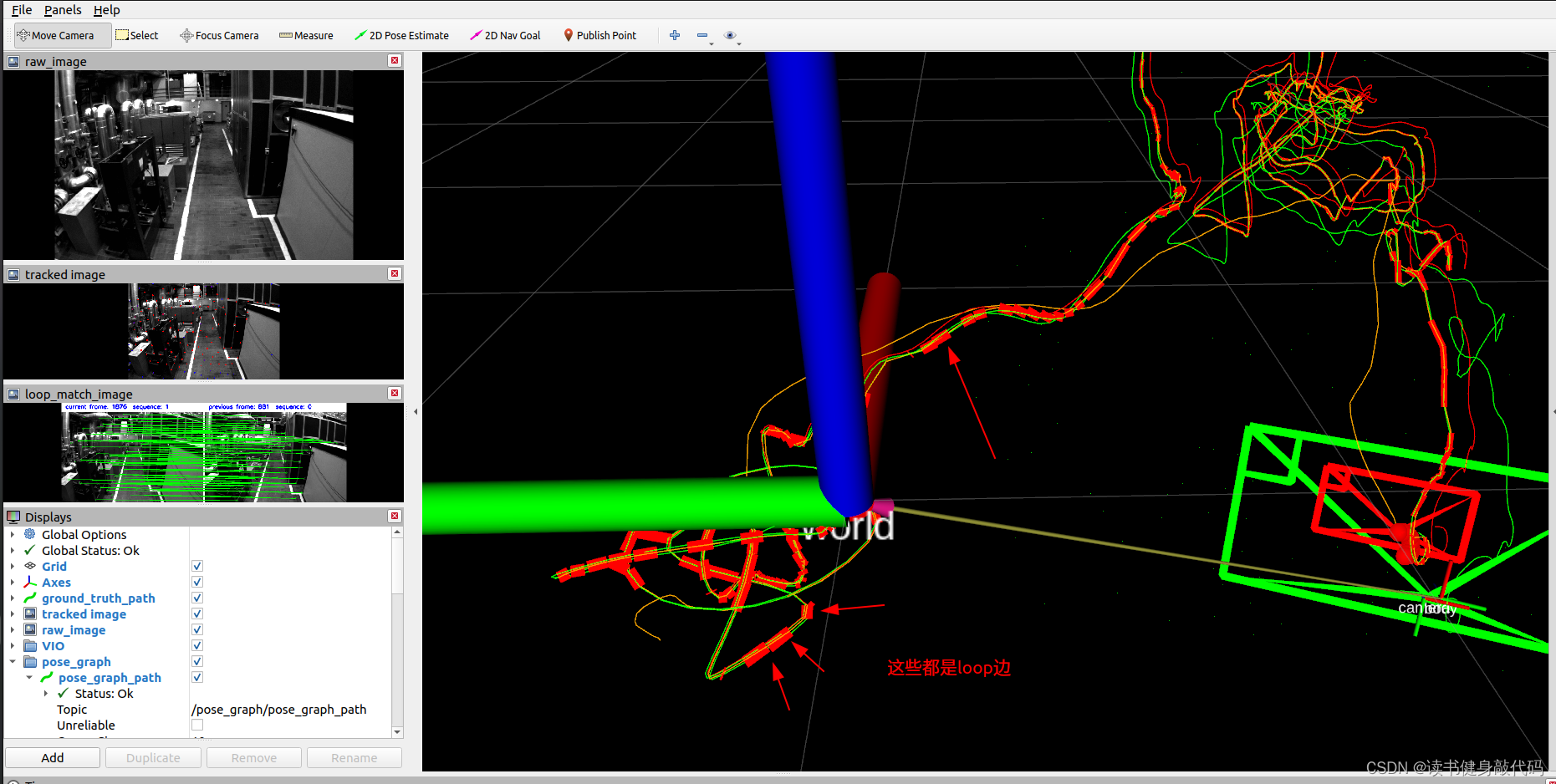
VINS-MONO拓展1----手写后端求解器,LM3种阻尼因子策略,DogLeg,构建Hessian矩阵
文章目录 0. 目标及思路1. 非线性优化求解器2. 基于VINS-MONO的Marginalization框架构建Hessian矩阵2.1 estimator.cpp移植2.2 solve.cpp/preMakeHessian()2.3 solve.cpp/makeHessian() 3. solve.cpp/solveLinearSystem()求解正规方程4. 更新状态5. 迭代求解6. EVO评估结果7. 待…...

RxJS 操作符-学习笔记
提前准备: pipe 方法: 用于组合多个操作符,可以将一系列操作符作为参数传递给 pipe 方法,这些操作符将 依次 对数据流进行处理。这里的依次很关键,也代表着pipe()中组合的这么几个操作符的执行顺序就是从开始一直到结束的,其中的…...

【Linux】linux配置静态IP、动态IP方法汇总
1、systemd-networkd 1.1 说明 systemd-networkd是systemd 的一部分 ,负责 systemd 生态中的网络配置部分(systemd-networkd.service, systemd-resolved.service)。使用 systemd-networkd,你可以为网络设备配置基础的 DHCP/静态IP网络等,还可以配置虚拟网络功能,例如网桥…...

Hive自定义函数支持国密SM4解密
当前项目背景需要使用到国密SM4对加密后的数据进行解密,Hive是不支持的,尝试了华为DWS数仓,华为只支持在DWS中的SM4加密解密,不支持外部加密数据DWS解密 新建Maven工程 只需要将引用的第三方依赖打到jar包中,hadoop和…...
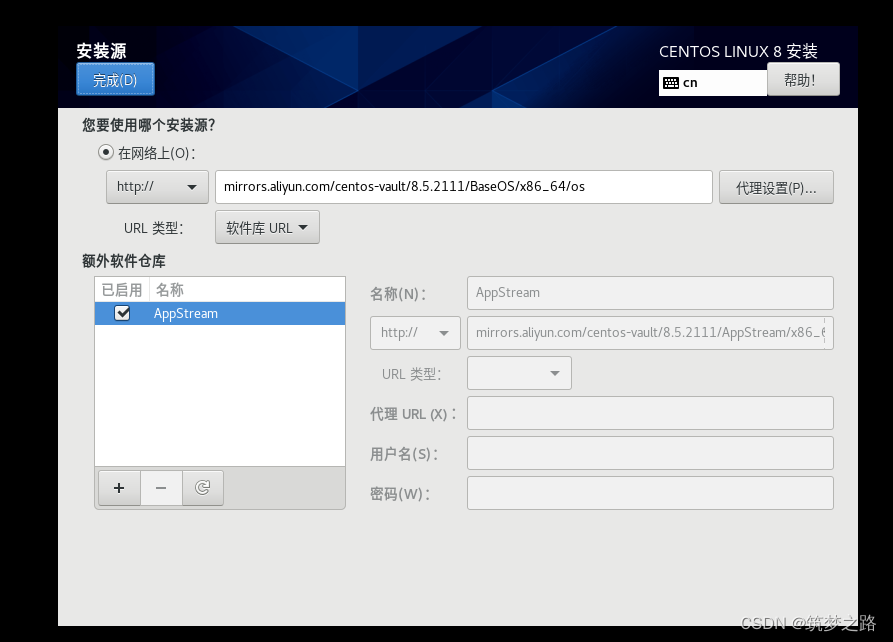
CentOS 8 8.5.2111 网络在线安装系统 —— 筑梦之路
之前写过一篇关于centos 8 官方停止更新维护后解决yum源问题的文章: CentOS 8 停止维护后换可用yum源——筑梦之路_http://ftp.iij.ad.jp/pub/linux/centos-vault/8.5.21-CSDN博客 由于centos 8 dvd的镜像比较大,有时候我们根本不需要去下载一个10G以上…...

安全与认证Week3
目录 Key Management 密钥管理 密钥交换、证书 密钥的类别 密钥管理方面 密钥分发问题 密钥分发方案 混合密钥分发 公钥分发 公钥证书 X.509 理解X.509 X.509证书包含 X.509使用过程 X.509身份验证服务 X.509版本3 取消 由X.509引申关于CA 用户认证、身份管理…...

跟我学c++中级篇——再谈C++20中的协程
一、协程 在前面分析过协程是什么,也对c20中的协程的应用进行了举例说明。所以这次重点分析一下c20中的整体构成及应用的方式。等明白了协程是如何动作的,各种情况下如下何处理相关的事件,那么在以后写协程时就不会死搬硬套了。 二、整体说…...
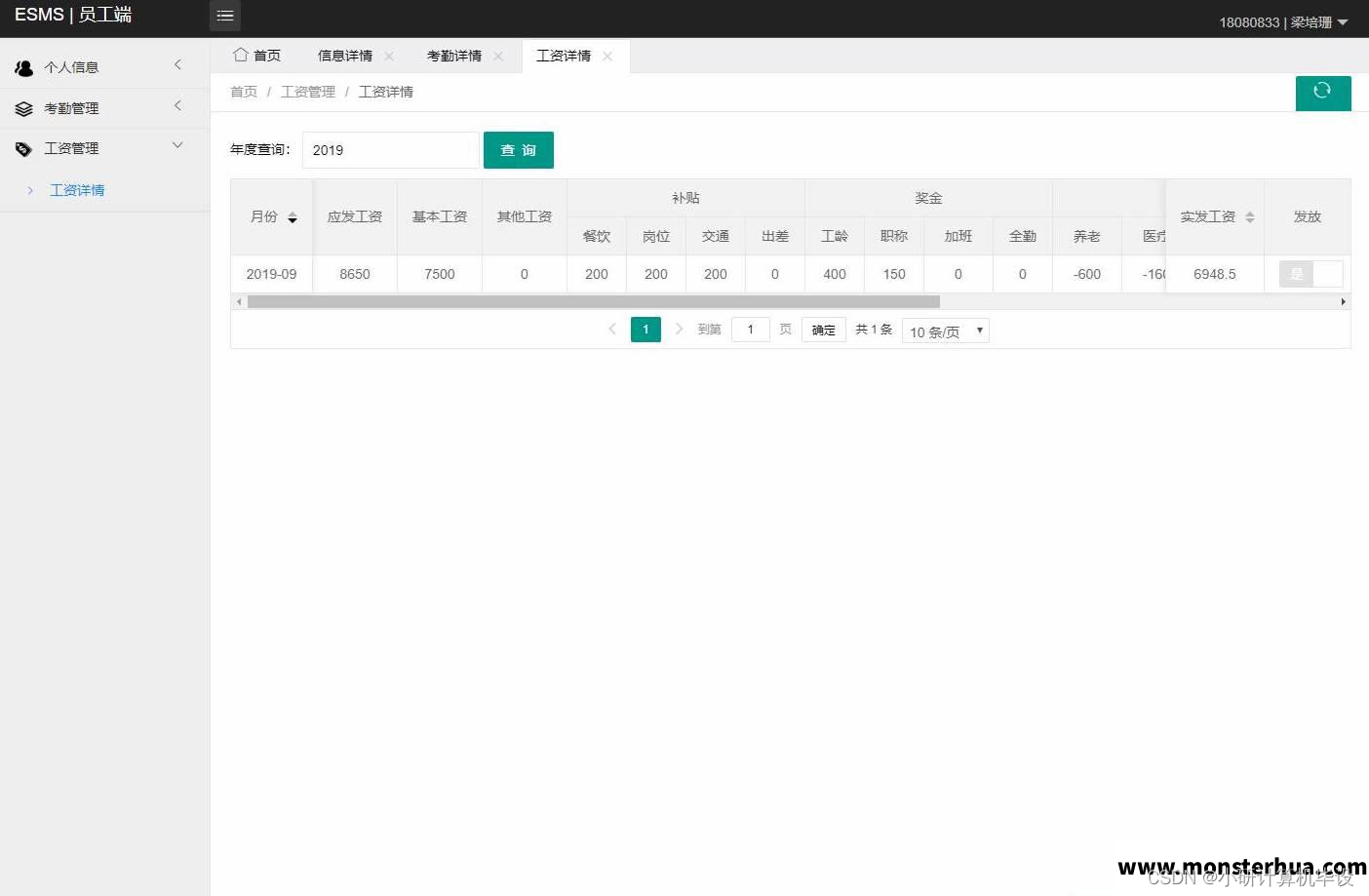
【计算机毕业设计】SSM企业工资管理系统
项目介绍 本项目包含管理员与普通员工两种角色, 管理员角色包含以下功能: 管理员登录,员工管理,部门管理,岗位管理,职称管理,工龄奖金管理,工资项管理,考勤管理,工资查询,统计图表等功能。 员工角色包含以下功能: 员工登录,个人信息管理…...

x-cmd pkg | doggo - 现代化的 DNS 客户端
目录 简介首次用户快速实验指南功能特点类似工具与竞品进一步探索 简介 doggo 是一个由 Karan Sharma 于 2020 年使用 Go 语言开发的 DNS 客户端。它类似于 dig 命令,但旨在以现代化、简洁和可读的格式输出 DNS 查询结果。 首次用户快速实验指南 使用 x doggo 即可…...
c++-智能指针
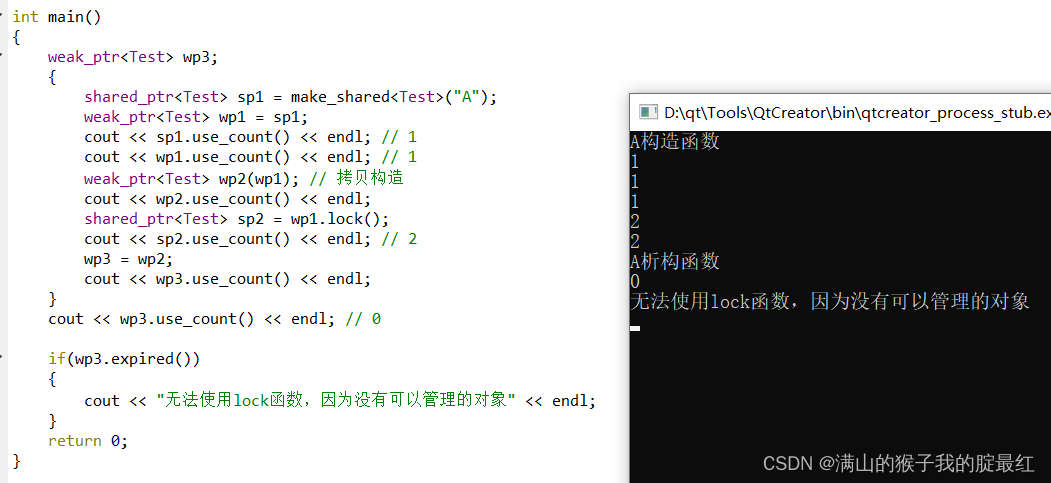
1、概念 堆内存的对象需要手动使用delete销毁,如果忘记使用delete销毁就会造成内存泄漏。 所以C在ISO 98标注中引入了智能指针的概念,并在C11 中趋于完善。 使用智能指针可以让堆内存对象具有栈内存对象的特性。原理时给需要自动回收的堆内存对象套上一层…...
烟花燃放如何管控?智能分析网关V4烟火检测保障烟火安全
一、方案背景 随着元旦佳节的热潮退去,春节也即将来临,在众多传统的中国节日里,烟花与烧纸祭祀都是必不可少的,一方面表达了人们对节日的庆祝的期许,另一方面也是一种对故者思念的寄托。烟花爆竹的燃放不仅存在着巨大的…...

Vue实现版本号输入、删除时光标自动移动到上、下一个输入框前端demo
前言 首先声明,我平时的工作主要是后端JAVA开发,该demo为前端练习,记录一下劳动成果,希望对大家有所帮助,如果有写的不妥的地方,欢迎大家指正,一起学习、共同进步。 背景 手机验证码、银行卡…...

【胖虎的逆向之路】Android自制Https证书实现双向认证
Android自制Https证书实现双向认证 1.基本概念1.1 HTTP1.2 HTTPS1.3 加密方式1.3.1 对称加密1.3.2 非对称加密 1.4 SSL 功能1.4.1 客户对服务器的身份认证1.4.2 服务器对客户的身份认证1.4.3 建立服务器与客户之间安全的数据通道 1.5 CA 证书 2.证书生成2.1 生成根证书…...

解析千兆多模光模块SFP-GE-SX
千兆多模光模块是一种基于光纤通信的光电转换模块,具有千兆(Gigabit)级别的传输速率。本文将对千兆多模光模块的定义、传输距离、参数、及其应用领域等进行详细介绍。 一、千兆多模光模块SFP-GE-SX是什么? 千兆多模光模块SFP-GE-S…...
Go语言基础简单了解
文章目录 前言关于Go学习流程 基础语法注释变量常量数据类型运算符fmt库 流程控制if、switch、selectfor、break、continue遍历String 函数值传递和引用传递deferinit匿名、回调、闭包函数 数组和切片Map结构体自定义数据类型接口协程和channel线程锁异常处理泛型文件读取文件写…...

kafka重平衡经验总结
文章目录 概要背景解决方法技术细节小结 概要 关于kafka重平衡问题在实践工作的应用 背景 重平衡包括以下几种场景: 消费者组内成员发生变更,这个变更包括了增加和减少消费者。注意这里的减少有很大的可能是被动的,就是某个消费者崩溃退出了主题的分…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
