基于python的leetcode算法介绍之动态规划
文章目录
- 零 算法介绍
- 一 例题介绍 使用最小花费爬楼梯
- 问题分析
- Leetcode例题与思路
- [118. 杨辉三角](https://leetcode.cn/problems/pascals-triangle/)
- 解题思路
- 题解
- [53. 最大子数组和](https://leetcode.cn/problems/maximum-subarray/)
- 解题思路
- 题解
- [96. 不同的二叉搜索树](https://leetcode.cn/problems/unique-binary-search-trees/)
- 解题思路
- 题解
- [322. 零钱兑换](https://leetcode.cn/problems/coin-change/)
- 解题思路
- 题解
- [124. 二叉树中的最大路径和](https://leetcode.cn/problems/binary-tree-maximum-path-sum/)
- 解题思路
- 题解
零 算法介绍
动态规划(Dynamic Programming,DP)是一种解决最优化问题的算法思想,通过将问题分解成更小的子问题来解决。其核心思想是将一个问题分解成更小的、相互独立的子问题,然后将子问题的解组合起来,形成原问题的解。但与之前的算法不一样的是,动态规划强调的是动态的过程,即在程序计算时,会出现随程序运行而变化的参数辅助程序完成算法计算。
动态规划算法的主要特点包括:
-
重叠子问题:动态规划算法解决的问题通常包含许多重叠的子问题。
-
状态转移方程:动态规划算法通常使用状态转移方程来描述问题的状态和状态转移关系。
-
自底向上:动态规划算法通常采用自底向上的方法,即从最小的子问题开始解决,逐步解决更大的子问题。
动态规划算法的应用范围非常广泛,包括:
-
组合优化问题:如背包问题、旅行商问题等。
-
序列问题:如最长公共子序列、最长递增子序列等。
-
图论问题:如最短路径问题、最小生成树问题等。
-
动态规划在游戏、人工智能、计算机图形学等领域也有广泛应用。
动态规划算法有很多变种,如线性动态规划、树形动态规划、网格动态规划等。在实际应用中,需要根据问题的特点选择合适的动态规划算法。
一 例题介绍 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
问题分析
动态规划强调的是动态的过程, 故当我们再看这道题目的时候,我们的关注点是 一旦你支付此费用,即可选择向上爬一个或者两个台阶。 当我们转换一下思路,则是:当前台阶的价值应该是由前一个台阶或是前前一个台阶决定的。如果这套规则适用的话,则代表第N阶的台阶等于total[n] = min(total[n-1]+cost[n-1], total[n-2]+cost[n-2])。即,当前台阶的最低花费应该是在上两级台阶的最小开销中进行选择。
代码呈现如下:
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:old1, old2 = 0, 0 # 初始化前前一个台阶和前一个台阶的初始价格for i in cost: # 对所有台阶遍历temp = i + min(old1, old2) # 第N个台阶的花费是当前第N个台阶的价格加上前两级台阶中小的那个old1, old2 = old2, temp # 迭代return min(old1, old2)
Leetcode例题与思路
接下来,我们列举关于Leetcode的几道例题,并通过动态规划的方式进行求解:
118. 杨辉三角
给定一个非负整数 *numRows,*生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
11 11 2 11 3 3 11 4 6 4 1
解题思路
这道题目是最简单的动态规划题目,对于第N行来说,其第1个和最后一个应当为1,其余位置可以通过上一行中当前位置和当前位置的下一位置两个元素求和完成。转换成代码如下所示:
题解
class Solution:def generate(self, numRows: int) -> List[List[int]]:res = []for i in range(numRows):row = [None for _ in range(i + 1)]row[0], row[-1] = 1, 1for j in range(1, len(row) - 1):row[j] = res[i - 1][j - 1] + res[i - 1][j]res.append(row)return res
53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
解题思路
由于这边仅需要找到最大和,无需判断位置。故我们仅需判断最大值作为我们的判断。那么最大子数组和应该有什么特点呢?其实从这道题目中我们就会发现从哪开始到哪结束是不重要的。需要关注的是在第N个元素的位置,我们之前的元素和大于零还是小于零。什么意思呢?即之前元素之和如果小于0,那么对于后续元素求和只有负面效果,故可以直接丢弃从第N个元素开始重新统计。而我们只需要在这个过程中,找到累计和最大的值就可以了。由题目的提示可知,-10^4 <= nums[i] <= 10^4。故我们可以选择-10000作为初始化:
题解
class Solution:def maxSubArray(self, nums: List[int]) -> int:temp, max_value = -10000, -10000for i in nums:temp = max(temp + i, i)max_value = max(temp, max_value)return max_value
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
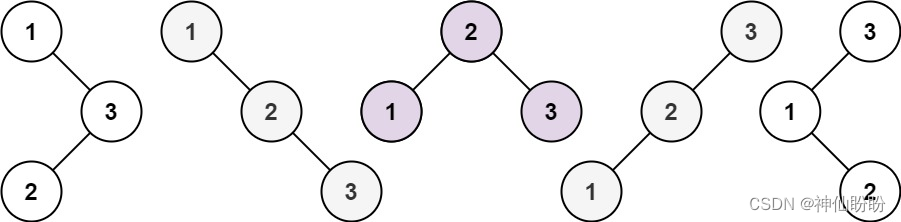
解题思路
首先我们需要明确一个概念,什么是二叉搜索树:
二叉搜索树(Binary Search Tree, BST)是一种特殊的二叉树,它的每个节点都有一个关键值,并且所有节点的关键值满足以下性质:
-
节点的左子树(如果存在)的关键值都小于节点的关键值。
-
节点的右子树(如果存在)的关键值都大于节点的关键值。
-
节点的左右子树(如果存在)也都是二叉搜索树。
这种结构使得二叉搜索树在查找、插入和删除操作方面具有较高的效率。
那么面对这样一道题,我们该如何求解呢?首先,我们需要明确一个问题,就是对于N个节点的二叉树,我们可以把这个二叉树从节点切分,分为成小于该长度的二叉树来求解。换句话说,我们在面对一个4节点的二叉搜索树,可以看作013[代表左子树0,根节点1,右节点3],112, 211 , 310。所以我们仅需要得到1节点,2节点和3节点的树就可以推出4节点的数量。那么我们可以快速推出,0节点仅存在1种排列,1节点仅存在1种排列。从2节点开始,我们可以通过公式进行推理:N节点的树可以看作N个根和他们的左右子树。故,我们可以通过左子树的种类乘以右子树的种类得到每个节点存在子树的个数。继续以4节点树为例,可以分为013,112, 211 , 310。当我们知道0,1,2,3个节点的数量时,就可以得到013[1*5],112[1*2], 211[2*1] , 310[5*1]。故四节点可以构建5+2+2+5=14个排列。
题解
class Solution:def numTrees(self, n: int) -> int:node_list = [1 for i in range(0, n+1)]for i in range(2, n+1):node_list[i] = sum([node_list[j] * node_list[i-j-1] for j in range(i)])return node_list[-1]
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
解题思路
这道题目可以转换成走楼梯的思路。如果还不能get到这个思路的话,我们再细说一下:
针对N块钱,凑出来的方法必然是考虑N块钱前一步的状态,即N块钱减去coins的状态下需要多少步。所以我们从coins最小的储蓄开始执行,通过对比上一步的所有状态,选择其中需要部署最小的作为自己的结果,一直到amount,得到最终结果。
题解
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:answer = [-1 for i in range(amount+1)] # 初始化所有状态answer[0] = 0 # 初始化0,这样coins中的所有元素的步长都为1for i in range(min(coins), amount+1): # 计算到amount的步长mins = 2**31for j in coins: # 对比coins中的所有状态if i - j >= 0 and answer[i - j] > -1: # 当上一状态合法且存在时,获得最小步数mins = min(answer[i - j] + 1, mins)answer[i] = mins if mins != 2**31 else -1 # 更新当前状态return answer[-1]
124. 二叉树中的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
解题思路
这是一道将动态规划运用到树上的一道题,结合了树的搜索,故还需要用到递归的方法进行搜索。
我们对其中任意节点进行思考,如何判断当前节点以下的树节点应当被省略?即会降低全局解的情况,也就是当前节点联通的路径小于0的情况下。那怎么得到当前节点的联通路径呢?即根节点和左子树与右子树中较大的值的和。故我们需要注意,**左子树和右子树的返回结果是必然大于0的,否则就没有链接的必要。**那如果不回调的话,最大联通树应该是当前节点加上左节点加上右节点的值,如果当前值大于已知的最大值,那么就可以替换当前的最大值。
题解
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def maxPathSum(self, root: Optional[TreeNode]) -> int:self.answer = -1000self.maxroot(root)return self.answerdef maxroot(self, root):if root == None:return 0else:left = self.maxroot(root.left)right = self.maxroot(root.right)self.answer = max(self.answer, root.val + left + right)return max(max(left, right) + root.val, 0)
以上就是最基础的动态规划,动态规划的题目难度非常大,后续有精力会详细拆开,深入剖析。
相关文章:

基于python的leetcode算法介绍之动态规划
文章目录 零 算法介绍一 例题介绍 使用最小花费爬楼梯问题分析 Leetcode例题与思路[118. 杨辉三角](https://leetcode.cn/problems/pascals-triangle/)解题思路题解 [53. 最大子数组和](https://leetcode.cn/problems/maximum-subarray/)解题思路题解 [96. 不同的二叉搜索树](h…...

通信原理期末复习——计算大题(一)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:V…...
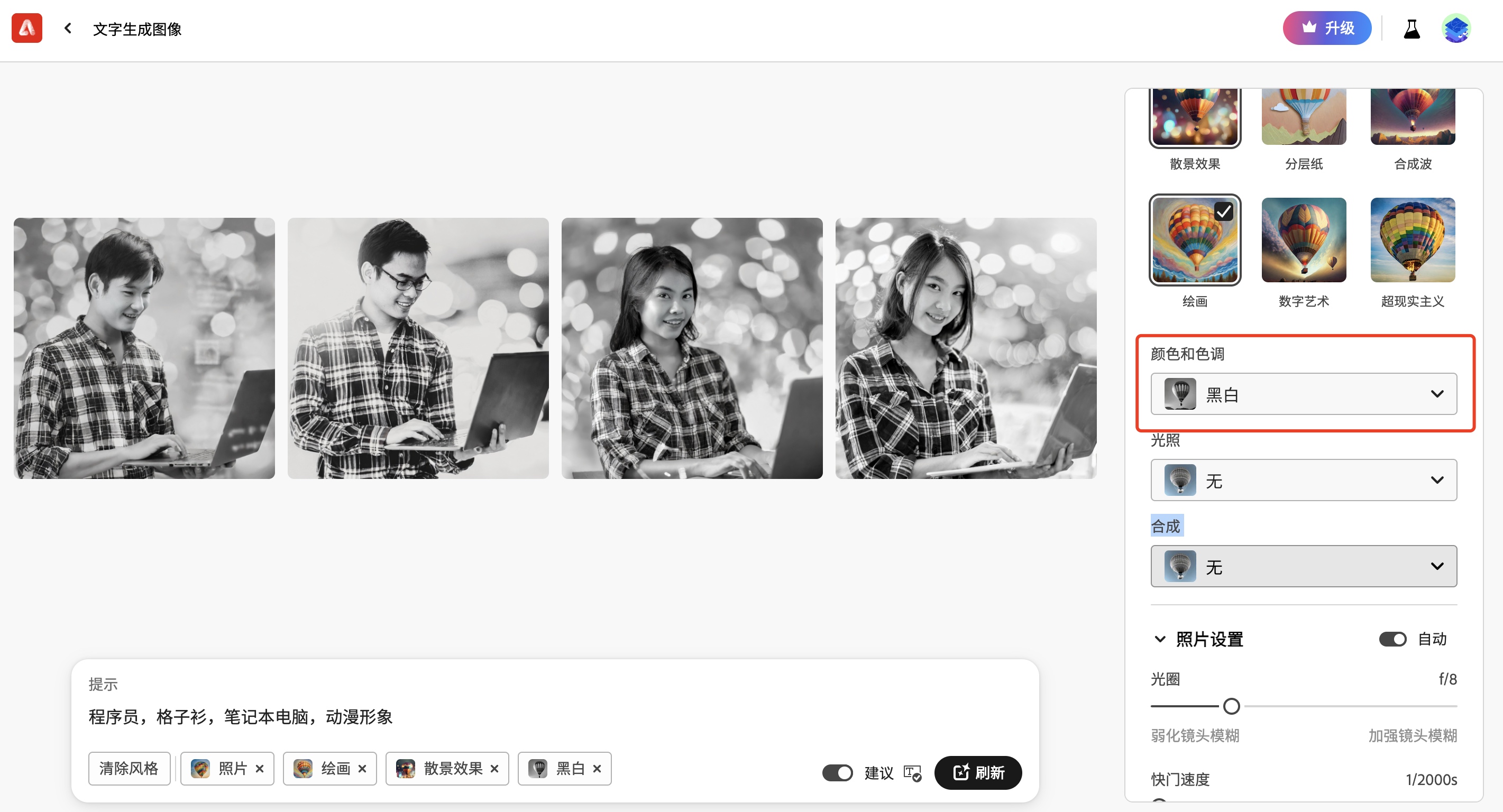
【萤火虫系列教程】2/5-Adobe Firefly 文字生成图像
文字生成图像 登录账号后,在主页点击文字生成图像的【生成】按钮,进入到文字生成图像 查看图像 在文字生成图像页面,可以看到别人生成的图像。 点击某个图像,就可以进入图像详情,可以看到文字描述。 生成图像 我…...

JDK 11:崭新特性解析
JDK 11:崭新特性解析 JDK 11:崭新特性解析1. HTTP Client(标准化)示例代码 2. 局部变量类型推断的扩展示例代码 3. 新的字符串方法示例代码 4. 动态类文件常量示例代码 5. Epsilon 垃圾收集器使用方式 结语 JDK 11:崭新…...

leetcode.在链表中插入最大公约数
文章目录 题目解题方法复杂度Code Problem: 2807. 在链表中插入最大公约数 题目 给你一个链表的头 head ,每个结点包含一个整数值。 在相邻结点之间,请你插入一个新的结点,结点值为这两个相邻结点值的 最大公约数 。 请你返回插入之后的链表。…...
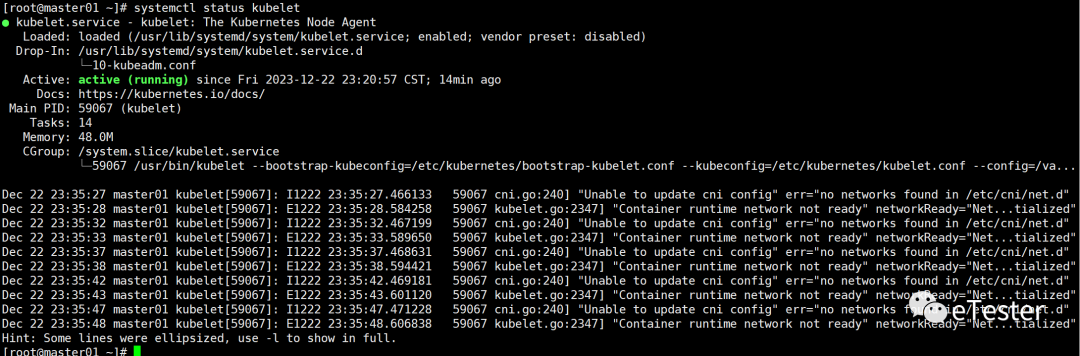
云原生学习系列之基础环境准备(单节点安装kubernetes)
一、环境要求 操作系统CentOS 7.x-86_x64 硬件配置:内存2GB或2G,CPU 2核或CPU 2核,需要在虚拟机中提前设置好,不然后续会报错 二、系统初始化 1、设置主机名 # 在master节点执行 hostnamectl set-hostname master01 2、配置主…...
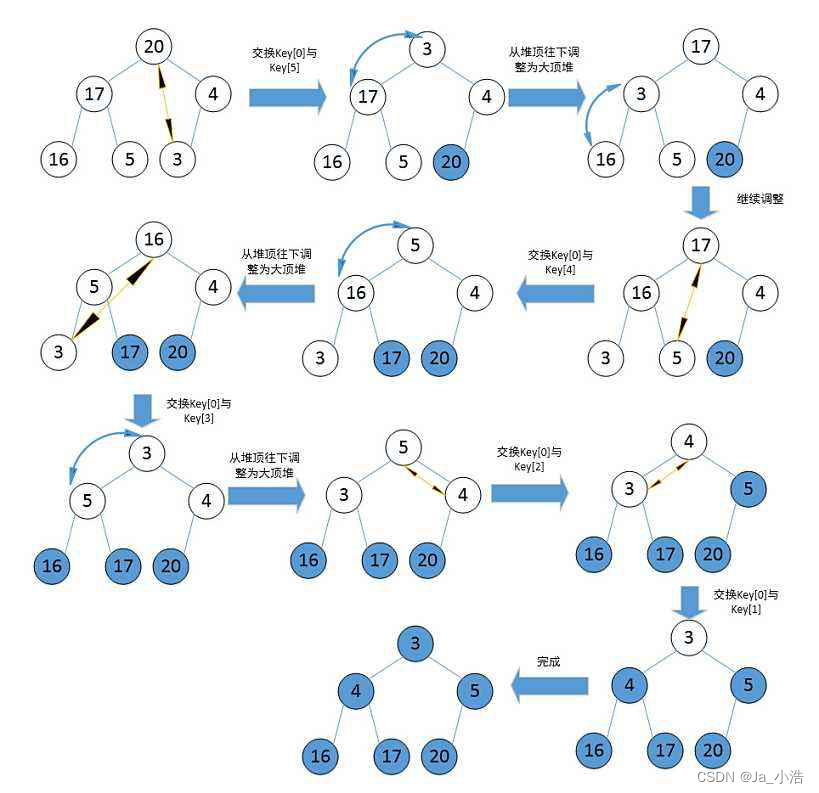
【数据结构】二叉树的概念及堆
前言 我们已经学过了顺序表、链表、栈和队列这些属于线性结构的数据结构,那么下面我们就要学习我们第一个非线性结构,非线性结构又有哪些值得我们使用的呢?那么接下来我们就将谈谈树的概念了。 1.树的概念与结构 1.1树的概念 树是一种非线性…...
美年大健康黄伟:从选型到迁移,一个月升级核心数据库
核心生产系统的数据库,从接到替换需求到完成分布式升级,需要多久?一个月,这是美年大健康的回答。一个月集中调配各种资源,美年大健康完成了应用程序基本零改造的平滑迁移,新数据库在成本更低的前提下&#…...

OpenHarmony应用构建工具Hvigor的构建流程
前言 OpenHarmony 应用和服务使用 Hvigor 作为工程的构建工具。本篇文章将介绍 Hvigor 的构建流程,通过修改脚本配置使 Hvigor 执行自定义任务。 Hvigor 的构建流程 加载命令行参数和环境变量;初始化项目结构,创建 Project 和 Module 实例…...

ChatGPT在金融财务领域的10种应用方法
1.生成报告 在金融领域中,最耗时的任务之一是报告生成。通过ChatGPT,您可以在一定程度上自动化这个过程。这款人工智能工具可以获取关于公司财务表现的结构化数据,并生成一份书面摘要,详细说明关键点、趋势和观察结果。这个功能在…...
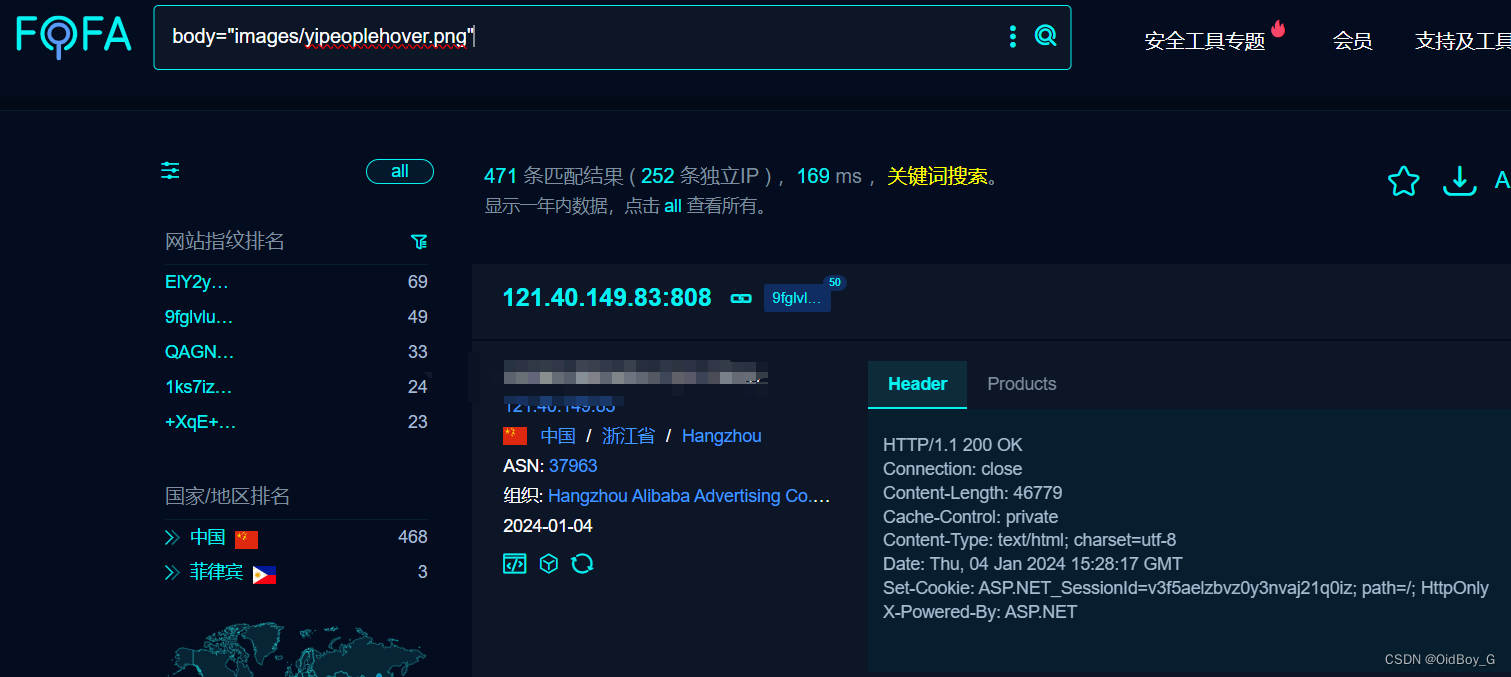
全程云OA ajax.ashx SQL注入漏洞复现
0x01 产品简介 全程云OA为企业提供日常办公管理、公文管理、工作请示、汇报、档案、知识体系、预算控制等26个功能,超过100多个子模块。为企业内部提供高效、畅通的信息渠道,同时也能大力推动公司信息系统发展,提高企业的办公自动化程度和综合管理水平,加快企业信息的流通…...
VMware 安装 macOS虚拟机(附工具包)
VMware 安装 macOS虚拟机,在Windows上体验苹果macOS系统! 安装教程:VMware 安装 macOS虚拟机VMware Workstation Pro 是一款强大的虚拟机软件,可让您在 Windows 电脑上运行 macOS 系统。只需简单几步操作,即可轻松安装…...

Tomcat与Servlet是什么关系
Tomcat与Servlet是什么关系 Apache Tomcat和Servlet之间存在密切的关系,可以说它们是一对密切合作的组件。下面是它们的关系: Tomcat是Servlet容器: Tomcat是一个开源的、轻量级的Servlet容器。Servlet容器是一个Web服务器扩展,用…...

C++11_右值引用
文章目录 前言一、右值引用是什么?那么,什么又是右值?右值引用 二、使用步骤和意义1.1.11.2 2.右值引用的最大意义2.1 完美转发2.2 万能折叠 前言 C11 是2011年对C这门语言发布的新标准,并且此次标准引入了十分多的新特性&#x…...
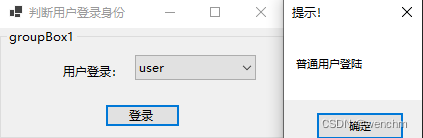
C#使用条件语句判断用户登录身份
目录 一、示例 二、生成 利用条件语句判断用户登录身份,根据用户登录身份的不同,给予相应的操作权限。 一、示例 主要用if语句及ComboBox控件。其中,ComboBox是窗体中的下拉列表控件,在使用ComboBox控件前,可以先向…...

在VM下使用Composer完成快照方式的软件制作
Composer允许您构建软件、应用程序、偏好设置文件或是文档的安装包,安装包可以部署到远程电脑或是作为镜像流程的一部分。构建软件包的第一步就是创建包源,根据要打包的软件,Composer允许您监视软件的安装和使用驱动器上已存在的文件来创建包…...
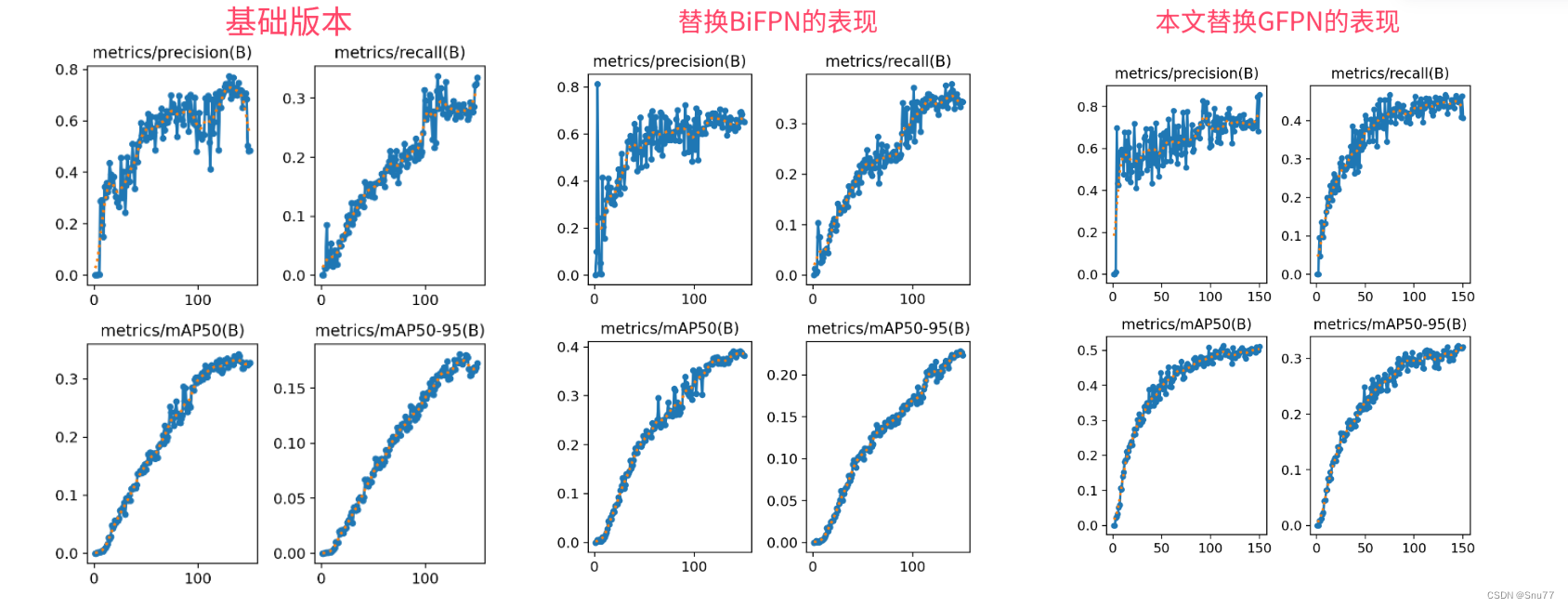
YOLOv5改进 | Neck篇 | 利用Damo-YOLO的RepGFPN改进特征融合层
一、本文介绍 本文给大家带来的改进机制是Damo-YOLO的RepGFPN(重参数化泛化特征金字塔网络),利用其优化YOLOv5的Neck部分,可以在不影响计算量的同时大幅度涨点(亲测在小目标和大目标检测的数据集上效果均表现良好涨点幅度超级高!)。RepGFPN不同于以往提出的改进模块,其…...
设计模式——最全梳理,最好理解
新年献礼! 设计模式呕心梳理 创建型模式 单例模式(Singleton Pattern)https://blog.csdn.net/qq_34869143/article/details/134874044 整理中... 结构型模式 代理模式(Proxy Pattern)https://blog.csdn.net/qq_34…...
外包干了4个月,技术退步明显了...
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四…...
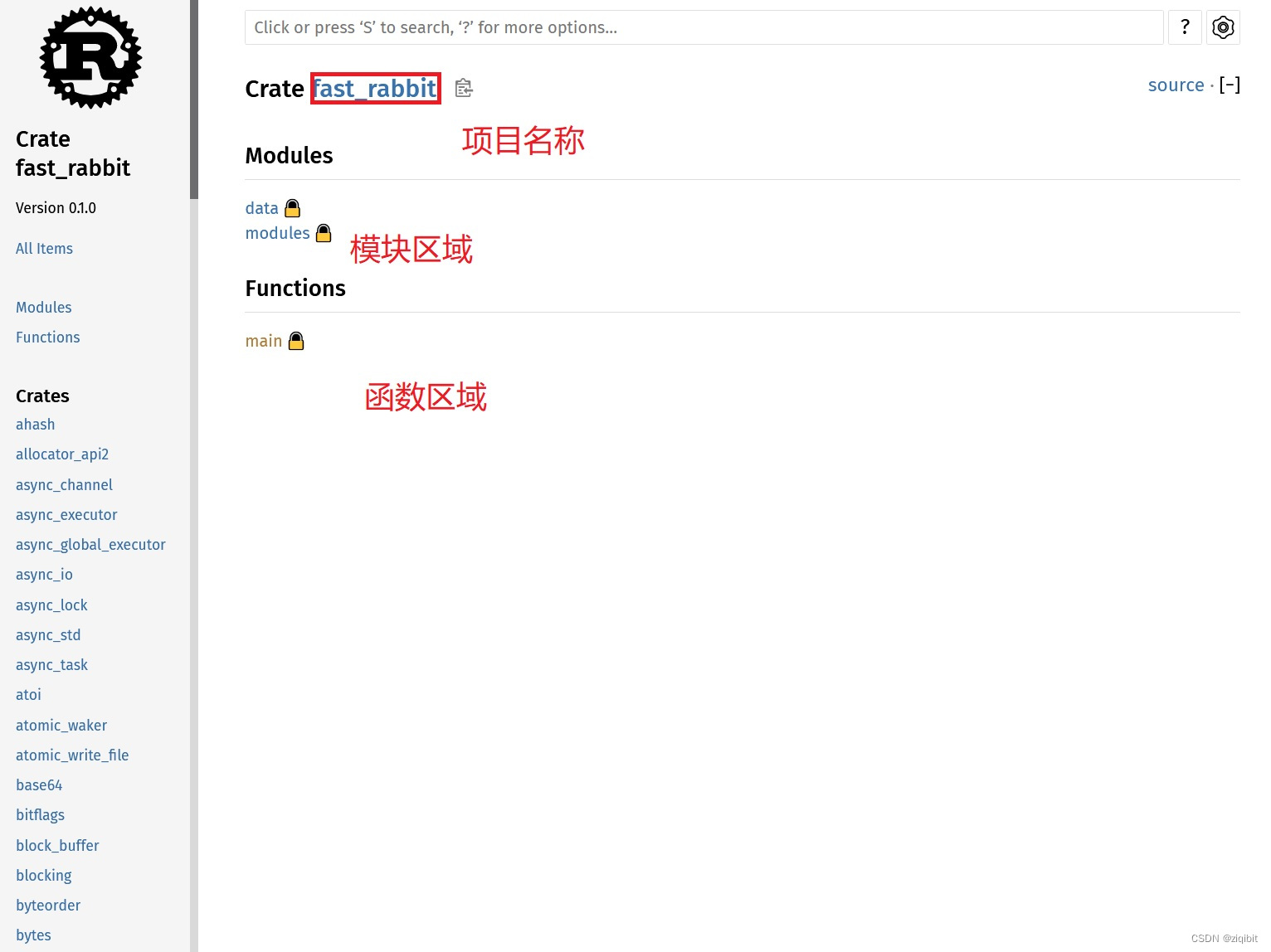
rust 注释文档生成 cargo doc
rust的cargo文档生成 只需要在每个函数写清楚注释,就可以自动生成文档,很方便 即不用写文档,又可以快速查看,是开发rust的必备技能 rust安装和开发环境配置,可以参考:链接 1.写注释的方法 连续三个 \ 即…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
