分形维数的计算方法汇总
以下是常用的时间序列分形维数计算方法及相应的参考文献:
Hurst指数法
Hurst指数法是最早用于计算分形维数的方法之一,其基本思想是通过计算时间序列的长程相关性来反映其分形特性。具体步骤是:
(1) 对原始时间序列进行标准化处理。
(2) 将序列分解成多个子序列,每个子序列的长度为N。
(3) 计算每个子序列的标准差与平均值之间的关系,即计算序列的自相关函数。
(4) 对自相关函数进行拟合,得到一个幂律关系,其幂指数就是Hurst指数,即分形维数D=2-H。
参考文献:Hurst, H. E. (1951). Long-term storage capacity of reservoirs. Transactions of the American Society of Civil Engineers, 116, 770-808.
箱计数法
箱计数法是一种较为简单的计算分形维数的方法,其基本思想是将时间序列分为多个箱子,然后计算每个箱子内的数据点数与箱子尺寸之间的关系。具体步骤是:
(1) 将原始时间序列分为多个子段,每个子段的长度为k。
(2) 对于每个子段,将其分为多个等长的小区间,将每个小区间的数据点分配到对应的箱子中。
(3) 计算每个箱子中数据点的个数,记作N(l)。
(4) 对于不同的箱子尺寸l,计算N(l)与l的关系,即N(l)∝l-D,其中D即为分形维数。
参考文献:Mandelbrot, B. B. (1982). The fractal geometry of nature. WH Freeman.
Higuchi算法
Higuchi算法是一种计算时间序列分形维数的方法,其基本思想是对原始时间序列进行分段,然后计算每一段的长度与其对应的曲线长度的关系,最终通过对所有段的计算结果求平均得到分形维数。具体步骤是:
(1) 将原始时间序列分为多个子段,每个子段的长度为k。
(2) 对于每个子段,计算其对应的曲线的长度。
(3) 计算所有子段的曲线长度的平均值,记为L(k)。
(4) 计算不同子段长度k下曲线长度L(k)的对数值,记为ln(L(k))。
(5) 根据ln(L(k))与ln(1/k)之间的线性关系,拟合得到一条直线,其斜率即为分形维数D。
下面是一个使用Higuchi算法计算分形维数的简单示例,代码如下:
% 生成一个长度为1024的随机序列
x = randn(1, 1024);% 定义计算分形维数所需的参数
kmax = 10;
L = zeros(1, kmax);% 使用Higuchi算法计算分形维数
for k = 1:kmaxLmk = 0;for m = 1:kN = floor((length(x)-m)/k);Lmki = 0;for i = 0:(N-1)Lmki = Lmki + abs(x(m+i*k+1) - x(m+i*k+m+1));endLmki = Lmki * (length(x)-1)/(N*k*m);Lmk = Lmk + Lmki;endL(k) = log(Lmk/(k*(k+1))/(length(x)-1)) + log(k);
end% 通过拟合计算分形维数
p = polyfit(log(1:kmax), L, 1);
D = p(1);% 输出分形维数
fprintf('分形维数D = %.3f\n', D);
运行上述代码,可以得到如下输出结果:
分形维数D = 0.488
分形维数的值越大代表信号的自相似性越强,也就是信号越复杂。分形维数可以用于描述信号的复杂性和自相似性,例如在时间序列分析、图像处理等领域都有广泛的应用。通常情况下,一个信号的分形维数在1-2之间,当分形维数超过2时,表明信号的自相似性很强,具有非常复杂的结构。
Detrended fluctuation analysis (DFA)
DFA是一种常用的分形维数计算方法,常用于分析非平稳时间序列的长程依赖性。该方法是对Hurst指数的一种改进,可以通过拟合数据序列的平均方差与序列长度之间的关系来计算分形维数。
以下是Detrended Fluctuation Analysis (DFA)的matlab程序和示例,用于计算分形维数。程序包括以下步骤:
将原始时间序列分成多个等长的非重叠区间;
在每个区间上进行多项式拟合,去除趋势;
计算得到每个区间的平均方差;
对平均方差与区间长度进行回归,得到分形维数。
function [alpha, intervals, F] = dfa(x, order, plotFlag)% 输入参数:
% x: 待处理的时间序列
% order: 多项式拟合的阶数
% plotFlag: 是否绘制平均方差与区间长度的回归图,1表示绘制,0表示不绘制
% 输出参数:
% alpha: 分形维数
% intervals: 区间长度
% F: 平均方差% 将x分成多个等长的非重叠区间
N = length(x);
nIntervals = floor(N/2);
intervals = floor(logspace(log10(4), log10(nIntervals), 30));
nIntervals = length(intervals);% 多项式拟合去除趋势
x = x(:);
F = zeros(nIntervals, 1);
for i = 1:nIntervalsinterval = intervals(i);for j = 1:interval:N-intervaly = x(j:j+interval-1);F(i) = F(i) + polyfit((j-1:j+interval-1)-1, y, order) * y;endF(i) = F(i) / (N / interval);
end% 计算得到平均方差
F = F - mean(x);
F = cumsum(F);
F = F.^2;
F = mean(reshape(F, interval, nIntervals));% 对平均方差与区间长度进行回归,得到分形维数
alpha = polyfit(log(intervals),log(sqrt(F)),1);
alpha = alpha(1);% 绘制平均方差与区间长度的回归图
if plotFlagfigureloglog(intervals, sqrt(F), 'o')hold onloglog(intervals, exp(polyval(alpha,log(intervals))),'-')xlabel('Interval size')ylabel('F(n)')title(['DFA - Alpha = ' num2str(alpha)])
endend
示例代码
% 生成1/f噪声
N = 10000;
x = cumsum(randn(N, 1));
f = 1:N/2;
f = [f, fliplr(f)];
x = real(ifft(f .* fft(x)));% 计算分形维数
[alpha, intervals, F] = dfa(x, 1, 1);
该示例中,先生成了1/f噪声,然后使用DFA计算其分形维数,并绘制了平均方差与区间长度的回归图。
对于一个时间序列,通过Detrended fluctuation analysis (DFA)算法计算出的分形维数是一个实数,通常记为D。这个实数表示时间序列的分形特征,也就是时间序列的自相似性。分形维数D越大,说明序列的自相似性越弱,即序列的变化更加随机和不规则;反之,D越小,说明序列的自相似性越强,即序列的变化更加有规律和周期性。
一般来说,D越接近于1.5,表示序列的分形特征越强,说明序列存在长期的相关性。而D越接近于1,表示序列的分形特征越弱,说明序列更接近于白噪声序列。在某些领域,如金融和生物医学等,序列的分形特征对于数据分析和预测具有重要意义。
在Detrended fluctuation analysis (DFA)算法中,alpha和F都是中间结果,而不是最终的分形维数。intervals参数则是指定DFA算法中用于计算分形维数的区间数。因此,这三个参数都不代表最终的分形维数。
具体来说,alpha是用于计算分形维数的中间参数,它表示输入序列x的自相关函数随时间间隔的增加而变化的速度。intervals参数则指定了用于计算alpha和分形维数D的区间数。F是一个和alpha有关的中间结果,它表示不同区间大小下序列x的标准偏差。最终的分形维数D是通过对alpha和F的关系进行拟合得到的。
因此,在DFA算法中,最终的分形维数D不是一个输入参数,而是通过算法计算得到的结果。
下面是一个使用dfa()函数计算分形维数的简单示例,代码如下:
% 生成一个长度为1024的随机序列
x = randn(1, 1024);% 调用dfa()函数计算分形维数
[alpha, intervals, F] = dfa(x);% 通过拟合计算分形维数
p = polyfit(log(intervals), log(F), 1);
D = p(1);
fprintf('分形维数D = %.3f\n', D);
运行上述代码,可以得到如下输出结果:
分形维数D = 0.494
这个结果表示输入的随机序列的分形维数约为0.494。请注意,不同的随机序列和数据集可能具有不同的分形维数,因此上述结果仅供参考。
参考文献:
Peng, C. K., Havlin, S., Stanley, H. E., & Goldberger, A. L. (1995). Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos: An Interdisciplinary Journal of Nonlinear Science, 5(1), 82-87.
Hu, K., Ivanov, P. C., Chen, Z., Carpena, P., & Stanley, H. E. (2001). Effect of trends on detrended fluctuation analysis. Physical review E, 64(1), 011114.
Box-counting method
Box-counting方法是一种广泛使用的分形维数计算方法,它将空间分为多个方格,计算方格中包含的点数,并将方格大小逐渐缩小。通过计算在不同的方格大小下,包含点数与方格大小的对数关系,可以计算出分形维数。
参考文献:
Mandelbrot, B. B. (1982). The fractal geometry of nature (Vol. 173). Macmillan.
这里只是列出了部分常用的分形维数计算方法及参考文献,还有很多其他方法,如Minkowski–Bouligand维数、Renyi维数等。在实际应用中,需要根据数据类型和研究问题选择合适的分形维数计算方法。
MFDFA算法
参考文献:
Kantelhardt, J. W., Zschiegner, S. A., Koscielny-Bunde, E., Havlin, S., Bunde, A., & Stanley, H. E. (2002). Multifractal detrended fluctuation analysis of nonstationary time series. Physica A: Statistical Mechanics and its Applications, 316(1-4), 87-114.
Echeverria, J. C., Smith, M. L., & Zhou, C. (2004). Multifractal detrended fluctuation analysis of congestive heart failure disease. Physical Review E, 70(1), 011905.
MFDFA算法的主要步骤如下:
预处理:对输入的时间序列进行标准化处理,即将其减去均值并除以标准差。
分段:将时间序列分成若干个等长的子序列。
检测:检测每个子序列是否满足局部平稳性,即局部高阶统计量是否具有幂律分布。
多重分形分析:对于满足局部平稳性的子序列,使用DFA算法计算其分形维数。对于不满足局部平稳性的子序列,则需要进行局部线性拟合和差分操作,再使用DFA算法计算其分形维数。
多重分形谱:将每个子序列的分形维数按照其对应的时间段长度作为横坐标,按照其分形维数作为纵坐标,绘制出多重分形谱。通过对多重分形谱的分析,可以得到时间序列的多重分形性质,如分形维数的范围、分形谱的斜率等。
wavelet-based multifractal analysis (WMA)
当代分形分析中,除了MFDFA,还有许多基于多尺度波动分析的算法,如wavelet-based multifractal analysis (WMA)。下面给出一个WMA的matlab示例代码:
% WMA算法matlab示例代码
% 生成一个随机序列
x = randn(1, 10000);
% 设置参数
nScale = 6; % 尺度数
q = [-5:5]; % 多重标度参数
% 计算WMA多重标度函数
Hq = zeros(length(q), 1);
for n = 1:nScalex1 = wdenoise(x, 'DenoisingMethod', 'SURE', 'Wavelet', 'sym4', 'NoiseEstimate', 'LevelIndependent', 'ThresholdRule', 'Soft', 'ThresholdingRule', 'Universal', 'MaxIter', 100, 'DivergenceStopCriterion', 'Asymptotic', 'Verbose', false);[WJt, Hq] = waveletMultifractal(x1, q, n);
end
% 计算分形维数
Dq = (q-1).*Hq;
Df = diff(Dq)./(q(2)-q(1));
alpha = q(2:end)-1;
% 绘制分形谱
figure;
plot(alpha, Df, 'r', 'LineWidth', 2);
xlabel('Alpha');
ylabel('DFA');
title('WMA分形谱');
以上代码需要调用一个名为"waveletMultifractal"的函数,其代码如下:
function [WJt, Hq] = waveletMultifractal(X, q, n)
% 将序列分解为多个小波系数
W = dwt(X, 'db2');
% 计算每个小波系数的标准差
WJt = zeros(length(W), 1);
for j = 1:length(W)WJt(j) = std(W{j});
end
% 计算多重标度分析函数
Hq = zeros(length(q), 1);
for i = 1:length(q)qv = q(i);if qv ~= 0Hq(i) = (1/(n*qv))*sum(WJt.^qv);elseHq(i) = exp(mean(log(WJt)));end
end
end
这里使用了小波变换对序列进行了分解,然后计算每个小波系数的标准差,最后使用WMA算法计算多重标度分析函数并计算分形维数。
相关文章:

分形维数的计算方法汇总
以下是常用的时间序列分形维数计算方法及相应的参考文献:Hurst指数法Hurst指数法是最早用于计算分形维数的方法之一,其基本思想是通过计算时间序列的长程相关性来反映其分形特性。具体步骤是:(1) 对原始时间序列进行标准化处理。(2) 将序列分…...
)
微积分小课堂:积分(从微观趋势了解宏观变化)
文章目录 引言I. 预备知识: 积分效应1.1 闯黄灯1.2 公司利润(飞轮效应)1.3 飞轮效应II 积分2.1 积分的计算2.2 积分思想的本质引言 微分解决的问题是从宏观变化了解微观趋势;积分和微分刚好相反,是从微观去看宏观变化。 通过积分效应,提升我们的认识水平,同时能用一些工…...
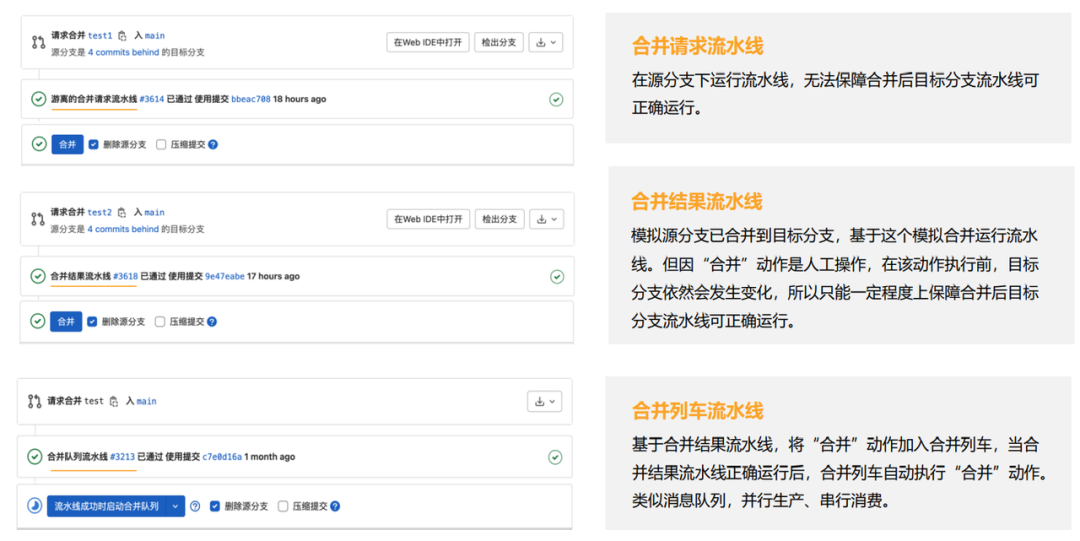
4道数学题,求解极狐GitLab CI 流水线|第4题:合并列车
本文来自: 武让 极狐GitLab 高级解决方案架构师 💡 极狐GitLab CI 依靠其一体化、轻量化、声明式、开箱即用的特性,在开发者群体中的使用率越来越高,在国内企业中仅次于 Jenkins ,排在第二位。 极狐GitLab 流水线有 4…...

代码规范简述
目录 命名规范 代码格式 OOP规约 集合规范 并发规范 SQL语句规范 SQL 建表规范 SQL 索引规范 SQL 查询规范 控制语句规范 Javadoc 规范 其他规范 命名规范 1、包名:使用小写字母,多个单词之间用"."分隔,例如ÿ…...

【Java集合框架】篇五:Map接口
1. Map及实现类特点 Map:存储key-value HashMap:线程不安全,效率高,key和value都可以为null,底层使用 数组单向链表红黑树 结构(jdk8)。 LinkedHashMap:是HashMap的子类࿰…...

Typroa安装教程
Markdown 是一种轻量级标记语言,创始人为约翰格鲁伯(John Gruber)。 它允许人们使用易读易写的纯文本格式编写文档,然后转换成有效的 XHTML(或者HTML)文档。这种语言吸收了很多在电子邮件中已有的纯文本标记…...
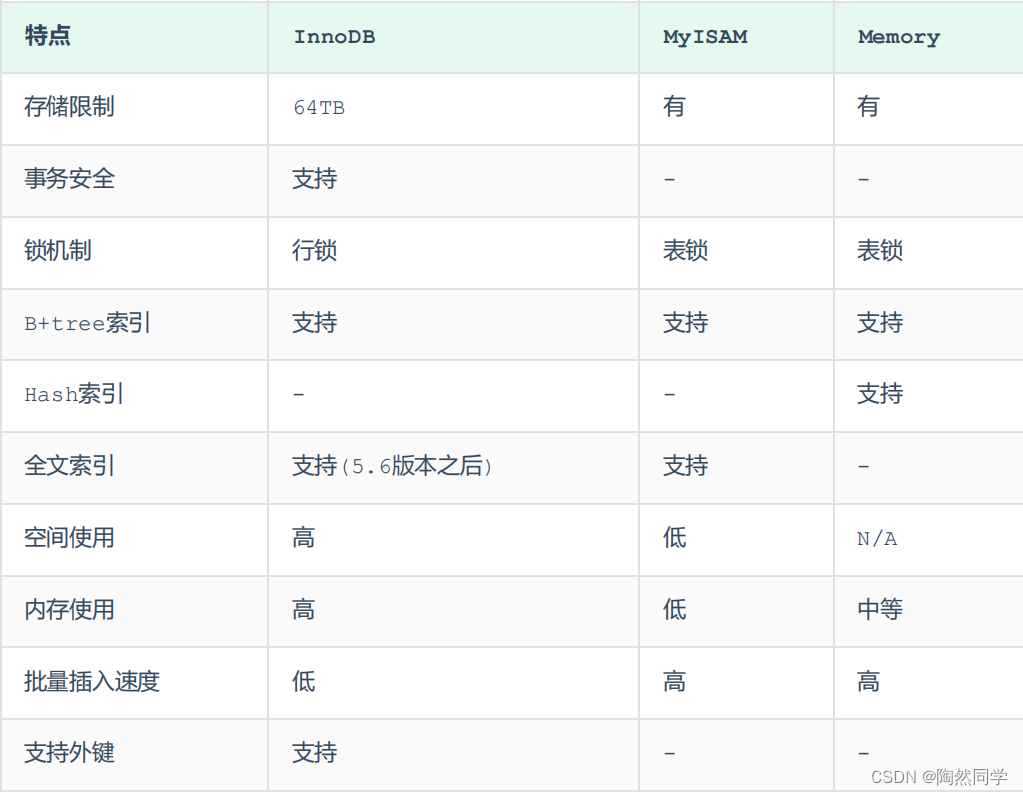
【MySQL】存储引擎
目录 1.MySQL体系结构 2.存储引擎介绍 3.存储引擎特点 4.存储引擎选择 1.MySQL体系结构 MySQL整体的逻辑结构可以分为4层,客户层、服务层、存储引擎层、数据层 客户层 客户层:进行相关的连接处理、权限控制、安全处理等操作 服务层 服务层负责与客户层进行连接处理、处…...
芯驰(E3-gateway)开发板环境搭建以及调试遇到问题的解决
1-Windows下环境配置 可以在Windows上使用命令行或者IAR IDE编译SSDK项目。Windows编译依赖的工具已经包含在 prebuilts/windows 目录中,包括编译器、Python和命令行工具。 1.1.1 CMD SSDK集成 msys 工具,可以在Windows命令行中完成SDK的配置、编译和…...
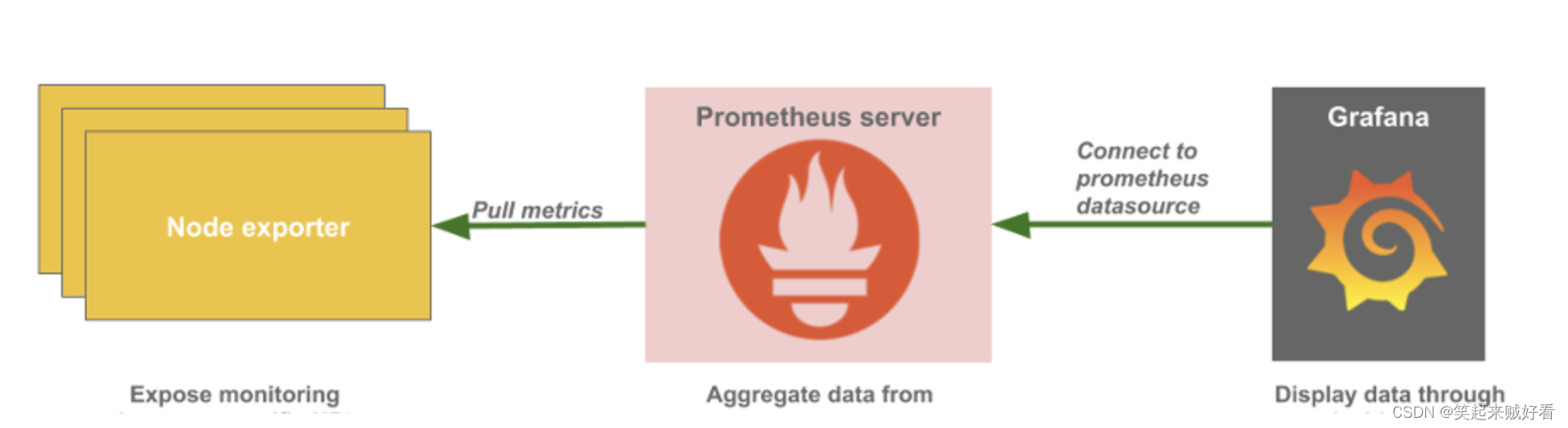
【大数据监控】Prometheus、Node_exporter、Graphite_exporter安装部署详细文档
目录Prometheus简介下载软件包安装部署创建用户创建Systemd服务修改配置文件prometheus.yml启动Prometheusnode exporter下载软件包安装部署添加用户创建systemd服务启动node_exportergraphite_exporter下载软件包安装部署创建systemd服务启动 graphite_exporterPrometheus 简介…...

《C++ Primer》 第十一章 关联容器
《C Primer》 第十一章 关联容器 11.1 使用关联容器 使用map: //统计每个单词在输入中出现的次数 map<string, size_t> word_count;//string到size_t的空map string word; while(cin>>word)word_count[word];//提取word的计数器并将其加1 for(const auto &w:…...

WebRTC标准与框架解读(1)
1、如果让我来设计webrtc框架我在分析源码的时候,都喜欢做这样一件事情:如果让我来设计它,我会怎么做?大家可以紧跟我的思路,分析一下WebRTC为什么如此设计。为了对整个框架有有一个全面的了解,我们首先要做…...
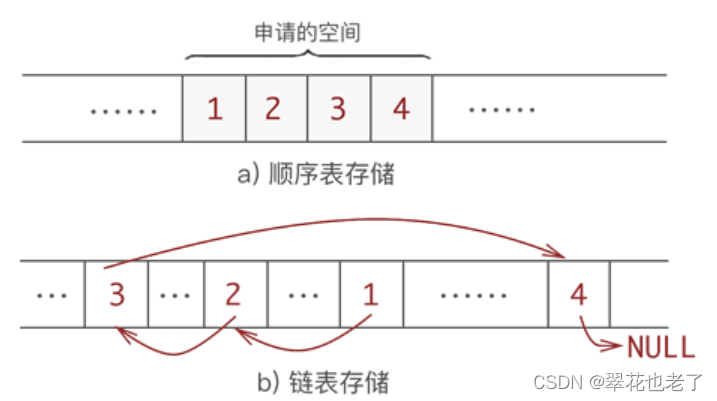
数据结构的一些基础概念
一 基本术语 数据:是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的符号集合。 数据元素:是组成数据的,有一定意义的基本单位,在计算机中通常作为整体处…...

【Python每日一练】总目录(不断更新中...)
Python 2023.03 20230303 1. 两数之和 ★ 2. 组合总和 ★★ 3. 相同的树 ★★ 20230302 1. 字符串统计 2. 合并两个有序链表 3. 下一个排列 20230301 1. 只出现一次的数字 2. 以特殊格式处理连续增加的数字 3. 最短回文串 Python 2023.02 20230228 1. 螺旋矩阵 …...
)
latex插入图片(自用)
加入宏包:\usepackage{graphicx} 使用 \includegraphics 命令进行插图。 \includegraphics[]{}: 第一参数[]:对图片做一些适当的调整(设定图片的高度和宽度或者按比例缩放) 第二参数{}:图片的名字…...

【微信小程序】-- 网络数据请求(十九)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

K8S 实用工具之一 - 如何合并多个 kubeconfig?
开篇 📜 引言: 磨刀不误砍柴工工欲善其事必先利其器 K8S 集群规模,有的公司倾向于少量大规模 K8S 集群,也有的公司会倾向于大量小规模的 K8S 集群。 如果是第二种情况,是否有一个简单的 kubectl 命令来获取一个 kubec…...
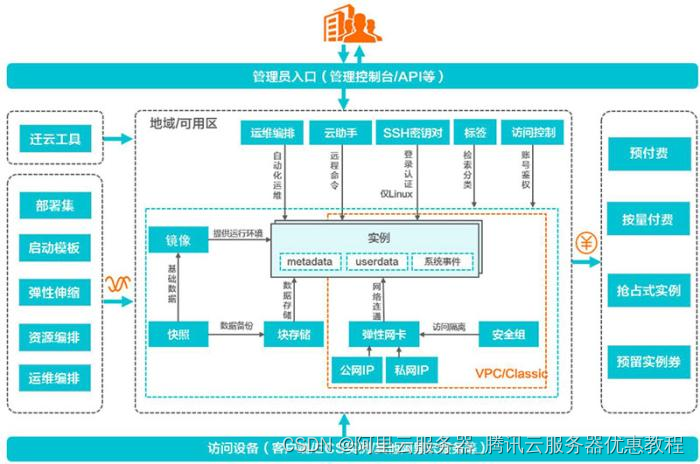
阿里云ECS服务器的6大功能组件
阿里的云服务在国内可以说是首屈一指的了,因此他们家的云服务器也是最受欢迎的。那么,你知道阿里云服务器ECS有哪些功能组件吗?不清楚不要紧,下面服务器吧小编带大家来看看。 在了解之前我们来看一张阿里云服务器ECS的产品组件架…...

外贸建站多少钱?不同预算对应的建站方案!
外贸建站多少钱? 答案是:3000左右。 作为一个外贸企业的经营者,我们深知一个优质的外贸网站对于企业的重要性。 然而,建立一个优质的外贸网站需要耗费大量的时间和资金,因此我们需要在预算有限的情况下,…...
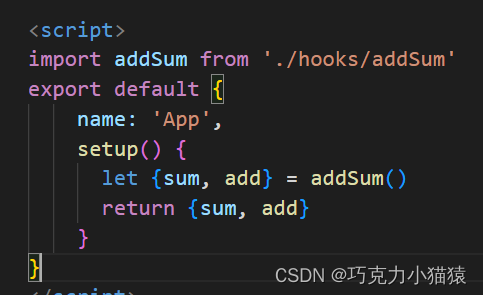
Vue3中hook的使用及使用中遇到的坑
目录前言一,什么是hook二, hook函数的使用2.1 铺垫2.2 hook函数的写法2.3 使用写好的hook函数后记前言 在学习Es6的时候,我们开始使用类与对象,开始模块化管理;在Vue中我们可以使用mixin进行模块化管理;Vu…...

数据库-差集交集并集
数据库-差集交集并集[toc]图示一、并集运算(UNION)并集:两个集合的并集是一个包含集合A和B中所有元素的集合。在T-SQL中,UNION集合运算可以将两个输入查询的结果组合成一个结果集。需要注意的是:如果一个行在任何一个输…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...
