模拟算法(模拟算法 == 依葫芦画瓢)万字
模拟算法
- 基本思想
- 引入算法题
- 替换所有的问号
- 提莫攻击
- Z字形变换
- 外观数列
- 数青蛙
基本思想
模拟算法 == 依葫芦画瓢解题思维要么通俗易懂,要么就是找规律,主要难度在于将思路转换为代码。
- 特点:相对于其他算法思维,思路比较简单(没有很多的弯弯绕绕,考察的是代码能力)。
- 大致做题流程
- 模拟算法流程
(一定要在演草纸上过一遍 - 容易忽略细节) - 把流程转换为代码
- 模拟算法流程
引入算法题
替换所有的问号
链接:https://leetcode.cn/problems/replace-all-s-to-avoid-consecutive-repeating-characters/description/
给你一个仅包含小写英文字母和 ‘?’ 字符的字符串 s,请你将所有的 ‘?’ 转换为若干小写字母,使最终的字符串不包含任何 连续重复 的字符。
注意: 你不能修改非 ‘?’ 字符。
题目测试用例保证除 ‘?’ 字符之外,不存在连续重复的字符。
在完成所有转换(可能无需转换)后返回最终的字符串。如果有多个解决方案,请返回其中任何一个。可以证明,在给定的约束条件下,答案总是存在的。
示例 1:
输入:s = “?zs”
输出:"azs"
解释:该示例共有 25 种解决方案,从 "azs" 到 "yzs" 都是符合题目要求的。只有 "z" 是无效的修改,因为字符串 "zzs" 中有连续重复的两个 'z'。
题目分析:
题目讲的很清楚,就是替换 '?' ,使其变为小写字母,并需保证无连续重复字符。
解题:
- 1、模拟算法流程
容易忽略细节:最左端与最右端两种情况。

- 2、把流程转换为代码
class Solution {
public:string modifyString(string s) {int size = s.size();for(int i = 0; i < size; i++){if(s[i] == '?'){for(char ch = 'a'; ch <= 'z'; ch++){if((i == 0 || s[i - 1] != ch) && (i == size - 1 || s[i + 1] != ch))s[i] = ch;}}}return s;}
};
提莫攻击
链接:https://leetcode.cn/problems/teemo-attacking/description/
在《英雄联盟》的世界中,有一个叫 “提莫” 的英雄。他的攻击可以让敌方英雄艾希(编者注:寒冰射手)进入中毒状态。
当提莫攻击艾希,艾希的中毒状态正好持续 duration 秒。
正式地讲,提莫在 t 发起攻击意味着艾希在时间区间 [t, t + duration - 1](含 t 和 t + duration - 1)处于中毒状态。如果提莫在中毒影响结束 前 再次攻击,中毒状态计时器将会 重置 ,在新的攻击之后,中毒影响将会在 duration 秒后结束。
给你一个 非递减 的整数数组 timeSeries ,其中 timeSeries[i] 表示提莫在 timeSeries[i] 秒时对艾希发起攻击,以及一个表示中毒持续时间的整数 duration 。
返回艾希处于中毒状态的 总 秒数。
示例 2:
输入:timeSeries = [1,2], duration = 2
输出:3
解释:提莫攻击对艾希的影响如下:
第 1 秒:提莫攻击艾希并使其立即中毒。中毒状态会维持 2 秒,即第 1 秒和第 2 秒。
第 2 秒:提莫再次攻击艾希,并重置中毒计时器,艾希中毒状态需要持续 2 秒,即第 2 秒和第 3 秒。
艾希在第 1、2、3 秒处于中毒状态,所以总中毒秒数是 3 。
题目分析:
题目讲的很清楚,就是计算中毒的有效时间,但是中毒是有时效的,并且时间可能重叠。
解题:
- 1、模拟算法流程
容易忽略细节:两次投毒时间之间的时间与,中毒有效时间duration的关系。
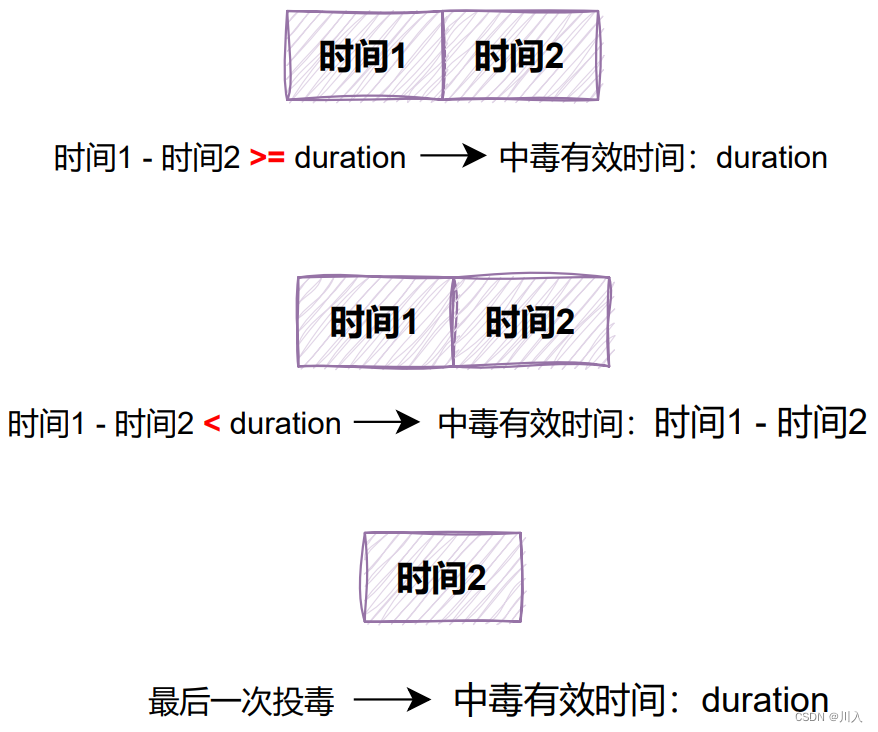
- 2、把流程转换为代码
class Solution {
public:int findPoisonedDuration(vector<int>& timeSeries, int duration) {int ret = 0;for(int i = 0; i < timeSeries.size() - 1; i++){int tmp = timeSeries[i + 1] - timeSeries[i];if(tmp >= duration)ret += duration;elseret += tmp;}ret += duration;return ret;}
};
Z字形变换
链接:https://leetcode.cn/problems/zigzag-conversion/
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 “PAYPALISHIRING” 行数为 3 时,排列如下:
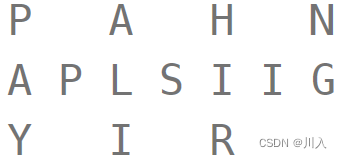
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:“PAHNAPLSIIGYIR”。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = “PAYPALISHIRING”, numRows = 3
输出:“PAHNAPLSIIGYIR”
题目分析:
题目讲的很清楚,从上往下、从左到右进行Z 字形排列。之后,从左往右逐行读取。
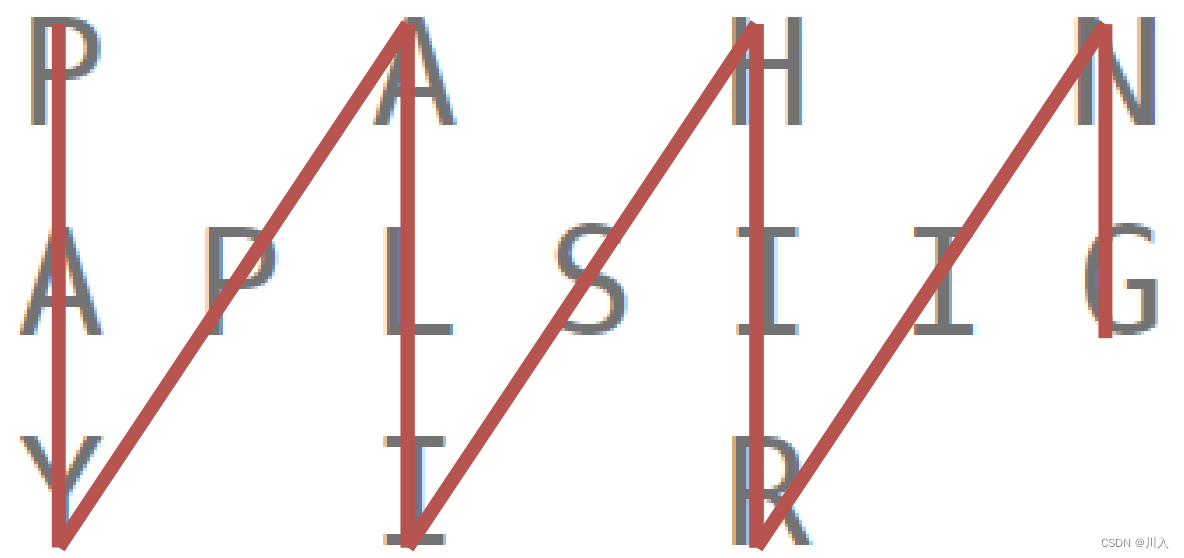
解题:
- 1、模拟算法流程
最直接暴力的方式就是:利用二维数组进行解题 - 可想而知空间复杂度与时间复杂度都是极高的!
99.99%的模拟题的优化方式都是找规律。
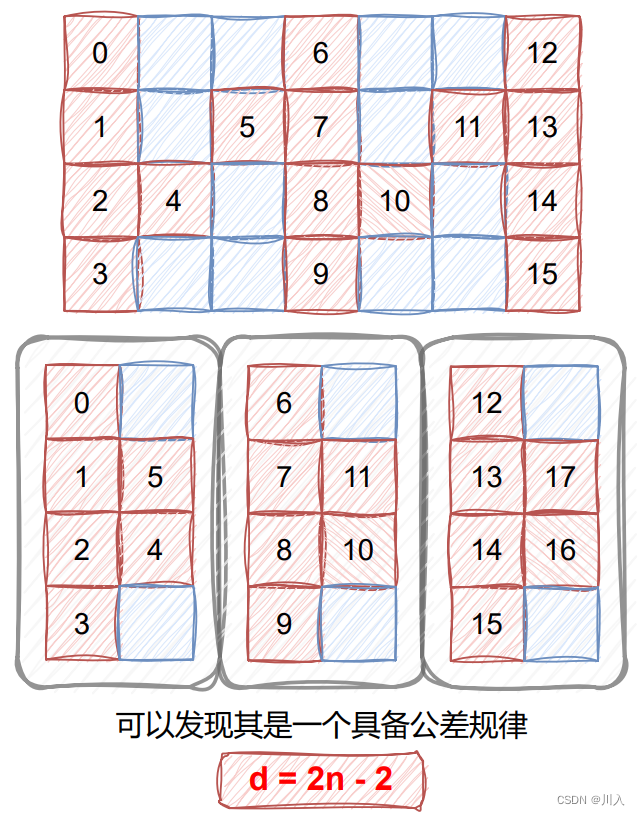
以此可以发现一个规律。
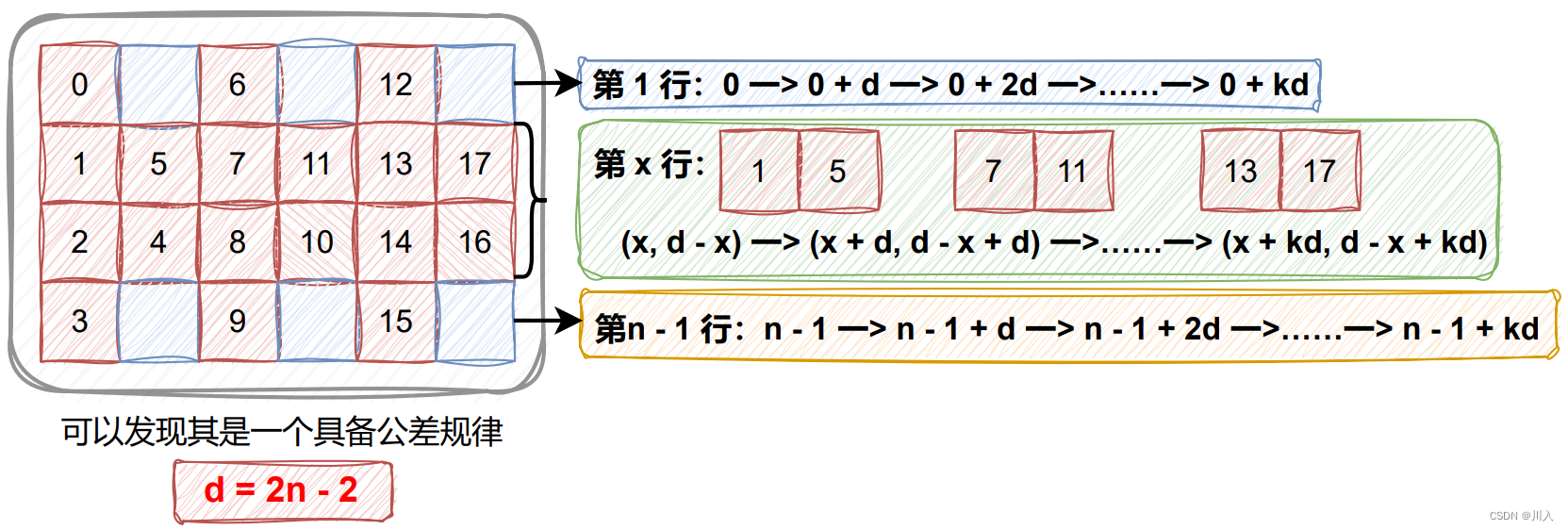
- 2、把流程转换为代码
class Solution {
public:string convert(string s, int numRows) {if(numRows == 1)return s;int size = s.size();int d = 2 * numRows - 2;string ret;// 第一行for(int i = 0; i < size; i += d){ret += s[i];}// (1, numRows - 1)行for(int k = 1; k < numRows - 1; k++){for(int i = k, j = d - k; i < size; i += d, j += d){if(i < size)ret += s[i];if(j < size)ret += s[j];}}// 第numRows - 1行for(int i = numRows - 1; i < size; i += d){ret += s[i];}return ret;}
};
外观数列
链接:https://leetcode.cn/problems/count-and-say/description/
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
- countAndSay(1) = “1”
- countAndSay(n) 是对 countAndSay(n-1) 的描述,然后转换成另一个数字字符串。
前五项如下:
1、 1
2、 11
3、 21
4、 1211
5、 111221
第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 “11”
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 “21”
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 “1211”
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 “111221”
要描述一个数字字符串,首先要将字符串分割为最小数量的组,每个组都由连续的最多相同字符组成。然后对于每个组,先描述字符的数量,然后描述字符,形成一个描述组。要将描述转换为数字字符串,先将每组中的字符数量用数字替换,再将所有描述组连接起来。
例如,数字字符串 “3322251” 的描述如下图:

示例 1:
输入:n = 1
输出:"1"
解释:这是一个基本样例。
题目分析:
题目讲的很清楚,从上往下、从左到右下一行是上一行的元素描述。
解题:
- 1、模拟算法流程
该题通过寻找发现并无任何规律,是模拟 + 双指针的方法。
- 模拟: 依葫芦画瓢,对上一行数据进行描述。
- 双指针: 通过
分三块,分为[已被记录区域],[等待记录区域],[等得被记录区域]。 - 2、把流程转换为代码
class Solution {
public:string countAndSay(int n) {string ret = "1";for(int i = 1; i < n; i++){string tmp;int left = 0, right = 0;while(right < ret.size()){while(right < ret.size() && ret[left] == ret[right]) right++;tmp += to_string(right - left);tmp += ret[left];left = right;}ret = tmp;}return ret;}
};
数青蛙
链接:https://leetcode.cn/problems/minimum-number-of-frogs-croaking/description/
给你一个字符串 croakOfFrogs,它表示不同青蛙发出的蛙鸣声(字符串 “croak” )的组合。由于同一时间可以有多只青蛙呱呱作响,所以 croakOfFrogs 中会混合多个 “croak” 。
请你返回模拟字符串中所有蛙鸣所需不同青蛙的最少数目。
要想发出蛙鸣 “croak”,青蛙必须 依序 输出 ‘c’, ’r’, ’o’, ’a’, ’k’ 这 5 个字母。如果没有输出全部五个字母,那么它就不会发出声音。如果字符串 croakOfFrogs 不是由若干有效的 “croak” 字符混合而成,请返回 -1 。
示例 1:
输入:croakOfFrogs = “croakcroak”
输出:1
解释:一只青蛙 “呱呱” 两次
题目分析:
需要按序组成以此青蛙叫"croak",才算一只青蛙,但是一只叫完的青蛙可以再接着再"croak"一次,所以青蛙的数量不算增加!
解题:
- 1、模拟算法流程
需要使用到
哈希
当遇到 ‘r’ ‘o’ ‘a’ ‘k’ 这四个字符的时候,我们要去看看每⼀个字符对应的前驱字符,有没有青蛙叫出来。如果有青蛙叫出来,那就让这个青蛙接下来喊出来这个字符;如果没有,直接返回 -1 ;
当遇到 ‘c’ 这个字符的时候,我们去看看 ‘k’ 这个字符有没有青蛙叫出来。如果有,就让这个青蛙继续去喊 ‘c’ 这个字符;如果没有的话,就重新搞⼀个青蛙。
总结:
r, o, a, k:找一下前驱字符,是否在哈希表中存在?存在:前驱--,当前++。不存在:返回-1。
c:找最后一个字符,是否在哈希表中存在?存在:最后一个--,当前++。不存在:当前++。
- 2、把流程转换为代码
class Solution {
public:int minNumberOfFrogs(string croakOfFrogs) {vector<int> hash(5, 0);string tmp = "croak";int n = tmp.size();unordered_map<char, int> index; //[x, x这个字符对应的下标]for(int i = 0; i < n; i++)index[tmp[i]] = i;for(auto ch : croakOfFrogs){if(ch == 'c'){if(hash[n - 1] != 0) hash[n - 1]--;hash[0]++;}else{int i = index[ch];if(hash[i - 1] == 0)return -1;hash[i - 1]--;hash[i]++;}}for(int i = 0; i < n - 1; i++){if(hash[i] != 0)return -1;}return hash[4];}
};
相关文章:

模拟算法(模拟算法 == 依葫芦画瓢)万字
模拟算法 基本思想引入算法题替换所有的问号提莫攻击Z字形变换外观数列数青蛙 基本思想 模拟算法 依葫芦画瓢解题思维要么通俗易懂,要么就是找规律,主要难度在于将思路转换为代码。 特点:相对于其他算法思维,思路比较简单&#x…...

QtApplets-SystemInfo
QtApplets-SystemInfo 今天是2024年1月3日09:18:44,这也是2024年的第一篇博客,今天我们主要两件事,第一件,获取系统CPU使用率,第二件,获取系统内存使用情况。 这里因为写博客的这个本本的环境配置不…...

vue3防抖函数封装与使用,以指令的形式使用
utils/debounce.js /*** 防抖函数* param {*} fn 函数* param {*} delay 暂停时间* returns */ export function debounce(fn, delay 500) {let timer nullreturn function (...args) {// console.log(arguments);// const args Array.from(arguments)if (timer) {clearTim…...
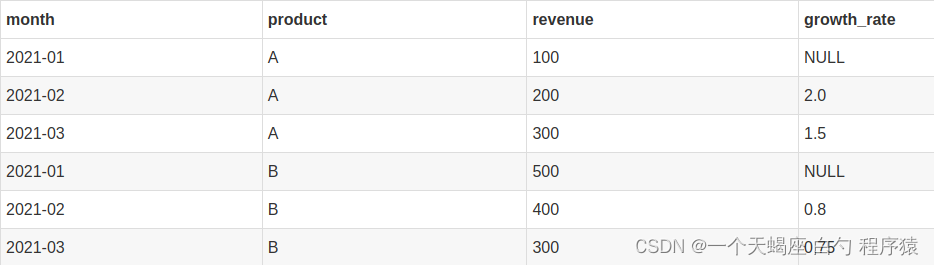
Hive学习(13)lag和lead函数取偏移量
hive里面lag函数 在数据处理和分析中,窗口函数是一种重要的技术,用于在数据集中执行聚合和分析操作。Hive作为一种大数据处理框架,也提供了窗口函数的支持。在Hive中,Lag函数是一种常用的窗口函数,可以用于计算前一行…...

Centos Unable to verify the graphical display setup
ERROR: Unable to verify the graphical display setup. 在Linux下安装Oracle时 运行 ./runInstaller 报错 ERROR: Unable to verify the graphical display setup. This application requires X display. Make sure that xdpyinfo exist under PATH variable. No X11 DISPL…...

Java 说一下 synchronized 底层实现原理?
Java 说一下 synchronized 底层实现原理? synchronized 是 Java 中用于实现同步的关键字,它保证了多个线程对共享资源的互斥访问。底层实现涉及到对象头的 Mark Word 和锁升级过程。 synchronized 可以用于方法上或代码块上,分别对应于方法…...

nginx访问路径匹配方法
目录 一:匹配方法 二:location使用: 三:rewrite使用 一:匹配方法 location和rewrite是两个用于处理请求的重要模块,它们都可以根据请求的路径进行匹配和处理。 二:location使用: 1:简单匹配…...

偌依 项目部署及上线步骤
准备实验环境,准备3台机器 1.作为前端服务器,mysql,redis服务器--同时临时作为代码打包服务器 192.168.2.65 nginx-server 2.作为后端服务器 192.168.2.66 java-server-1 192.168.2.67 java-server-2 安装nginx/mysql #安装nginx [rootweb-nginx ~]…...

PHP特性知识点扫盲 - 上篇
概述 之前在分析thinkphp源码的时候,对依赖注入等等php高级的特性一直想做一个梳理和总结,一直没有时间,好不容易抽一点时间对技术的盲点做一个扫盲和总结。 特性 1.命名空间 命名空间是在PHP5.3中引入,是一个很重要的工具&am…...
Docker一键极速安装Nacos,并配置数据库!
1 部署方式 1.1 DockerHub javaedgeJavaEdgedeMac-mini ~ % docker run --name nacos \ -e MODEstandalone \ -e JVM_XMS128m \ -e JVM_XMX128m \ -e JVM_XMN64m \ -e JVM_MS64m \ -e JVM_MMS64m \ -p 8848:8848 \ -d nacos/nacos-server:v2.2.3 a624c64a1a25ad2d15908a67316d…...
交换机04_远程连接
通过远程管理方式连接交换机 1、telnet简介 telnet 是应用层协议 基于传输层TCP协议的,默认端口:23 采用的是明文密码方式 不是很安全,一般用于内网管理。 2、ssh协议简介 ssh 是应用层的协议,基于传输层的TCP协议&#x…...
, 实现继承?)
ES6定义一个类(函数内部定义属性,,原型定义方法 ), 实现继承?
ES6中使用class关键字定义一个类,使用extends关键字实现继承。下面是一个示例: class Animal {constructor(name) {this.name name;}sayHello() {console.log(Hello, my name is ${this.name});} }class Dog extends Animal {constructor(name, breed)…...
使用 Process Explorer 和 Windbg 排查软件线程堵塞案例分享
目录 1、问题说明 2、线程堵塞的可能原因分析 3、使用Windbg和Process Explorer确定线程中发生了死循环 4、根据Windbg中显示的函数调用堆栈去查看源码,找到问题 4.1、在Windbg定位发生死循环的函数的方法 4.2、在Windbg中查看变量的值去辅助分析 4.3、是循环…...

“智慧”千里眼助力水泵站
泵站是为水提供势能和压能,解决无自流条件下的排灌、供水和水资源调配问题的唯一动力来源,在工农业用水、防洪、排涝和抗旱减灾等方面发挥着重要作用。一旦出现异常,对经济生产将造成难以估量的损失,给水利安全管理造成负担。因此…...

C++多态性——(5)运算符重载(第二节)
归纳编程学习的感悟, 记录奋斗路上的点滴, 希望能帮到一样刻苦的你! 如有不足欢迎指正! 共同学习交流! 🌎欢迎各位→点赞 👍 收藏⭐ 留言📝 身先才能率人,律己才能服人…...
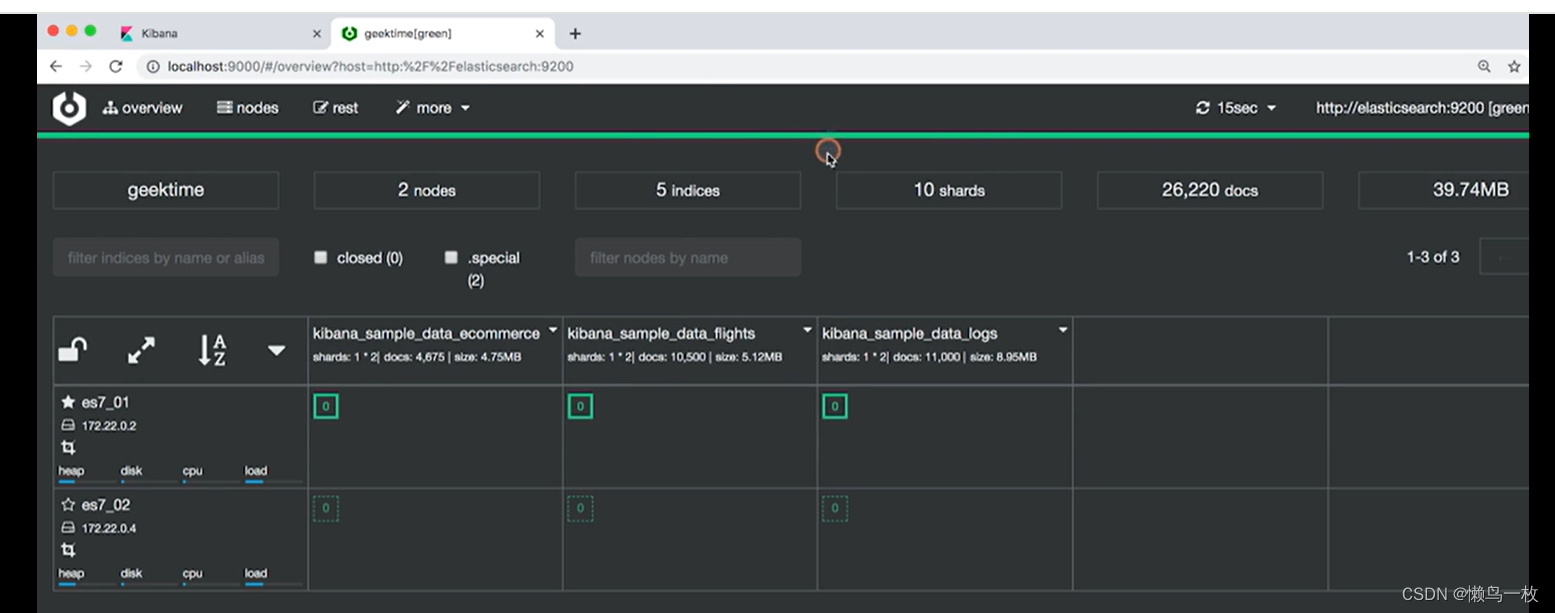
ES -极客学习
Elasticsearch 简介及其发展历史 起源 Lucene 于 Java 语言开发的搜索引擎库类创建于 1999 年,2005 年成为 Apache 顶级开源项目Lucene 具有高性能、易扩展的优点Lucene 的局限性 只能基于 Java 语言开发类库的接口学习曲线陡峭原生并不支持水平扩展原生并不支持水…...

【大厂秘籍】系列 - Java多线程面试题
Java多线程面试题 友情提示,看完此文,在Java多线程这块,基本上可以吊打面试官了 线程和进程的区别 进程是资源分配的最小单位,线程是CPU调度的最小单位 线程是进程的子集,一个进程可以有很多线程,每条线…...

vue实现画笔回放,canvas转视频播放功能
示例图: 一、vue2版本 <template><div class"canvas-video"><canvasref"myCanvasByVideo"class"myCanvas"id"myCanvasByVideo":width"width":height"height"></canvas><d…...

Docker中镜像的相关操作
1.辅助操作 docker version:用查看docker客户端引擎和server端引擎版本信息。 docker info:用来查看docker引擎的详细信息。 docker --help:用来查看帮助信息。 2.镜像Image docker images:查看当前本地仓库中存在哪些镜像。 …...
[python]python利用pyaudio录制系统声音没有立体声混音怎么录制系统音频
当电脑没有立体声混音导致Python写代码无法使用pyaudio进行录制系统声音怎么办?查阅资料和安装驱动等方法都不行,难道没办法了吗?那为什么电脑其他软件可以做到呢?因此研究了一下pyaudio在没有立体声混音情况下确实无法录制声音&a…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
