当前位置： 首页 > news >正文

概率论与数理统计 知识点+课后习题

news 2026/2/8 9:48:27

文章目录

💖 学习资源整合

📚 总复习

📙 选择题

在这里插入图片描述

在这里插入图片描述

📙 填空题

在这里插入图片描述

在这里插入图片描述

📙 大题

1. 概率

在这里插入图片描述

2. 概率

在这里插入图片描述

3. 概率

在这里插入图片描述

4. P

在这里插入图片描述

5. 概率

在这里插入图片描述

6. 概率密度函数 F ( X ) F(X) F(X)

在这里插入图片描述

7. 分布列求方差 V ( X ) V(X) V(X)

在这里插入图片描述

8. 求分布函数 F ( X ) F(X) F(X)

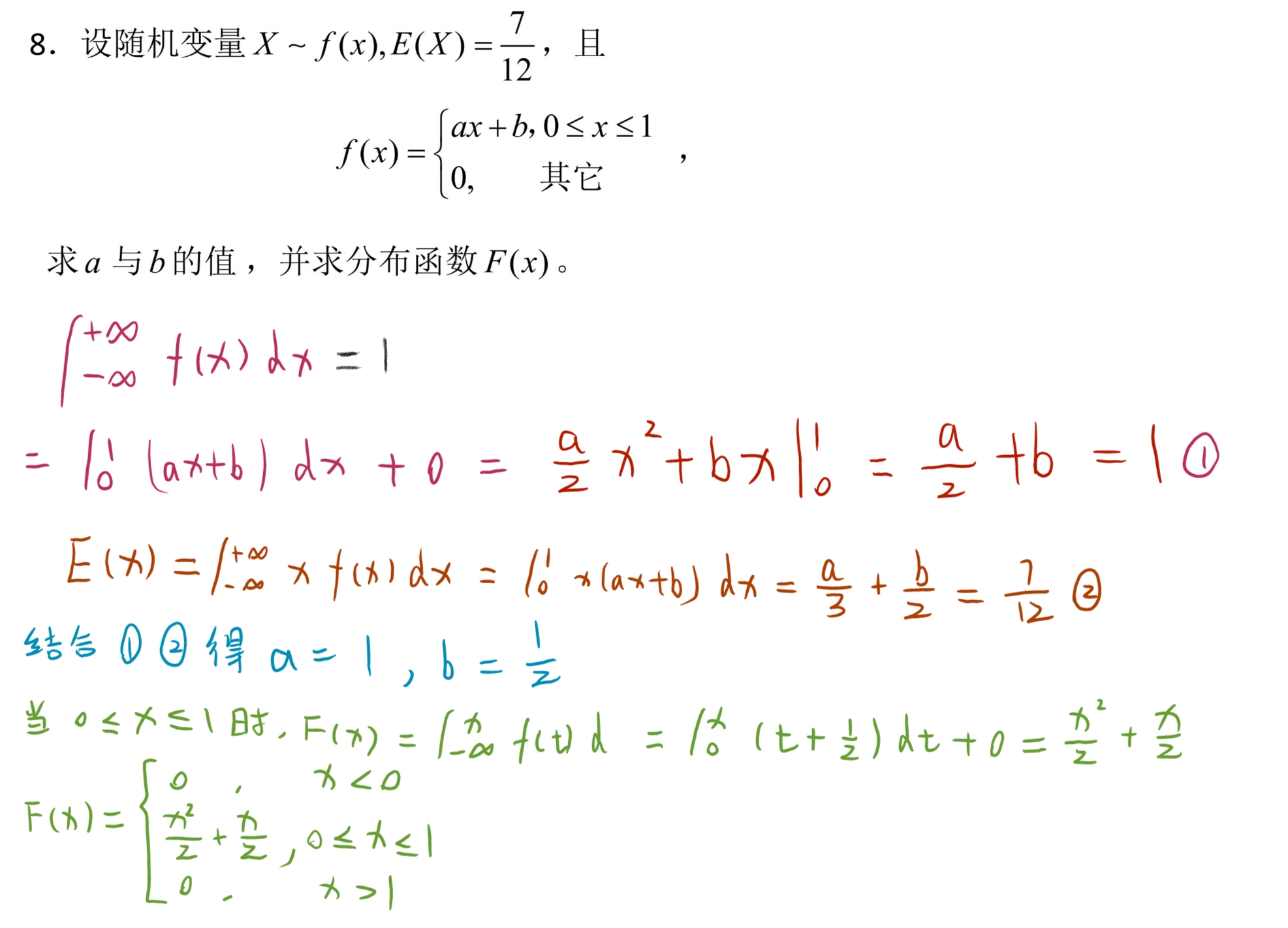
在这里插入图片描述

💖 速成课

一、事件的概率

1. 无放回类题目

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

2. 有放回类的题目

在这里插入图片描述

在这里插入图片描述

3. 需要画图的题目

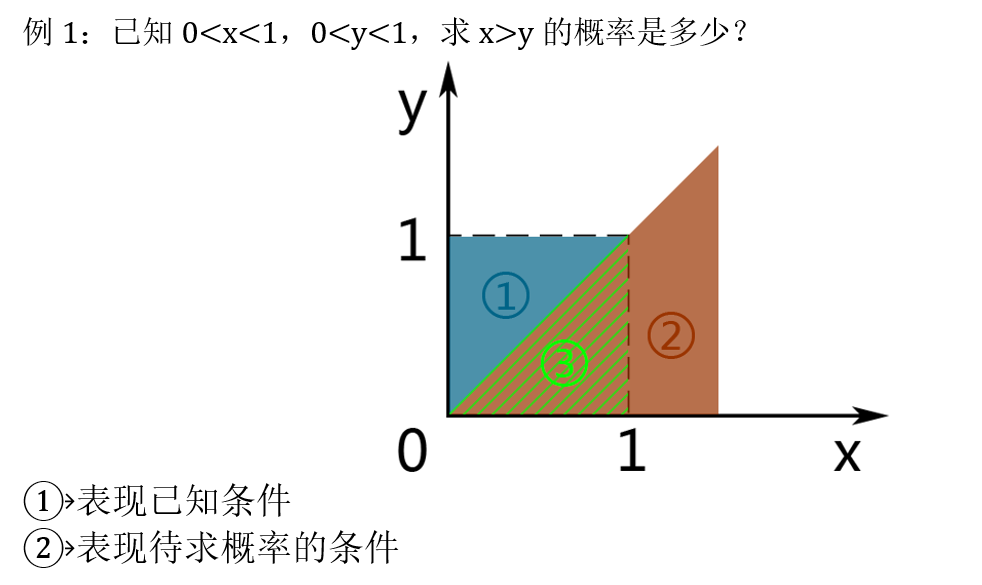
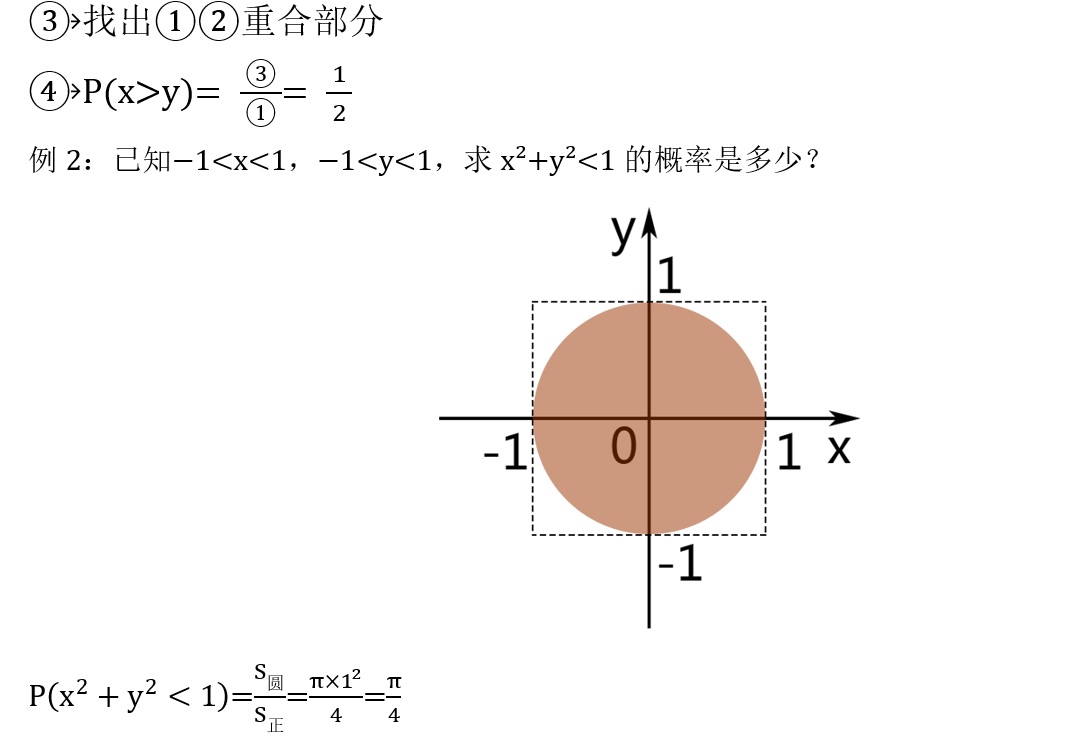
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

4. 条件概率

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

5. 全概率公式

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

6. 贝叶斯公式

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

二、一维随机变量

1. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 知一求二

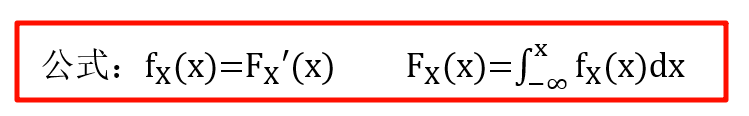
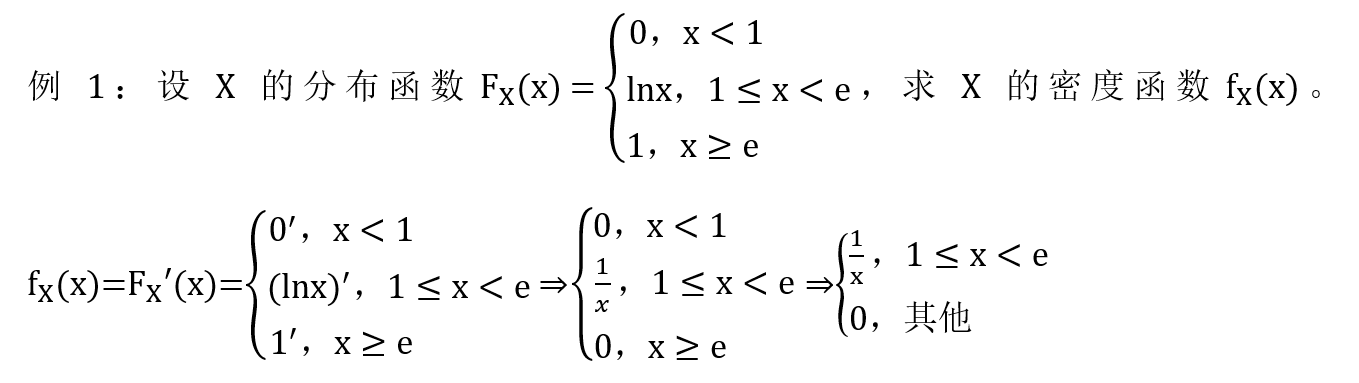
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

2. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 知一求 P P P

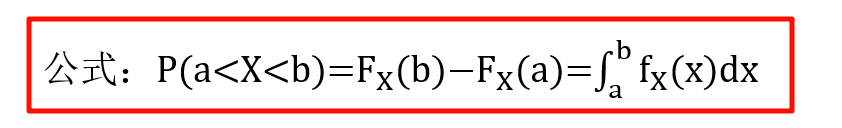
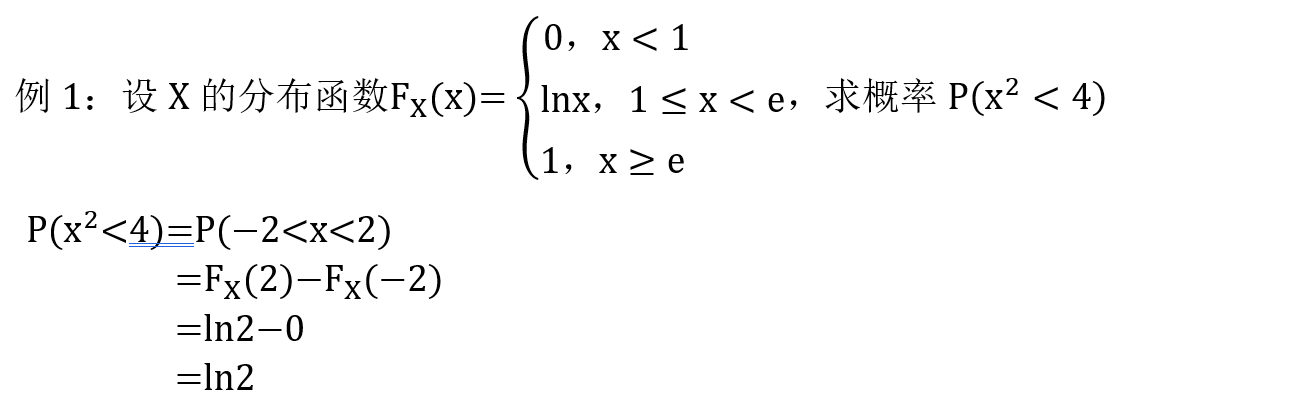
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

3. F ( x ) 和 f ( x ) F(x) 和 f(x) F(x)和f(x) 含未知数，求未知数

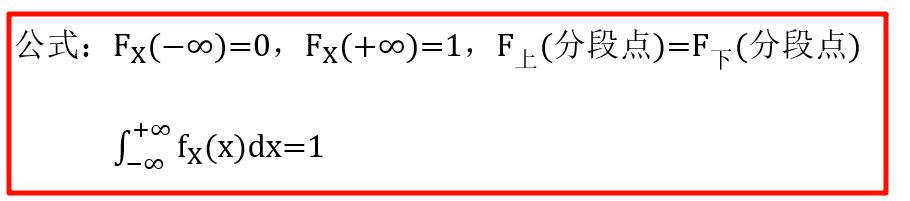
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

4. 求分布律

在这里插入图片描述

5. 已知含有未知数的分布列，求未知数

在这里插入图片描述

三、一维随机变量函数

1. 已知 X 分布列，求 Y 分布列

在这里插入图片描述

在这里插入图片描述

2. 已知 F X ( x ) F_X (x) FX​(x)，求 F Y ( y ) F_Y (y) FY​(y)

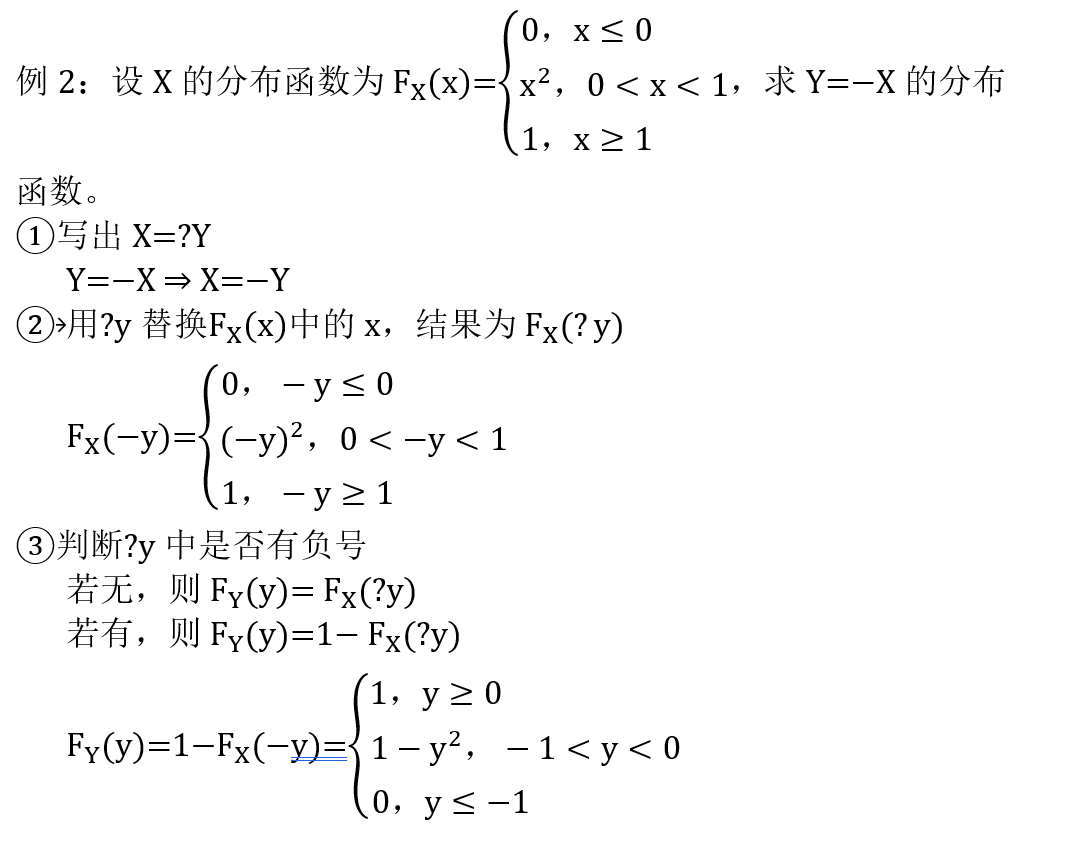
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

3. 已知 f X ( x ) f_X (x) fX​(x)，求 f Y ( y ) f_Y (y) fY​(y)

在这里插入图片描述

四、五种常见的分布

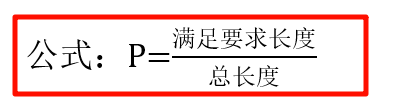
在这里插入图片描述

1. 均匀分布

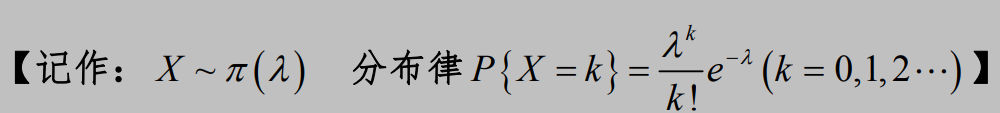
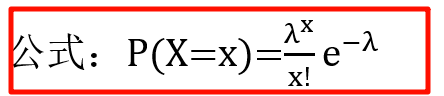
在这里插入图片描述

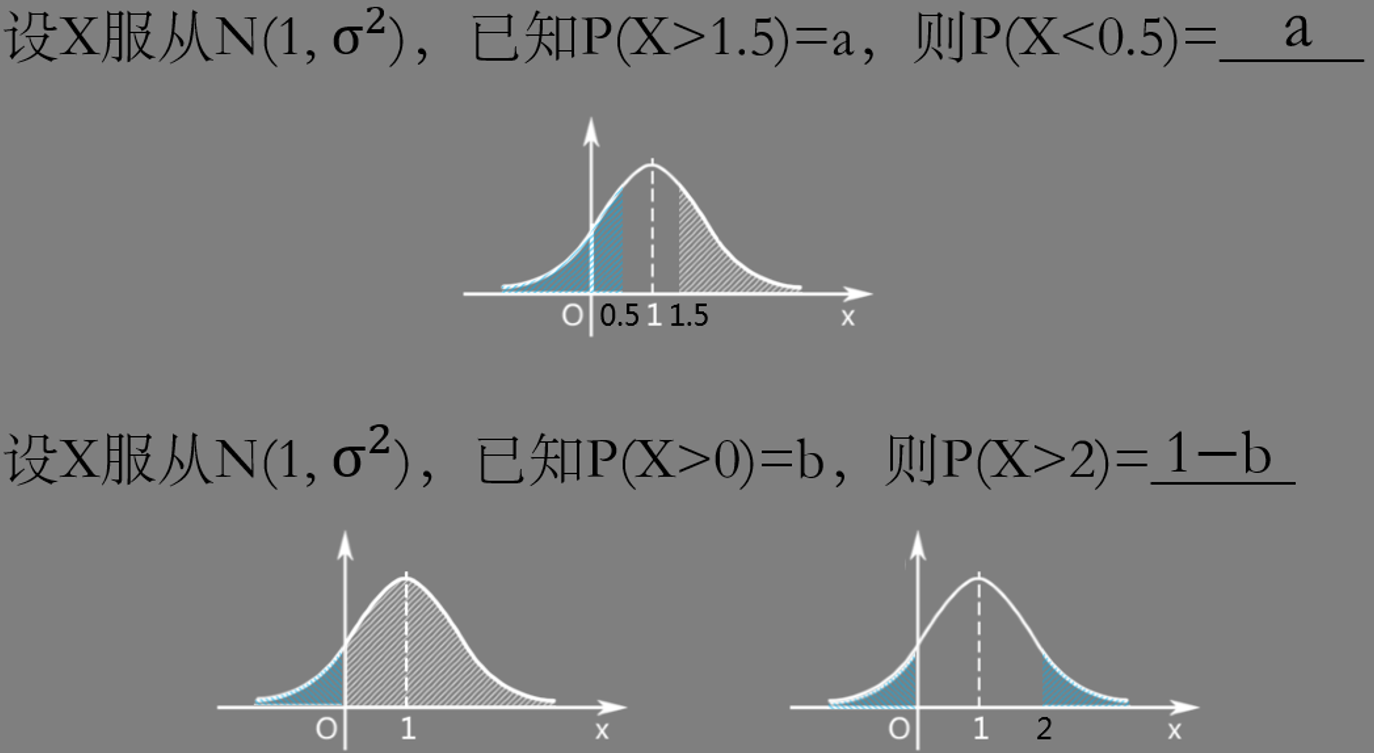
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

2. 泊松分布

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

3. 二项分布

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

4. 指数分布

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

5. 正态分布

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

6. 正态分布图像

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

五、二维随机变量

1. 二维离散型分布律求概率

在这里插入图片描述
在这里插入图片描述

2. 二维离散型分布律求独立性

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

3. 知 F ( x , y ) F(x,y) F(x,y) 求 f ( x , y ) f(x,y) f(x,y)

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4. 知 f ( x , y ) f(x,y) f(x,y) 求 F ( x , y ) F(x,y) F(x,y)

在这里插入图片描述在这里插入图片描述在这里插入图片描述

在这里插入图片描述在这里插入图片描述在这里插入图片描述

5. 已知 F ( x , y ) F(x,y) F(x,y) 求 P P P

在这里插入图片描述在这里插入图片描述

6. 已知 f ( x , y ) f(x,y) f(x,y) 求 P P P

在这里插入图片描述

在这里插入图片描述

7. 已知 F ( x , y ) F(x,y) F(x,y) 或 f ( x , y ) f(x,y) f(x,y) 含有的未知数

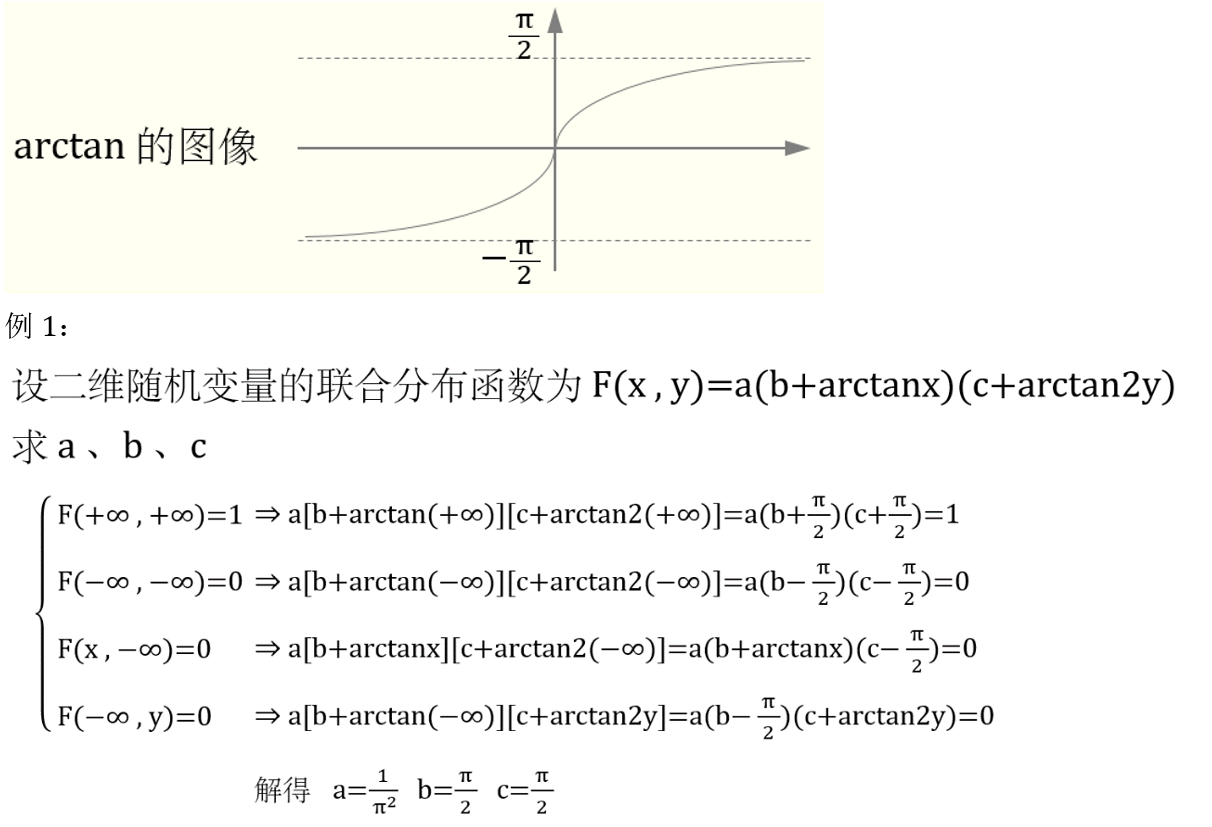
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

8. 求均匀分布的 f ( x , y ) f(x,y) f(x,y) 与 P P P

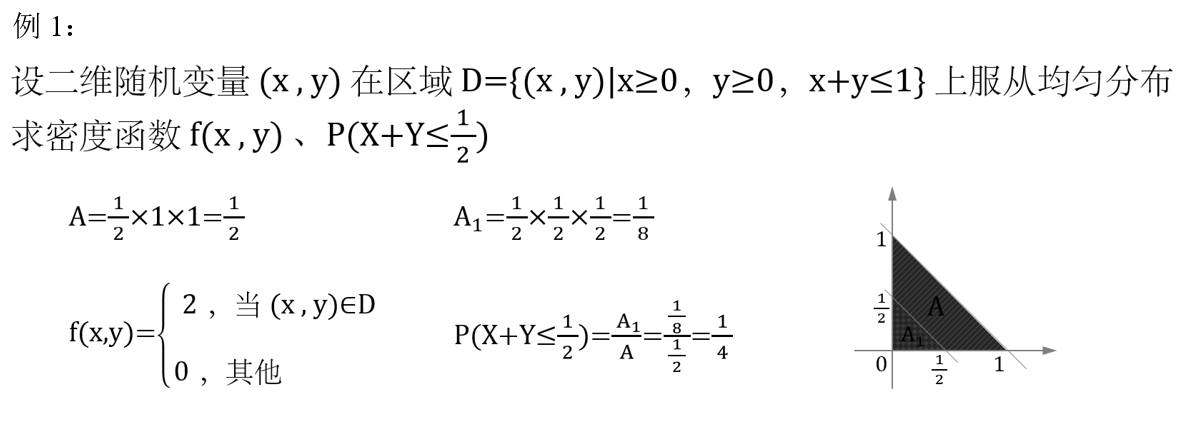
在这里插入图片描述在这里插入图片描述

六、期望与方差

1. 离散型的期望 E ( x ) E(x) E(x)

在这里插入图片描述在这里插入图片描述

2. 连续型的期望 E ( X ) E(X) E(X)

在这里插入图片描述
在这里插入图片描述

3. Y = g ( x ) Y=g(x) Y=g(x) 求 E ( Y ) E(Y) E(Y)

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

4. 方差 D ( X ) D(X) D(X)

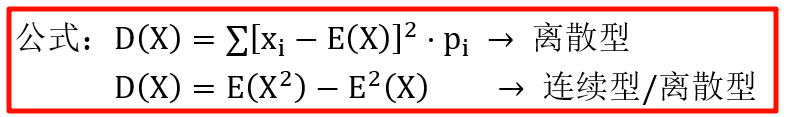
在这里插入图片描述
例1
在这里插入图片描述

在这里插入图片描述

5. 根据 E ( X ) 、 D ( X ) E(X)、D(X) E(X)、D(X) 的性质进行复杂运算 ⭐

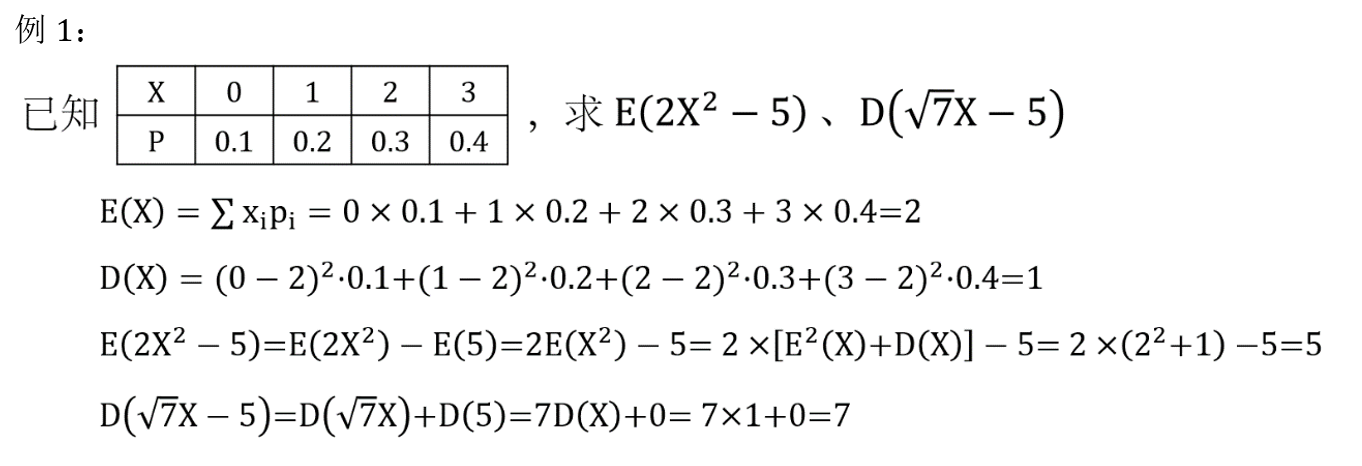
在这里插入图片描述
在这里插入图片描述

6. E ( X ) 、 D ( X ) E(X)、D(X) E(X)、D(X) 与各种分布的综合题 ⭐

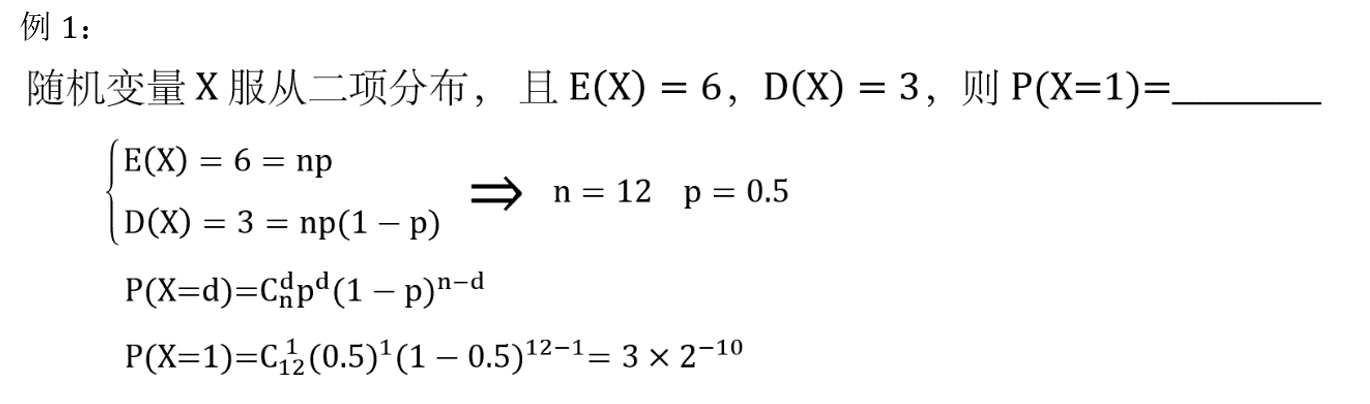
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

七、中心极限定理

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

八、抽样分布

相关文章：

概率论与数理统计 知识点+课后习题

文章目录 💖 [学习资源整合](https://www.cnblogs.com/duisheng/p/17872980.html)📚 总复习📙 选择题📙 填空题📙 大题1. 概率2. 概率3. 概率4. P5. 概率6. 概率密度函数 F ( X ) F(X) F(X)7. 分布列求方差 V ( X ) …...

编程日记 2024/1/7 14:25:04

Spring Boot实战：深入理解@Service与@Mapper注解

1. Service 注解 Service 是Spring框架提供的一个注解，用于标记类为业务逻辑层的组件。当类上标注了Service注解后，Spring容器会自动扫描并创建该类的一个实例（即Bean），这样我们就可以在其他地方通过自动装配&#xf…...

编程日记 2024/1/7 14:23:03

【DevOps-06】Jenkins实现CI/CD操作

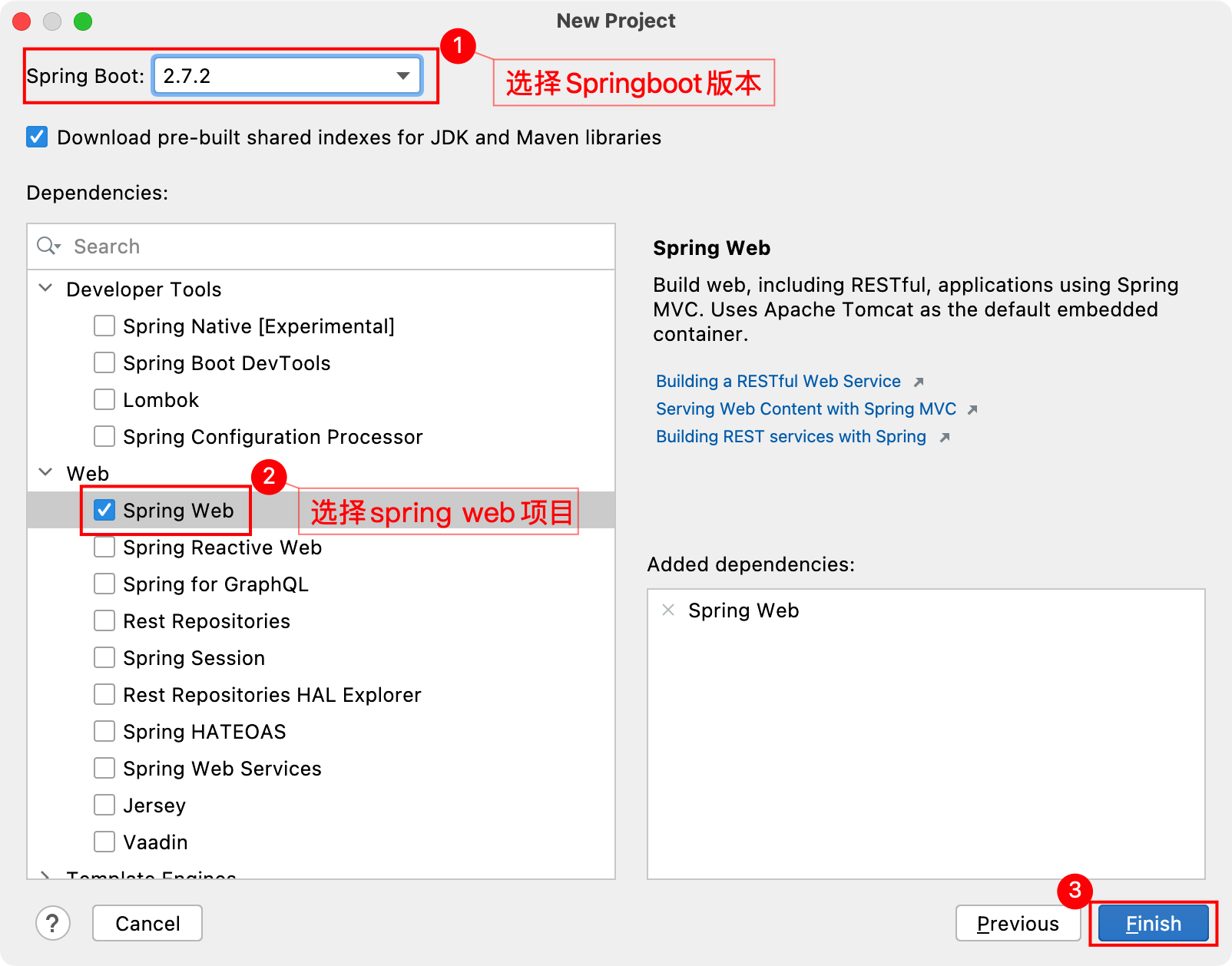
一、简要说明 基于Jenkins拉取GitLab的SpringBoot代码进行构建发布到测试环境实现持续集成 基于Jenkins拉取GitLab指定发行版本的SpringBoot代码进行构建发布到生产环境实现CD实现持续部署 二、准备Springboot工程 1、IDEA新建工程 2、填写项目工程信息 3、选择Springboot版本…...

编程日记 2024/1/7 14:22:02

华为面经总结

为了帮助大家更好的应对面试，我整理了往年华为校招面试的题目，供大家参考~ 面经1 技术一面 自我介绍说下项目中的难点volatile和synchronized的区别， 问的比较细大顶堆小顶堆怎么删除根节点CSRF攻击是什么，怎么预防线程通信方式…...

编程日记 2024/1/7 14:17:58

大模型实战营Day1 书生·浦语大模型全链路开源体系

1.大模型为发展通用人工智能的重要途经 专用模型：针对特定任务解决特定问题 通用大模型：一个模型对应多模态多任务 2.InternLM大模型开源历程 3.InternLM-20B大模型性能 4.从模型到应用：智能客服、个人助手、行业应用 5.书生浦语全链条开源…...

编程日记 2024/1/7 14:15:56

Java 集合面试题真实场景还原

Java 集合面试题真实场景还原 文章目录 Java 集合面试题真实场景还原Java常见的集合类ListHashMap Java常见的集合类 面试官：说一说Java提供的常见集合？（画一下集合结构图） 候选人： 嗯~~，好的。 在java中提…...

编程日记 2024/1/7 14:13:54

AutoSAR（基础入门篇）4.9-Autoar_BSW小结

Autoar_BSW小结 Autoar_BSW小结 一、Autoar_BSW小结 1、BSW组件图 2、BSW的功能概述 3、BSW在工程里的应用实际工程...

编程日记 2024/1/7 14:11:52

Winform中使用Websocket4Net实现Websocket客户端并定时存储接收数据到SQLite中

场景 SpringBootVue整合WebSocket实现前后端消息推送： SpringBootVue整合WebSocket实现前后端消息推送_websocket vue3.0 springboot 往客户端推送-CSDN博客 上面实现ws推送数据流程后，需要在windows上使用ws客户端定时记录收到的数据到文件中&#x…...

编程日记 2024/1/7 14:06:48

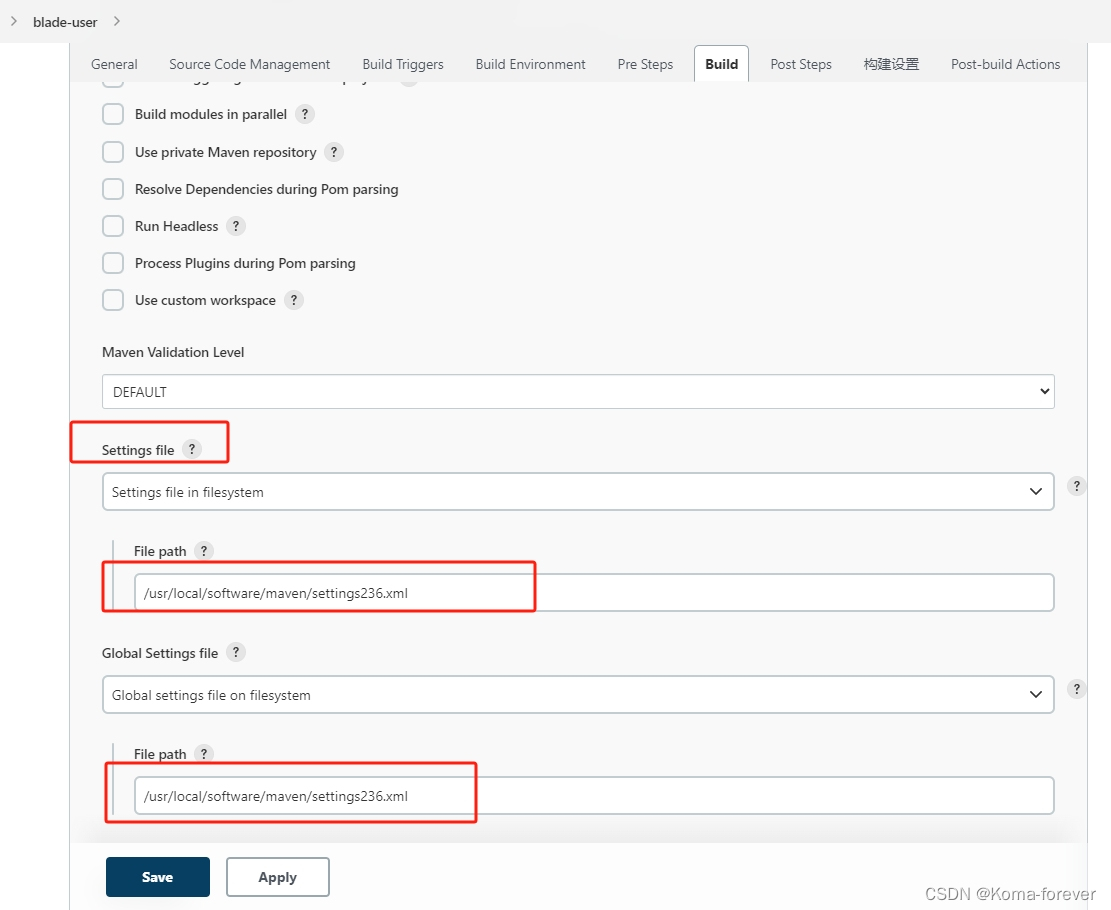
Jenkins修改全局maven配置后不生效解决办法、以及任务读取不同的settings.xml文件配置

一、修改Global Tool Configuration的maven配置不生效 说明：搭建好jenkins后，修改了全局的settings.xml，导致读取settings一直是之前配置的。 解决办法一 Jenkins在创建工作任务时，会读取当前配置文件内容，固定在这…...

编程日记 2024/1/7 14:05:47

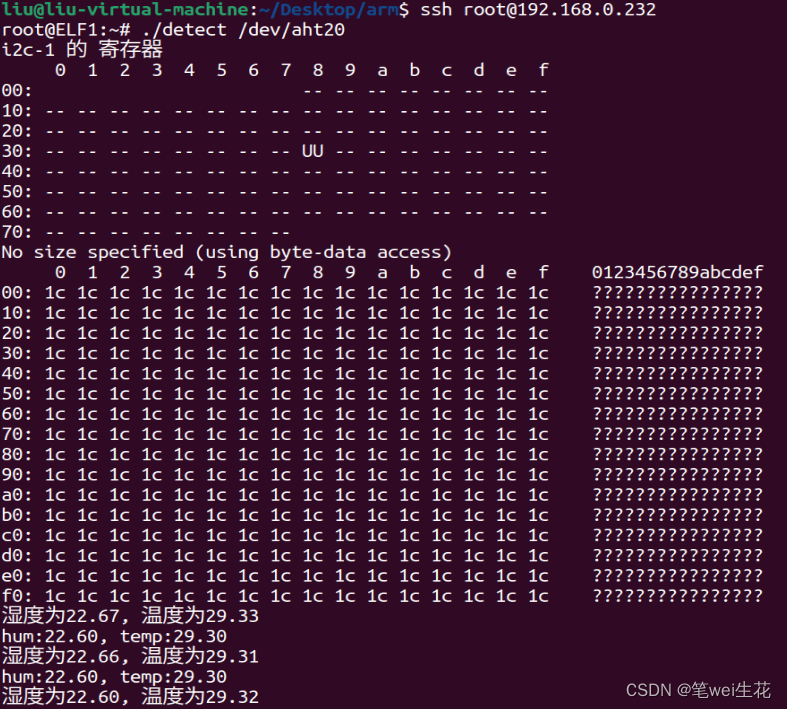
【elfboard linux开发板】7.i2C工具应用与aht20温湿度寄存器读取

1. I2C工具查看aht20的温湿度寄存器值 1.1 原理图 传感器通过IIC方式进行通信，连接的为IIC1总线，且设备地址为0x38，实际上通过后续iic工具查询，这个设备是挂载在iic-0上 1.2 I2C工具 通过i2c工具可以实现查询i2c总线、以及上面…...

编程日记 2024/1/7 14:02:44

LeetCode-有效的字母异位词（242）

题目描述： 给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。 注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。 思路： 这题还是比较简单的，首先将两个字符…...

编程日记 2024/1/7 14:01:43

【AIGC-图片生成视频系列-6】SSR-Encoder：用于主题驱动生成的通用编码器

目录 一. 贡献概述 二. 方法详解 a) 训练阶段 b) 推理生成阶段： 三. 综合结果 四. 注意力可视化 五. 选择性主题驱动图像生成 六. 人体图像生成 七. 可推广到视频生成模型 八. 论文 九. 个人思考 稳定扩散（Stable Diffusion）模型可…...

编程日记 2024/1/7 13:59:42

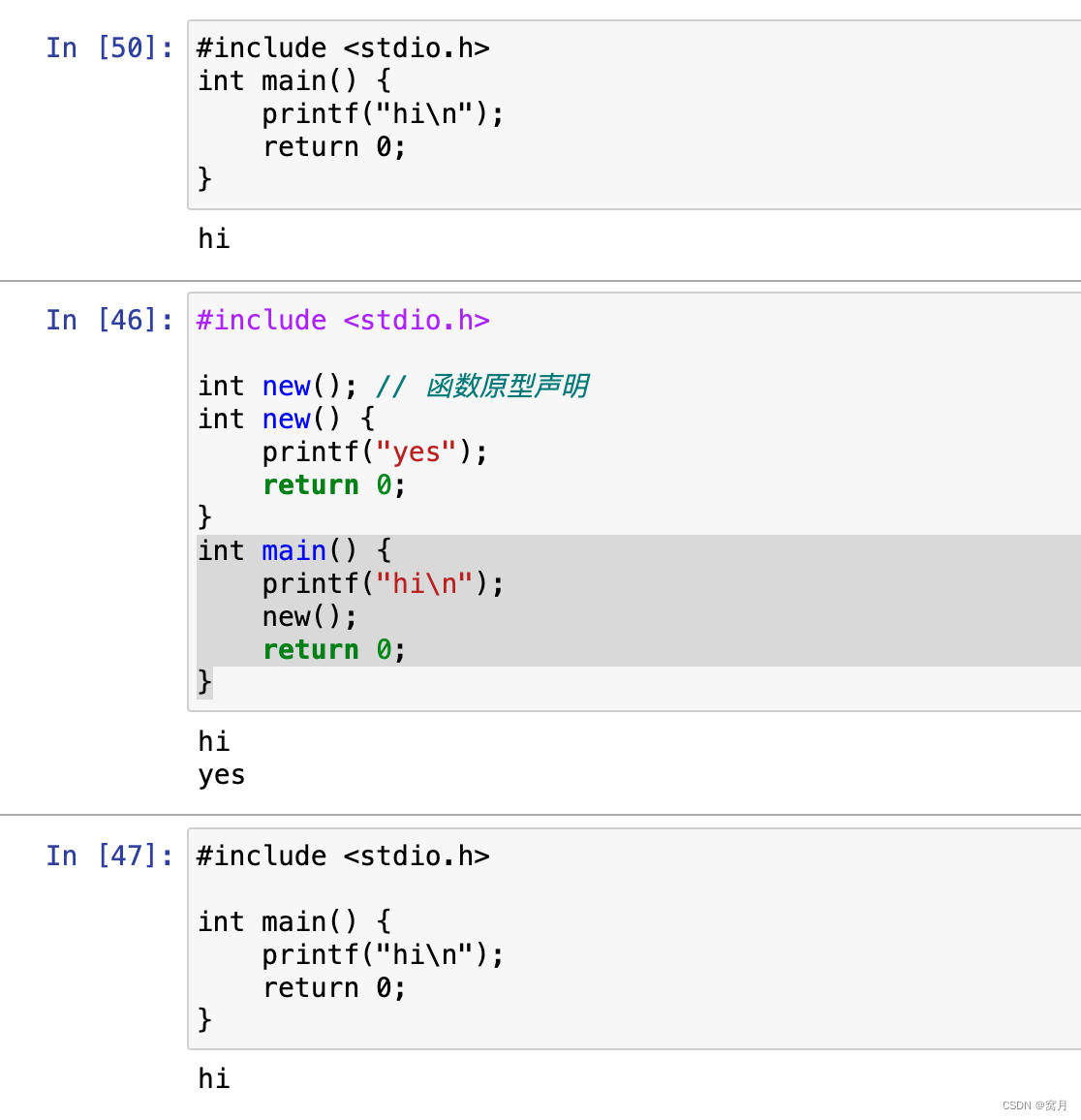
[C]jupyter中使用C

[C]jupyter中使用C 安装使用用处 安装 https://github.com/brendan-rius/jupyter-c-kernel 下拉找到3条命令，装就可以了 mac和linux可用 python3可用， 2不可以 第二条命令可以改为 : python3 install_c_kernel 小总结：如果有问题&#xff0…...

编程日记 2024/1/7 13:56:39

探讨一下WebINFO 下的一些思考

在平时的开发中，我们经常看到一个/WEB-INF 这个目录，这个是web 容器初始化加载的一个标准路径。官方解释：WEB-INF 是 Java 的 web 应用的安全目录。所谓安全就是客户端无法访问，只有服务端可以访问的目录。也就是说，这…...

编程日记 2024/1/7 13:55:38

MySQL中的开发基于Python的SQL工具类操作数据库简单示例

操作数据库封装SQL工具类的两种方式 为了更方便的实现基于连接池和pymysql 连接数据库，需开发一个sql工具类来让sql操作更简洁用两张方式来封装SQL工具类 1 ）单例模式 封装 db.py 工具类 import pymysql from dbutils.pooled_db import PooledDBclas…...

编程日记 2024/1/7 13:52:36

安卓Android Studio读写FM1208CPU卡源码

本示例使用的发卡器&#xff1a;https://item.taobao.com/item.htm?spma1z10.5-c-s.w4002-21818769070.11.6c46789elLwMzv&id615391857885 <?xml version"1.0" encoding"utf-8"?> <androidx.constraintlayout.widget.ConstraintLayout x…...

编程日记 2024/1/7 13:51:35

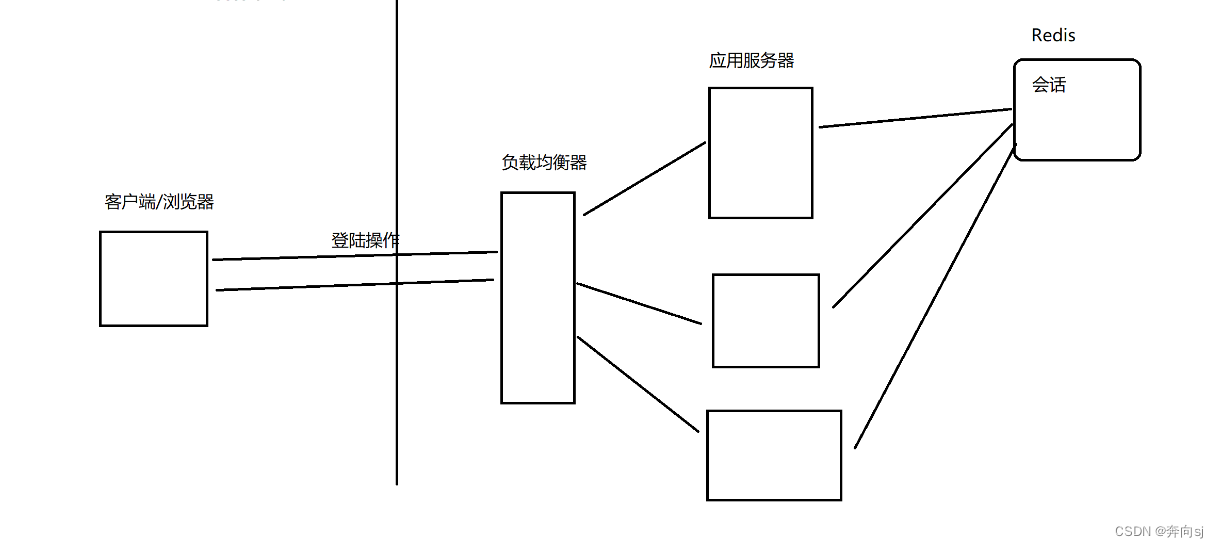
二、Redis的特性与应用场景

Redis是一个在内存中存储数据的中间件&#xff0c;主要用于作为数据库、数据缓存&#xff0c;在分布式系统中有着非常重要的地位。面试中可以围绕Redis的特性进行介绍。 一、Redis特性 1、在内存中存储数据 MySQL主要是“表”的方式来存储组织数据的&#xff0c;是“关系型数…...

编程日记 2024/1/7 13:43:27

编程笔记 html5cssjs 019 HTML实体

编程笔记 html5&css&js 019 HTML实体 一、HTML 字符实体二、HTML 符号实体小结 在HTML文档中&#xff0c;用一些标记表示特定的格式&#xff0c;那我们想使用这些标记字符本身时就出了问题&#xff0c;直接使用时&#xff0c;会被浏览器解析为标记的&#xff0c;要想显…...

编程日记 2024/1/7 13:39:22

数据结构：树详解

创建二叉树 给出了完整的先序遍历序列&#xff0c;子树为空用’#’表示&#xff0c;所以这样我们在通过先序遍历序列创建二叉树时我们直到先序遍历序列是先进行根结点&#xff0c;然后左子树最后右子树的顺序进行遍历的&#xff0c;所以对于完整的先序遍历序列我们可以直到先序…...

编程日记 2024/1/7 13:37:20

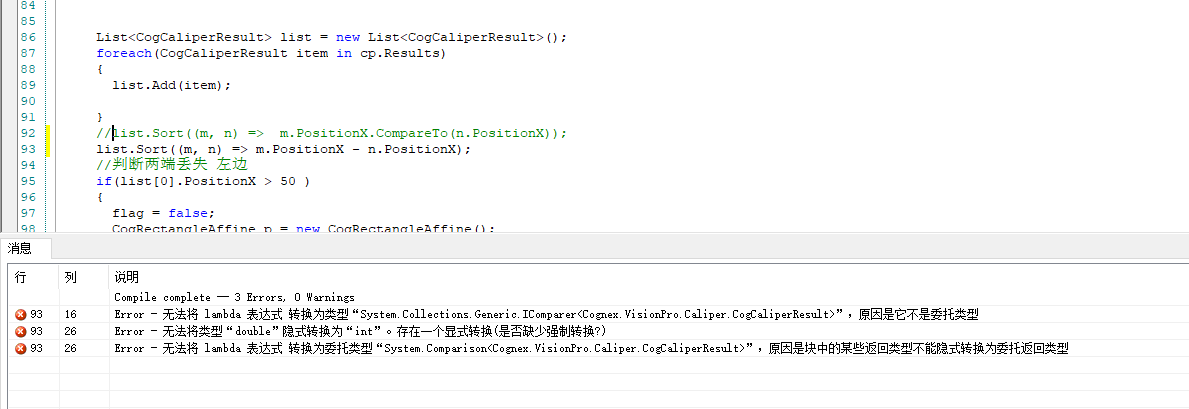
list1.Sort((m, n) =＞ m.Id - n.Id)； id是double类型的为什么回报错

问题产生的地方 原因 对于 double 类型的属性&#xff0c;不能直接使用减法运算符进行比较。减法运算符只能用于数值类型&#xff0c;而 double 是浮点数类型。 要在 double 属性上进行排序&#xff0c;可以使用 CompareTo 方法或者使用自定义的比较器。 更改 要在 double 属性…...

编程日记 2024/1/7 13:33:17

接口测试中缓存处理策略

在接口测试中&#xff0c;缓存处理策略是一个关键环节&#xff0c;直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性&#xff0c;避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明&#xff1a; 一、缓存处理的核…...

编程新知 2026/2/8 4:37:27

深度学习在微纳光子学中的应用

深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向&#xff1a; 逆向设计 通过神经网络快速预测微纳结构的光学响应&#xff0c;替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

编程新知 2026/2/7 4:19:43

conda相比python好处

Conda 作为 Python 的环境和包管理工具&#xff0c;相比原生 Python 生态&#xff08;如 pip 虚拟环境&#xff09;有许多独特优势&#xff0c;尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处&#xff1a; 一、一站式环境管理&#xff1a…...

编程新知 2025/11/29 6:54:19

树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频

使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源&#xff1a; http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

编程新知 2025/11/5 13:03:58

MySQL 隔离级别：脏读、幻读及不可重复读的原理与示例

一、MySQL 隔离级别 MySQL 提供了四种隔离级别，用于控制事务之间的并发访问以及数据的可见性，不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式，具体如下： 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交（READ UNCOMMITTED）允许出现允许…...

编程新知 2025/9/16 21:01:58

【项目实战】通过多模态+LangGraph实现PPT生成助手

PPT自动生成系统 基于LangGraph的PPT自动生成系统&#xff0c;可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析&#xff1a;自动解析Markdown文档结构PPT模板分析&#xff1a;分析PPT模板的布局和风格智能布局决策&#xff1a;匹配内容与合适的PPT布局自动…...

编程新知 2026/2/3 22:50:07

Frozen-Flask ：将 Flask 应用“冻结”为静态文件

Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是&#xff1a;将一个 Flask Web 应用生成成纯静态 HTML 文件&#xff0c;从而可以部署到静态网站托管服务上&#xff0c;如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

编程新知 2025/12/5 20:57:13

Neo4j 集群管理：原理、技术与最佳实践深度解析

Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档，本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石，用于构建高可用、可扩展且一致的图数据库服务…...

编程新知 2025/12/27 16:43:24

零基础在实践中学习网络安全-皮卡丘靶场（第九期-Unsafe Fileupload模块）（yakit方式）

本期内容并不是很难&#xff0c;相信大家会学的很愉快&#xff0c;当然对于有后端基础的朋友来说&#xff0c;本期内容更加容易了解&#xff0c;当然没有基础的也别担心&#xff0c;本期内容会详细解释有关内容 本期用到的软件&#xff1a;yakit&#xff08;因为经过之前好多期…...

编程新知 2026/1/21 12:29:04

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18