我的AI之旅开始了
知道重要,但是就是不动。
今天告诉自己,必须开始学习了。
用这篇博文作为1月份AI学习之旅的起跑点吧。
从此,无惧AI,无惧编程。
AI之路就在脚下。
AI,在我理解,就是让机器变得更加智能,能够以人思考和行为的方式去实行某种操作,更大更快更强。
编程和AI的关系,就如同鱼与水的关系。
没有编程,AI就没有办法乖乖的听我们的话,做我们要它做的事。
编程,就相当于是发布一条条指令,指挥机器去干这个,去干那个。
机器就是一堆机械堆砌出来的玩意。他们没有感情,只会冷血的一条一条执行程序。
想让它为我所用,就得学编程。
所以,MATLAB,我来了。
反向学习:

利用反向学习,可以增加种群的多样性,防止种群陷入局部最优。
基本初等函数:
正弦、余弦、反正弦、反余弦、正切、余切、反正切、反余切、指数、对数、幂、以e为底的指数函数、S型函数等。
这些基本初等函数可以两两组队成为复合函数。
高斯随机游走策略:
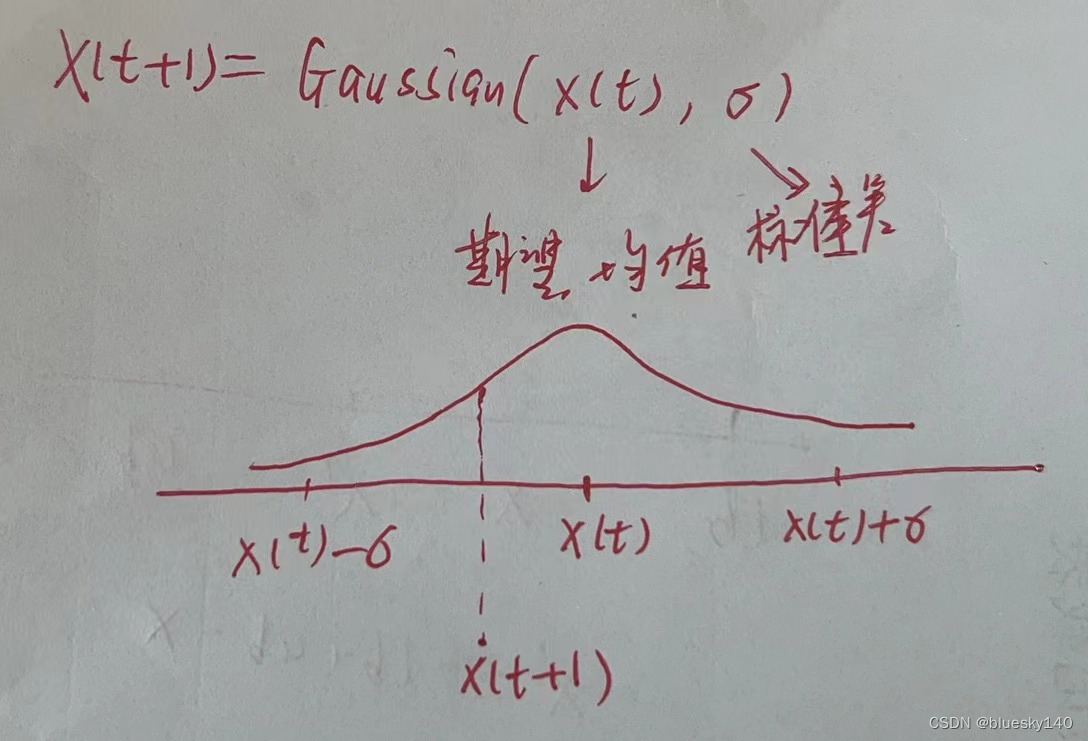
下一步位置等于上一步位置的高斯扰动。
在上一个位置的基础上,下一个位置存在于距离上一个位置左右两边距离标准差σ内存在的可能性比较大。
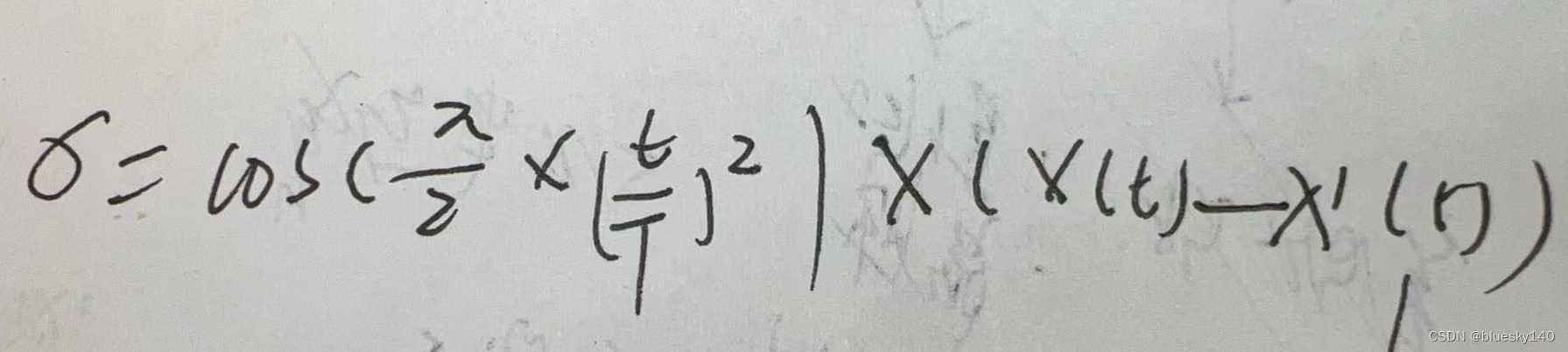
x'(t)表示最佳位置,或者平均位置,或者中位数位置。
高斯分布,也可以改成柯西分布,或者莱维分布。
1、2、5、9、13的中位数为5。
通过余弦函数,在迭代前期施加较大扰动,在迭代后期,扰动迅速减小,进而平衡了算法的探索和开发能力。
方差和标准差:
1、正负1倍标准偏差的概率 =68.3%;
2、正负2倍标准偏差的概率 =95.5%;
3、正负3倍标准偏差的概率 =99.7%;
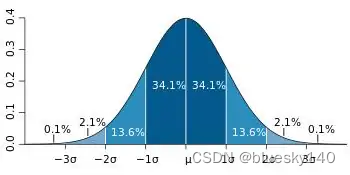
标准差(standard deviation)
标准差是一组数值自平均值分散程度的一种测量观念。

一个较大的标准差,代表大部分的数值和其平均值之间差异较大,一个较小的标准差,代表这些数值较接近平均值。
例如:
两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是7,但第二个集合具有较小的标准差
标准差应用于投资上,可作为量度回报稳定性的指标。标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。相反,标准差数值越小,代表回报较为稳定,风险亦较小。
例如:
A,B两组各有6位学生参加同一次语文测验,A组的分数为95,85,75,65,55,45
B组的分数为73,72,71,69,68,67
这两组的平均数都是70,但A组的标准差为17.078分,B组的标准差为2.160分,说明A组学生之间的差距要比B组学生之间的差距大得多
上面的靶上有两套落点。尽管两套落点的平均中心位置都在原点 (即期望相同),但两套落点的离散程度明显有区别。蓝色的点离散程度更小。
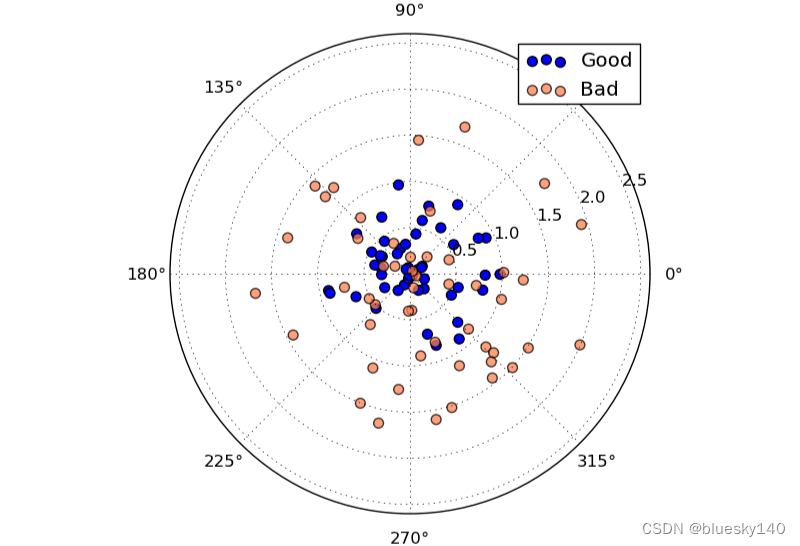
方差(variance):
数学上,我们用方差来代表一组数据或者某个概率分布的离散程度。可见,方差是独立于期望的另一个对分布的度量。两个分布,完全可能有相同的期望,而方差不同,正如我们上面的箭靶。

标准差和方差的关系为:

搜索文章顺序:标题-主题-全文
惯性权重总是和位置联系在一起,在其它地方就叫调整因子、惯性因子、权重因子、收缩策略等。
初始化
惯性因子
位置更新1或2个。全局一个,局部一个。
E
朋友说的话:引导直播预约,钩子引导私域,不浪费每一个流量价值。
地上本没有坑,拿铲子挖出坑来。
相关文章:

我的AI之旅开始了
知道重要,但是就是不动。 今天告诉自己,必须开始学习了。 用这篇博文作为1月份AI学习之旅的起跑点吧。 从此,无惧AI,无惧编程。 AI之路就在脚下。 AI,在我理解,就是让机器变得更加智能&#…...

Day25 235二叉搜索树的公共祖先 701二叉搜索树插入 450二叉搜索树删除
235 二叉搜索树的最近公共祖先 如果利用普通二叉树的方法,就是利用后序遍历回溯从低向上搜索,遇到左子树有p,右子树有q,那么当前结点就是最近公共祖先。本题是二叉搜索树,所以说是有序的,一定能够简化上面…...

android系列-init 挂载文件系统
1.init 挂载文件系统 //android10\system\core\init\main.cppint main(int argc, char** argv) {return FirstStageMain(argc, argv); } //android10\system\core\init\first_stage_init.cppint FirstStageMain(int argc, char** argv) {CHECKCALL(mount("tmpfs",…...

Spring 七种事务传播性介绍
作者:vivo 互联网服务器团队 - Zhou Shaobin 本文主要介绍了Spring事务传播性的相关知识。 Spring中定义了7种事务传播性: PROPAGATION_REQUIRED PROPAGATION_SUPPORTS PROPAGATION_MANDATORY PROPAGATION_REQUIRES_NEW PROPAGATION_NOT_SUPPORTED…...

Count the Colors ZOJ - 1610
题目链接 题意: 给定n个区间[ l, r ]和颜色c, 每次给[l, r]涂上c这个颜色. 后面的涂色会覆盖之前的涂色. 最后要求输出区间[0, 8000]中每种颜色及其出现的次数, 如果该颜色没有出现过则不输出. 思路:典型的线段树区间染色问题,一般这种题…...

MATLAB点云处理总目录
一、点云滤波 原始点云包含过多噪点和冗余点,滤波和采样往往是点云预处理的必要步骤 1.滤波 重复点去除 NAN或INF无效点去除 自定义半径滤波 2.采样 基于空间格网的点云抽稀 随机下采样 均匀体素下采样 非均匀体素下采样 二、邻近搜索 如何组织点云快速获取当前…...

C语言逗号表达式如何计算
在 C 语言中,逗号表达式是一种特殊的表达式形式,它由逗号分隔的多个表达式组成。 逗号表达式的计算过程如下:1、从左到右依次计算每个表达式的值。2、最终返回的值是最右边表达式的值。3、逗号表达式的求值过程是顺序执行的,不会…...
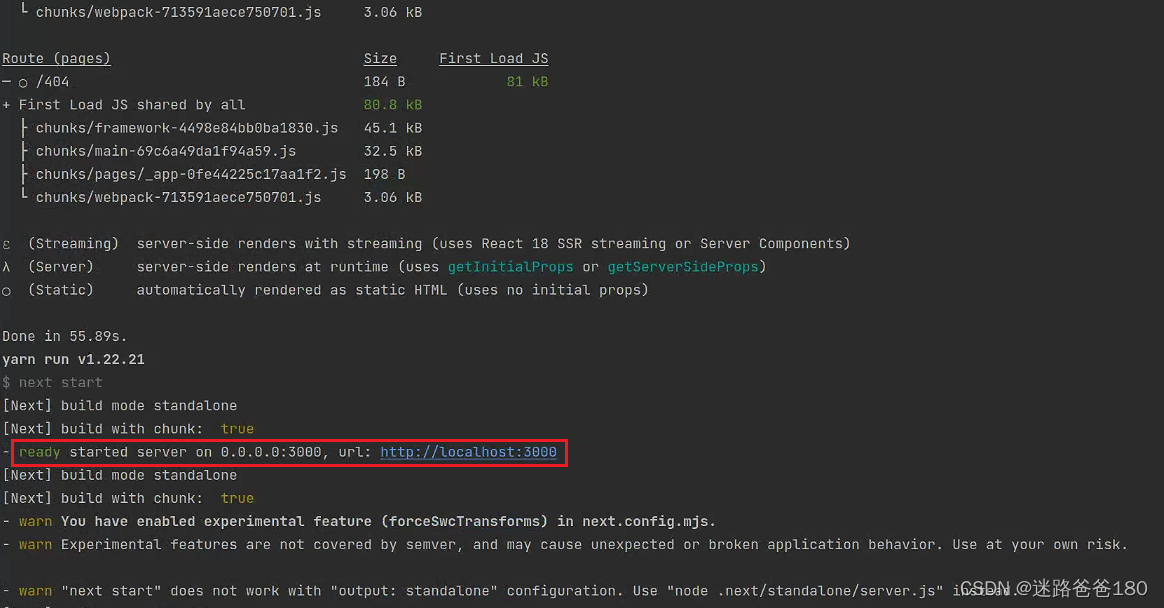
Ubuntu 本地部署 ChatGPT-Next-Web
Ubuntu 本地部署 ChatGPT-Next-Web 文章目录 Ubuntu 本地部署 ChatGPT-Next-Web ChatGPT-Next-Web 项目地址:https://github.com/ChatGPTNextWeb/ChatGPT-Next-Web 本文主要演示如何在 Ubuntu 本地(默认是端口 3000)部署 ChatGPT-Next-Web&am…...
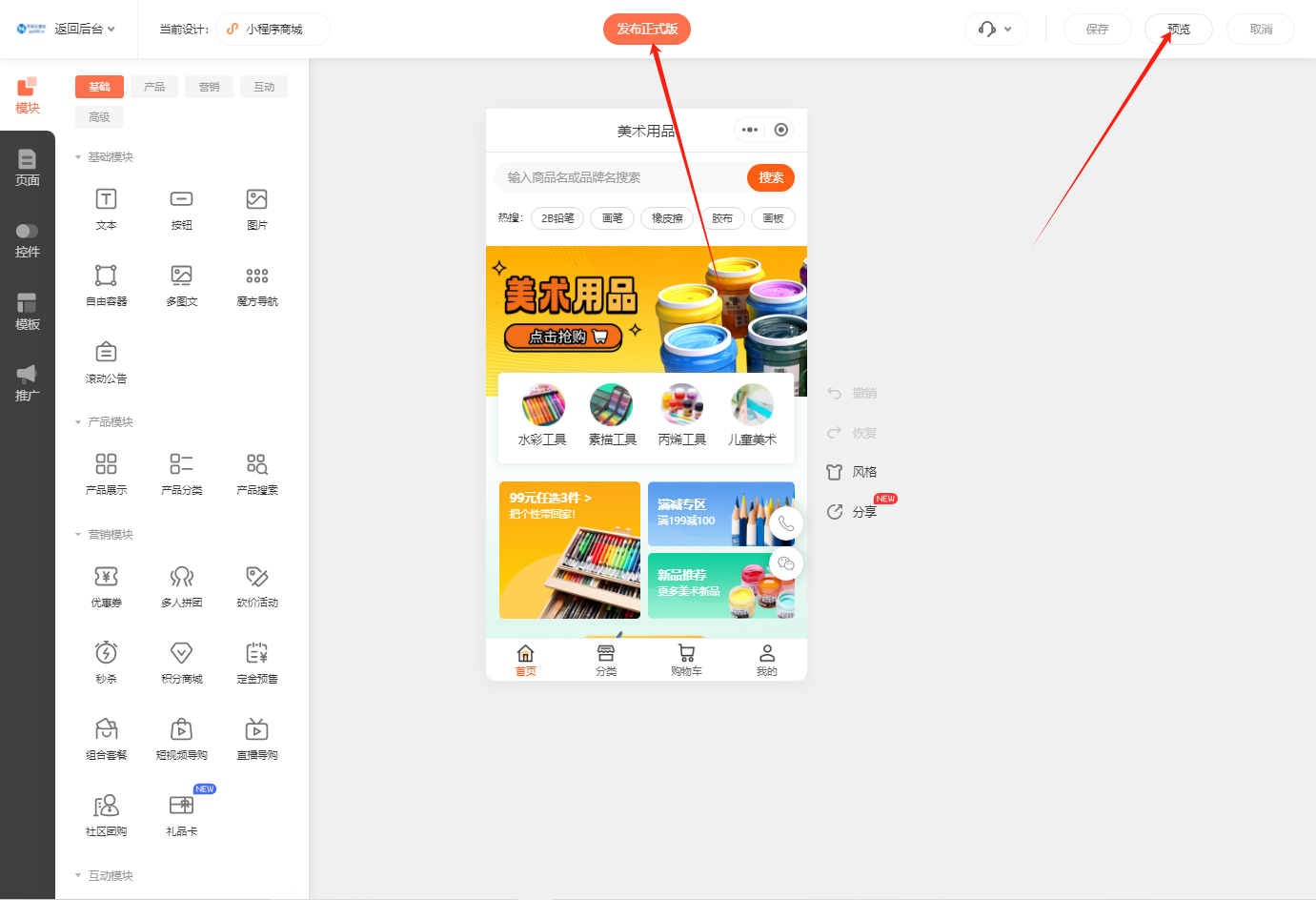
小程序商城搭建:快速入门指南
随着移动互联网的普及,小程序商城逐渐成为了商家们进行线上销售的重要渠道。如果你也想搭建一个小程序商城,那么本文将为你介绍如何使用乔拓云这一第三方小程序搭建平台来轻松搭建自己的小程序商城。 一、选择合适的第三方小程序搭建平台 在选择第三方小…...
c# windows10大小端试
测试代码: unsafe public void ceshi() {byte[] by BitConverter.GetBytes(0x12345678);Debug.WriteLine(" byte[0] 0x" by[0].ToString("x2"));Debug.WriteLine(" byte[1] 0x" by[1].ToString("x2"));Debug.WriteLi…...

【算法专题】动态规划之斐波那契数列模型
动态规划1.0 动态规划 - - - 斐波那契数列模型1. 第 N 个泰波那契数2. 三步问题3. 使用最小花费爬楼梯4. 解码方法 动态规划 - - - 斐波那契数列模型 1. 第 N 个泰波那契数 题目链接 -> Leetcode -1137. 第 N 个泰波那契数 Leetcode -1137. 第 N 个泰波那契数 题目&…...
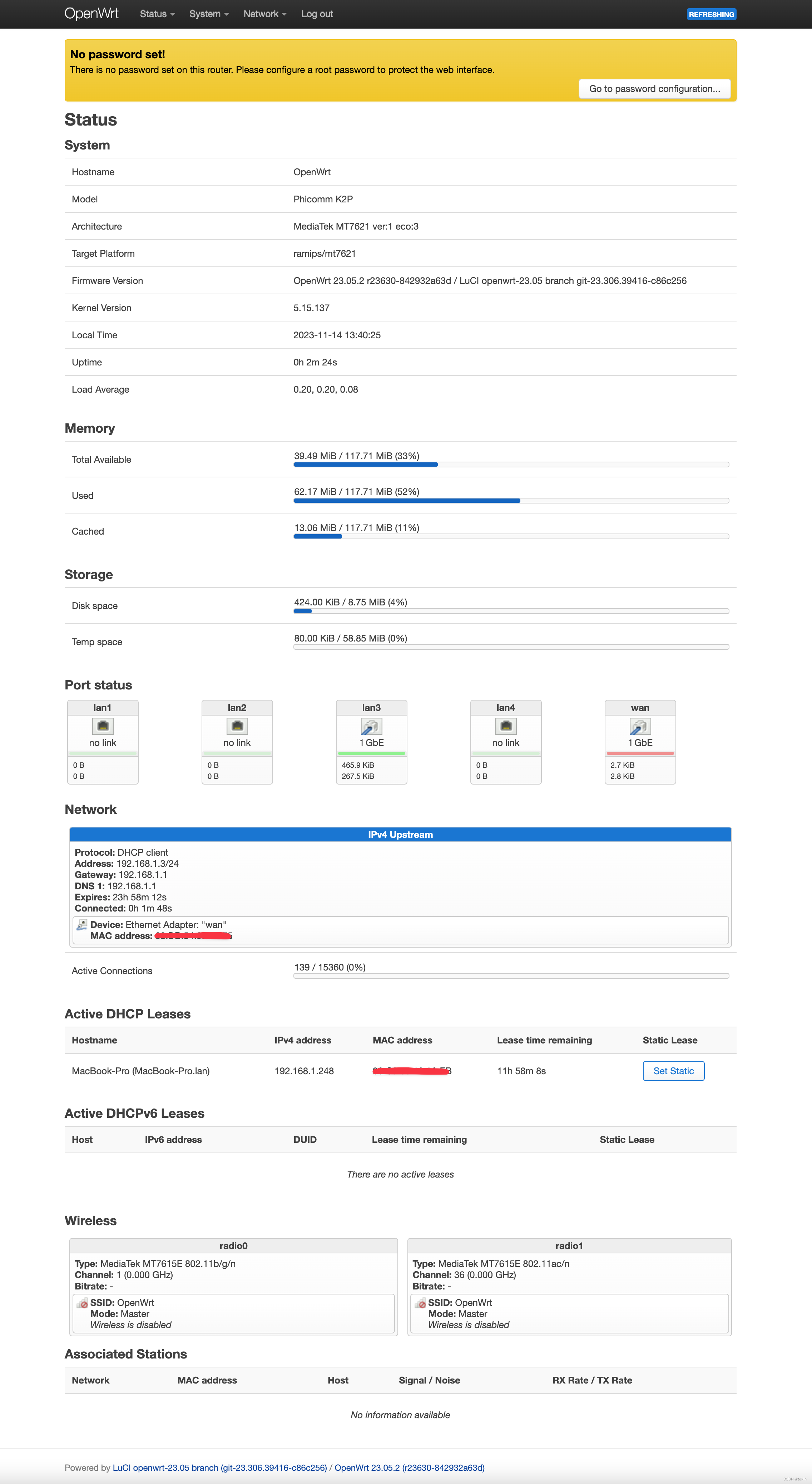
K2P路由器刷OpenWrt官方最新版本固件OpenWrt 23.05.2方法 其他型号的智能路由器OpenWrt固件刷入方法也基本上适用
最近路由器在开机时总出问题,于是就那他来开刀,直接刷一个OpenWrt官方最新版本的固件, 刷其他第三方的固件总是觉得不安全, 而且很多第三方固件都带了些小工具,始终会有安全隐患, 而且占用内存空间太多,本来这个东西就没有多少内存,于是就干脆刷一个官方的原始固件(才6.3M, 相…...

AI大语言模型会带来了新一波人工智能浪潮?
以ChatGPT、LLaMA、Gemini、DALLE、Midjourney、Stable Diffusion、星火大模型、文心一言、千问为代表AI大语言模型带来了新一波人工智能浪潮,可以面向科研选题、思维导图、数据清洗、统计分析、高级编程、代码调试、算法学习、论文检索、写作、翻译、润色、文献辅助…...

How to view the high-tech zone atmospheric project
How to view the high-tech zone atmospheric project 问题与建议登录界面没有验证码部分页面加载时间过长联动型下拉列表框点击反应迟钝页面缺乏导航没有采用https协议没有完成域名实名认证左侧菜单区不能收缩大屏区域功能图层不能完全隐藏部分页面表单控件没有文案提示其功能…...

sqlalchemy 中的缓存机制解释
SQLAlchemy 的缓存机制主要涉及两个层面:会话(Session)缓存和查询缓存。这两种缓存机制对于提升应用性能和数据一致性都非常重要。下面详细解释这两种缓存机制: 1. 会话(Session)缓存 会话缓存是 SQLAlch…...
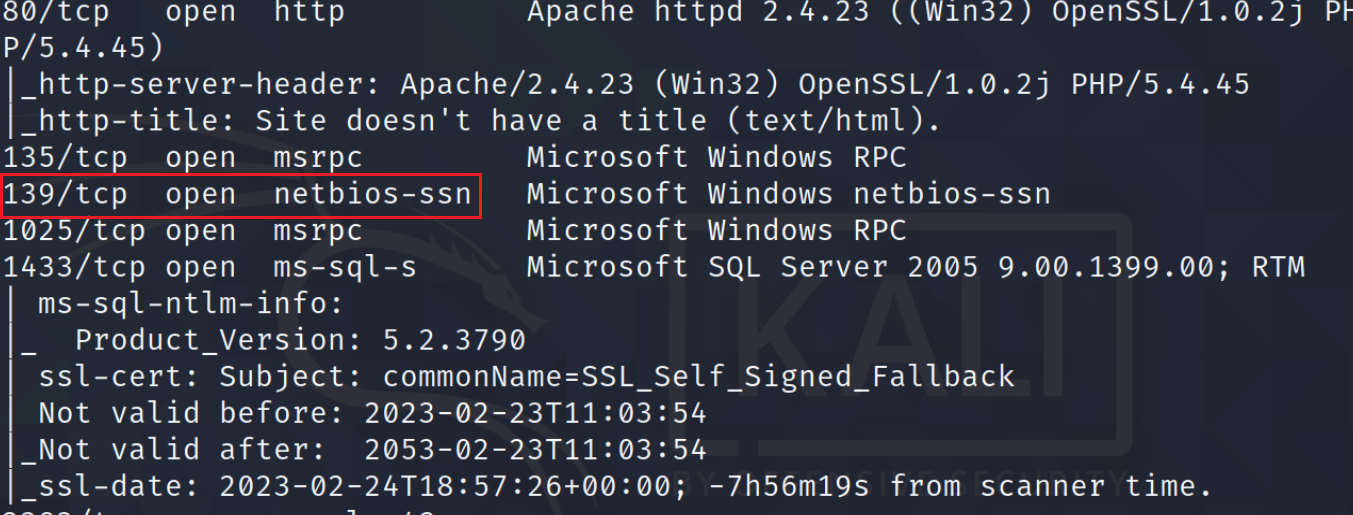
网络安全B模块(笔记详解)- 漏洞扫描与利用
漏洞扫描与利用 1.通过Kali对服务器场景server2003以半开放式不进行ping的扫描方式并配合a,要求扫描信息输出格式为xml文件格式,从生成扫描结果获取局域网(例如172.16.101.0/24)中存活靶机,以xml格式向指定文件输出信息(使用工具Nmap,使用必须要使用的参数),并将该操…...
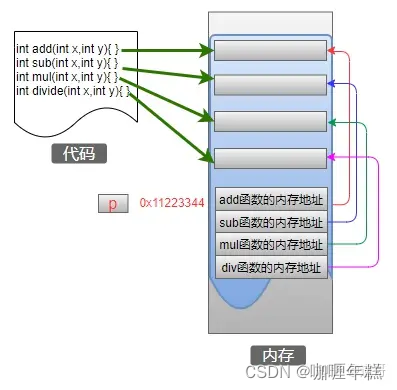
【C语言】指针——从底层原理到应用
C语言指针-从底层原理到花式技巧,用图文和代码帮你讲解透彻 目录 一、前言二、变量与指针的本质 1. 内存地址2. 32位与64位系统3. 变量4. 指针变量5. 操作指针变量 5.1 指针变量自身的值5.2 获取指针变量所指向的数据5.3 以什么样的数据类型来使用/解释指针变量所指…...

想了解步进伺服的朋友可以了解下这个方案
TMC4361A 是一款小型化、高性能的驱动步进电机的运动控制器。实用于很多的斜坡轮廓的应用,特别是速度快、限制过冲的运动场合。用户根据自己的要求实现 S 形或 sixPoint™六点式速度轮廓配置及闭环或开环的操作、动态修改运动参数。TMC4361A 包含 SPI接口、Step/Dir…...

航天航空线束工艺3D虚拟展馆支持多人异地参观漫游
为了满足汽车线束企业员工工作需要,让新老员工了解到更先进、规范的线束工艺设计技术,华锐视点基于VR虚拟仿真、web3d开发和图形图像技术制作了一款汽车线束工艺设计VR虚拟仿真模拟展示系统。 汽车线束工艺设计VR虚拟仿真模拟展示系统共分为pc电脑端和VR…...
JAVA面向对象基础-容器
一、泛型 我们可以在类的声明处增加泛型列表,如:<T,E,V>。 此处,字符可以是任何标识符,一般采用这3个字母。 【示例9-1】泛型类的声明 1 2 3 4 5 6 7 8 9 10 class MyCollection<E> {// E:表示泛型; Object[] o…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
