【算法每日一练]-动态规划 (保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔
目录
今日知识点:
计算最长子序列的方案个数,类似最短路径个数问题
四柱河内塔问题:dp[i]=min{ (p[i-k]+f[k])+dp[i-k] }
纸带
围栏木桩
四柱河内塔
纸带

思路:
我们先设置dp[i]表示从i到n的方案数。
那么减法操作中:i可以移动到[1,i-1]中的任意一个格子。反过来可以认为:i可以从i+1到n转移过来。所以得出dp[i]=dp[i+1]+…dp[n];(使用后缀和即可)
然后除法操作中:i可以移动到[1,i/2]中的任意一个格子。反过来可以认为:i可以从x/2==i的任意x移动过来。所以得出dp[i]+=sum[i*j]-sum[i*j+j](i*j<=n)
#include <bits/stdc++.h>
using namespace std;
const int N=4e6+5;
int n,mod,dp[N],sum[N];int main(){cin>>n>>mod;dp[n]=sum[n]=1;for(int i=n-1;i>=1;i--){dp[i]=sum[i+1];//减法for(int j=2;j*i<=n;j++){//除法int r=min(n,i*j+j-1);dp[i]=(dp[i]+sum[i*j]-sum[r+1])%mod;}sum[i]=(sum[i+1]+dp[i])%mod;} cout<<dp[1];
}
围栏木桩

输入:
3
9 10 1 9 8 7 6 3 4 6
3 100 70 102
6 40 37 23 89 91 12
思路:
其实就是先找最长上升子序列,然后再求有多少个最长的上升子序列。
首先设置dp[i]表示以i结尾的最长上升子序列。
转移:(i能拼在j后面的话)dp[i]=max(dp[j])+1;
那么要求有多少个最长上升子序列的话就要进行修改,
把dp[i]=max(dp[j])+1改成 if(dp[j]+1>dp[i]) dp[i]=dp[j]+1;
这样的话就能知道什么时候修改了dp[i],当修改dp[i]的时候自然是因为i可以拼在j之后且拼完后dp[i]会变大。
故:f[i]=f[j]
当dp[j]+1=dp[i]时候,说明i即便拼在j后面dp也不会变化,那就说明拼在这个j后面也是最优解。
故:f[i]+=f[j]
类似最短路径个数问题嘛!
#include <bits/stdc++.h>
using namespace std;
const int N=27;
int n,m,h[N],dp[N],f[N],ans1,ans2;int main(){cin>>m;while(m--){cin>>n;ans1=0;ans2=0;for(int i=1;i<=n;i++){cin>>h[i];dp[i]=f[i]=1;}for(int i=2;i<=n;i++)for(int j=i-1;j;j--){if(h[j]<=h[i]){if(dp[j]+1>dp[i]){//更新最优解就继承dp[i]=dp[j]+1;f[i]=f[j];}else if(dp[j]+1==dp[i])//当前的j也是可以使变成最优解的jf[i]+=f[j];}}for(int i=1;i<=n;i++)ans1=max(ans1,dp[i]);for(int i=1;i<=n;i++)if(dp[i]==ans1)ans2+=f[i];cout<<ans1<<" "<<ans2<<'\n';}
}
四柱河内塔

思路:
这道题听过的很简单,没见过的确实很难做了。
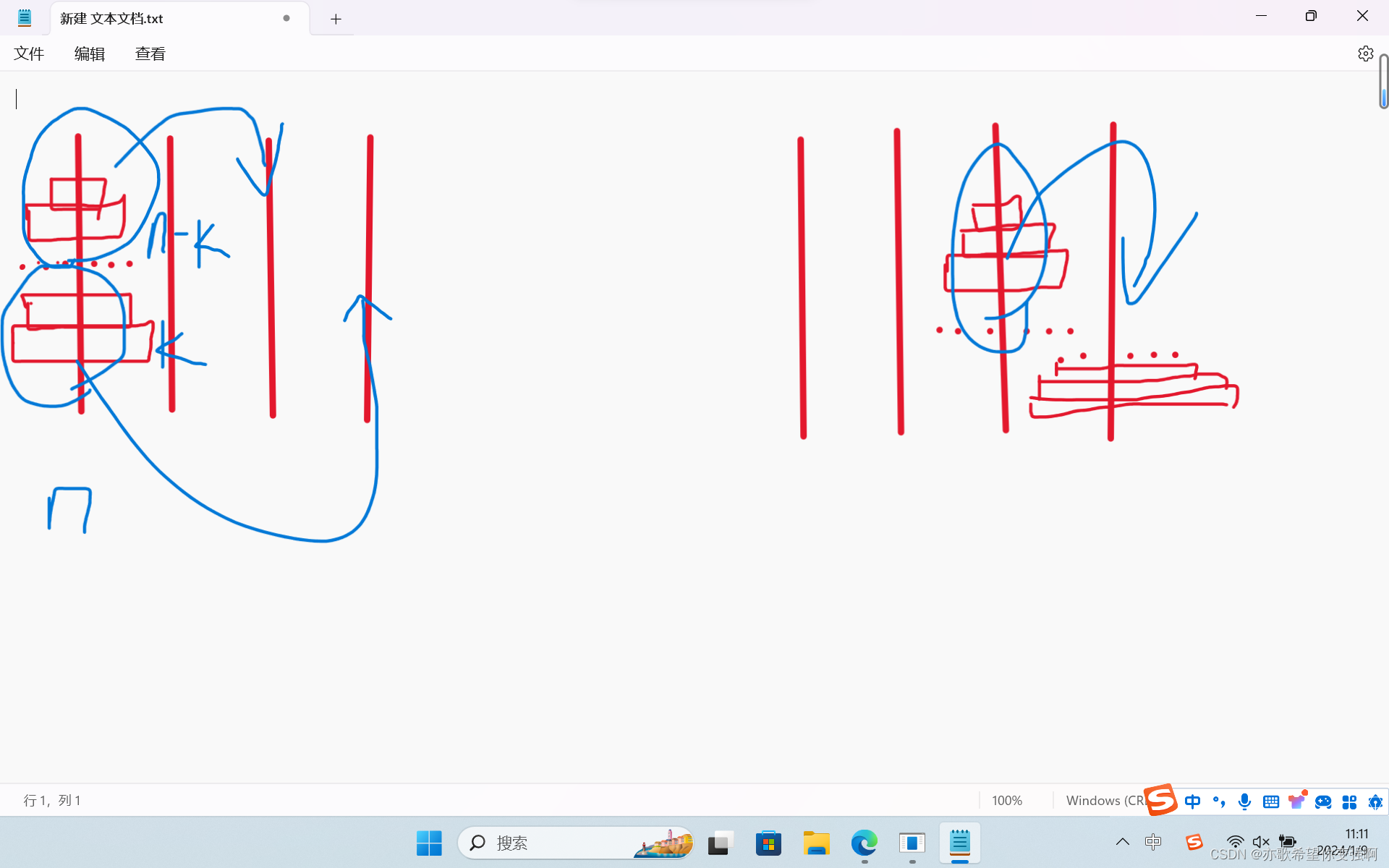
首先我们从最简单的3柱开始:就如下图,对于n柱的河内塔把第一柱上面n-1个放到中间的柱子上,然后剩下的一个放到最右边,然后就转化成了把n-1个盘子的三柱河内塔问题。
设置dp[i]表示i个盘子的三柱河内塔问题。
那么对应转移方程:dp[i]=(dp[i-1]+1)+dp[i-1]=2*dp[i-1]+1

那么现在来考虑四柱河内塔情况:
对于n个盘子的四柱河内塔,我们先将上面的n-k个放到任意一柱上,然后剩余的k个放到最右边柱子。最后也转化成了n-k个盘子的四柱河内塔问题。
要注意的一点是:在转移k个盘子的情况属于3柱的河内塔问题,因为有一柱是不能使用的。
转移方程:dp[i]=(p[i-k]+f[k])+dp[i-k] 其中f[k]是三柱k个盘子的河内塔问题。dp[i-k]是四柱n-k个盘子的河内塔问题。但是我们并不确定到底是让k取多少,但是我们确定的是k的选值必须使得dp[i]最小。那么就有dp[i]=min{ (p[i-k]+f[k])+dp[i-k] }
下面是代码部分
#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
int f,dp[55];
int main(){cin>>f;memset(dp,INF,sizeof(dp));dp[0]=0;dp[1]=1;dp[2]=3;//初始化cout<<1<<'\n'<<3<<'\n';for(int i=3;i<=f;i++){for(int j=1;j<i;j++){if(dp[i]>2*dp[i-j]+pow(2,j)-1)//pow(2,j)-1就是f[j]的值dp[i]=2*dp[i-j]+pow(2,j)-1;}cout<<dp[i]<<'\n';}
}
相关文章:

【算法每日一练]-动态规划 (保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔
目录 今日知识点: 计算最长子序列的方案个数,类似最短路径个数问题 四柱河内塔问题:dp[i]min{ (p[i-k]f[k])dp[i-k] } 纸带 围栏木桩 四柱河内塔 纸带 思路: 我们先设置dp[i]表示从i到n的方案数。 那么减法操作中ÿ…...

Grounding 模型 + SAM 报错
引入 Grounding 目标检测模型串联 SAM 从而实现实例分割任务,目前支持 Grounding DINO 和 GLIP 参考教程 MMDetection-SAM 如果是 Grounding DINO 则安装如下依赖即可 cd playground pip install githttps://github.com/facebookresearch/segment-anything.git pip…...
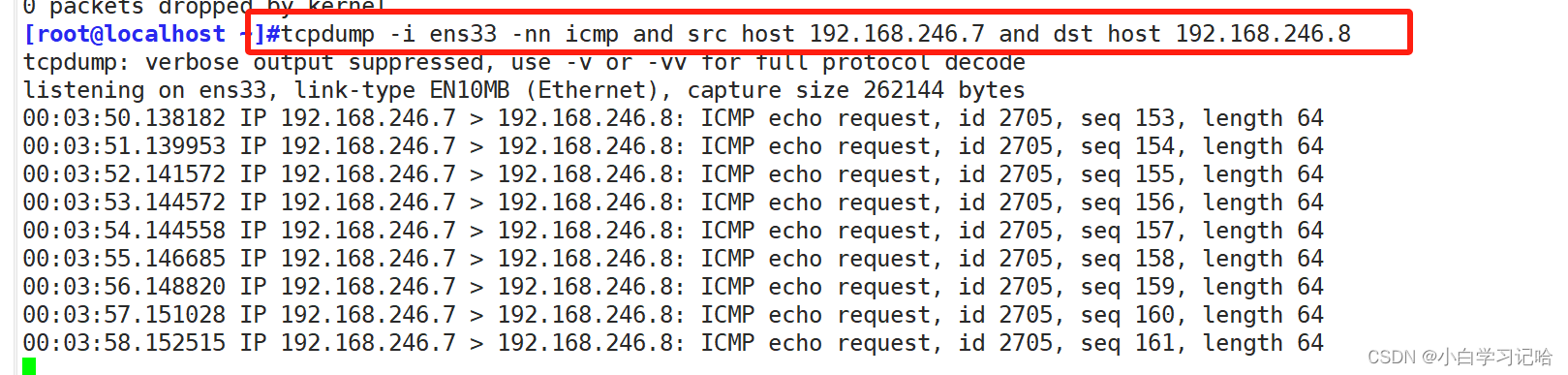
linux 网络基础配置
将Linux主机接入到网络,需要配置网络相关设置一般包括如下内容: 主机名 iP/netmask (ip地址,网关) 路由:默认网关 网络连接状态 DNS服务器 (主DNS服务器 次DNS服务器 第三个DNS服务器) 一、…...

leetcode-相同的树
100. 相同的树 使用递归的方法 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.right right class Solution:def isSameTree(self, p: …...
)
Leetcode17-好数对的数目(1512)
1、题目 给你一个整数数组 nums 。 如果一组数字 (i,j) 满足 nums[i] nums[j] 且 i < j ,就可以认为这是一组 好数对 。 返回好数对的数目。 示例 1: 输入:nums [1,2,3,1,1,3] 输出:4 解释:有 4 组好数对&am…...
Ubuntu22.04开机左上角下划线闪烁不开机
按下CtrlAltF2,打开TTY系统,然后通过用户名和密码登录,随后使用 sudo apt --fix-broken install 根据提示排除错误信息,然后使用apt安装lightdm安装就行。 tips:当使用EasyConnect的时候,你可能参考了下面这篇文章知…...

提升测试多样性,揭秘Pytest插件pytest-randomly
大家可能知道在Pytest测试生态中,插件扮演着不可或缺的角色,为开发者提供了丰富的功能和工具。其中,pytest-randomly 插件以其能够引入随机性的特性而备受欢迎。本文将深入探讨 pytest-randomly 插件的应用,以及如何通过引入随机性…...
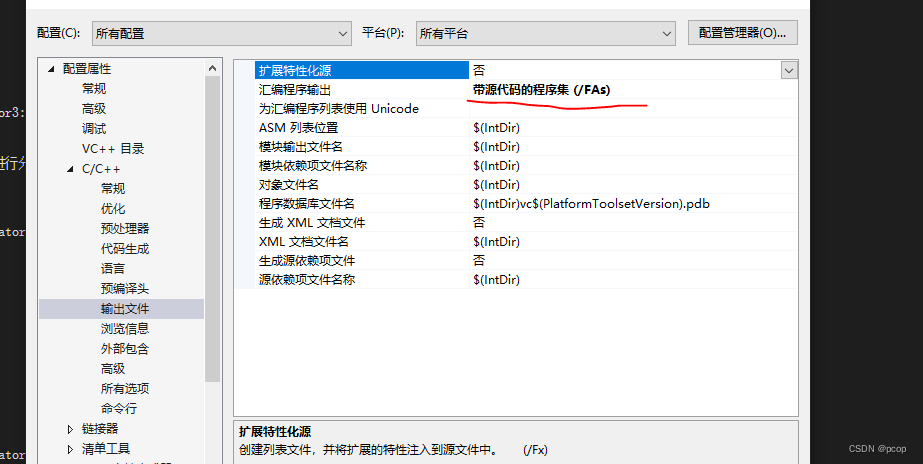
C++学习笔记(三十二):c++ 堆内存与栈内存比较
本节对堆和栈内存进行描述。 应用程序启动后,操作系统将整个程序加载到内存,分配相应的物理ram,确保程序可以正常运行。堆和栈是ram中存在的两个区域。栈通常是一个预定义大小的内存区域,一般是2M字节左右。堆也是预定了默认值的…...

探索Shadowsocks-Android:保护你的网络隐私
探索Shadowsocks-Android:保护你的网络隐私 I. 引言 在数字时代,网络隐私和安全变得愈发重要。我们越来越依赖互联网,但同时也面临着各种网络限制和监控。在这个背景下,Shadowsocks-Android应用程序应运而生,为用户提…...

蓝桥杯练习题(二)
📑前言 本文主要是【算法】——蓝桥杯练习题(二)的文章,如果有什么需要改进的地方还请大佬指出⛺️ 🎬作者简介:大家好,我是听风与他🥇 ☁️博客首页:CSDN主页听风与他 …...

将文本文件导入Oracle数据库的简便方法:SQL Developer
需求 我有一个文本文件dbim.txt,是通过alert log生成的,内容如下: 2020-09-11 2020-09-11 ... 2023-12-03 2023-12-03 2023-12-26我已经在Oracle数据库中建立了目标表: create table dbim(a varchar(16));我想把日志文件导入Or…...

Mac iTerm2 配置
Mac iTerm2 配置 安装 brew install iTerm2安装完成之后,需要重新打开终端,既可以看见安装 iTerm2 的效果。 iTerm2 美化 使用 oh-my-zsh 美化 iTerm2 终端 安装 brew install wget sh -c "$(wget https://raw.github.com/ohmyzsh/ohmyzsh/mast…...
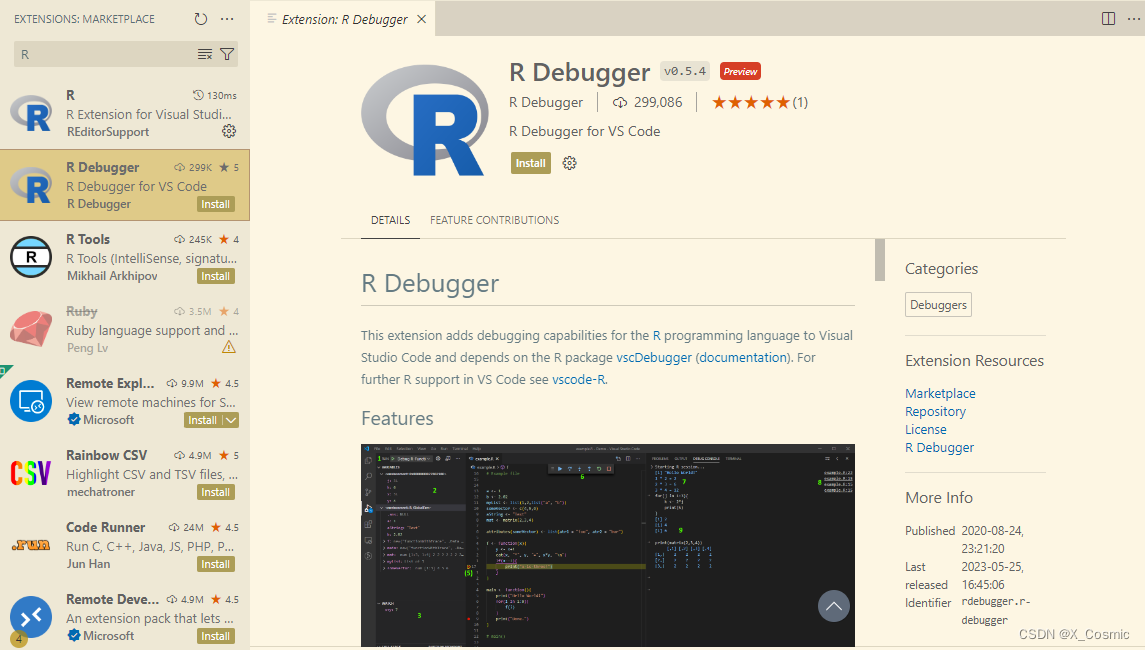
R语言下载安装及VScode配置
文章目录 1. R 下载和安装1.1 下载1.2 安装 2. VSCODE 配置2.1 安装R拓展2.2 安装R语言辅助功能包2.3 DEBUG 1. R 下载和安装 1.1 下载 网址:https://www.r-project.org/ 选择一个镜像地址下载 选择对应的版本 一般选择base即可 1.2 安装 下载安装包后按提示安装…...

【hyperledger-fabric】部署Java应用远程访问智能合约
简介 首先是根据b站的视频 hyperledger-fabric【3】在 java 应用中访问合约 以及hyperledger-fabric【5】Java应用和私有数据,本文章主要讲述的是视频中我遇到的问题,以及相关知识点的总结。 遇到的问题 问题1:git clone下载下来的代码发现…...
SpringBoot 调用mybatis报错:Invalid bound statement (not found):
启动SpringBoot报错:Invalid bound statement (not found): 参考此文排查 命中了第6条 记录一手坑爹的Invalid bound statement (not found)(六个方面) mapper文件路径配置错误 订正以后 问题解决...

PHP开发日志 ━━ 不同方法判断某个数组中是否存在指定的键名,测试哪种方法效率高
我们可以用isset($arr[a]) 或者 array_key_exists(a, $arr) 来判断a键名是否存在与$arr数组。 那么这两种方式哪个运行速度快呢? 不多废话了,现在我们写一段代码来测试一下: $array [a > 1, b > 2, c > 3];$start microtime(tru…...
【pytorch学习】 深度学习 教程 and 实战
pytorch编程实战博主:https://github.com/lucidrains https://github.com/lucidrains/vit-pytorch...
的实现方法)
js中和Vue中的事件委托(事件代理)的实现方法
目录 一、事件委托(事件代理) 1、事件委托的优点 2、事件委托的缺点 3、为什么要使用事件委托 4、事件委托实现原理 5、DOM事件流 6、事件委托的实现方法 1、vue写法 1.1、html代码 1.2、js代码 2、原生的写法其实也差不多: 2.1、…...

C++学习笔记——对象的指针
目录 一、对象的指针 二、减少对象的复制开销 三、应用案例 游戏引擎 图像处理库 数据库管理系统 航空航天软件 金融交易系统 四、代码的案例应用 一、对象的指针 是一种常用的技术,用于处理对象的动态分配和管理。使用对象的指针可以实现以下几个方面的功…...
QT5.14 实现ModbusTCP客户端 Demo
本文在QT5.14平台,基于QModbusClientTcp类,实现了客户端对单个寄存器的读写,用ModbusSlave做服务器做测试。 1.界面 (1)更改读按钮的名称为bt_Read (2)更改写按钮的名称为bt_Write 2.修改pro文件的第三行 greaterThan(QT_MAJOR_VERSION, 4)…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
