统计学-R语言-3
文章目录
- 前言
- 给直方图增加正态曲线的不恰当之处
- 直方图与条形图的区别
- 核密度图
- 时间序列图
- 洛伦茨曲线
- 计算绘制洛伦茨曲线所需的各百分比数值
- 绘制洛伦茨曲线
- 练习
前言
本篇文章是介绍对数据的部分图形可视化的图型展现。
给直方图增加正态曲线的不恰当之处
需要注意的是,给直方图拟合正态分布曲线并非总是适用,有时甚至是荒谬的,容易产生误导。合理的做法是为直方图拟合一条核密度估计曲线,它是数据实际分布的一种近似描述。
下面通过一个实际例子说明给直方图拟合正态分布曲线的荒谬之处:
根据美国黄石国家公园(Yellowstone National Park)老忠实间歇喷泉(Old Faithful Geyser)数据绘制的直方图,并在直方图中分别增加了核密度估计曲线和正态分布曲线。
par(mai=c(.8,.8,.1,.1),cex=.8)
hist(faithful$eruptions, probability=TRUE, xlab="喷发持续时间",breaks=20, col="light blue",main="")
rug(faithful$eruptions)
lines(density(faithful$eruptions, bw=.1), type='l', lwd=2, col='red')
points(quantile(faithful$eruptions),c(0,0,0,0,0),lwd=5,col="red2")
points(mean(faithful$eruptions),c(0),lwd=8,col=4)
curve(dnorm(x,mean=mean(faithful$eruptions),sd=sd(faithful$eruptions)),add=T,col="blue",lwd=2,lty=6)
图显示有两个明显的峰值,用核密度估计曲线可清晰地看出喷发持续时间属于双峰分布,可见为该直方图拟合正态分布曲线的荒之处。
直方图与条形图的区别
条形图中的每一矩形表示一个类别,其宽度没有意义;
直方图的宽度则表示各组的组距分组数据具有连续性,直方图的各矩形通常是连续排列;
而条形图则是分开排列条形图主要用于展示类别数据,而直方图则主要用于展示数值数据。
核密度图
核密度估计(density estimation)是根据一定的核(kernel)函数和适当的带宽(band-width)对数据的分布密度做出的估计。
核密度图(kernel density plot)是对核密度估计的一种描述,利用该图可看出数据的实际分布状况.以例2-3的数据为例,绘制6名运动员射击成绩核密度估计曲线。
R代码和结果如下所示:
# 用lattice包绘制核密度曲线
load("C:/example/ch2/example2_3_1.RData")
library(lattice)
dp1<-densityplot(~射击环数|运动员,data=example2_3_1,col="blue",cex=0.4,par.strip.text=list(cex=0.6),sub="(a)栅格图")# 用lattice包绘制例2-3的核密度比较曲线
dp2<-densityplot(~射击环数,group=运动员,data=example2_3_1,auto.key=list(columns=1,x=0.01,y=0.95,cex=0.6),cex=0.4,sub="(b)比较图")
# 组合latiice包的绘图
plot(dp1,split=c(1,1,2,1))
plot(dp2,split=c(2,1,2,1),newpage=F)
该图显示了每名运动员射击成绩分布的核密度估计曲线(图中的“ o”为扰动点)。
load("C:/example/ch2/example2_3_1.RData")
attach(example2_3_1)
library(sm)
par(cex=0.8,mai=c(.7,.7,.1,.1))
sm.density.compare(射击环数,运动员,lty=1:6,col=c("black","blue","brown","darkgreen","green","red"),lwd=2)
legend("topleft",legend=levels(运动员),lty=1:6,,col=c("black","blue","brown","darkgreen","green","red"))
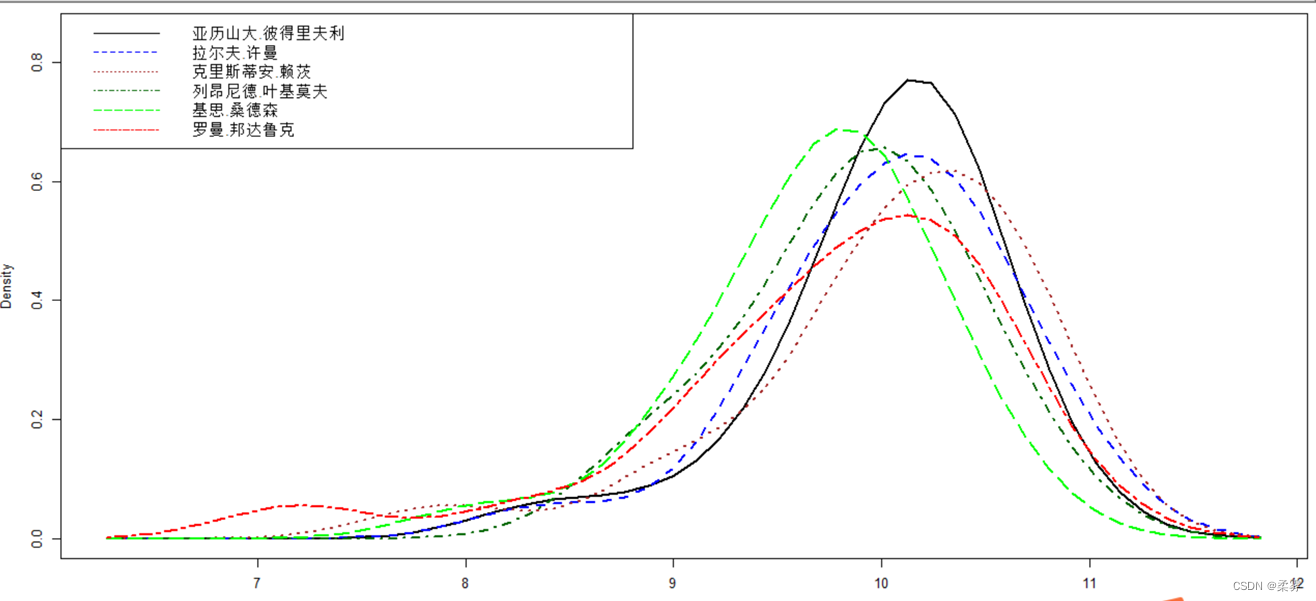
该图显示了6名运动员射击成绩分布的核密度估计比较曲线容易看出,6名运动员射击成绩均呈现左偏分布。这是因为射击环数的中心点是10.99.环数的上界已被限定,而下界(0环)则远离中心点.因此,下界值方向出现远离中心点的环数的可能性大于上界值方向。此外,从6名运动员射击成绩的分布看,除了基思桑德森,其他运动员射击成绩的分布中心均很接近最高环数(10.99)。
时间序列图
load("C:/example/ch2/example2_9.RData")
example2_9<-ts(example2_9,start=2000)
par(mai=c(0.7,0.7,0.1,0.1),cex=0.8,fg=2)
plot(example2_9[,2],lwd=2,ylim=c(2000,30000),xlab="年份",ylab="居民消费水平",type="n")
grid(col="gray60")
points(example2_9[,2],type='o',lwd=2,ylim=c(2000,30000),xlab="年份",ylab="居民消费水平")
lines(example2_9[,3],type='b',lty=2,lwd=2,col="blue")
legend(x="topleft",legend=c("农村居民消费水平","城镇居民消费水平"),lty=1:2,col=c(1,4),cex=0.8)
函数ts(data, start,…)用于创建时间序列对象,参数data为向量、矩阵或数据框; start设定时间序列的起始时间。
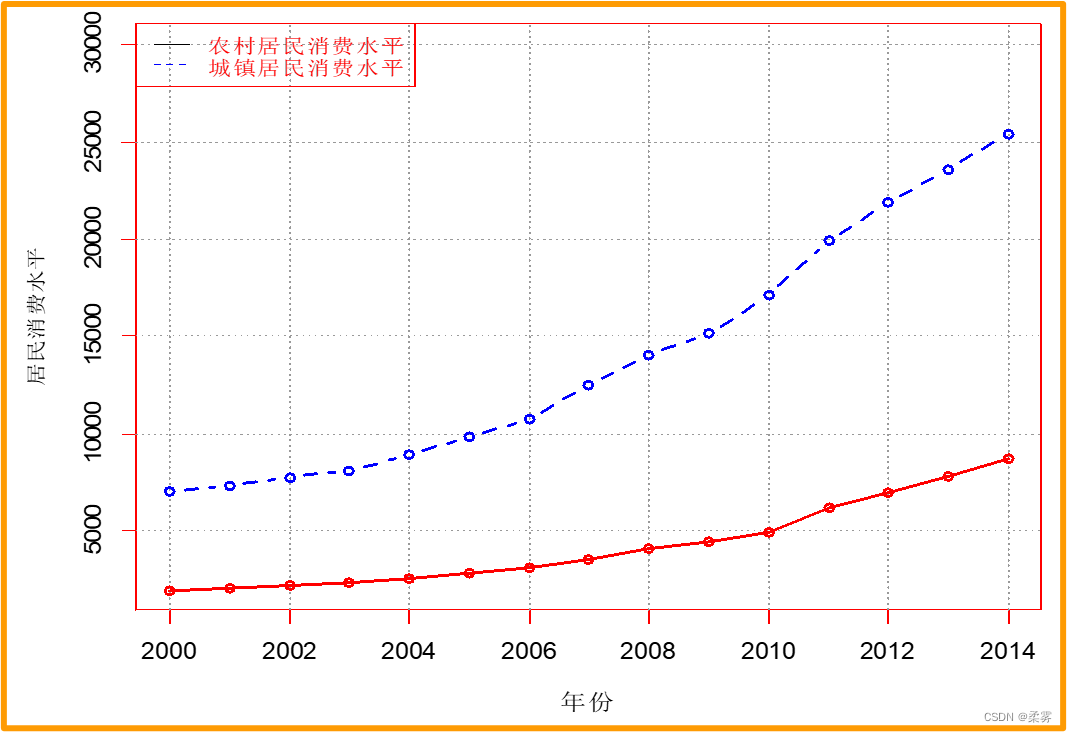
图显示,无论是农村居民还是城镇居民,消费水平随时间的推移均呈现逐年提高的趋势,但城镇居民的消费水平各年均高于农村居民,而且随时间的推移消费水平的差距有扩大的趋势。
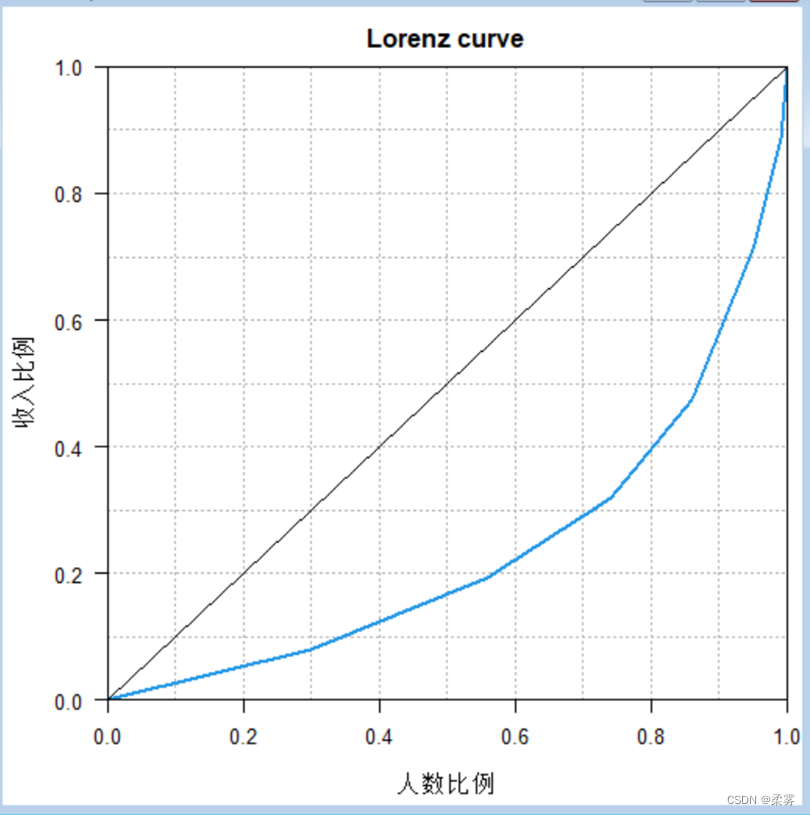
洛伦茨曲线
在频数分布中,如果将各类别的频数逐级累加,即可得到累积频数分布表。根据累加频数分布表可以绘制累加频数分布曲线。
洛伦茨曲线(Lorenz curve)是一种特殊的累积频数分布曲线,它是20世纪初由美国统计学家洛伦茨(M. E. Lorentz)根据意大利经济学家帕累托(V. Pareto)提出的收入分配公式绘制的描述收入和财富分配不平等程度的曲线。
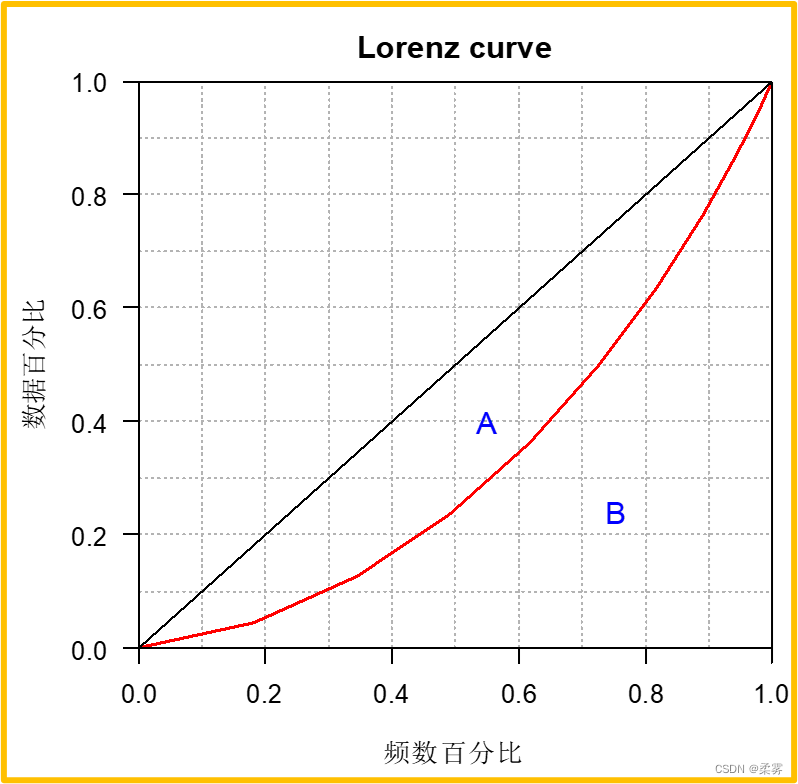
图中弯曲的线就是洛伦茨曲线
如果用横轴表示人口百分比,纵轴表示相应人口获得的收入百分比,通过洛伦兹曲线,可以直观地反映一个国家或地区收入分配平等或不平等的状况
如果一定累积百分比的人口获得相同累积百分比的收入,就是图中的对角线,即收入分配绝对平均线。
如果绝大多数人口占有很少的收入,而一小部分人口占有绝大部分的收入,则洛伦茨曲线就靠近下横轴和右纵轴形成弯曲的线。弯曲程度越大,表示收入分配越不公平。
为更准确的反映收入分配的不平等程度,20世纪初意大利经济学家基尼(C. Gini)根据洛伦茨曲线给出了衡量收入分配平等程度的指标,即基尼系数(Gini coefficient),用公式表示为:

计算绘制洛伦茨曲线所需的各百分比数值
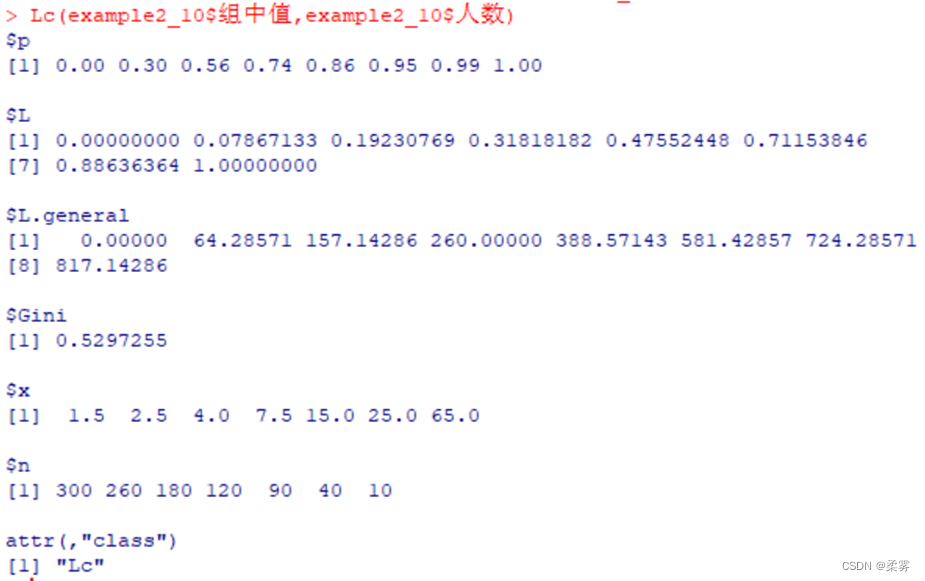
load("C:/example/ch2/example2_10.RData")
library(DescTools)
Lc(example2_10$组中值,example2_10$人数)
绘制洛伦茨曲线
par(mai=c(0.7,0.7,0.4,0.1),cex=0.8)
plot(Lc(example2_10$组中值,example2_10$人数),xlab="人数比例",ylab="收入比例",col=4,panel.first=grid(10,10,col="gray70"))

练习
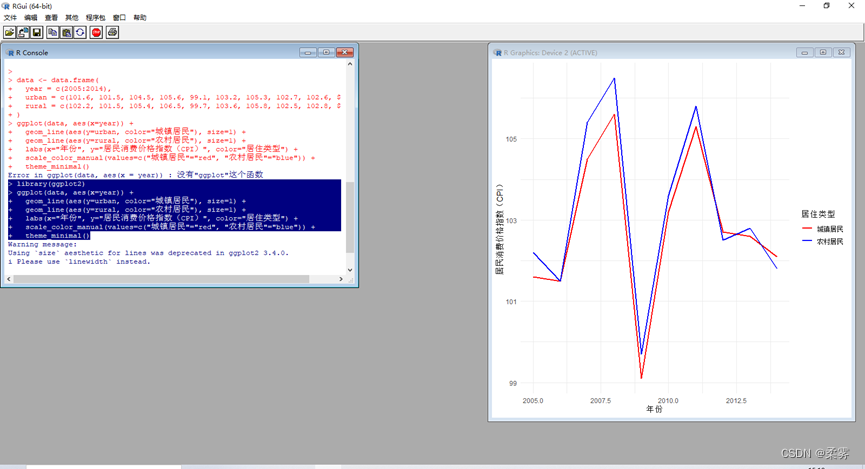
1、(数据: exercise2_5.RData)exercise2_5.RData数据是2005—2014年我国城镇居民和农村居民的居民消费价格指数(CPI)数据。
绘制时间序列图,观察城镇居民和农村居民消费价格指数的变化特征。
library(ggplot2)
ggplot(data, aes(x=year)) geom_line(aes(y=urban, color="城镇居民"), size=1) geom_line(aes(y=rural, color="农村居民"), size=1) + abs(x="年份", y="居民消费价格指数(CPI)", color="居住类型") scale_color_manual(values=c("城镇居民"="red", "农村居民"="blue")) theme_minimal()
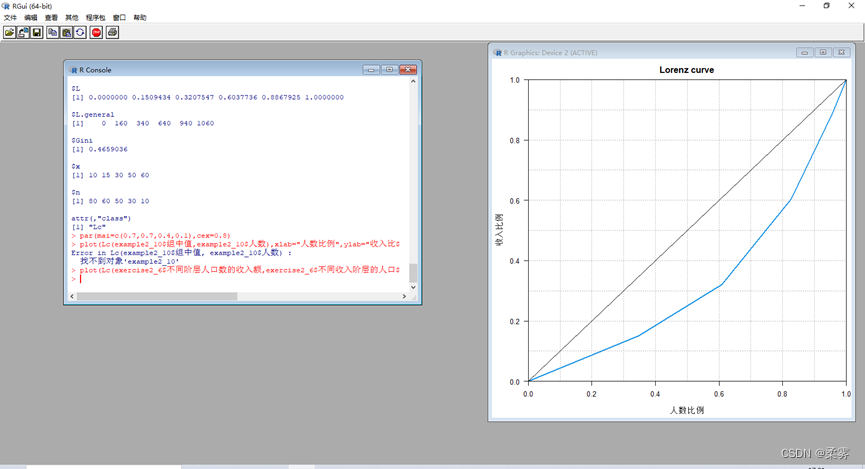
2、(数据: exercise2_6.RData)假定某地区不同收入阶层的人口数和不同阶层人口的年收入额如数据 exercise2_6.RData所示。
绘制洛伦兹曲线分析收入分配的不平等程度。
load("C:/ch2/ch2/exercise/exercise2_6.RData")
library(DescTools)
Lc(exercise2_6$不同阶层人口数的收入额,exercise2_6$不同收入阶层的人口数)
par(mai=c(0.7,0.7,0.4,0.1),cex=0.8)
plot(Lc(exercise2_6$不同阶层人口数的收入额,exercise2_6$不同收入阶层的人口数),xlab="人数比例",ylab="收入比例",col=4,panel.first=grid(10,10,col="gray70"))
相关文章:

统计学-R语言-3
文章目录 前言给直方图增加正态曲线的不恰当之处直方图与条形图的区别核密度图时间序列图洛伦茨曲线计算绘制洛伦茨曲线所需的各百分比数值绘制洛伦茨曲线 练习 前言 本篇文章是介绍对数据的部分图形可视化的图型展现。 给直方图增加正态曲线的不恰当之处 需要注意的是&#…...

spring动态控制定时任务
在spring框架中,对于简单的定时任务,可以使用 Scheduled 注解实现,在实际项目中,经常需要动态的控制定时任务,比如通过接口增加、启动、停止、删除定时任务,动态的改变定时任务的执行时间等。 我们可以通过…...

3. Mybatis 中SQL 执行原理
2. Mybatis 中SQL 执行原理 这里有两种方式,一种为常用的 Spring 依赖注入 Mapper 的方式。另一种为直接使用 SqlSessionTemplate 执行 Sql 的方式。 Spring 依赖注入 Mapper 的方式 Mapper 接口注入 SpringIOC 容器 Spring 容器在扫描 BeanDefinition 阶段会扫…...
第一次在RUST官方论坛上留言发布我的Rust板箱
第一次在RUST官方论坛上发帖子,有点紧张~地址在这里: 【My Rust Crate】obtains linux local information - The Rust Programming Language Forum (rust-lang.org)...

LabVIEW 智能化矿用定向钻机液压系统监测
简介 在矿用定向钻机的液压系统监测中,实现实时监控和异常预警对于保障设备运行的稳定性至关重要。传统的人工监测方法效率低下而且准确性不能满足要求,针对这种情况采用 LabVIEW 开发平台,设计并实现了一套智能化矿用定向钻机液压系统的状态…...

GO数据库操作
Golang 出色的 ORM 库为 GORM。 官网文档:https://gorm.io/docs/ 我们来说说增删改查的用法,更深入的研究可以去官网看看。 GORM功能概览: 关联(有一个、有多个、属于、多对多、多态性、单表继承)挂钩(创…...

PyTorch简单理解ChannelShuffle与数据并行技术解析
目录 torch.nn子模块详解 nn.ChannelShuffle 用法与用途 使用技巧 注意事项 参数 示例代码 nn.DataParallel 用法与用途 使用技巧 注意事项 参数 示例 nn.parallel.DistributedDataParallel 用法与用途 使用技巧 注意事项 参数 示例 总结 torch.nn子模块详…...
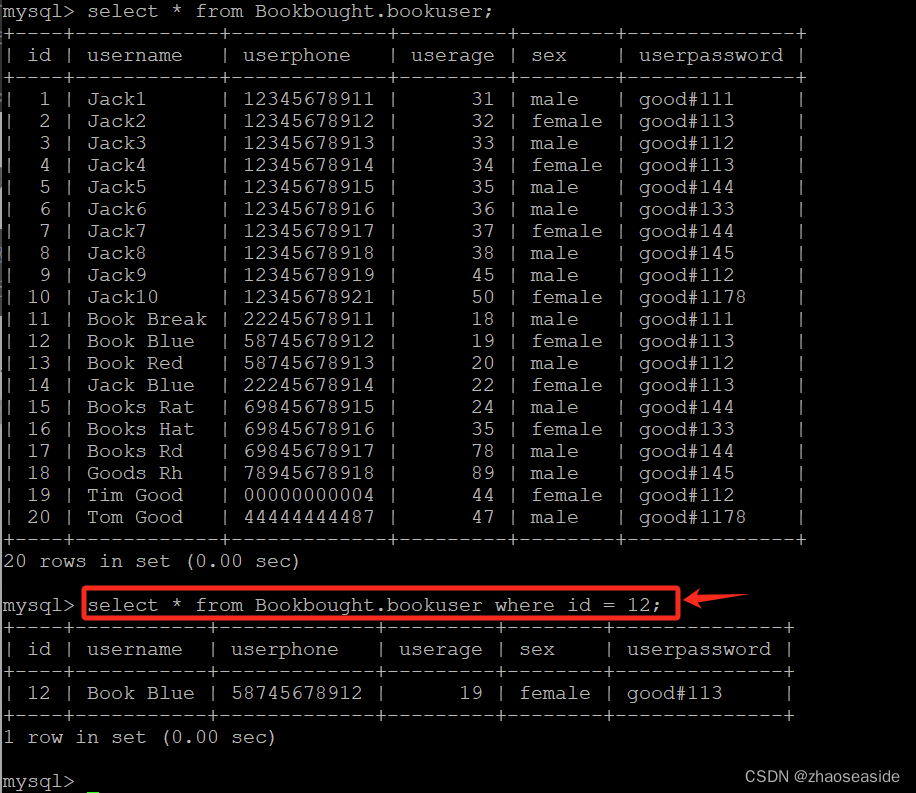
MySQL 8查询语句之查询所有字段、特定字段、去除重复字段、Where判断条件
《MySQL 8创建数据库、数据表、插入数据并且查询数据》里边有我使用到的数据。 再使用下方的语句补充一些数据: insert into Bookbought.bookuser(id,username,userphone,userage,sex,userpassword) values (11,Book Break,22245678911,18,male,good#111); insert…...

LLaMA-Factory添加adalora
感谢https://github.com/tsingcoo/LLaMA-Efficient-Tuning/commit/f3a532f56b4aa7d4200f24d93fade4b2c9042736和https://github.com/huggingface/peft/issues/432的帮助。 在LLaMA-Factory中添加adalora 1. 修改src/llmtuner/hparams/finetuning_args.py代码 在FinetuningArg…...
多端多用户万能DIY商城系统源码:自营+多商户入驻商城系统 独立部署 带完整的安装代码包以及搭建教程
电子商务行业日新月异,许多企业希望能够通过线上商城拓展业务。但是,传统商城系统往往无法满足多样化、个性化的需求,而且开发周期长、成本高。罗峰就来给大家分享一款多端多用户万能DIY商城系统源码,搭建简单。 以下是部分代码示…...

Qt 6之七:学习资源
Qt 6之七:学习资源 Qt是一种跨平台的C应用程序开发框架,它提供了一套丰富的工具和库,可以帮助开发者快速构建跨平台的应用程序,用于开发图形用户界面(GUI)和非GUI应用程序。 Qt 6之一:简介、安…...

解决大模型的幻觉问题:一种全新的视角
在人工智能领域,大模型已经成为了一个重要的研究方向。然而,随着模型规模的不断扩大,一种新的问题开始浮出水面,那就是“幻觉”问题。这种问题的出现,不仅影响了模型的性能,也对人工智能的发展带来了新的挑…...

mysql进阶-重构表
目录 1. 原因 2. 如何重构表呢? 2.1 命令1: 2.2 命令2: 2.3 命令3: 1. 原因 正常的业务开发,为什么需要重构表呢? 原因1:某张表存在大量的新增和删除操作,导致表经历过大量的…...

Element-ui图片懒加载
核心代码 <el-image src"https://img-blog.csdnimg.cn/direct/2236deb5c315474884599d90a85d761d.png" alt"我是图片" lazy><img slot"error" src"https://img-blog.csdnimg.cn/direct/81bf096a0dff4e5fa58e5f43fd44dcc6.png&quo…...

Linux系统——DNS解析详解
目录 一、DNS域名解析 1.DNS的作用 2.域名的组成 2.1域名层级结构关系特点 2.2域名空间构成 2.3域名的四种不同类型 2.3.1延伸 2.3.2总结 3.DNS域名解析过程 3.1递归查询 3.2迭代查询 3.3一次DNS解析的过程 4.DNS系统类型 4.1缓存域名服务器 4.2主域名服务器 4…...
初识Ubuntu
其实还是linux操作系统 命令都一样 但是在学习初级阶段,我还是将其分开有便于我的学习和稳固。 cat 查看文件 命令 Ubuntu工作中经常是用普通用户,在需要时才进行登录管理员用户 sudn -i 切换成管理用户 我们远程连接时 如果出现 hostname -I没有出现…...

Casper Network (CSPR)2024 年愿景:通过投资促进增长
Casper Network (CSPR)是行业领先的 Layer-1 区块链网络之一,通过推出了一系列值得关注的技术改进和倡议,已经为 2024 年做好了准备。 在过去的一年里,Casper Network (CSPR)不断取得里程碑式的进展,例如推…...

《MySQL系列-InnoDB引擎06》MySQL锁介绍
文章目录 第六章 锁1 什么是锁2 lock与latch3 InnoDB存储引擎中的锁3.1 锁的类型3.2 一致性非锁定读3.3 一致性锁定读3.4 自增长与锁3.5 外键和锁 4 锁的算法4.1 行锁的三种算法4.2 解决Phantom Problem 5 锁问题5.1 脏读5.2 不可重复读5.3 丢失更新 6 阻塞7 死锁 第六章 锁 开…...

获取多个PDF文件的内容并保存到excel上
# shuang # 开发时间:2023/12/9 22:03import pdfplumber import re import os import pandas as pd import datetimedef re_text(bt, text):# re 搜索正则匹配 包含re.compile包含的文字内容m1 re.search(bt, text)if m1 is not None:return re_block(m1[0])return…...

深入了解网络流量清洗--使用免费的雷池社区版进行防护
随着网络攻击日益复杂,企业面临的网络安全挑战也在不断增加。在这个背景下,网络流量清洗成为了确保企业网络安全的关键技术。本文将探讨雷池社区版如何通过网络流量清洗技术,帮助企业有效应对网络威胁。 ![] 网络流量清洗的重要性&#x…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
