什么是数通技术?以太网交换机在数通技术中的精要
什么是数通技术?
数通技术是指数字通信技术,它涵盖了数字信号处理、数据传输、网络通信等领域。通信工程师在数通技术中负责设计、建设和维护数字通信系统,以实现可靠、高效的信息传输。这涉及到数字信号的编解码、调制解调、数据压缩、网络协议等方面的技术。数通技术在现代社会中广泛应用,包括互联网、移动通信、卫星通信等领域。
数通技术可以被看作是传统通信技术的升级和演进。传统通信技术主要涉及模拟信号的传输,而数通技术引入了数字信号的概念,通过数字化处理信息,提供了更高效、可靠、灵活的通信方式。
传统通信技术的特点包括模拟信号的传输和处理,而这在一定程度上受到了信号衰减、噪声干扰等因素的影响。随着数通技术的兴起,数字信号的使用使得通信系统更容易处理、存储和传输信息,提高了抗干扰能力,并拓展了通信系统的功能和应用范围。
数通技术有哪些原理
数通技术涉及多个领域,以下是一些主要原理和概念:
数字信号处理(DSP): 数字信号处理是将模拟信号转换为数字形式,进行数字化处理的过程。这包括采样、量化和编码。数字信号的优势在于可以更容易地进行处理、存储和传输。
调制和解调: 调制是将数字信号转换为模拟信号,而解调则是将模拟信号还原为数字信号。调制技术有多种类型,如调幅调制(AM)、调频调制(FM)和调相调制(PM),它们用于在信号传输中携带信息。
数据压缩: 为了有效利用带宽和存储资源,数字通信系统通常使用数据压缩技术。这包括有损压缩和无损压缩,前者在一定程度上丢失信息以减小文件大小,而后者保持所有信息但可能效率较低。
网络协议: 在网络通信中,使用各种协议来确保数据的正确传输。TCP/IP协议是互联网上最常见的协议之一,它负责数据包的分组、传输和重新组装。
数字通信系统: 数通技术涉及构建数字通信系统,这包括发送和接收数据的设备、信道编码、差错检测和纠正、调制解调器等组件。系统的设计要考虑信道特性、带宽、误码率等因素。
光纤通信: 在光纤通信中,光信号被用于传输信息。这涉及激光器的发射、光纤的传输和光探测器的接收。光纤通信具有高带宽和低信号衰减的优势。
移动通信: 移动通信系统使用蜂窝结构,通过基站和移动设备进行通信。这涉及频分多址(FDMA)、时分多址(TDMA)、码分多址(CDMA)等多种技术来实现多用户同时通信。
以上是数通技术的一些基本原理,实际应用中可能涉及更多的细节和先进技术。这些原理共同确保数字通信系统的稳定、高效运作。

数通技术中的以太网交换机
以太网交换机在数通技术中扮演着关键的角色,主要涉及到局域网(LAN)中的数据交换和网络连接。以下是以太网交换机的一些主要功能和角色:
数据帧转发: 以太网交换机通过学习每个连接到它的设备的MAC地址,建立一个地址表。当接收到数据帧时,交换机会查看目标MAC地址,并将数据帧只转发到相应的端口,而不是广播到所有端口。这样可以提高网络效率。
广播和碰撞域隔离: 以太网交换机可以隔离局域网中的广播域和碰撞域。广播仅限于发送广播的端口,而不是整个网络,从而减少了网络上的广播流量。此外,由于每个端口形成一个独立的冲突域,碰撞几乎不会发生。
虚拟局域网(VLAN)支持: 以太网交换机支持VLAN技术,允许将网络划分为多个虚拟网络。这有助于提高网络的安全性和管理灵活性,因为不同的VLAN可以隔离不同的用户群体。
流量控制和速率匹配: 交换机能够管理流量,确保网络中的设备不会因为过多的数据导致拥塞。此外,交换机能够进行速率匹配,使得连接到不同速度的设备之间的通信更加有效。
链路聚合: 以太网交换机支持链路聚合技术,允许将多个物理链路组合成一个逻辑链路,以提高带宽和提供冗余。
质量服务(QoS): 交换机可以基于服务质量标签对不同类型的数据流进行优先处理,确保对实时应用(如VoIP)的低延迟和高优先级。
总体而言,以太网交换机通过智能地管理数据流,提高了局域网的性能、安全性和灵活性,是现代数通技术中不可或缺的组件之一。
相关文章:

什么是数通技术?以太网交换机在数通技术中的精要
什么是数通技术? 数通技术是指数字通信技术,它涵盖了数字信号处理、数据传输、网络通信等领域。通信工程师在数通技术中负责设计、建设和维护数字通信系统,以实现可靠、高效的信息传输。这涉及到数字信号的编解码、调制解调、数据压缩、网络…...

php 的数学常用函数
目录 1.常用列表 2.代码示例 1.常用列表 函数名描述输入输出abs()求绝对值数字绝对值数字ceil()进一法取整浮点数进一取整floor()舍去法求整浮点数直接舍去小数部分fmod()浮点数取余 两个浮点 数,x>y 浮点余数 pow()返回数的n次方基础数n次方乘方值round()浮点数四舍五入…...

Netty-Netty组件了解
EventLoop 和 EventLoopGroup 回想一下我们在 NIO 中是如何处理我们关心的事件的?在一个 while 循环中 select 出事 件,然后依次处理每种事件。我们可以把它称为事件循环,这就是 EventLoop 。 interface io.netty.channel. EventLoo…...

银行的压力测试如何进行?
为什么要进行压力风险测试? 压力风险测试的最终目的是测试银行在极度恶劣的市场环境中是否有足够的资本维持运转。 题主链接中的一级资本充足率(Tier 1 capital ratio) 亦即衡量标准,这个数字越大,表明银行资本约充裕,可以在停止…...

QtService、托盘程序使用
1、QtService 使用QtService实现Qt后台服务程序 用QT创建一个Windows Service以及踩到的若干坑 2、托盘程序 Qt之程序最小化托盘显示及操作 Qt系统托盘程序的实现...

使用Linux防火墙管理HTTP流量
在Linux系统中,防火墙是用于控制网络流量的重要工具。通过防火墙,你可以根据需要限制、过滤或允许特定的网络流量,从而提高系统的安全性。在处理HTTP流量时,防火墙可以帮助你实施访问控制、流量监控和其他安全策略。 iptables i…...
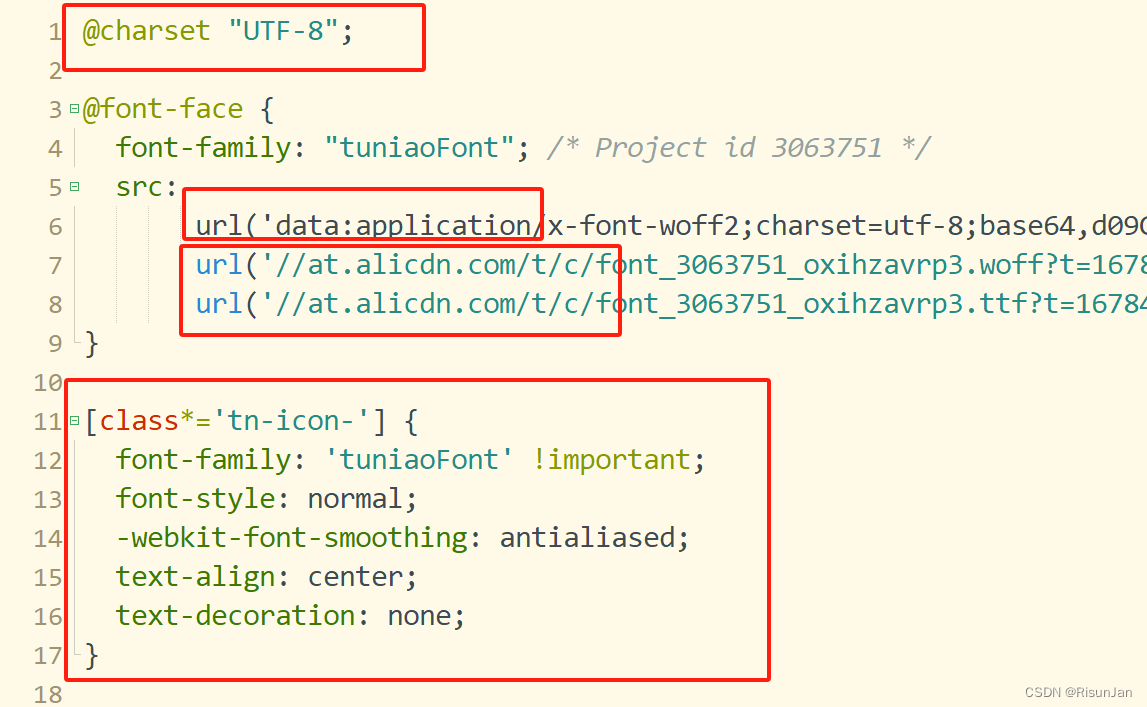
图鸟引入多套字体图标的方式教程
https://www.yuque.com/tuniao/qunyou/tgfvpg ①上传icon,生成iconfont.css 将css文件放这里 app.vue全局引入 适当改造iconfont.css的写法,方便调用...

在openEuler环境下快速编译GreatSQL RPM包
在上一篇中,已经介绍了在CentOS环境下编译GreatSQL RPM包的过程,本文再介绍如何在openEuler环境下编译GreatSQL RPM包。 运行环境是docker中的openEuler 22.03 x86_64: $ docker -v Docker version 20.10.10, build b485636$ docker run -itd…...
C语言基础语法跟练 day3
31、不使用累计乘法的基础上,通过移位运算(<<)实现2的n次方的计算。 #include <stdio.h> int main() {int i 0;scanf("%d",&i);printf("%d",1<<i);return 0; } 32、问题:一年约有 3.…...

【控制篇 / 策略】(7.4) ❀ 01. IP地理位置数据库和地理地址对象 ❀ FortiGate 防火墙
【简介】在很多使用环境下,我们需要对指定国家的IP地址进行允许或禁止访问操作,例如只允许访问国内IP。以前只能手动添加IP地址对象到地址组,繁杂且效率低下,Fortinet提供了基于地理位置的IP库,就可以解决这个问题。 I…...
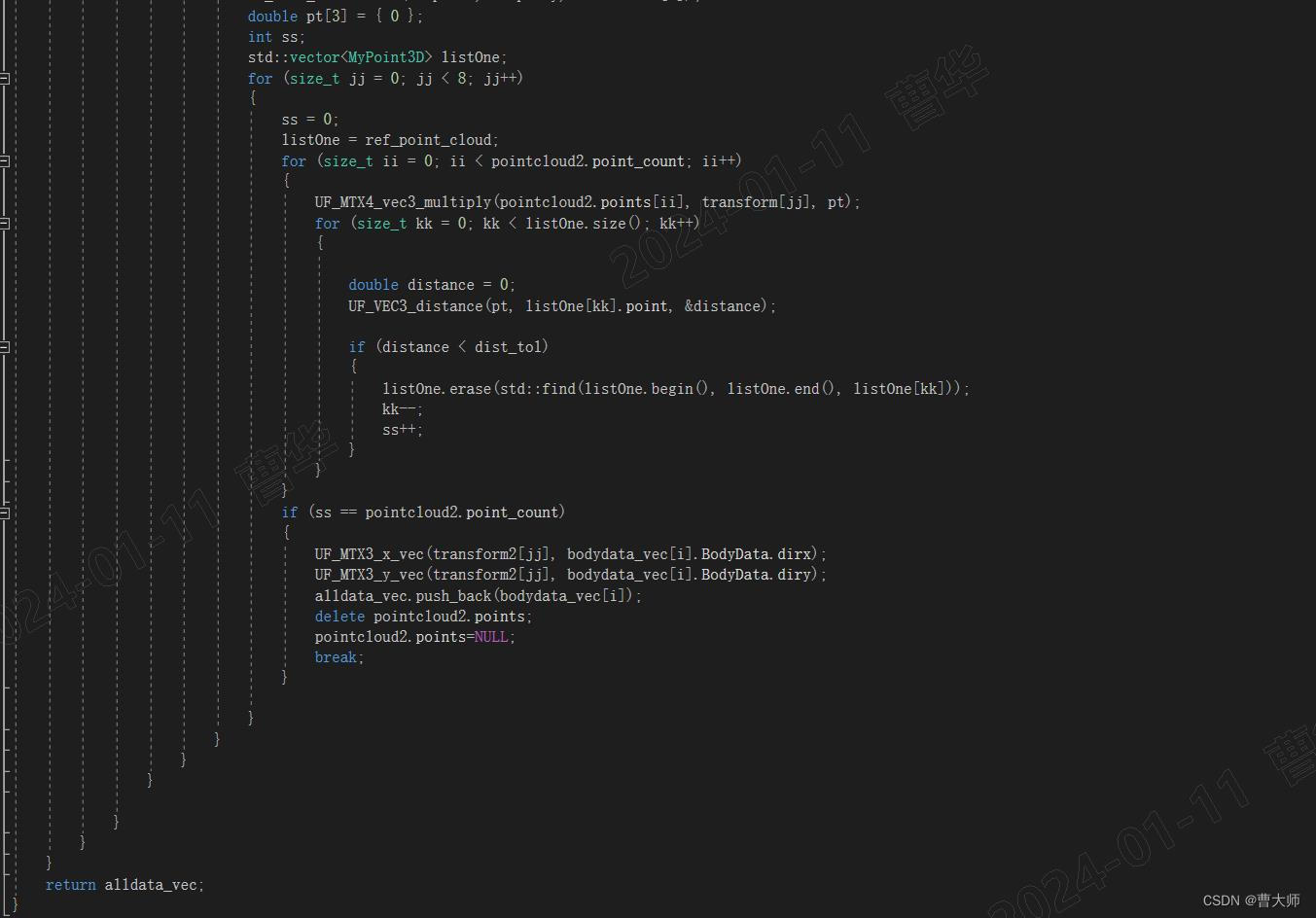
NX二次开发点通过云配准获取相同体
先找到体的参考方向(这个参考方向对于相同体重合之后是相同的),这个时候我们的思路是三个不共线的点确定一个坐标系,然后和绝对方向求转换矩阵。然后获取体的所有边的几何中心,把这些点通过转换矩阵转换之后存起来&…...
)
5.4 Android BCC环境搭建(eadb版 下)
四,BCC使用示例 这里以tcplife为例,来显示TCP会话的生命周期和吞吐量统计。 4.1 进入/bcc/tools目录 root@localhost:/bcc# cd tools/ root@localhost:/bcc/tools# ls CMakeLists.txt javacalls.sh rubystat_example.txt argdist.py javacalls_e…...

【AI视野·今日Robot 机器人论文速览 第七十四期】Wed, 10 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Wed, 10 Jan 2024 Totally 17 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Hold em and Fold em: Towards Human-scale, Feedback-Controlled Soft Origami Robots Authors Immanuel Ampomah Mensah, Je…...
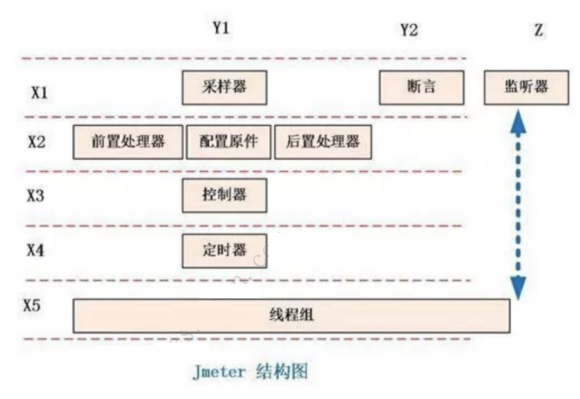
服务端性能测试——性能测试工具JMeter-L1
第一遍没学懂,后续文章会更新~ 目录: 1.JMeter介绍与安装Meter简介JMeter安装2.JMeter的运行JMeter运行、界面功能简介3.使用代理服务器录制请求录制压测脚本(一)Web端脚本录制方法4.测试计划5.线程组6.控制器7.JMeter采样器/取…...
C# OpenCvSharp DNN FreeYOLO 目标检测
目录 效果 模型信息 项目 代码 下载 C# OpenCvSharp DNN FreeYOLO 目标检测 效果 模型信息 Inputs ------------------------- name:input tensor:Float[1, 3, 192, 320] --------------------------------------------------------------- Outp…...
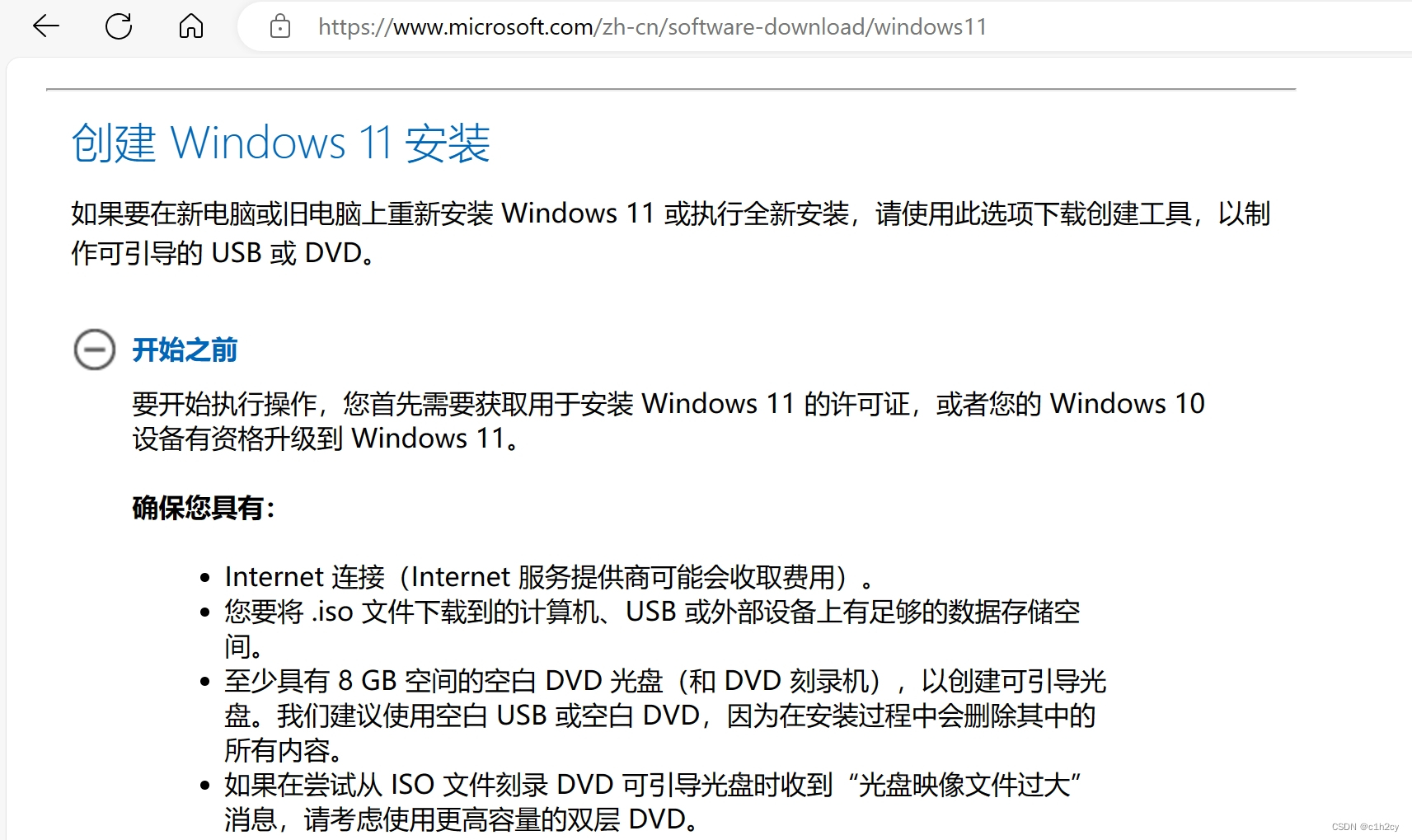
U盘启动安装win11遇到缺少计算机所需的介质驱动程序问题
一、使用U盘制作启动盘遇到问题 下载了windows原版镜像,验证了md5,确保文件没有损坏。使用ultroiso制作u盘启动盘,开始安装后出现下图的报错: 在网上搜索解决方案,主要有以下几种: 安装的时候,…...
正则表达式、文件访问(Python实现)
一、主要目的: 1.了解正则表达式的基本概念和处理过程。 2.掌握使用正则表达式模块 Re 进行字符串处理的方法。 3.了解文件的基本概念和类型。 4.掌握在 Python 中访问文本文件的方法和步骤。 5.熟悉在 Python 中访问二进制文件的方法和步骤。 二、主要内容和结…...
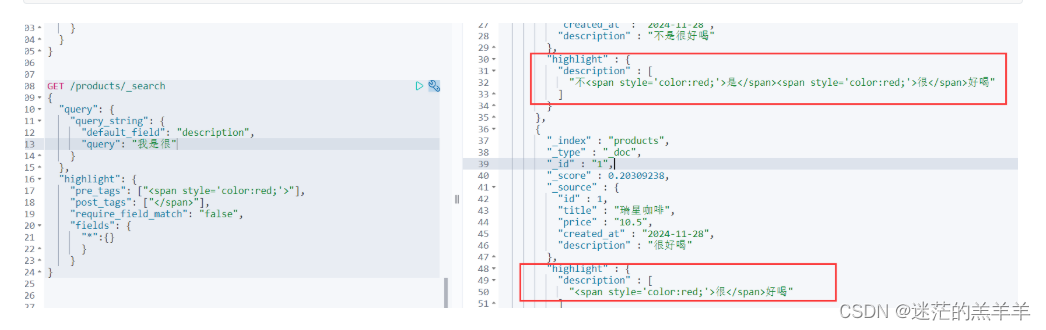
ES高级查询
ES中提供了一种强大的检索数据方式,这种检索方式称为Query DSL,这种方式的丰富查询语法让ES检索变得更强大,更简洁。 1.常见查询 1.1查询所有[match_all] match_all关键字:返回索引中的全部文档。 GET /products/_search { &…...

RT-Thread入门笔记6-空闲线程及两个常用的钩子函数
空闲线程 空闲线程是一个比较特殊的系统线程,它具备最低的优先级。当系统中无其他就绪线程可运行时,调度器将调度到空闲线程。 空闲线程还负责一些系统资源回收以及将一些处于关闭态的线程从线程调度列表中移除的动作 空闲线程在形式上是一个无线循环结…...

网络正常运行时间监控工具
正常运行时间是衡量系统可靠性的指标,表示为机器工作和可用时间的百分比。当提到 IT 网络时,正常运行时间是衡量网络设备、网站和其他服务的可用性的指标。网络正常运行时间通常以百分位数来衡量,例如“五个 9”,这意味着系统在 9…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

