数据结构 模拟实现二叉树(孩子表示法)
目录
一、二叉树的简单概念
(1)关于树的一些概念
(2)二叉树的一些概念及性质
定义二叉树的代码:
二、二叉树的方法实现
(1)createTree
(2)preOrder
(3)inOrder
(4)postOrder
(5)size
(6)getLeafNodeCount
(7)getKLevelNodeCount
(8)getHeight
(9)find
(10)levelOrder
(11)isCompleteTree
三、最终代码
一、二叉树的简单概念
(1)关于树的一些概念

结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等节点为叶结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
根结点:一棵树中,没有双亲结点的结点;如上图:A
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由m(m>=0)棵互不相交的树组成的集合称为森林
(2)二叉树的一些概念及性质
概念:二叉树即为每个节点的度都小于等于2的树,即为二叉树。
性质:
1. 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 (i>0)个结点
2. 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 (k>=0)
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
4. 具有n个结点的完全二叉树的深度k为 上取整
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
若2i+1<n,左孩子序号:2i+1,否则无左孩子
若2i+2<n,右孩子序号:2i+2,否则无右孩子
定义二叉树的代码:
//孩子表示法
public class MyBinomialTree {static class TreeNode {char val;TreeNode left;TreeNode right;public TreeNode(char val) {this.val = val;}}
}二、二叉树的方法实现
(1)createTree
此方法是创建一个二叉树,里面是已经构造好了的二叉树,画图是如下情况:

代码如下:
//创建一个二叉树TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;E.right = H;C.left = F;C.right = G;return A;}在main方法中创建MyBinomialTree类的对象,调用此方法,就能创建出上面的二叉树,代码如下:
MyBinomialTree myBinomialTree = new MyBinomialTree();MyBinomialTree.TreeNode root = myBinomialTree.createTree();
(2)preOrder
此方法是前序遍历二叉树的方法,前序遍历即为根左右的顺序遍历二叉树,上图我们创建的二叉树,前序遍历为:A B D E H C F G
代码如下:
// 前序遍历void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}执行效果如下:

和上面写的顺序一样。
(3)inOrder
此方法是中序遍历的方法,中序遍历即为左根右的顺序遍历二叉树,继续照着上面的图,中序遍历为:D B E H A F C G
代码如下:
// 中序遍历 -》 左根右void inOrder(TreeNode root){if(root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}执行效果如下:
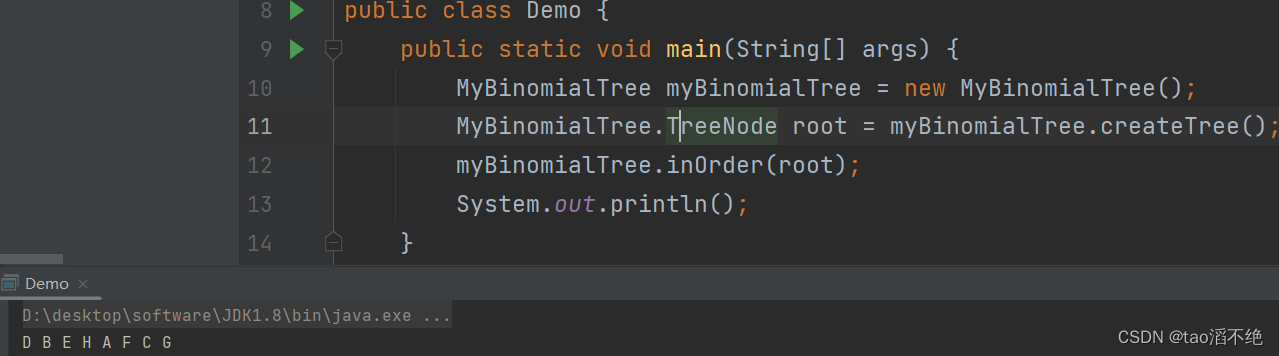
和上面写的顺序一样。
(4)postOrder
此方法是后续遍历的方法,后序遍历即为左右根的顺序遍历二叉树,照着上面创建的二叉树图,后序遍历为:D H E B F G C A
代码如下:
// 后序遍历 -》 左右根void postOrder(TreeNode root){if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}执行效果如下:

和上面写的顺序一样。
(5)size
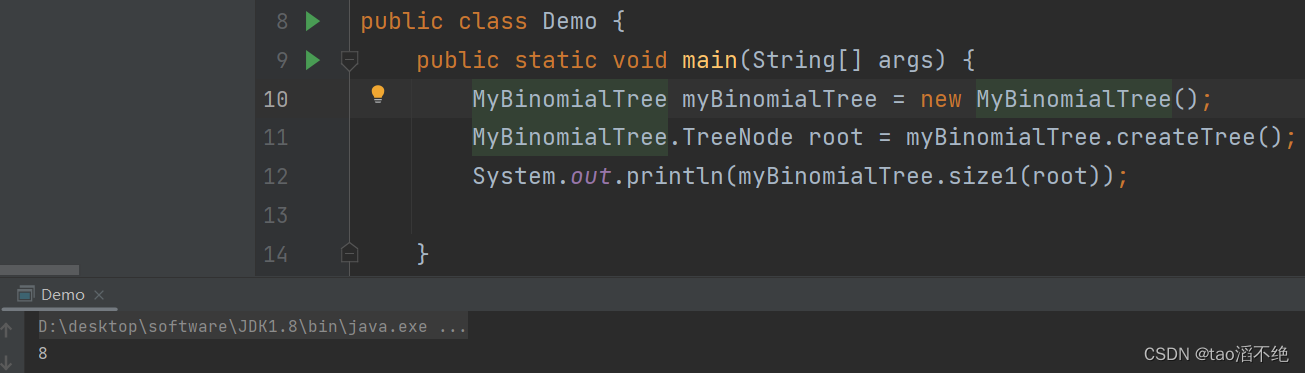
此方法是计算二叉树有多少个节点的方法,要计算二叉树有多少个节点,也意味着要遍历一遍二叉树,可以使用上面前中后序的任一遍历方法,用一个全局变量count1计数,如果遍历到当前节点不为空,则count++,最后返回count,代码如下:
public static int count1 = 0;int size1(TreeNode root) {if(root == null) {return 0;}if(root != null) {count1++;}size1(root.left);size1(root.right);return count1;}执行效果如下:
也可以使用子问题思想,二叉树的节点 = 当前root节点的左节点之和 + 当前root节点的右节点之和 + 1,如图:
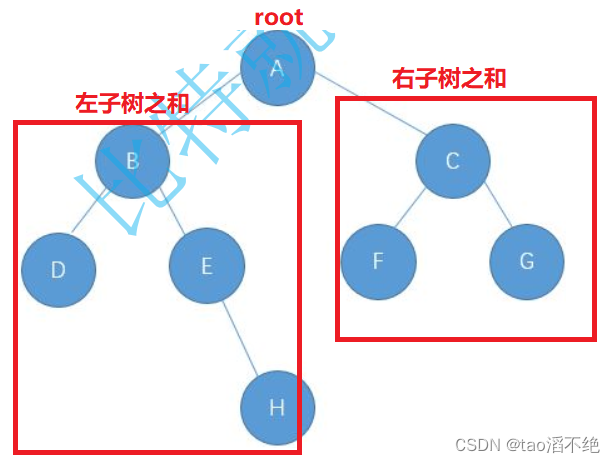 左边的子树+右边的子树+root本身自己(1)
左边的子树+右边的子树+root本身自己(1)
代码如下:
// 获取树中节点的个数int size(TreeNode root) {if(root == null) {return 0;}return size(root.left) + size(root.right) + 1;}执行效果如下:

(6)getLeafNodeCount
此方法是获取叶子节点的个数,要获取叶子节点个数,可以用遍历一遍二叉树的思想,找出二叉树那些节点即没有左孩子,也没有右孩子的节点,即叶子节点,所以要定义一个全局变量count2
代码如下:
public static int count2 = 0;// 获取叶子节点的个数int getLeafNodeCount(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {count2++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);return count2;}执行效果如下:
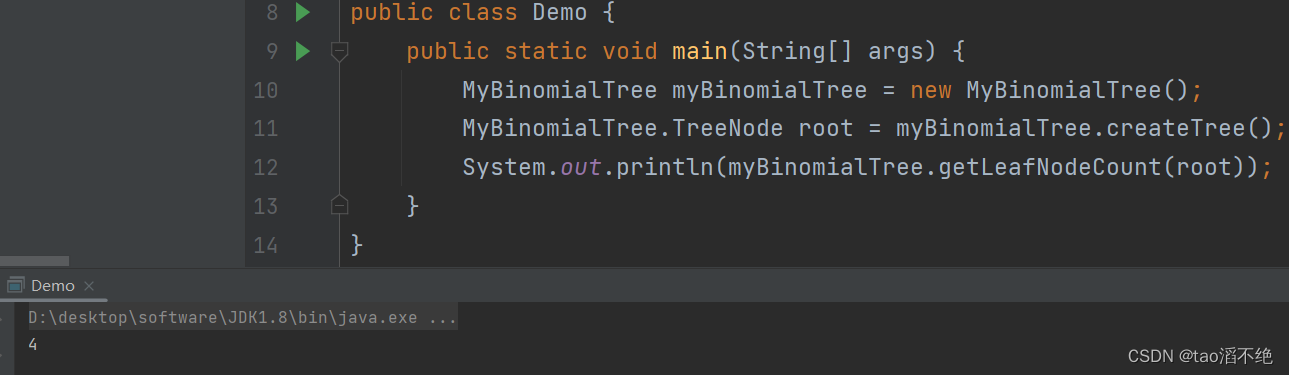
从图中可以看出,叶子节点有4个。
子问题思路:也是需要遍历二叉树,但遍历的方式不同,如果找到是叶子节点就返回1,不是则return后面加上方法的递归,即root节点的左边子树的叶子节点+右边子树的叶子节点,如图:

代码如下:
// 子问题思路-求叶子结点个数int getLeafNodeCount1(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount1(root.left) + getLeafNodeCount1(root.right);}执行效果如下: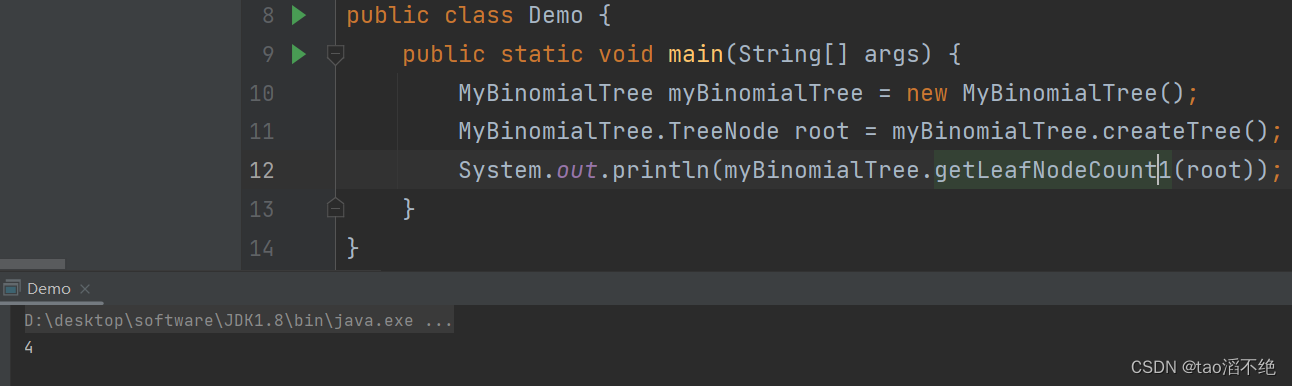
也是4个
(7)getKLevelNodeCount
此方法是获取第K层节点的个数,第K层节点的个数 = 第K-1层的所有节点的第二层节点的个数之和,如图,第三层节点的个数=第二层节点的所有节点的第一层节点的个数之和,即B节点的第一层节点之和+C节点的第一层节点之和,而第一层节点个数只能为1。

代码如下:
// 获取第K层节点的个数int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}if(k == 1) {return 1;}return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);}执行效果如下:
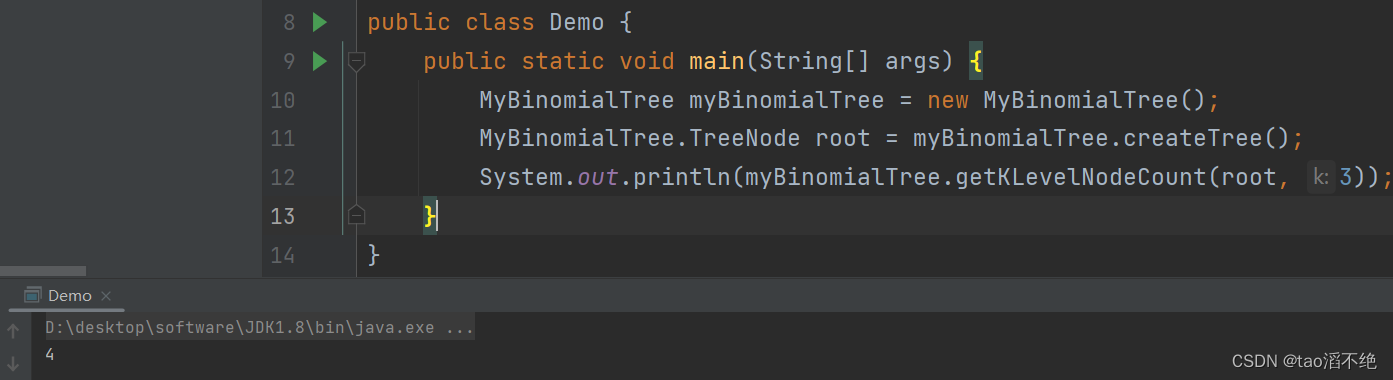
从上图可以看出第三层节点有4个,和代码运行出的结果一样。
(8)getHeight
此方法是获取二叉树的高度,要获取二叉树的高度,就需要找出root节点下面每个分支的最高高度,然后再+1,如图:

很显然,上面二叉树的高度是3+1=4
代码如下:
// 获取二叉树的高度int getHeight(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return Math.max(getHeight(root.left), getHeight(root.right)) + 1;}执行结果如下: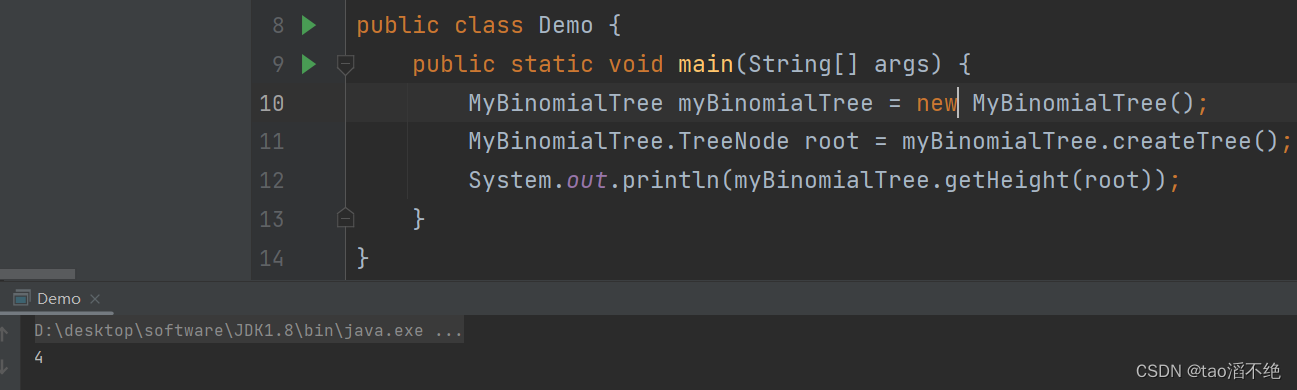
和预期结果一样。
(9)find
此方法是检测值为value的元素是否存在,要检查某个节点是否存在,就要对二叉树进行遍历,这里使用前序的遍历方法,但要注意,递归的时候要保存节点,所以要创建新的二叉树保存返回的节点
代码如下:
// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val) {if(root == null) {return null;}if(root.val == val) {return root;}TreeNode ret1 = find(root.left, val);if(ret1 != null) {return ret1;}TreeNode ret2 = find(root.right, val);if(ret2 != null) {return ret2;}return null;}执行效果如下:

上面的二叉树存在 'C' 这个节点,假如找 'X' 节点,则不会存在,会是null,如图:

(10)levelOrder
此方法是层序遍历,层序遍历是从左到右,从上到下的遍历顺序,上图的二叉树层序遍历为:
A B C D E F G H
这里需要使用到队列,用上面的二叉树为例子,下面展示二叉树的节点存放进队列的顺序,如下:
先把根节点存放进队列,如下图:
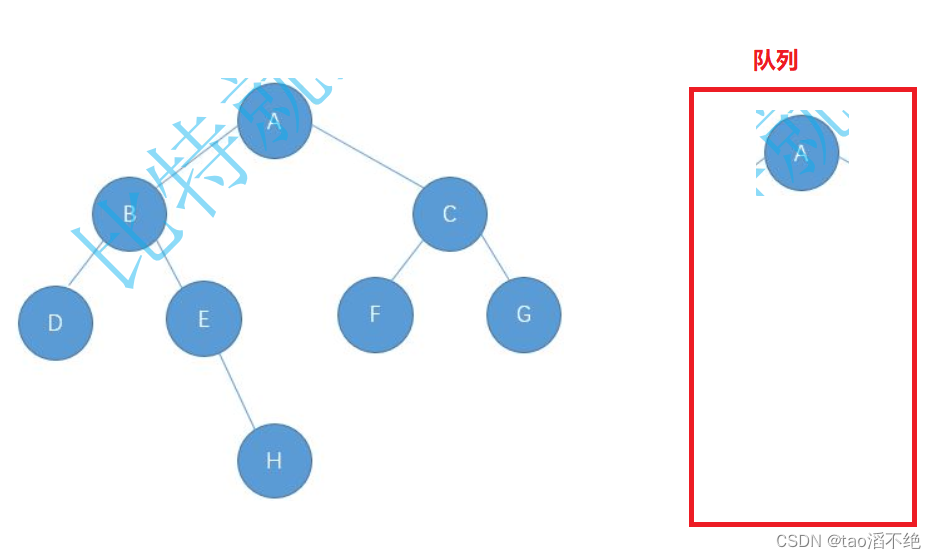
判断队列是不是空,不是空就出队列的元素,分别判断这个元素有没有左节点和右节点,如果有,就存进队列里,如下图:
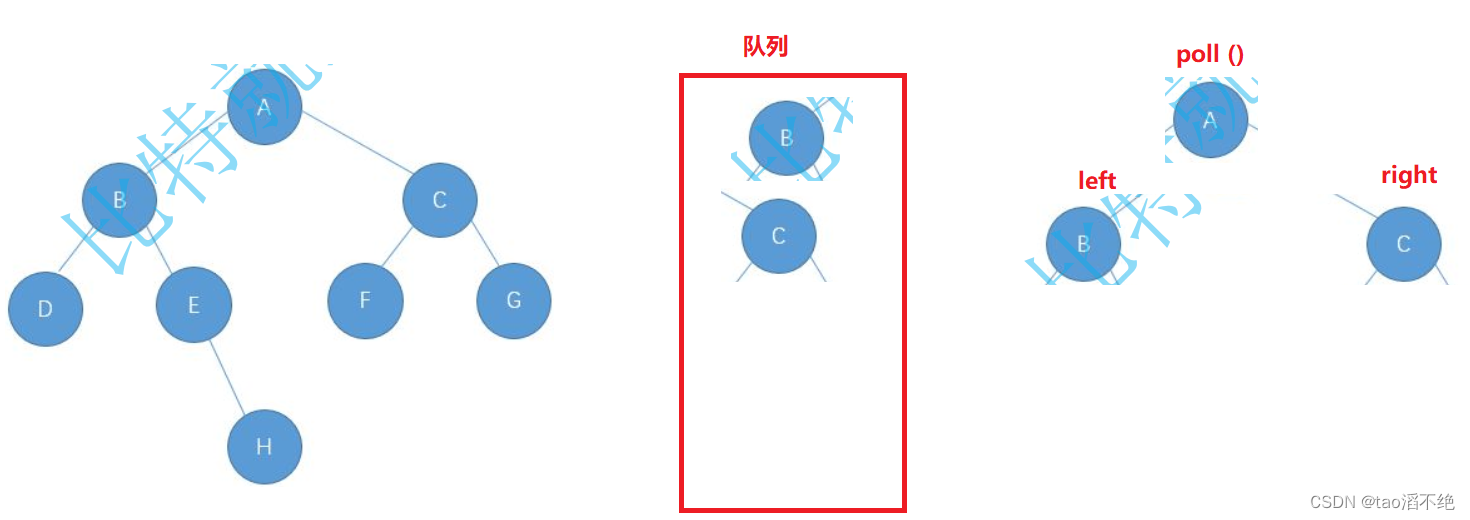
出队顶元素,次数队顶元素是B,判断B有没有左右子树,有的话分别入队列,如下图:

下一步和上面一样,如下图:
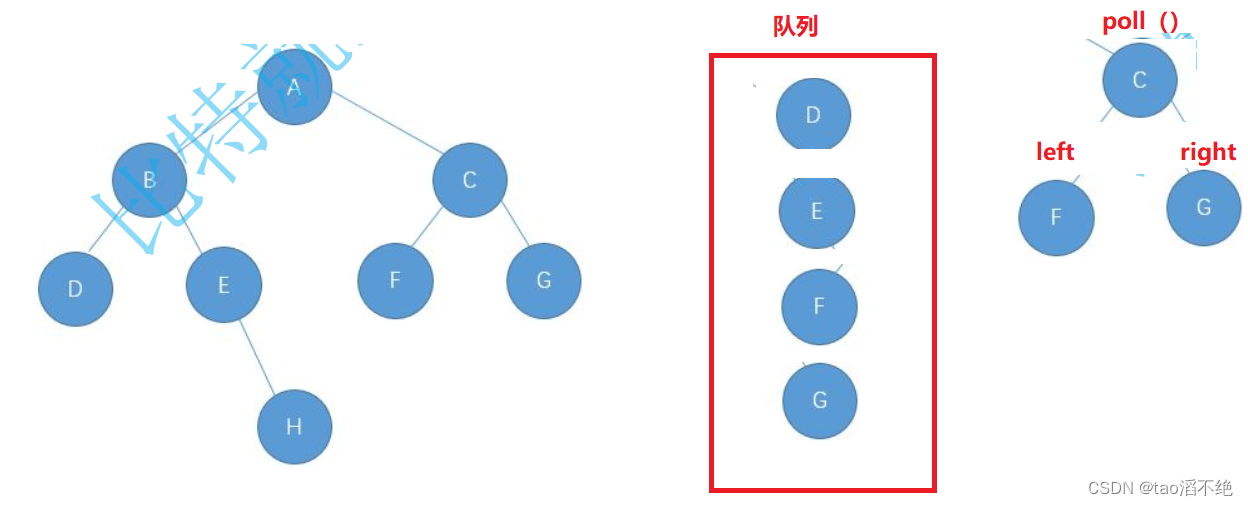
最后依次出队顶元素,再把H入队列,依次遍历,也就实现了从左到右,从上到下的遍历
代码如下:
//层序遍历void levelOrder(TreeNode root) {//没有二叉树,直接返回if(root == null) {return;}//使用队列存放二叉树的元素Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();System.out.print(ret.val + " ");if(ret.left != null) {queue.offer(ret.left);}if(ret.right != null) {queue.offer(ret.right);}}}
执行效果如下:
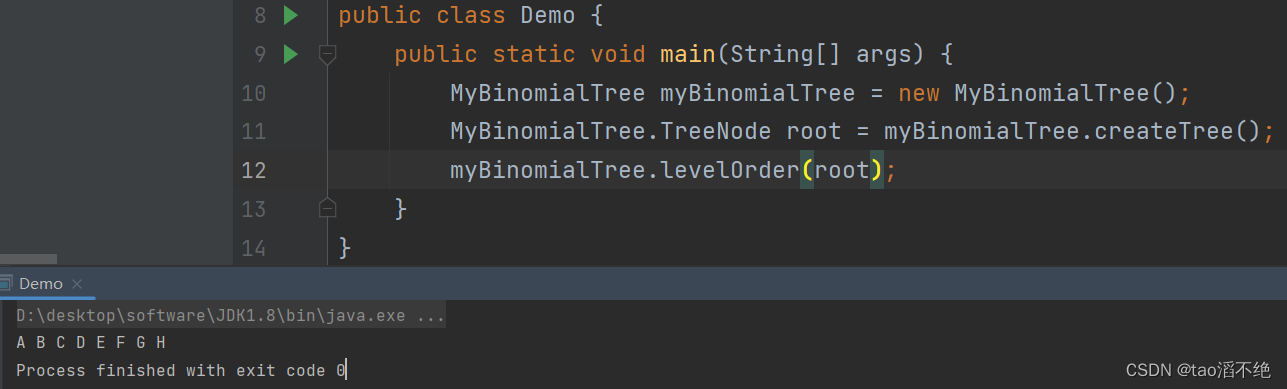
和预期结果一样。
(11)isCompleteTree
此方法是判断一棵树是不是完全二叉树,完全二叉树,即除叶子节点外,其他节点的度都为2,如下图就是完全二叉树。

但是下面的图不是完全二叉树,也是createTree方法创建的二叉树

要判断二叉树是否为完全二叉树,可以里队列,第一步骤是把二叉树层序遍历一遍:一开始把根节点root入队列,判断循环的结束条件就是队列不为空,然后找当前节点的左右子树,当前节点不为null,它的左右子树就分别存进队列,为null就直接跳出循环。这样,如果队列里有节点,即不为空的元素,则该节点不是完全二叉树,如果该队列里全是null,则是完全二叉树。因为层序遍历,如果是完全二叉树,则最后一层节点遍历完后,队列存放的元素都为null,否则不是,如图:

第二步骤是把队列里所有元素都检查一遍,如果有不为null的元素,就返回false,全为null就返回true。
代码如下:
// 判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root) {if(root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();if(ret != null) {queue.offer(ret.left);queue.offer(ret.right);}else {break;}}while (!queue.isEmpty()) {TreeNode ret = queue.peek();if(ret == null) {queue.poll();} else {return false;}}return true;}使用有H节点的的createTree方法,执行效果如下:


使用没有H节点的的createTree方法,执行效果如下:

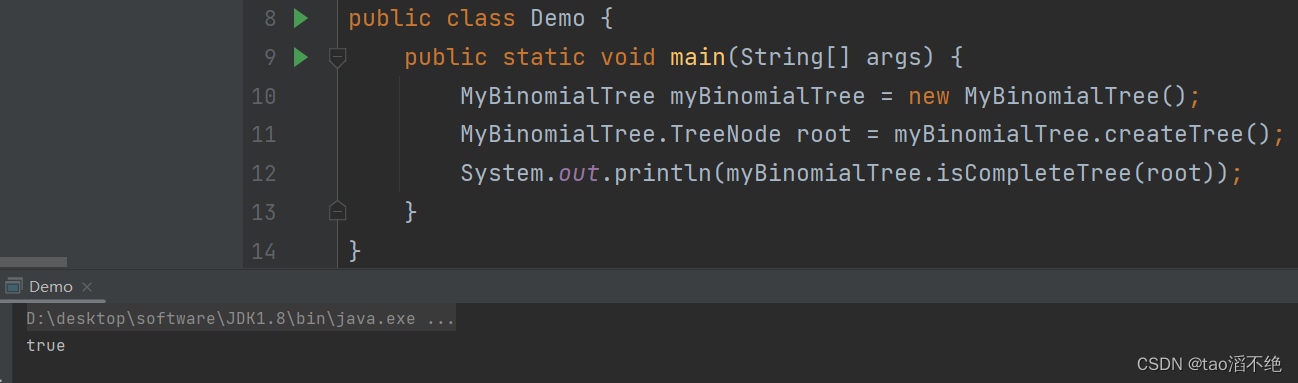
符合我们的预期效果。
三、最终代码
public class MyBinomialTree {static class TreeNode {char val;TreeNode left;TreeNode right;public TreeNode(char val) {this.val = val;}}//创建一个二叉树TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;//E.right = H;C.left = F;C.right = G;return A;}// 前序遍历void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}// 中序遍历 -》 左根右void inOrder(TreeNode root){if(root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}// 后序遍历 -》 左右根void postOrder(TreeNode root){if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}public static int count1 = 0;int size1(TreeNode root) {if(root == null) {return 0;}if(root != null) {count1++;}size1(root.left);size1(root.right);return count1;}// 获取树中节点的个数int size(TreeNode root) {if(root == null) {return 0;}return size(root.left) + size(root.right) + 1;}public static int count2 = 0;// 获取叶子节点的个数int getLeafNodeCount(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {count2++;}getLeafNodeCount(root.left);getLeafNodeCount(root.right);return count2;}// 子问题思路-求叶子结点个数int getLeafNodeCount1(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return getLeafNodeCount1(root.left) + getLeafNodeCount1(root.right);}// 获取第K层节点的个数int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}if(k == 1) {return 1;}return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);}// 获取二叉树的高度int getHeight(TreeNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null) {return 1;}return Math.max(getHeight(root.left), getHeight(root.right)) + 1;}// 检测值为value的元素是否存在TreeNode find(TreeNode root, char val) {if(root == null) {return null;}if(root.val == val) {return root;}TreeNode ret1 = find(root.left, val);if(ret1 != null) {return ret1;}TreeNode ret2 = find(root.right, val);if(ret2 != null) {return ret2;}return null;}//层序遍历void levelOrder(TreeNode root) {//没有二叉树,直接返回if(root == null) {return;}//使用队列存放二叉树的元素Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();System.out.print(ret.val + " ");if(ret.left != null) {queue.offer(ret.left);}if(ret.right != null) {queue.offer(ret.right);}}}// 判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root) {if(root == null) {return true;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {TreeNode ret = queue.poll();if(ret != null) {queue.offer(ret.left);queue.offer(ret.right);}else {break;}}while (!queue.isEmpty()) {TreeNode ret = queue.peek();if(ret == null) {queue.poll();} else {return false;}}return true;}
}
都看到这了,点个赞再走吧,谢谢谢谢!
相关文章:

数据结构 模拟实现二叉树(孩子表示法)
目录 一、二叉树的简单概念 (1)关于树的一些概念 (2)二叉树的一些概念及性质 定义二叉树的代码: 二、二叉树的方法实现 (1)createTree (2)preOrder (…...

Android14之解决刷机报错:Can not load Android system. Your data may be corrupt(一百七十七)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

二阶贝塞尔曲线生成弧线
概述 本文分享一个二阶贝塞尔曲线曲线生成弧线的算法。 效果 实现 1. 封装方法 class ArcLine {constructor(from, to, num 100) {this.from from;this.to to;this.num num;return this.getPointList();}getPointList() {const { from, to } thisconst ctrlPoint thi…...
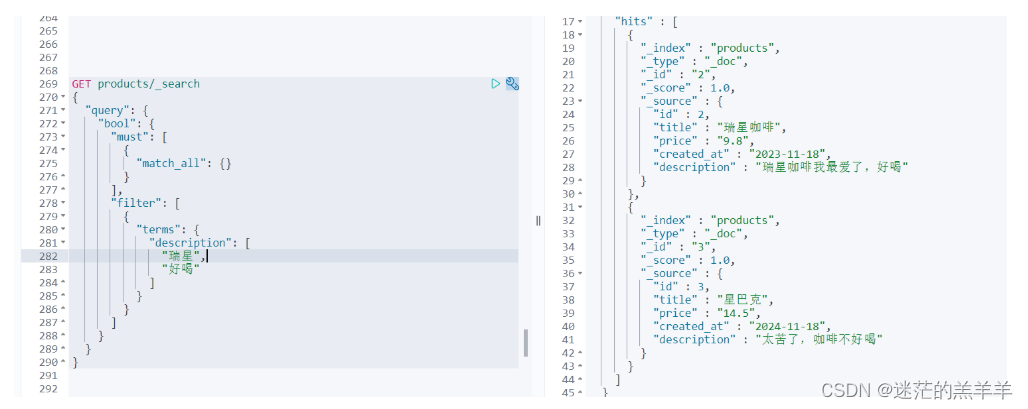
FilterQuery过滤查询
ES中的查询操作分为两种:查询和过滤。查询即是之前提到的query查询,它默认会计算每个返回文档的得分,然后根据得分排序。而过滤只会筛选出符合条件的文档,并不计算得分,并且可以缓冲记录。所以我们在大范围筛选数据时&…...

java多线程(并发)夯实之路-线程池深入浅出
线程池 Thread Pool:线程池,存放可以重复使用的线程(消费者) Blocking Queue:阻塞队列,存放等待执行的任务(生产者) poll方法(有时限地获取任务)相对take注…...

数据库-列的类型-字符串char类型
char 和 varchar 类型 char 类型懂得都懂就是固定的字符串类型 char (maxLen) 例如 char(5) 这个长度为5 但插入数据‘a’时 是5 插入abc 也是5 即使插满固定 就像C/C语言里 char 字符数组一样 char str[64]; maxLen255 哈哈最多有255个字符多了我认为你是错误 varchar…...

大话 JavaScript(Speaking JavaScript):第二十一章到第二十五章
第二十一章:数学 原文:21. Math 译者:飞龙 协议:CC BY-NC-SA 4.0 Math对象用作多个数学函数的命名空间。本章提供了一个概述。 数学属性 Math的属性如下: Math.E 欧拉常数(e) Math.LN2 2 …...

ICMP协议
ICMP协议是网络层协议, 利用ICMP协议可以实现网络中监听服务和拒绝服务,如 ICMP重定向的攻击。 一、ICMP基本概念 1、ICMP协议 ICMP是Internet控制报文协议,用于在IP主机、路由器之间传递控制消息,控制消息指网络通不通、主机是…...
环信服务端下载消息文件---菜鸟教程
前言 在服务端,下载消息文件是一个重要的功能。它允许您从服务器端获取并保存聊天消息、文件等数据,以便在本地进行进一步的处理和分析。本指南将指导您完成环信服务端下载消息文件的步骤。 环信服务端下载消息文件是指在环信服务端上,通过调…...
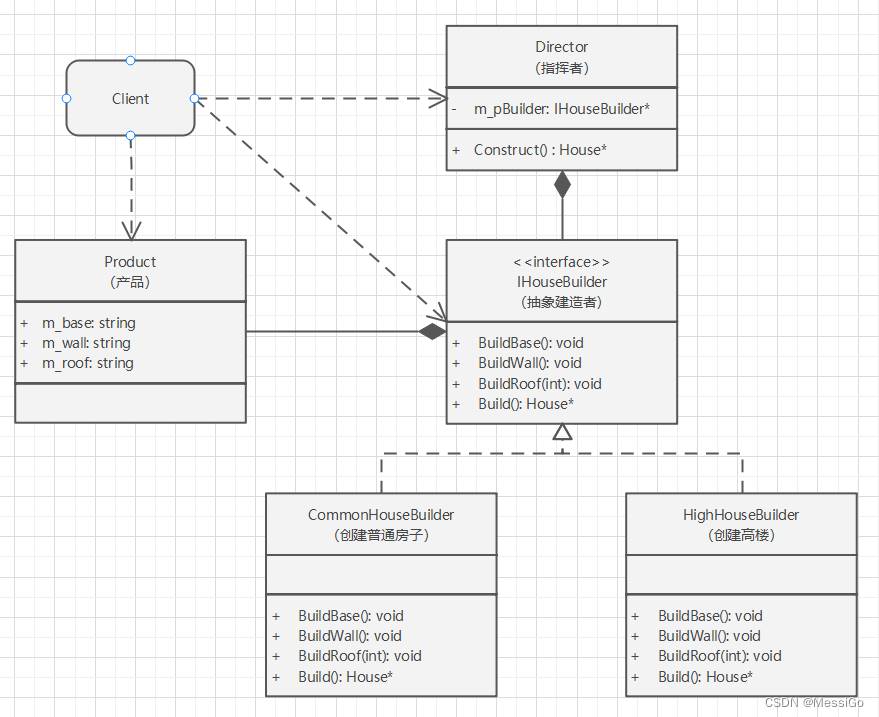
创建型模式 | 建造者模式
一、建造者模式 1、原理 建造者模式又叫生成器模式,是一种对象的构建模式。它可以将复杂对象的建造过程抽象出来,使这个抽象过程的不同实现方法可以构造出不同表现(属性)的对象。创建者模式是一步一步创建一个复杂的对象…...

MVC设计模式
在当今的软件开发领域,MVC(Model-View-Controller)设计模式已经成为了一种广泛使用的架构模式。它为应用程序提供了一种结构化的方法,将数据、用户界面和业务逻辑分开,从而使得应用程序更易于维护、扩展和重用。 一、…...
 ERROR: CreateProcessEntryCommon:493: chdir 错误解决)
WSL (2103) ERROR: CreateProcessEntryCommon:493: chdir 错误解决
[TOC](WSL (2103) ERROR: CreateProcessEntryCommon:493: chdir 错误解决) 1. 错误信息 <3>WSL (2103) ERROR: CreateProcessEntryCommon:493: chdir(/mnt/d/Program Files/PowerShell/7) failed 52. 解决方法 wsl --shutdownwslrefer: https://github.com/microsoft/…...
【二、自动化测试】为什么要做自动化测试?哪种项目适合做自动化?
自动化测试是一种软件测试方法,通过编写和使用自动化脚本和工具,以自动执行测试用例并生成结果。 自动化旨在替代手动测试过程,提高测试效率和准确性。 自动化测试可以覆盖多种测试类型,包括功能测试、性能测试、安全测试等&…...
)
用ChatGPT来造一个ChatGPT:计算机领域智能问答系统实践(2)
在PHP语言中,你可以使用MySQL数据库来存储知识库,并使用PHP来实现系统的逻辑。以下是一个简单的示例: 创建数据库表: 首先,创建一个名为 computer_knowledge 的表来存储计算机知识。可以使用以下SQL语句:…...

Ubuntu开机自动挂载硬盘
前言: 因为我的电脑是WIN10 Ubuntu18.04双系统,且两个系统都装在C盘上,而D盘作为数据和代码存储盘,经常会开机就被访问,例如上一次关机前用VS Code访问D盘代码,然后下一次开机的时候打开VSCode发现打不开…...

vue3基础:单文件组件介绍
介绍 Vue 的单文件组件 (即 *.vue 文件,简称 SFC,全称是single file component) 是一种特殊的文件格式,使我们能够将一个 Vue 组件的模板、逻辑与样式封装在单个文件中。下面是一个单文件组件的示例: <script> export def…...

OCR字符识别:开始批量识别身份证信息
身份证信息批量识别OCR是一项解决方案,它能够将身份证照片打包成zip格式或通过URL地址进行提交,并能够识别照片中的文本信息。最终,用户可以将识别结果生成为excel文件进行下载。 API接口功能: 1. 批量识别:支持将多…...
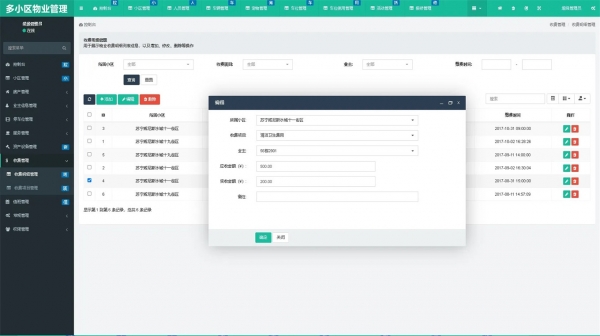
php多小区智慧物业管理系统源码带文字安装教程
多小区智慧物业管理系统源码带文字安装教程 运行环境 服务器宝塔面板 PHP 7.0 Mysql 5.5及以上版本 Linux Centos7以上 统计分析以小区为单位,统计如下数据:小区总栋数、小区总户数、小区总人数、 小区租户数量、小区每月收费金额统计、小区车位统计、小…...
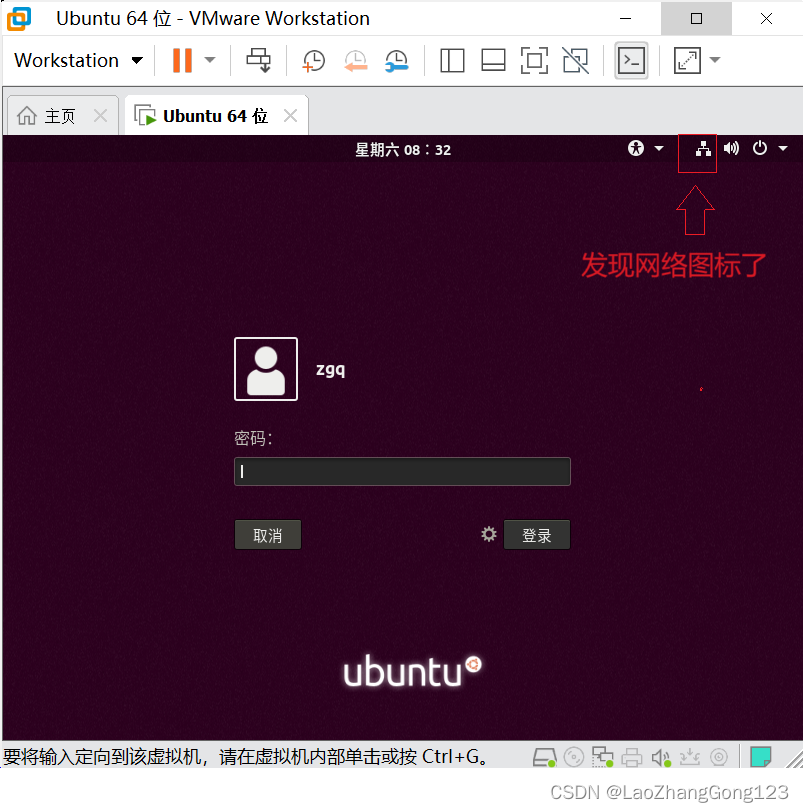
解决虚拟机的网络图标不见之问题
在WIN11中,启动虚拟机后,发现网络图标不见了,见下图: 1、打开虚拟机终端 输入“sudo server network-manager stop”,停止网络管理器 输入“cd /回车” , 切换到根目录 输入“cd var回车” ,…...

【Spring类路径Bean定义信息扫描】
Spring类路径Bean定义信息扫描 1. ClassPathBeanDefinitionScanner作用2. 类声明3. 属性4. 构造器5. 扫描方法6. 真正扫描方法7. postProcessBeanDefinition8. 注册bean定义 1. ClassPathBeanDefinitionScanner作用 扫描类路径下的类注册为bean定义。2. 类声明 public class …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
