动手学深度学习【1】——线性回归
动手学深度学习网址:动手学深度学习
注:本部分只对基础知识进行简单的介绍并附上完整的代码实现,更多内容可参考上述网址。
简述
需要的准备知识
- 数学的偏导
- 线性代数
线性模型
回归是能为一个或多个自变量与因变量之间关系建模的一类方法。 在自然科学和社会科学领域,回归经常用来表示输入和输出之间的关系。
线性回归基于几个简单的假设: 首先,假设自变量x和因变量y之间的关系是线性的, 即y可以表示为中元素的x加权和,这里通常允许包含观测值的一些噪声; 其次,我们假设任何噪声都比较正常,如噪声遵循正态分布。
给定一个数据集,线性回归的目标是寻找模型的权重w和偏差b。公式为:

将权重放到一个向量里面,变成:

损失函数
使用平方误差:

其中y是真实的数据。
将上式展开,为:

最终的目标就是寻找一组参数(w,b),这组参数能最小化在所有训练样本上的总损失,即:

优化方法
在训练过程中需要不断优化w和b,使得最终的损失达到最小,这就需要一种优化方法,通常使用的式梯度下降方法。
对于线性回归,参数更新的形式为:

因为在每一次更新参数之前,我们必须遍历整个数据集。 因此,**我们通常会在每次需要计算更新的时候随机抽取一小批样本, 这种变体叫做小批量随机梯度下降。**如上图所示,其中的B就是选取的小批量样本个数,n是学习率。
将上述式子展开,为:

代码
从头开始实现线性回归
1.生成数据集
我们生成一个包含1000个样本的数据集, 每个样本包含从标准正态分布中采样的2个特征。
import torch
import random
from d2l import torch as d2l
# 生成数据集
def generate_data(w,b,num_examples):# 生成正太分布的数据X = torch.normal(0,1,(num_examples,len(w)))# 进行矩阵乘法y = torch.matmul(X,w) + by += torch.normal(0,0.01,y.shape)return X,y.reshape((-1,1))
# 真实的w
true_w = torch.tensor([2,-3.4])
# 真实的b
true_b = 4.2
# features shape: N * len(W)
# lables shape: N
features,labels = generate_data(true_w,true_b,1000)
print('features:',features[0],'\nlabel:',labels[0])
# 展示生成的数据
d2l.set_figsize()
d2l.plt.scatter(features[:,1].detach().numpy(),labels.detach().numpy(),1)
2.读取数据操作
定义一个data_iter函数, 该函数接收批量大小、特征矩阵和标签向量作为输入,生成大小为batch_size的小批量。
# 小批量读取数据集
def data_iter(batch_size,features,lables):# 获取第一维的大小num_examples = len(features)indices = list(range(num_examples))# 打乱顺序random.shuffle(indices)for i in range(0,num_examples,batch_size):batch_indices = torch.tensor(indices[i:min(i+batch_size,num_examples)])yield features[batch_indices],labels[batch_indices]
# 调用该函数
# 小批量大小为10
batch_size = 10
for X,y in data_iter(batch_size,features,batch_size):print(X,'\n',y)break
3.定义模型相关部分
(1)初始化参数
我们通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重, 并将偏置初始化为0。
(2)定义模型
使用wx+b形式。
(3)损失函数
使用平方损失函数
(4)优化方法
在每一步中,使用从数据集中随机抽取的一个小批量,然后根据参数计算损失的梯度。 接下来,朝着减少损失的方向更新我们的参数。 每一步更新的大小由学习速率lr决定。 因为我们计算的损失是一个批量样本的总和,所以我们用批量大小(batch_size) 来规范化步长,这样步长大小就不会取决于我们对批量大小的选择。
# 初始化模型参数
def init_params():# w服从均值为0,方差为0.01的正太分布,大小为(2,1)w = torch.normal(0,0.01,(2,1),requires_grad = True)b = torch.zeros(1,requires_grad = True)return w,b
# 定义模型
def linear_reg(X,w,b):# wx + breturn torch.matmul(X,w) + b# 定义损失函数
def squared_loss(y_pred,y):return (y_pred - y.reshape(y_pred.shape)) ** 2 / 2# 定义优化算法
def sgd(params,lr,batch_size):# 使梯度计算disablewith torch.no_grad():for param in params:param -= lr * param.grad / batch_size# 手动将梯度设置成 0 ,在下一次计算梯度的时候就不会和上一次相关了param.grad.zero_()
4.训练模型
执行以下循环:
- 初始化参数
- 重复以下训练,直到完成
- 计算梯度 (l.sum().backward())
- 更新参数(sgd)
# 训练
# 学习率
lr = 0.02
# 迭代次数
num_epoches = 3
net = linear_reg
loss = squared_loss
w,b = init_params()
for epoch in range(num_epoches):for X,y in data_iter(batch_size,features,labels):l = loss(net(X,w,b),y)# 后向传播计算梯度l.sum().backward()sgd([w,b],lr,batch_size)with torch.no_grad():train_l = loss(net(features,w,b),labels)print(f'epoch {epoch + 1},loss {float(train_l.mean())}')print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
线性回归的框架实现
# 简洁实现
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
from torch import nntrue_w = torch.tensor([2,-3.4])
true_b = 4.2
# 生成数据集
features,labels = d2l.synthetic_data(true_w,true_b,1000)def load_dataset(data_arrs,batch_size,is_train = True):dataset = data.TensorDataset(*data_arrs)return data.DataLoader(dataset,batch_size,shuffle=is_train)batch_size = 10
data_iter = load_dataset((features,labels),batch_size)
# iter构造迭代器
next(iter(data_iter))# 定义模型
net = nn.Sequential(nn.Linear(2,1))
# 初始化参数,注意上面使用的是nn.Sequential,创造的是一个序列,所以net[0]表示我们的网络
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)
# 损失函数
loss = nn.MSELoss()
# 优化算法
trainer = torch.optim.SGD(net.parameters(),lr = 0.03)
# 训练
num_epoches = 3
for epoch in range(num_epoches):for X,y in data_iter:l = loss(net(X),y)# 将梯度重置为0trainer.zero_grad()# 计算梯度l.backward()# 更新所有的参数trainer.step()l = loss(net(features),labels)print(f'epch {epoch + 1} loss {l:f}')
w = net[0].weight.data
b = net[0].bias.data
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
相关文章:

动手学深度学习【1】——线性回归
动手学深度学习网址:动手学深度学习 注:本部分只对基础知识进行简单的介绍并附上完整的代码实现,更多内容可参考上述网址。 简述 需要的准备知识 数学的偏导线性代数 线性模型 回归是能为一个或多个自变量与因变量之间关系建模的一类方…...

Html 相关知识
Html 相关知识 DOM 文档对象模型 (DOM) 是 HTML 和 XML 文档的编程接口。它提供了对文档的结构化的表述,并定义了一种方式可以使从程序中对该结构进行访问,从而改变文档的结构,样式和内容。DOM 将文档解析为一个由节点和对象(包…...

【冲刺蓝桥杯的最后30天】day1
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始逐渐恢复更新状态,正在备战蓝桥杯的小伙伴可以支持一下哦!…...

c++泛型编程与模板-01函数模板
函数模板的定义 所谓函数模板,实际就是写一个通用函数,返回值和参数的类型都是可变的,用一个特定格式的变量来指定,然后调用此函数的时候,编译器会根据参数的数据类型自动推导出类型,从而达到函数再不同的…...
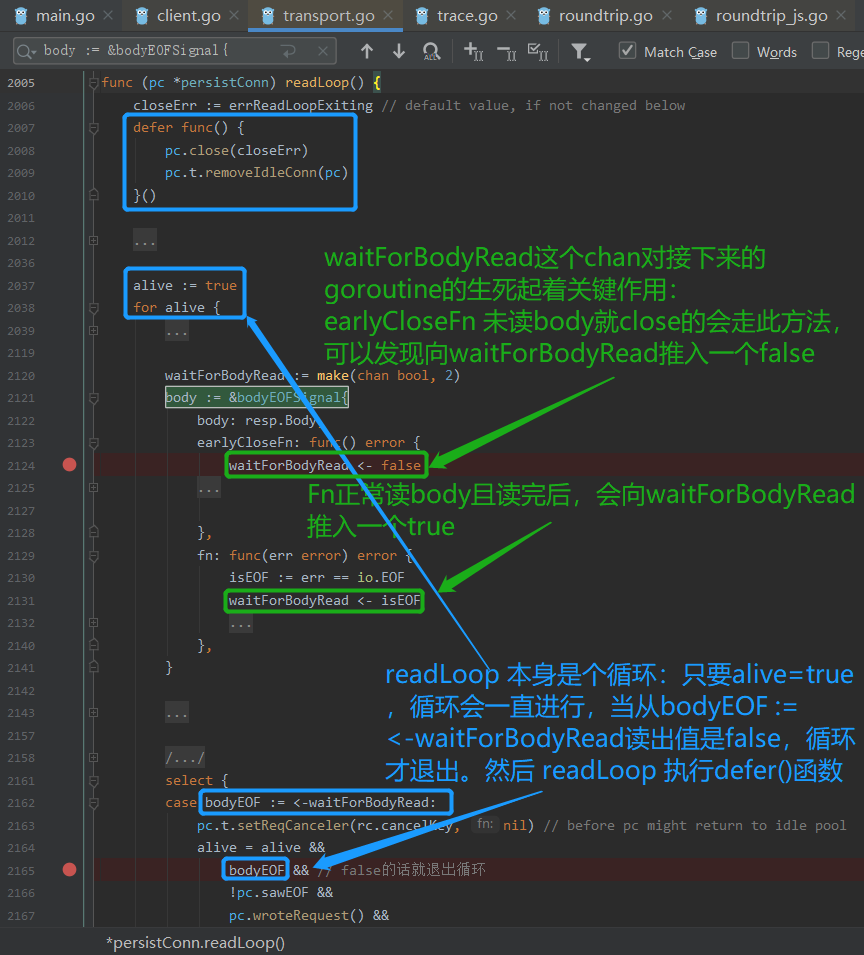
Golang http请求忘记调用resp.Body.Close()而导致的协程泄漏问题(含面试常见协程泄漏相关测试题)
参考: 知乎:别因为忘记close你的httpclient,造成goroutine泄漏 CSDN:resp.Body.Close() 引发的内存泄漏goroutine个数 先来看几道题,想一想最终的输出结果是多少呢? package mainimport ("fmt"…...

进程信号生命周期详解
信号和信号量半毛钱关系都没有! 每个信号都有一个编号和一个宏定义名称,这些宏定义可以在signal.h中找到,例如其中有定 义 #define SIGINT 2 查看信号的机制,如默认处理动作man 7 signal SIGINT的默认处理动作是终止进程,SIGQUIT的默认处理…...

2023-03-03干活小计
今天见识了 归一化的重要性:归一化 不容易爆炸 深度了解了学习率:其实很多操作 最后的结果都是改变了lr 以房价预测为例:一个点一个点更新 比较 矩阵的更新: 为什么小批量梯度下降 优于随机梯度下降 优于批量梯度下降ÿ…...

操作系统结构
随着操作系统的不断增多和代码规模的不断扩大,提供合理的结构对提升操作系统的安全与可靠性来说变得尤为重要。 1.分层法 指将操作系统分为若干层,最低层位硬件,最高层为用户接口,每层只能调用紧邻它的低层的功能和服务(类似于计…...

[SSD科普] 固态硬盘物理接口SATA、M.2、PCIe常见疑问,如何选择?
前言犹记得当年Windows 7系统体验指数中,那5.9分磁盘分数,在其余四项的7.9分面前,似乎已经告诉我们机械硬盘注定被时代淘汰。势如破竹的SSD固态硬盘,彻底打破了温彻斯特结构的机械硬盘多年来在电脑硬件领域的统治。SSD数倍于HDD机…...
【Java学习笔记】3.Java 基础语法
Java 基础语法 一个 Java 程序可以认为是一系列对象的集合,而这些对象通过调用彼此的方法来协同工作。下面简要介绍下类、对象、方法和实例变量的概念。 对象:对象是类的一个实例,有状态和行为。例如,一条狗是一个对象ÿ…...

Python基础学习6——if语句
基本概念 if语句为条件判断语句,用来判断if后面的语句是真是假。if的用途有很多,比如作为条件测试可以判断两数是否相等与不等、进行数值笔记等等。例子如下: Lego_price (599, 799, 898) if Lego_price[0] 599:print("Correct!&quo…...
有免费的PDF转Word吗?值得收藏的7个免费 PDF转Word工具请收好
PDF 和 DOC 是人们在工作中广泛使用的两种最流行的文档格式。PDF 是 Adobe 的便携式文档格式,DOC 是 Microsoft 的 Word 文档格式。PDF 是一种更安全可靠的文件格式,因为它很难编辑 PDF 文件,但是有一些称为 PDF 编辑器的工具可用于编辑 PDF …...
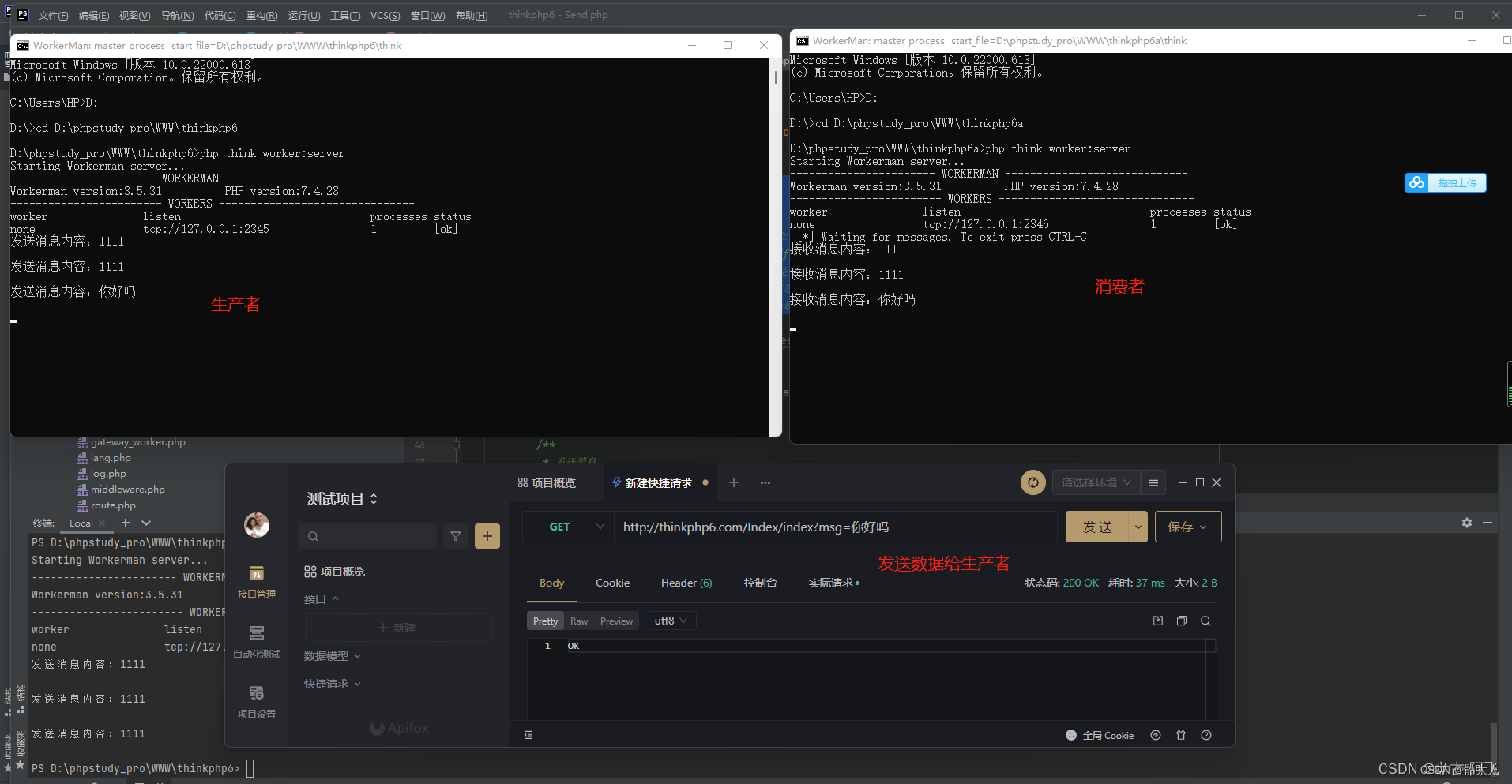
Thinkphp6使用RabbitMQ消息队列
Thinkphp6连接使用RabbitMQ(不止tp6,其他框架对应改下也一样),如何使用Docker部署RabbitMQ,在上一篇已经讲了->传送门<-。 部署环境 开始前先进入RabbitMQ的web管理界面,选择Queues菜单,点…...

小成本互联网创业怎么做?低成本创业的方法分享
多数人都会有想法创业,尤其是在互联网上面创业,很多人看到了商机,但是因为成本的原因又放弃了,实际上,小成本也可以互联网创业!那么,小成本互联网创业怎么做?低成本创业的方法在这里…...

六、栈、栈的相关问题
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、栈 1.栈概述 2.栈的实现 2.1 栈的API 2.2 栈的实现 二、栈的括号匹配问题 1.问题描述 2.代码实现 三、逆波兰表达式求值问题 1.问题描述 2.代码 总结 前言 提…...

Java安全停止线程
Thread 类虽提供了一个 stop() 方法(已经被废弃),但由于 stop() 方法强制终止一个正在执行的线程,可能会造成数据不一致的问题,所以在生产环境中最好不要使用。 场景: 由于一些操作需要轮询处理ÿ…...
12 readdir 函数
前言 在之前 ls 命令 中我们可以看到, ls 命令的执行也是依赖于 opendir, readdir, stat, lstat 等相关操作系统提供的相关系统调用来处理业务 因此 我们这里来进一步看一下 更细节的这些 系统调用 我们这里关注的是 readdir 这个函数, 入口系统调用是 getdents 如下调试…...

Windows环境搭建Android开发环境-Android Studio/Git/JDK
Windows环境搭建Android开发环境-Android Studio/Git/JDK 因为休假回来后公司的开发环境由Ubuntu变为了Windows,所以需要重新配置一下开发环境。 工作多年第一次使用Windows环境进行开发工作,作次记录下来。 一、 Git安装 1.1git 标题软件下载 网址&…...

全国爱耳日丨听力受损严重有哪些解决办法
——【科学爱耳护耳,实现主动健康】随着数码电子设备使用越来越方便、日常使用时间越来越长,听力障碍、患上耳道疾病一系列问题也接踵而至,在当下我们必须重视听力健康,采取更科学的听音方式,保护听力健康,…...

【抽水蓄能电站】基于粒子群优化算法的抽水蓄能电站的最佳调度方案研究(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
