法线变换矩阵的推导
背景
在冯氏光照模型中,其中的漫反射项需要我们对法向量和光线做点乘计算。
从顶点着色器中读入的法向量数据处于模型空间,我们需要将法向量转换到世界空间,然后在世界空间中让法向量和光线做运算。这里便有一个问题,如何将法线从当前的模型空间变换到世界空间?
首先,法向量只是一个方向向量,不能表达空间中的特定位置。同时,法向量没有齐次坐标(顶点位置中的w分量)。这意味着,位移不应该影响到法向量。因此,如果我们打算把法向量乘以一个模型矩阵,我们就要从矩阵中移除位移部分,只选用模型矩阵左上角3×3的矩阵(注意,我们也可以把法向量的w分量设置为0,再乘以4×4矩阵;这同样可以移除位移)。对于法向量,我们只希望对它实施缩放和旋转变换。
其次,如果模型矩阵执行了不等比缩放,顶点的改变会导致法向量不再垂直于表面了。因此,我们不能用这样的模型矩阵来变换法向量。下面的图展示了应用了不等比缩放的模型矩阵对法向量的影响:

当我们应用一个不等比缩放时(注意:等比缩放不会破坏法线,因为法线的方向没被改变,仅仅改变了法线的长度,而这很容易通过标准化来修复),法向量就不会再垂直于对应的表面了,这样光照就会被破坏。
修复这个行为的诀窍是使用一个为法向量专门定制的模型矩阵。这个矩阵称之为法线矩阵(Normal Matrix),它使用了一些线性代数的操作来移除对法向量错误缩放的影响。
推导过程
为了将一个顶点从模型空间转换到世界空间,我们可以乘上一个模型矩阵model,包含物体的移动、旋转、缩放信息。在shader中的代码如下:
FragPos = vec3(model * vec4(aPos, 1.0));
对于一个向量,正如上面的图展示的一样,我们不能简单乘上model矩阵。如果乘上model矩阵,向量就不再和原来的表面切线垂直了。
我们可以定义表面切线为 T = P 2 − P 1 T = P_2 - P1 T=P2−P1,其中 P 1 , P 2 P_1,P_2 P1,P2都是表面上的顶点。当表面前线乘上model矩阵时,我们有:
m o d e l ∗ T = m o d e l ∗ P 2 − m o d e l ∗ P 1 T ′ = P 2 ′ − P 1 ′ model * T = model * P_2 - model * P_1 \\ T' = P_2' - P_1' model∗T=model∗P2−model∗P1T′=P2′−P1′
变换后的表面切线 T ′ T' T′仍然可以表示成表面上顶点的差,因此乘上model矩阵之后,表面切线不会被破坏。
对于表面上的法线 N N N,我们无法从表面上找到两个顶点来表示,但是我们知道表面法线与切线互相垂直,即
N ⋅ T = 0 N \cdot T = 0 N⋅T=0
我们假设矩阵 G G G就是可以将法线从模型空间转换到世界空间的正确矩阵,并用 M M M来表示模型矩阵model,于是有下式:
N ′ ⋅ T ′ = ( G N ) ⋅ ( M T ) = 0 N' \cdot T' = (GN)\cdot(MT) = 0 N′⋅T′=(GN)⋅(MT)=0
转化成矩阵表示的形式
( G N ) ⋅ ( M T ) = ( G N ) T ∗ ( M T ) = N T G T M T = 0 (GN)\cdot(MT) = (GN)^T*(MT) = N^TG^TMT = 0 (GN)⋅(MT)=(GN)T∗(MT)=NTGTMT=0
我们知道 N ⋅ T = N T T = 0 N\cdot T = N^TT = 0 N⋅T=NTT=0,所以如果 G T M = a I G^TM = aI GTM=aI, a a a是任意非零常数,我们便有
N ′ ⋅ T ′ = N T G T M T = N T a I T = a N T T = 0 N'\cdot T' = N^TG^TMT = N^TaIT = aN^TT = 0 N′⋅T′=NTGTMT=NTaIT=aNTT=0
由于我们不想改变法向量的模长,因此令 a = 1 a = 1 a=1,只要满足 G T M = I G^TM = I GTM=I的条件,我们就可以说 G G G是我们最终需要的矩阵,进一步计算
G T M = I ⟷ G = ( M − 1 ) T G^TM = I \longleftrightarrow G = (M^{-1})^T GTM=I⟷G=(M−1)T
最终可得,将法线从模型空间转换到世界空间的矩阵为 ( M − 1 ) T (M^{-1})^T (M−1)T。
补充说明
当模型矩阵只进行了旋转或等比缩放时,我们用这个矩阵来变换法线向量,可以得到正确的结果。
这是因为旋转矩阵和等比缩放矩阵都是正交矩阵,正交矩阵有一个属性:矩阵的转置等于矩阵的逆。
因此
M − 1 = M T → G = ( M − 1 ) T = M M^{-1} = M^T \rightarrow G = (M^{-1})^T = M M−1=MT→G=(M−1)T=M
参考
https://learnopengl-cn.github.io/02%20Lighting/02%20Basic%20Lighting/
http://www.lighthouse3d.com/tutorials/glsl-12-tutorial/the-normal-matrix/
相关文章:

法线变换矩阵的推导
背景 在冯氏光照模型中,其中的漫反射项需要我们对法向量和光线做点乘计算。 从顶点着色器中读入的法向量数据处于模型空间,我们需要将法向量转换到世界空间,然后在世界空间中让法向量和光线做运算。这里便有一个问题,如何将法线…...
React.Children.map 和 js 的 map 有什么区别?
JavaScript 中的 map 不会对为 null 或者 undefined 的数据进行处理,而 React.Children.map 中的 map 可以处理 React.Children 为 null 或者 undefined 的情况。 React 空节点:可以由null、undefined、false、true创建 import React from reactexport …...

13.Kubernetes部署Go应用完整流程:从Dockerfile到Ingress发布完整流程
本文以一个简单的Go应用Demo来演示Kubernetes应用部署的完整流程 1、Dockerfile多阶段构建 Dockerfile多阶段构建 [root@docker github]# git clone https://gitee.com/yxydde/http-dump.git [root@docker github]# cd http-dump/ [root@docker http-dump]# cat Dockerfile …...
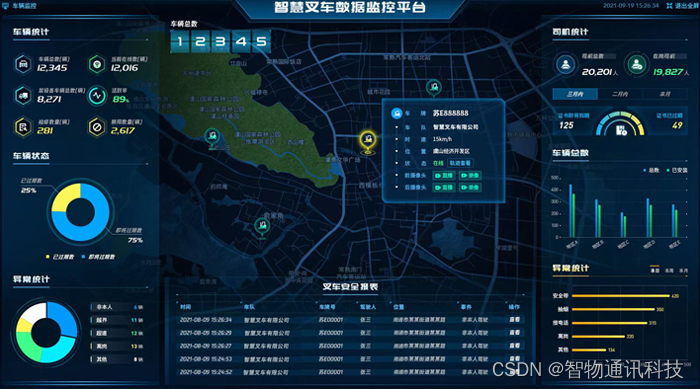
叉车车载终端定制_基于MT6762安卓核心板的车载终端设备方案
叉车车载终端是一款专为叉车车载场景设计的4英寸Android车载平板电脑。它采用了高能低耗的8核ARM架构处理器和交互开放的Android 12操作系统,算力表现强大。此外,该产品还具备丰富的Wi-Fi-5、4G LTE和蓝牙等通讯功能,可选配外部车载蘑菇天线&…...
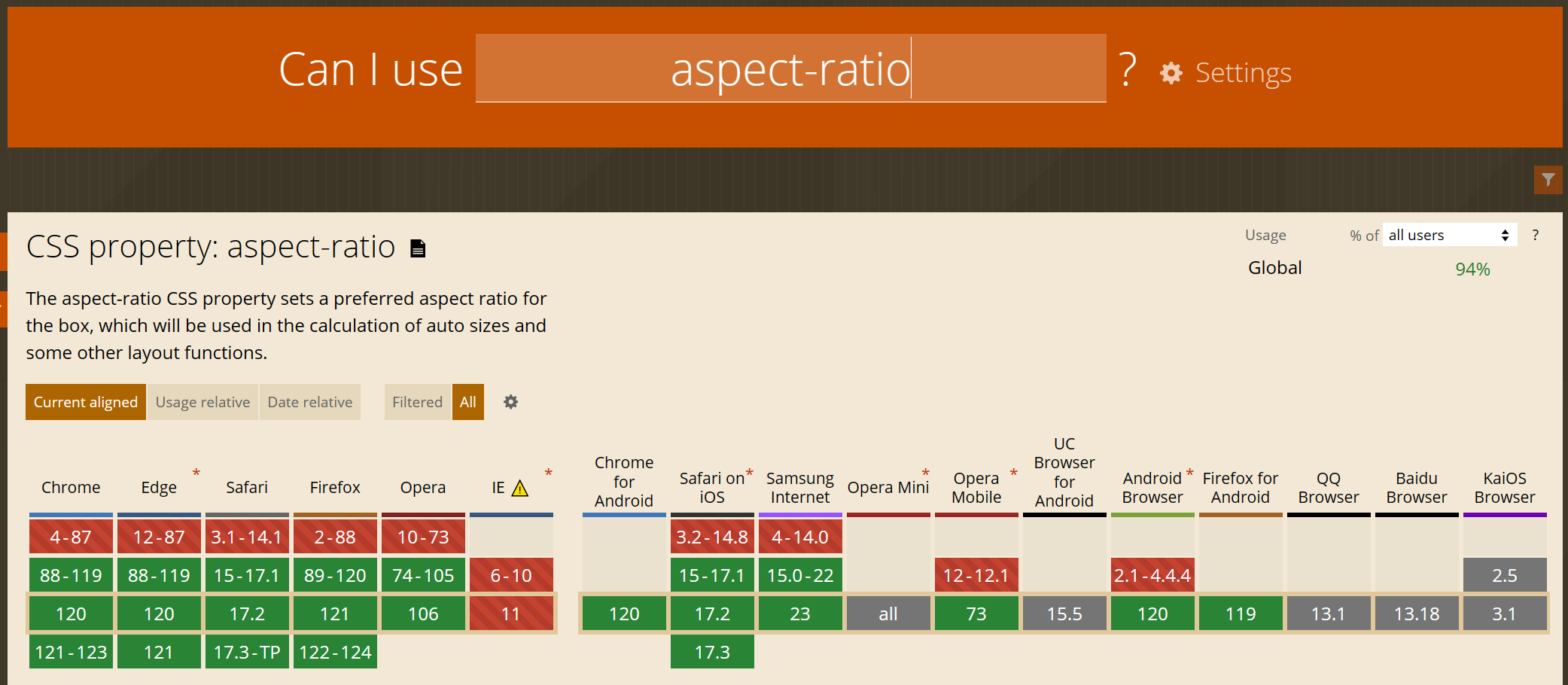
【CSS】保持元素宽高比
保持元素的宽高比,在视频或图片展示类页面是一个重要功能。 本文介绍其常规的实现方法。 实现效果 当浏览器视口发生变化时,元素的尺寸随之变化,且宽高比不变。 代码实现 我们用最简单的元素结构来演示,实现宽高比为4…...

使用 Docker 和 Diffusers 快速上手 Stable Video Diffusion 图生视频大模型
本篇文章聊聊,如何快速上手 Stable Video Diffusion (SVD) 图生视频大模型。 写在前面 月底计划在机器之心的“AI技术论坛”做关于使用开源模型 “Stable Diffusion 模型” 做有趣视频的实战分享。 因为会议分享时间有限,和之前一样,比较简…...

C++ namespace高级用法
高级用法 C++中的命名空间(namespace)是一种用于组织代码的机制,它可以帮助避免命名冲突,并使代码更加清晰和易于维护。以下是C++命名空间的一些高级用法: 嵌套命名空间:命名空间可以嵌套在其他命名空间中,形成一个层次结构。嵌套命名空间可以进一步细化命名空间,使其更…...

如何允许远程访问 MySQL
前些天发现了一个人工智能学习网站,通俗易懂,风趣幽默,最重要的屌图甚多,忍不住分享一下给大家。点击跳转到网站。 如何允许远程访问 MySQL 现在许多网站和应用程序一开始的 Web 服务器和数据库后端都托管在同一台计算机上。随着…...

PostgreSQL认证考试PGCA、PGCE、PGCM
PostgreSQL认证考试PGCA、PGCE、PGCM 【重点!重点!重点!】PGCA、PGCE、PGCM 直通车快速下正,省心省力,每2个月一次考试 PGCE考试通知 (2024) 一、考试概览 (一) 报名要…...
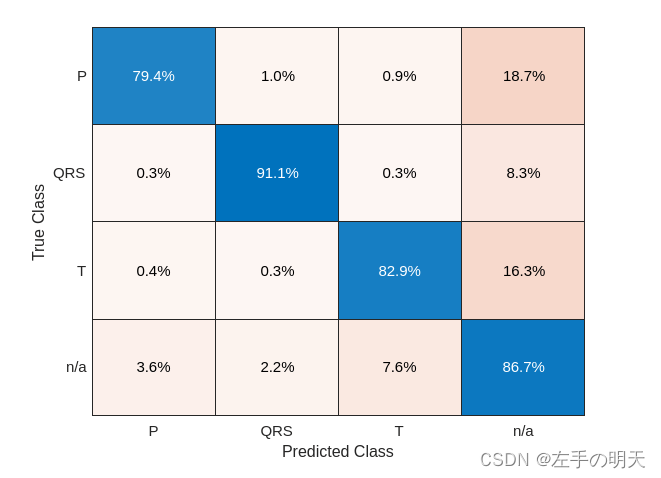
Matlab深度学习进行波形分割(二)
🔗 运行环境:Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 🔐#### 防伪水印——左手の明天 ####🔐 💗 大家…...

Markdown高级用法——mermaid
Markdown高级用法——mermaid 起初是写文章,其中有时序图流程图等一般是processOn或者draw.io画截图粘过去的,工作中又是腾讯文档,上面也能画图,但假如我笔记软件用语雀之类的又要把一张图反复粘贴,浪费内存ÿ…...

cf919Div2C题题目总结
Problem - C - Codeforces 这道题其实是一道数学题。 先看第一个变量,也就是我们要求的答案k的数量,但看k是很好确定它的限制条件的,要想均匀分成k份,n%k必须为0,有了k,我们再来看m,对于a(1)和…...

Pandas实战100例 | 案例 4: 数据选择和索引 - 选择特定的列和行
案例 4: 数据选择和索引 - 选择特定的列和行 知识点讲解 在 Pandas 中,选择数据是一个非常常见的操作。你可以选择特定的列或行,或者基于某些条件筛选数据。 示例代码 选择特定的列 # 选择单列 selected_column df[ColumnName]# 选择多列 selected…...

Netty-Netty实现自己的通信框架
通信框架功能设计 功能描述 通信框架承载了业务内部各模块之间的消息交互和服务调用,它的主要功能如下: 基于 Netty 的 NIO 通信框架,提供高性能的异步通信能力; 提供消息的编解码框架,可以实现 POJO 的序列化和反…...

【算法刷题】总结规律 算法题目第2讲 [234] 回文链表,因为深浅拷贝引出的bug
配合b站视频讲解食用更佳:https://www.bilibili.com/video/BV1vW4y1P7V7 核心提示:好几道题是处理有序数组的! 适合人群:考研/复试/面试 解决痛点:1. 刷了就忘 2.换一道相似的题就不会 学完后会输出:对每类题目的框架…...

RabbitMQ如何保证消息不丢失?
RabbitMQ如何保证消息不丢失? 消息丢失的情况 生产者发送消息未到达交换机生产者发送消息未到达队列MQ宕机,消息丢失消费者服务宕机,消息丢失 生产者确认机制 解决的问题:publisher confirm机制来避免消息发送到MQ过程中消失。…...
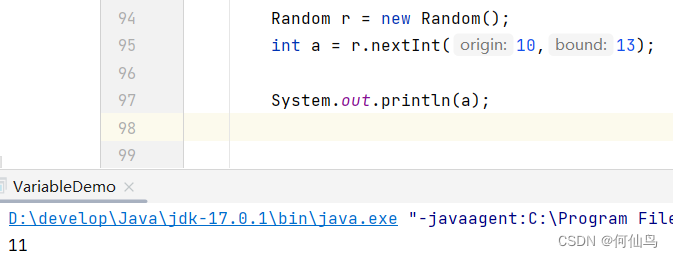
Random的使用
作用:生成伪随机数 1.导包:import java.util.Random 2.得到随机数对象:Random r new Random(); 3.调用随机数的功能获取随机数: 这里随机生成一个0-9的整数: int number r.nextInt(10); 实现指定区间的随机数&a…...
通过反射修改MultipartFile类文件名
1、背景 项目上有这样一个需求,前端传文件过来,后端接收后按照特定格式对文件进行重命名。(修改文件名需求其实也可以在前端处理的) //接口类似于下面这个样子 PosMapping("/uploadFile") public R uploadFile(List<MultipartFile> fil…...
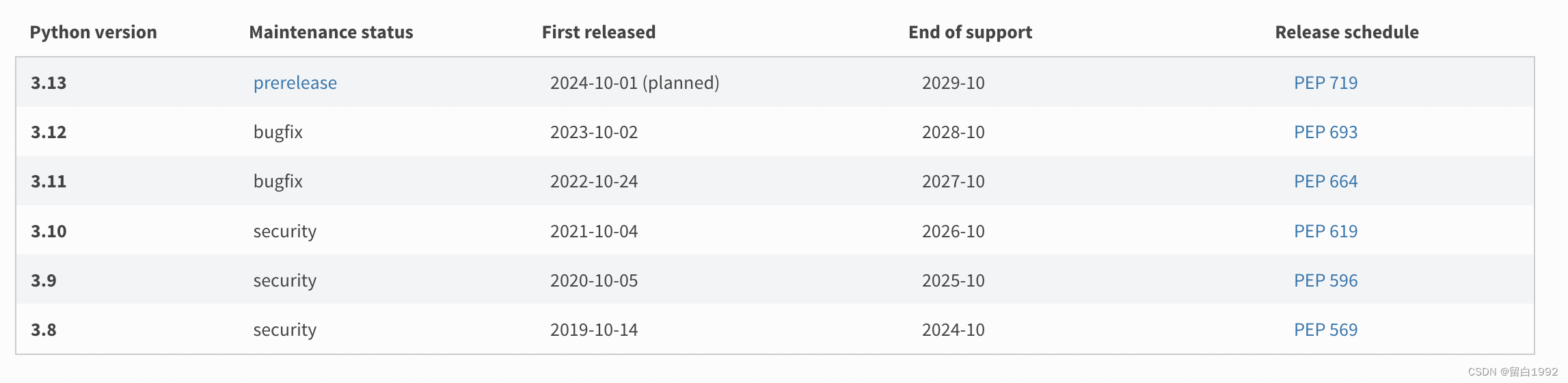
Macos下修改Python版本
MacOS下修改Python版本 安装 查看本机已安装的Python版本:where python3 ~ where python3 /usr/bin/python3 /usr/local/bin/python3 /Library/Frameworks/Python.framework/Versions/3.12/bin/python3如果没有你想要的版本,去python官网下载安装包。…...

多种采购方式下,数智化招标采购系统建设解决方案
广发证券成立于1991年,是国内首批综合类证券公司,先后于2010年和2015年在深圳证券交易所及香港联合交易所主板上市。 多年来,广发证券在竞争激烈、复杂多变的行业环境中努力开拓、锐意进取,以卓越的经营业绩、持续完善的全面风险…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...
