341. 最优贸易(dp思想运用,spfa,最短路)
341. 最优贸易 - AcWing题库
C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。
任意两个城市之间最多只有一条道路直接相连。
这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为 1 条。
C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。
但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C 国旅游。
当他得知“同一种商品在不同城市的价格可能会不同”这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚一点旅费。
设 C 国 n 个城市的标号从 1∼n,阿龙决定从 1 号城市出发,并最终在 n 号城市结束自己的旅行。
在旅游的过程中,任何城市可以被重复经过多次,但不要求经过所有 n 个城市。
阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品——水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。
因为阿龙主要是来 C 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
现在给出 n 个城市的水晶球价格,m 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。
请你告诉阿龙,他最多能赚取多少旅费。
注意:本题数据有加强。
输入格式
第一行包含 2 个正整数 n 和 m,中间用一个空格隔开,分别表示城市的数目和道路的数目。
第二行 n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n 个城市的商品价格。
接下来 m 行,每行有 33 个正整数,x,y,z,每两个整数之间用一个空格隔开。
如果 z=1,表示这条道路是城市 x 到城市 y 之间的单向道路;如果 z=2,表示这条道路为城市 x 和城市 y 之间的双向道路。
输出格式
一个整数,表示答案。
数据范围
1≤n≤100000
1≤m≤500000
1≤各城市水晶球价格≤100
输入样例:
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
输出样例:
5解析 :
本题做法有很多,可以使用分层图来处理,这里使用dp的方式处理。
状态划分:不重不漏,将状态转移所依据的状态体现出来;
fmax[i], fmin[i] 表示:路径上买和卖的分界点为 i 时,买入的最小值为fmin[i],卖出的最大值为fmax[i];
那么最终的结果就为 max{fmax[i]-fmin[i]}。
状态转移方程为:fmin[k]=min(fmin[j],……,wk),
fmax[k]的状态转移方程类似。
本质上是个dp问题,由于本题中的图可能是有环的,即dp的状态转移是环形的具有后效性,所以我们需要将其转换最短路问题进行处理(对于环形dp可查看dp专栏)
本题要有一点特别的地方是,本题边的权值在点上,而不在边上。仔细观察可以发现,本题是不能使用Dijkstra 算法的,因为从公式fmin[k]=min(fmin[j],……,wk)可以看出来如果使用Dijkstra算法,当存在环时,已经更新过的点还有可能被更新,等价于有负权边,换句话说,路径上的最小距离不单调递增。所以我们只能使用bellman_ford算法或其升级版算法spfa算法。
dp相当于求拓扑图上的最短路。spfa可以求任意图上的最短路。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
typedef pair<double, int > PDI;
typedef pair<int, int> PII;
const int N = 1e5 + 5, M = 2e6 + 5, INF = 0x3f3f3f3f;
int n, m;
int ht[N], hs[N], e[M], ne[M], idx;
int w[N], dmin[N], dmax[N];
int q[N];
int vis[N];void add(int h[], int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void spfa(int h[], int dist[], int type) {int hh = 0, tt = 1;if (type==0) {memset(dist, 0x3f, sizeof dmin);dist[1] = w[1];q[0] = 1;}else {memset(dist, 0, sizeof dmax);dist[n] = w[n];q[0] = n;}while (hh != tt) {int t = q[hh++];if (hh == N)hh = 0;vis[t] = 0;for (int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if (type == 0 && dist[j]>min(dist[t], w[j]) || type == 1 && dist[j]<max(dist[t], w[j])) {if (type == 0) {dist[j] = min(dist[t], w[j]);}else {dist[j] = max(dist[t], w[j]);}if (vis[j] == 0) {q[tt++] = j;if (tt == N)tt = 0;vis[j] = 1;}}}}
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) {scanf("%d", &w[i]);}memset(hs, -1, sizeof hs);memset(ht, -1, sizeof ht);for (int i = 1,a,b,c; i <= m; i++) {scanf("%d%d%d", &a, &b,&c);add(hs, a, b), add(ht, b, a);if (c == 2) {add(hs, b, a), add(ht, a, b);}}spfa(hs, dmin, 0);spfa(ht, dmax, 1);int ret = 0;for (int i = 1; i <= n; i++) {ret = max(dmax[i] - dmin[i], ret);}cout << ret << endl;return 0;
}相关文章:
)
341. 最优贸易(dp思想运用,spfa,最短路)
341. 最优贸易 - AcWing题库 C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。 任意两个城市之间最多只有一条道路直接相连。 这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计…...
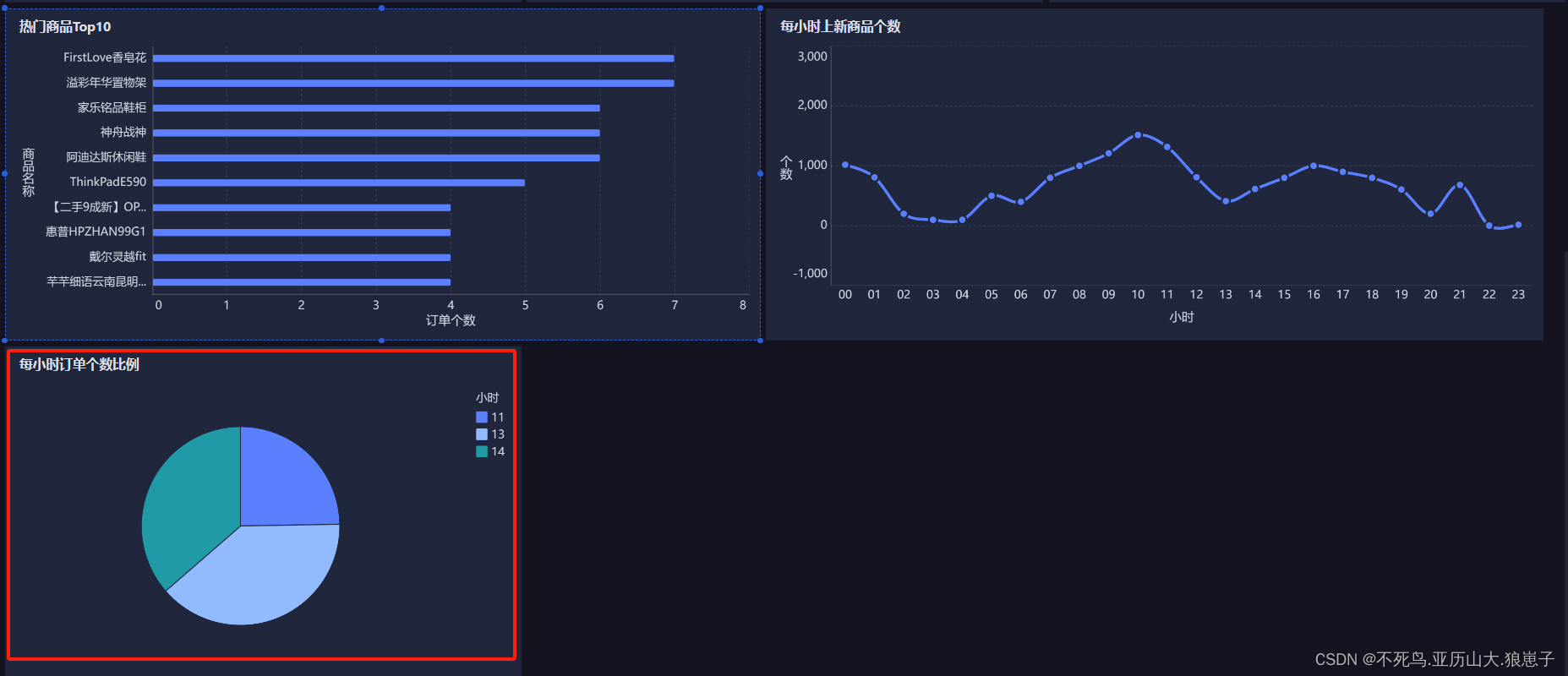
FineBI实战项目一(19):每小时订单笔数分析开发
点击新建组件,创建下每小时订单笔数组件。 选择饼图,拖拽cnt(总数)到角度,拖拽hourstr到颜色,调节内径。 修改现在的文字 拖拽组件到仪表盘。 效果如下:...

What is `@RequestBody ` does?
RequestBody 是SpringMVC框架中的注解,通常与POST、PUT等方法配合使用。当客户端发送包含JSON或XML格式数据的请求时,可以通过该注解将请求体内容绑定到Controller方法参数上 作用 自动反序列化: SpringMVC会根据RequestBody注解的参数类型&…...

Windows安装Rust环境(详细教程)
一、 安装mingw64(C语言环境) Rust默认使用的C语言依赖Visual Studio,但该工具占用空间大安装也较为麻烦,可以选用轻便的mingw64包。 1.1 安装地址 (1) 下载地址1-GitHub:Releases niXman/mingw-builds-binaries GitHub (2) 下载地址2-W…...

Marin说PCB之传输线损耗---趋肤效应和导体损耗01
大家在做RF上的PCB走线或者是车载相机的上走线的时候经常会听那些硬件工程师们说你这个走线一定要保证50欧姆的阻抗匹配啊,还有就是记得加粗走做隔层参考。 有的公司的EE硬件同事会很贴心的把RF走线的注意事项给你备注在原理图上或者是layoutguide上,遇到…...

八:分布式锁
1、为什么要使用分布式锁 锁是多线程代码中的概念,只有多任务访问同一个互斥的共享资源时才需要锁。单机应用开发时一般使用synchronized或lock。多线程的运行都是在同一个JVM之下。应用是分布式集群,属于多JVM的工作环境,JVM之间已经无法通过…...
)
示例:php将文本内容写入一个文件(面向过程写法)
一、封装2个函数,读写文件 /*** desc 读取文件内容* param string $filename* return array*/ private function readContent(string $filename): array {$text file_get_contents($filename);if (!$text) {return [];}$result json_decode($text,true);return…...

Flutter开发进阶之并发操作数据库
Flutter开发进阶之并发操作数据库 尽管 Flutter 本身不包含任何数据库功能,但可以使用各种第三方库和插件来在 Flutter 应用程序中实现数据库功能; 以下将使用sqflite作为例子,sqflite允许在 Flutter 应用程序中执行 SQL 查询,创…...
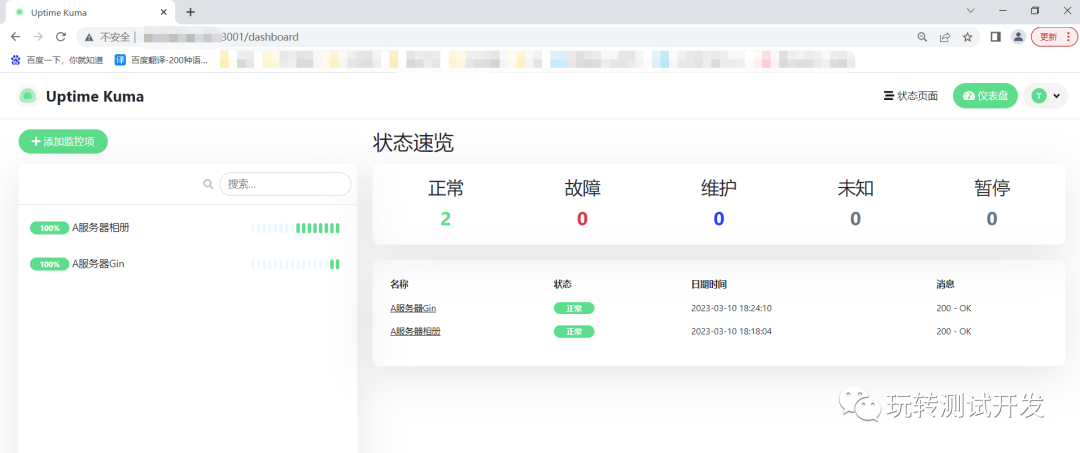
docker应用:搭建uptime-kuma监控站点
简介:Uptime Kuma是一个易于使用的自托管监控工具,它的界面干净简洁,部署和使用都非常方便。 历史攻略: docker:可视化工具portainer docker-compose:搭建自动化运维平台Spug 开源地址: ht…...

在illustrator中按大小尺寸选择物体 <脚本 018>
在Illustrator中我们可以依据对象的属性 如:填充颜色、描边颜色或描边宽度来选择相同属性的对象,但是Illustrator中没有根据不同大小尺寸来选择对象的功能,下面介绍的就是根据大小尺寸选择对象的脚本。 1、下面是当前画板中的所有对象&#…...

leetcode - 934. Shortest Bridge
Description You are given an n x n binary matrix grid where 1 represents land and 0 represents water. An island is a 4-directionally connected group of 1’s not connected to any other 1’s. There are exactly two islands in grid. You may change 0’s to 1…...
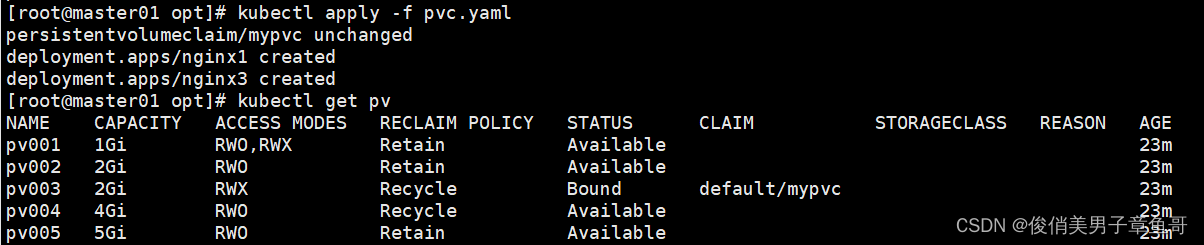
k8s的存储卷、数据卷
容器内的目录和宿主机目录进行挂载。 容器在系统上的生命周期是短暂的。 k8s用控制器创建的pod。delete相当于重启。容器的状态也会恢复到初始状态。一旦恢复到初始状态,所有的后天编辑的文件都会消失 容器和节点之间创建一个可以持久化保存容器内文件的存储卷。…...
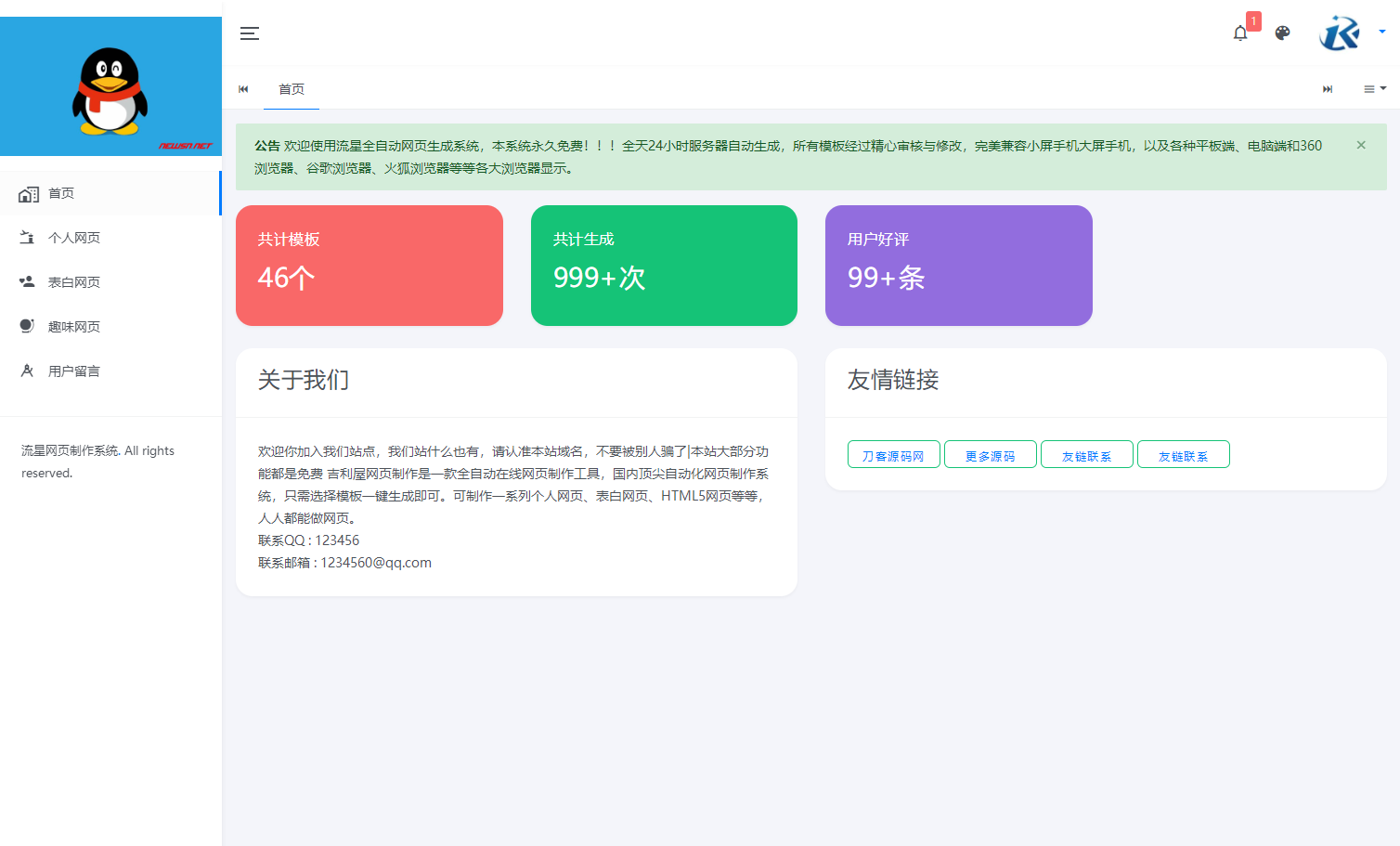
流星全自动网页生成系统重构版源码
流星全自动网页生成系统重构版源码分享,所有模板经过精心审核与修改,完美兼容小屏手机大屏手机,以及各种平板端、电脑端和360浏览器、谷歌浏览器、火狐浏览器等等各大浏览器显示。 为用户使用方便考虑,全自动网页制作系统无需繁琐…...
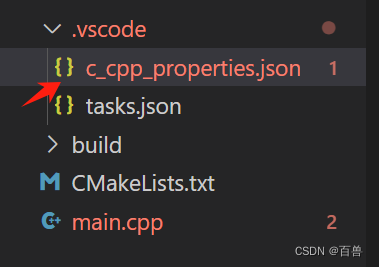
vscode打开c_cpp_properties.json文件的一种方式
步骤一 点击win32 步骤二 点击json 自动生成了...
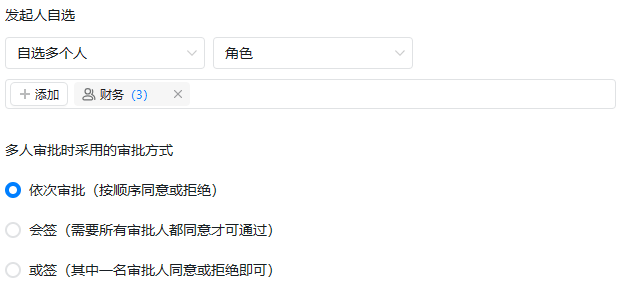
发起人自选-钉钉审批
场景描述 配置一个审批流程,在某些审批节点,不能确定谁具体来审批,所以需要手工选择一个人或者多个人保证流程能得以顺利通过。有些审批流程的做法是,上一个节点来选择指定的人,而钉钉的做法是发起人来指定。 钉钉设…...

电脑DIY-显卡
显卡 英伟达(NVIDIA)RTX系列 英伟达(NVIDIA) 英伟达(NVIDIA)是一家知名的图形处理器制造商,其显卡产品系列众多。以下是英伟达显卡的主要系列: 系列面向客户说明产品GeForce系列个…...
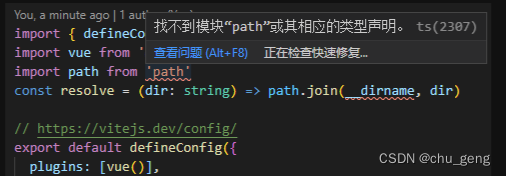
vue3+vite+ts+pinia新建项目(略详细版)
1、新建项目 npm create vite@latest 2、安装依赖 yarn add vue-router yarn add -D @types/node vite-plugin-pages sass sass-loader 3、配置别名 //vite.config.ts import { defineConfig } from vite import path from node:path export default defineConfig({ plu…...
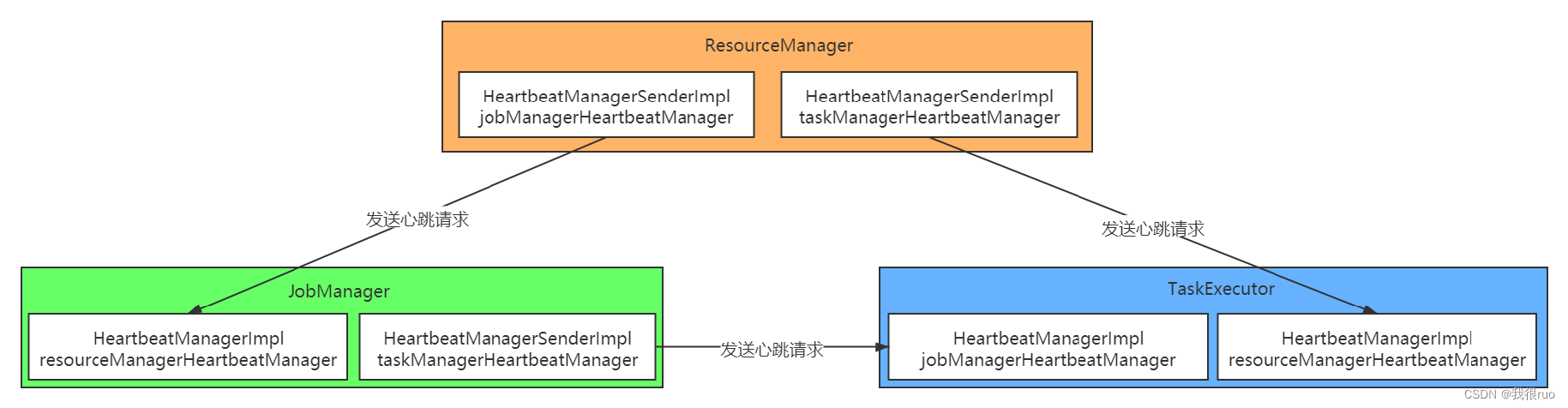
深入理解 Flink(五)Flink Standalone 集群启动源码剖析
前言 Flink 集群的逻辑概念: JobManager(StandaloneSessionClusterEntrypoint) TaskManager(TaskManagerRunner) Flink 集群的物理概念: ResourceManager(管理集群所有资源,管理集群所有从节点) TaskExecutor(管理从节点资源,接…...
SpringCloud Aliba-Nacos-从入门到学废【2】
🥚今日鸡汤🥚 比起不做而后悔,不如做了再后悔。 ——空白《游戏人生》 目录 🧈1.Nacos集群架构说明 🧂2.三种部署模式 🍿3.切换到mysql 1.在nacos-server-2.0.3\nacos\conf里找到nacos-mysql.sql 2.查…...

web前端算法简介之字典与哈希表
回顾 栈、队列 : 进、出 栈(Stack): 栈的操作主要包括: 队列(Queue): 队列的操作主要包括: 链表、数组 : 多个元素存储组成的 简述链表:数组&…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
