手撕乘积(**Multiplication** **Product**): 穷举和图示(2) 点积的几何意义
手撕乘积(Multiplication & Product): 穷举和图示(2) 点积的几何意义
点乘
x = 3
y = 5
xNda = np.arange(x)
>>> array([0, 1, 2])
x2Nda = xNda*2+1
>>> array([1, 3, 5])
yNda = np.arange(1, y)
>>> array([1, 2, 3, 4])
xyNda = np.meshgrid(xNda, yNda)
>>> array([[[0, 1, 2],[0, 1, 2],[0, 1, 2],[0, 1, 2]],[[0, 0, 0],[1, 1, 1],[2, 2, 2],[3, 3, 3]]])np.dot(x, y)
>>> 15
np.dot(xNda, x)
>>> array([0, 3, 6])
np.dot(xNda+3, xNda+7) # 👇图示之
>>> 98
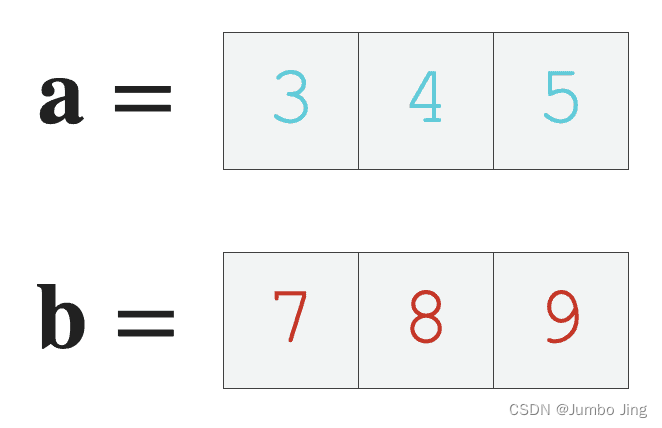
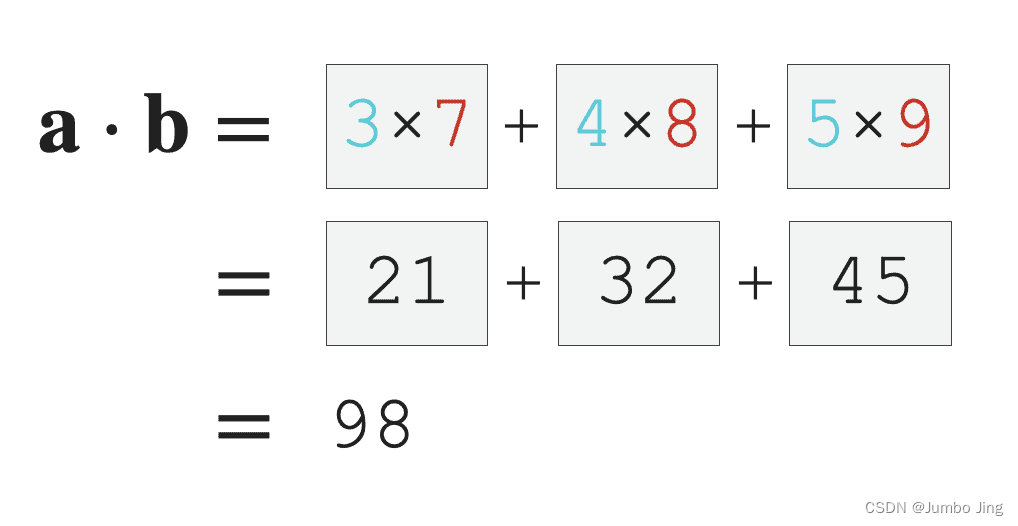
向量的点乘,也叫做向量的内积、数量积。对两个向量执行点乘运算,就是对着两个向量对应位置一一相乘之后求和的操作,点乘的结果是一个标量。
定义: 向量 a = [ a 1 , a 2 , . . . , a n ] a = [a_1, a_2, ..., a_n] a=[a1,a2,...,an] 和向量 b = [ b 1 , b 2 , . . . , b n ] b = [b_1, b_2, ..., b_n] b=[b1,b2,...,bn] 的内积为:
a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + . . . + a n b n a \cdot b = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + ... + a_n b_n a⋅b=∑i=1naibi=a1b1+a2b2+...+anbn
特别地, 0 ⋅ a = a ⋅ 0 = 0 0 \cdot a = a \cdot 0 = 0 0⋅a=a⋅0=0;若 a , b a, b a,b 是非零向量,则 a a a 与 b b b 正交的充要条件是 a ⋅ b = 0 a \cdot b = 0 a⋅b=0。
点积的几何意义: 可以用来表征或计算两个向量之间的夹角,以及在 b b b 向量在 a a a 向量方向上的投影,有公式:
a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ a \cdot b = |a| |b| \cos \theta a⋅b=∣a∣∣b∣cosθ
其中, θ \theta θ 为 a a a 与 b b b 之间的夹角。

根据这个公式就可以计算向量 a a a 和向量 b b b 之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
- a ⋅ b > 0 a \cdot b > 0 a⋅b>0,方向基本相同,夹角在 0 ° 0° 0° 到 90 ° 90° 90° 之间;
- a ⋅ b = 0 a \cdot b = 0 a⋅b=0,正交,相互垂直;
- a ⋅ b < 0 a \cdot b < 0 a⋅b<0,方向基本相反,夹角在 90 ° 90° 90° 到 180 ° 180° 180° 之间。
向量点乘的运算特性:
- a 2 ≥ 0 a^2 \geq 0 a2≥0;当 a 2 = 0 a^2 = 0 a2=0 时,必有 a = 0 a = 0 a=0; (正定性)
- a ⋅ b = b ⋅ a a \cdot b = b \cdot a a⋅b=b⋅a;(对称性)
- ( λ a + μ b ) ⋅ c = λ a ⋅ c + μ b ⋅ c (\lambda a + \mu b) \cdot c = \lambda a \cdot c + \mu b \cdot c (λa+μb)⋅c=λa⋅c+μb⋅c,对任意实数 λ , μ \lambda, \mu λ,μ 成立; (线性)
- cos ∠ ( a , b ) = a ⋅ b / ( ∣ a ∣ ∣ b ∣ ) \cos \angle (a, b) = a \cdot b / (|a| |b|) cos∠(a,b)=a⋅b/(∣a∣∣b∣);(余弦定理)
- ∣ a ⋅ b ∣ ≤ ∣ a ∣ ∣ b ∣ |a \cdot b| \leq |a| |b| ∣a⋅b∣≤∣a∣∣b∣,等号只在 a a a 与 b b b 共线时成立。
代码解释点积的几何意义:
问题:
向量 a = [ 1 , 0 ] a = [1, 0] a=[1,0]和 b = [ 1 , 2 ] b = [1, 2] b=[1,2]两个向量之间的夹角是多少?
用图解释一下:
import matplotlib.pyplot as plt
ndA = np.asanyarray
a = ndA((1,1))
b = ndA((3,2))
o = ndA((0,0))
abAngle = np.degrees(np.arccos(np.dot(a,b)/(np.linalg.norm(a)*np.linalg.norm(b))))
print(f'abAngle={abAngle}°')
plt.axis('equal')
plt.grid()
plt.plot(*zip(o,a), 'r')
plt.plot(*zip(o,b), 'b')
plt.show()
np.dot(xNda, xNda)
>>> 5
- 💡: 自己点乘自己相当于求向量的模的平方 a ⋅ a = ∣ a ∣ 2 a \cdot a = |a|^2 a⋅a=∣a∣2。
# 向量的模长(即到原点的距离)
np.linalg.norm(xNda)
xDst = np.dot(xNda, xNda)**.5
判断向量 a ⃗ \vec{a} a与 b ⃗ \vec{b} b是否正交, 是否同向…
def v1v2(a, b):dotAb = np.dot(a, b)if dotAb == 0:print('垂直')elif dotAb > 0:print('同向')elif dotAb < 0:print('反向')if abs(dotAb) == 1:print('平行')标量投影
a b = ∣ a ∣ cos θ a_b = |a| \cos \theta ab=∣a∣cosθ
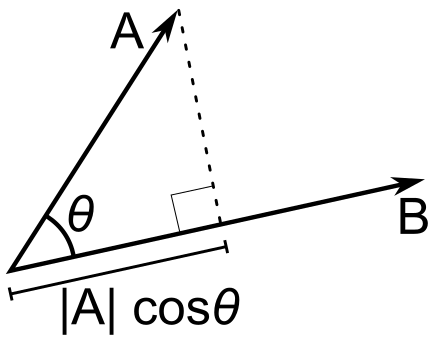
a b = ∣ a ∣ cos θ = a ⋅ b ∣ b ∣ = a ⋅ b ^ a_b = |a| \cos \theta = \frac{a \cdot b}{|b|} = a \cdot \hat{b} ab=∣a∣cosθ=∣b∣a⋅b=a⋅b^
# aPjb = lambda a, b: np.dot(a, b)/np.linalg.norm(b) * b/np.linalg.norm(b) # 向量a在向量b上的投影的标量(长度); 乘以向量b的单位向量, 得到向量a在向量b上的投影向量aPjb = lambda a, b: b * np.dot(a, b)/np.dot(b, b) # 获取向量a在向量b上的投影点()# 进一步简化, 已知b的单位向量
aPjbN = lambda a, bN: bN * np.dot(a, bN) # 获取向量a在向量b上的投影点()
- 注意⚠️: 👆🏻 a ⃗ \vec{a} a和 b ⃗ \vec{b} b的关系建立在笛卡尔坐标系, 原点o是起点.
引入第3点 c ⃗ \vec{c} c作为起点, 点>>线>>面, 让我们从起点o进入欧氏几何…
a + b
>>> array([4, 5])
c = ndA((1,3))
b - a
>>> array([2, 1])
a - b
>>> array([-2, -1])

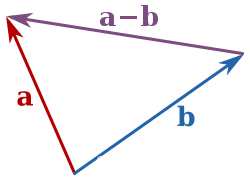
```pythonnp.linalg.norm(a-b) # 欧氏距离
>>> 2.23606797749979
∠ a b c \angle{abc} ∠abc = ?
abLen = lambda: a_b: np.linalg.norm(a_b)
acbAngle = np.degrees(np.arccos(np.dot(a-c, b-c)/(np.linalg.norm(a-c)*np.linalg.norm(b-c))))
print(f'acbAngle={acbAngle}°')
a到bc的距离:
a2bcLen = abLen(a - aPjb(c-a, b-c))升级继续, 让这些图形动起来:
点在空间中, 只有移动, 👇:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
o = ndA((0,0,0))
a = ndA((1,1,1))
b = ndA((3,2,1))
o + ndA((1, 0, 0)) # 表示o点在x轴上移动1个单位, y轴和z轴不变; 以此类推
def axMat(p, xyz='x', stp=1):if xyz == 'x':p1 = p + ndA((stp, 0, 0))elif xyz == 'y':p1 = p + ndA((0, stp, 0))elif xyz == 'z':p1 = p + ndA((0, 0, stp))return p1
# 同理, plnMat, 三维空间中的平面移动;
def plnMat(p, xyz='xy', stp=ndA((1,1))):if xyz == 'xy':p1 = p + ndA((stp[0], stp[1], 0))elif xyz == 'yz':p1 = p + ndA((0, stp[0], stp[1]))elif xyz == 'xz':p1 = p + ndA((stp[0], 0, stp[1]))return p1
# 如果都不为0, 就摆脱了轴和面的限制, 可以在空间中任意移动,,, 但是, 你得知道你要移动到哪里去...好无聊...我们先从二维的几何体开始
# 先建一个三角形abc
abcNda = ndA([[1,1], [3,2], [1,3]])
# tfMat = ndA([[r0c0, r0c1], [r1c0, r1c1]])
tfMat = lambda r0c0, r0c1, r1c0, r1c1: ndA([[r0c0, r0c1], [r1c0, r1c1]])所谓的变换矩阵(Transformation matrix), '就是一个二维数组, 用来描述一个几何体的变换, 例如: 旋转, 缩放, 平移等等…, ’ (👈🏻小c![]() 插话)是一个(n,n)的数组, 好吧…其实呢, 我们只需要知道:2x2, 3x3和4x4这三种矩阵来完成欧几里得变换, 先从二维开始…
插话)是一个(n,n)的数组, 好吧…其实呢, 我们只需要知道:2x2, 3x3和4x4这三种矩阵来完成欧几里得变换, 先从二维开始…
未完待续…
以上内容来自维基百科, 由![]() 协助完成.
协助完成.
相关文章:

手撕乘积(**Multiplication** **Product**): 穷举和图示(2) 点积的几何意义
手撕乘积(Multiplication & Product): 穷举和图示(2) 点积的几何意义 点乘 x 3 y 5 xNda np.arange(x) >>> array([0, 1, 2]) x2Nda xNda*21 >>> array([1, 3, 5]) yNda np.arange(1, y) >>> array([1, 2, 3, 4]) xyNda np.meshgrid(xN…...

postman环境变量全局变量设置
postman环境变量、全局变量设置 在公司中,一般会存在开发环境、测试环境、线上环境等,如果需要在不 同的环境下切换做接口测试,显然我们需要把所有接口的域名进行修改,如果接 口测试用例较多,那么修改会非常费力&…...

Linux 内核线程
文章目录 一、内核线程二、内核线程与普通进程的异同三、内核线程创建3.1 kernel_thread3.2 kthread_create 四、内核线程的退出四、示例代码参考资料 一、内核线程 内核线程就是内核的分身,一个分身可以处理一件特定事情。Linux内核使用内核线程来将内核分成几个功…...

Golang学习之路一七fmt的使用
Golang学习之路一七fmt的使用 格式化参数列表 格式含义%%一个%字面量%b一个二进制整数值(基数为 2),或者是一个(高级的)用科学计数法表示的指数为 2 的浮点数%c字符型。可以把输入的数字按照 ASCII 码相应转换为对应的字符%d一个十进制数值(基数为 10)%e以科学记数…...
windows使用redis-安装和配置
windows使用redis 安装和配置 下载安装方式一-使用压缩包安装解压到指定的文件Redis安装为Windows服务安装成功 方式二-MSI安装包安装完成 Redis配置远程访问1.修改配置文件redis.windows.conf2.修改完redis配置文件,必须重启redis 下载 先下载Redis for windows 的…...
)
Kafka系列(一)
内容 该系列主要是复习期间,通过浏览资料记录的一些笔记和重点,用于日常学习和学习后的总结。 组件概念 broker 一个Kafka的集群通常由多个broker组成,这样才能实现负载均衡、以及容错 broker是无状态(Sateless)的…...

Kotlin中的委托
在Kotlin中,委托是一种强大的设计模式,它允许一个类将其一些职责委托给另一个类。这种机制通过关键字by来实现。委托有助于代码的重用,降低耦合性,并提供更清晰的类设计。在Kotlin中,有两种主要类型的委托:…...
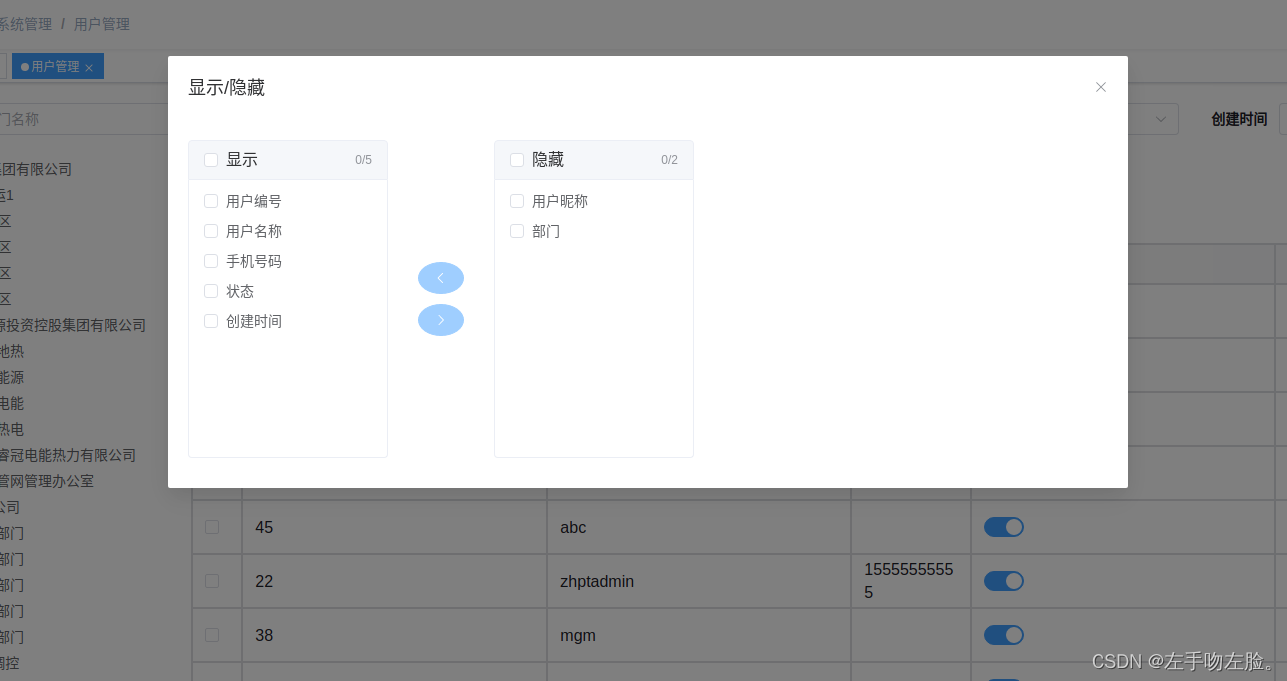
VUE2/3:element ui table表格的显隐列(若依框架)
若依框架自带一个组件,封装了关于表格,展示和隐藏表格列的功能; 使用效果就是这样的,在表格上面,三个框,从左到右分别是隐藏上面搜索,刷新列表,和显隐列的功能; 一、下面…...
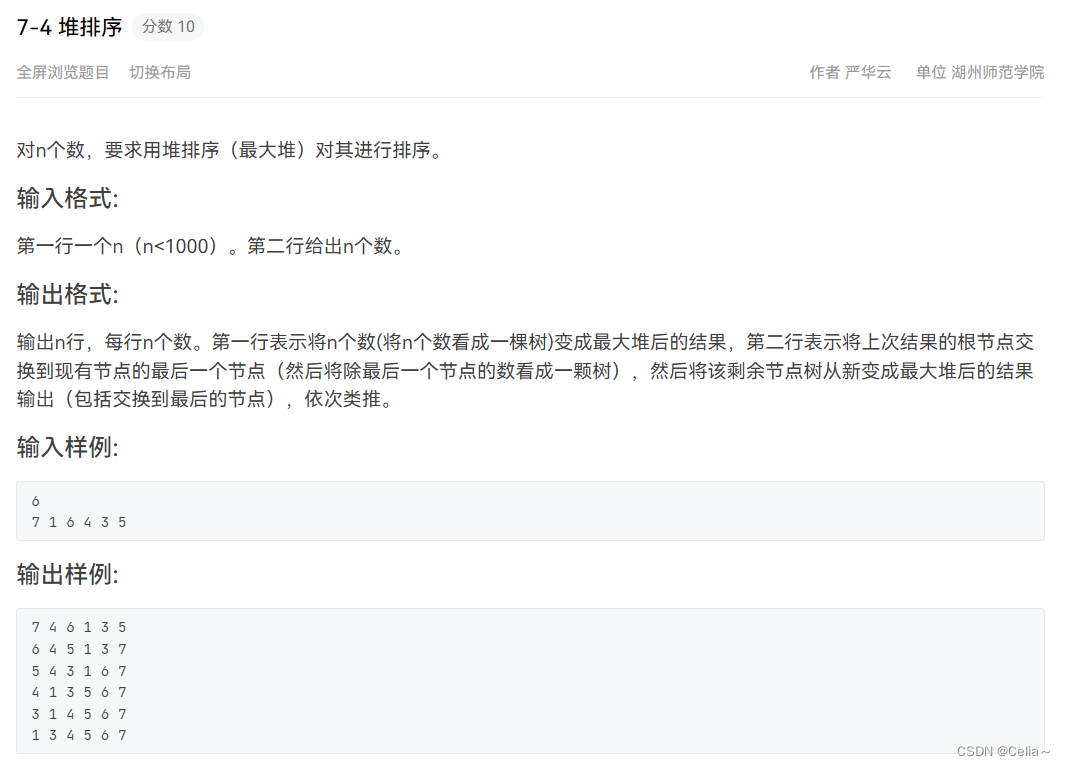
PTA-7-4 堆排序
代码如下: #include<iostream> using namespace std; void change(int arr[], int n, int i); int main() {int n,i,end,arr[1000];cin >> n;for (i 0; i < n; i){cin >> arr[i];}//进行一次排序,把最大值放到顶端for (i n/2-1; i > 0; i--){change…...
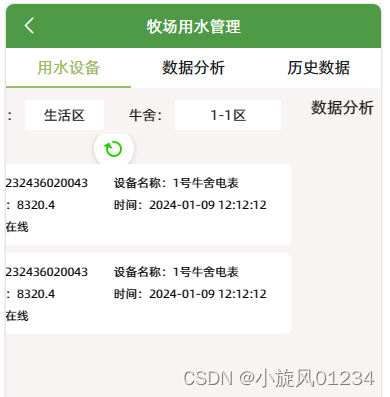
uniapp滑动页面切换和下拉刷新,触底加载更多(swiper + scroll-view)
因为官方文档乱七八糟的,所以自己来总结下 需求: 常见的上方tag标签切换,下方是页面,上面点击切换,下面页面也切换,下方列表有下拉刷新,触底加载更多 因为这两个组件都是固定高度的,…...
git 删除 submodule 子模块的步骤
实验有效,这里删除了两个 submodule。 1, 执行删除 submodule mkdir tmp1 && cd tmp1 && git clone --recursive ssh://gitaaa.bbb.ccc.git \ && cd ixsolver && git checkout -b abranch_01 \ && git submodule deini…...

一文彻底解析 Compose 的穿透刺客 -- CompositionLocal
Compose 官方说明一直很简洁:CompositionLocal 是通过组合隐式向下传递数据的工具。 两个核心:隐式、向下传递,咋一看很懵,先不着急去理解,我们先看一段非常简单的代码: class MainActivity : ComponentAc…...
)
iOS 位移枚举NS_OPTIONS(如何实现多个枚举值的同时传入判断)
一、场景 当我们使用枚举这个东西时,有时需要多个枚举值任一一个满足时就ture,但是常用的枚举NS_ENUM定义好的枚举只能挨个判断,写一坨就既不美观也不好阅读,如下: typedef NS_ENUM (NSInteger, RPTestType){RPTestT…...
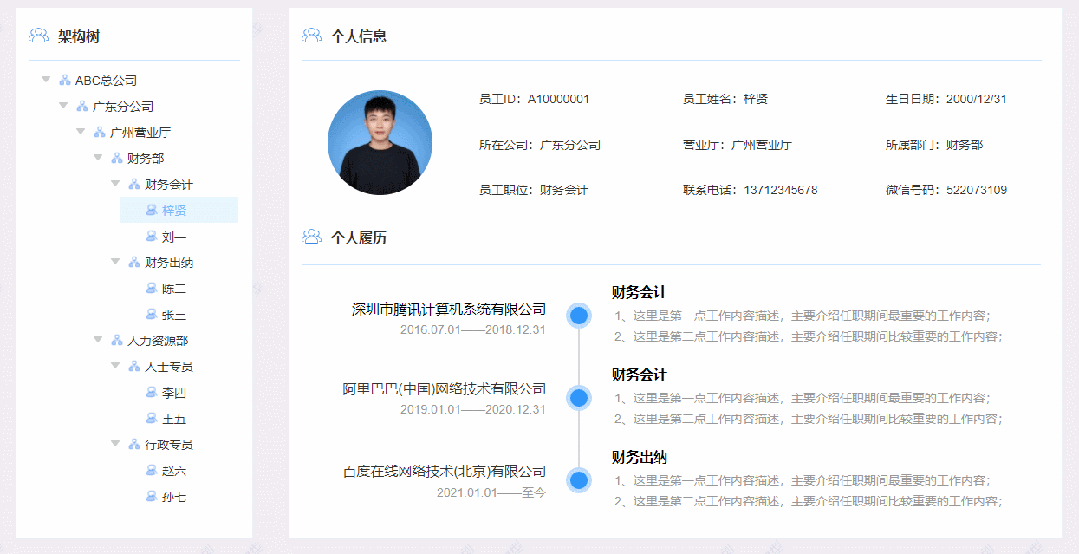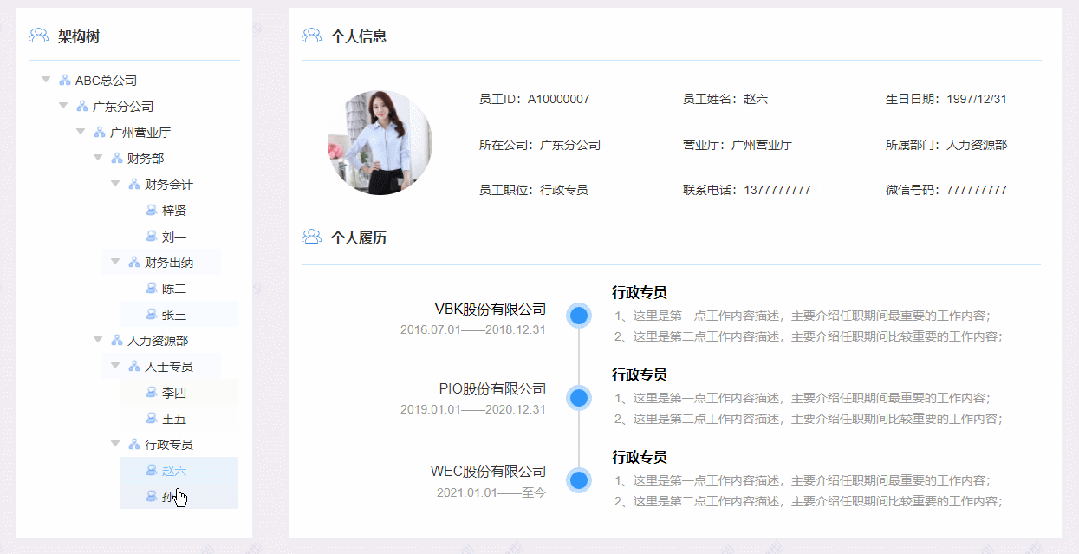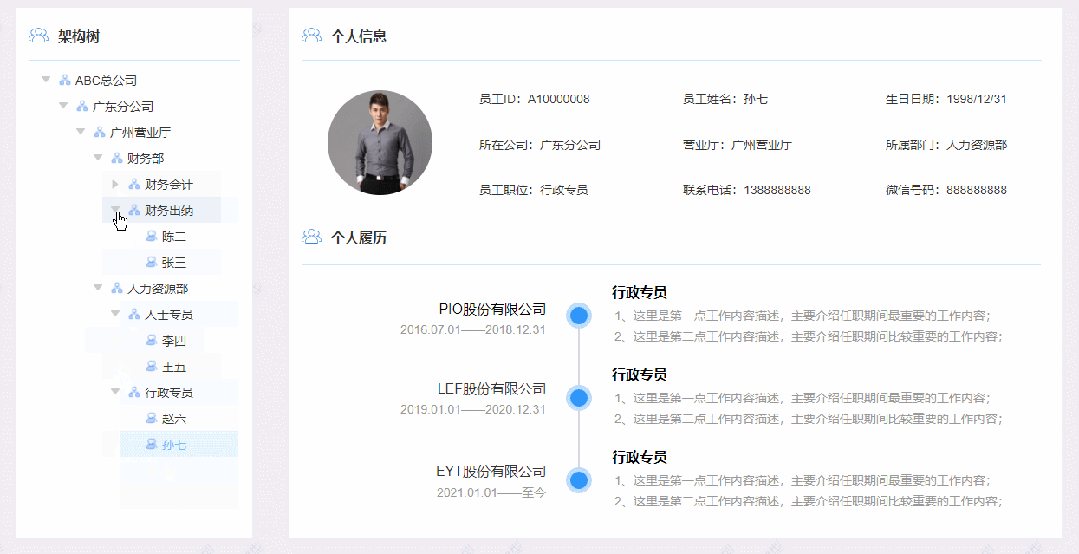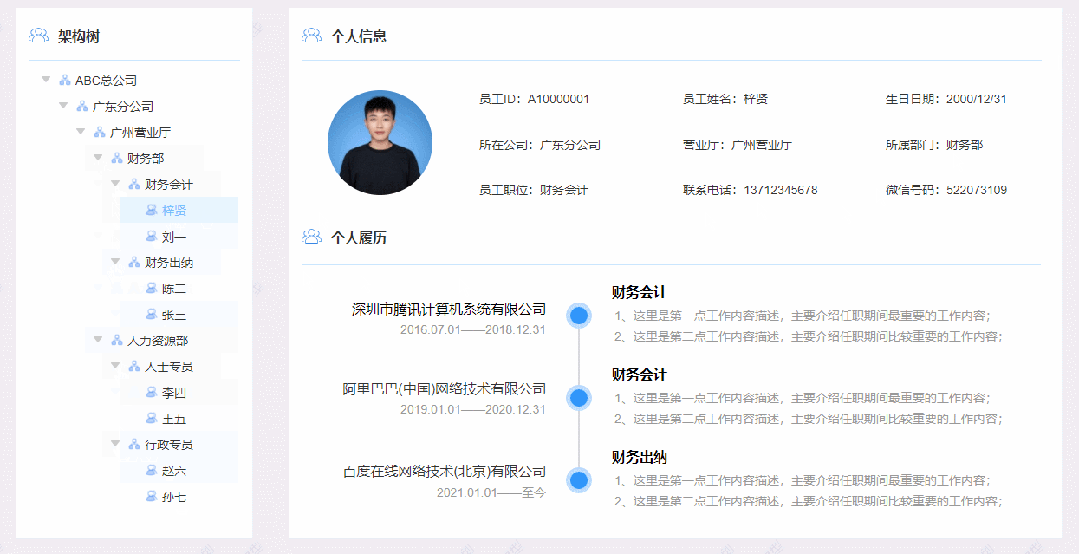
【Axure高保真原型】树控制内联框架
今天和大家分享树控制内联框架的原型模板,点击树的箭头可以打开或者收起子节点,点击最后一级人物节点,可以切换右侧内联框到对应的页面,左侧的树是通过中继器制作的,使用简单,只需要按要求填写中继器表格即…...

Visual Studio常用快捷键及调试操作
CtrlF10 运行到光标处 调试时候不用一行行按F10了CtrlMM 折叠或展开当前方法CtrlMO 折叠所有方法CtrlML 展开所有方法CtrlEW 自动换行/取消自动换行CtrlU 选中文本转小写CtrlShiftU 选中文本转大写CtrlWinO 启动软键盘F9 光标行加断点CtrlAltB 打开断点窗口 或通过Debug -> …...
MySQL 从零开始:02 MySQL 安装
文章目录 1、下载 MySQL 安装程序2、安装 MySQL 要操作 MySQL ,首先要安装 MySQL ,本文将一步步展示如何安装 MySQL,简直详细到令人发指。 环境: 操作系统:Windows10 64位MySQL版本:社区版 8.0.11.0 1、下…...
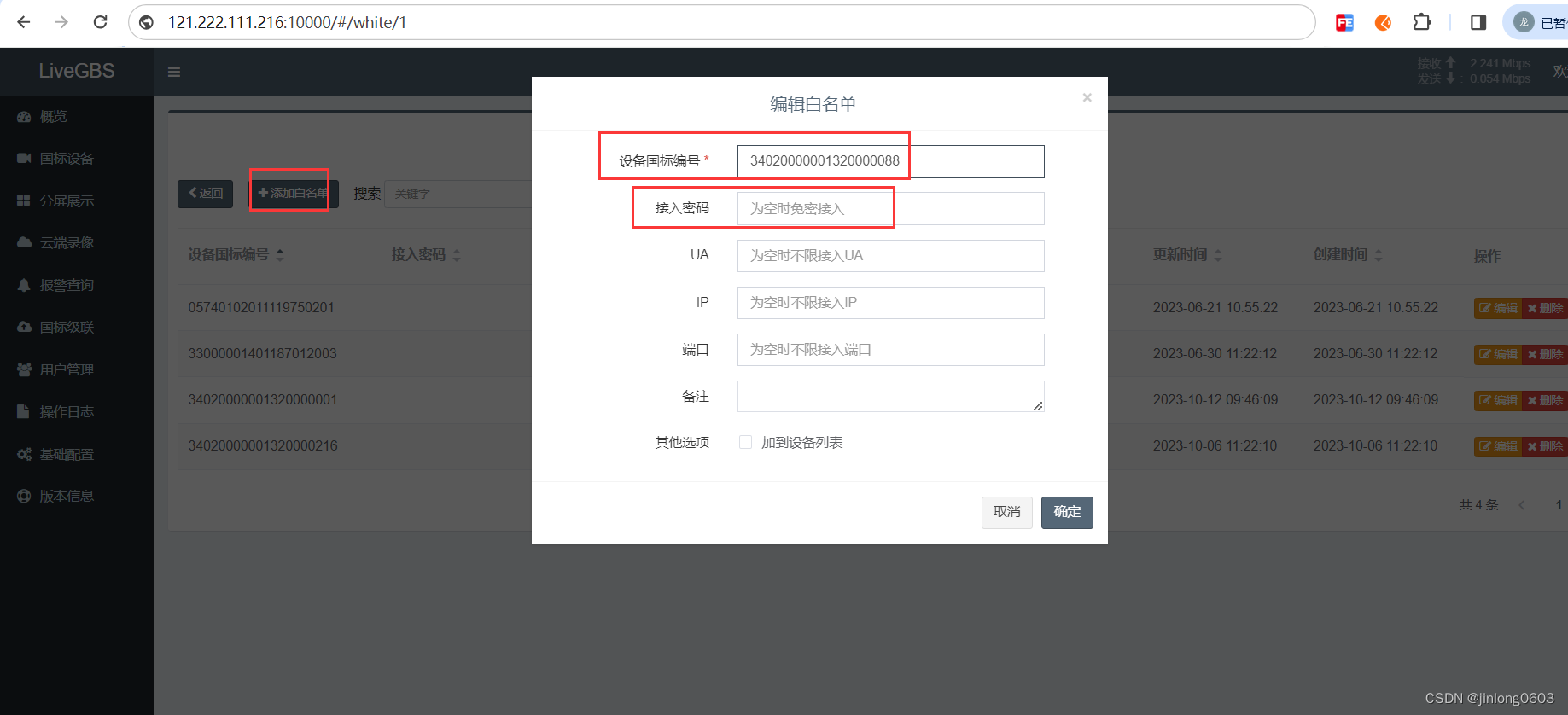
GB28181/GB35114平台LiveGBS何如添加白名单,使指定海康、大华、华为等GB28181摄像头或录像机设备可以免密接入
1、什么是GB/T28181级联 协议定义中的解释如下: 级联 cascadednetworking 两个信令安全路由网关之间按照上下级关系连接,上级中心信令控制服务器通过信令安全路由网 关可调用下级中心信令控制服务器所管辖的监控资源,下级中心信令控制服务器通过信令安全路由网 关向…...

【计算机组成与体系结构Ⅱ】MIPS指令系统(实验)
实验2:MIPS指令系统 一:实验目的 了解和熟悉指令级模拟器。熟练掌握MIPSsim模拟器的操作和使用方法。熟悉MIPS指令系统及其特点,加深对MIPS指令操作语义的理解。熟悉MIPS体系结构。 二:实验要求 采用指令集和流水线操作级模拟器…...

jsonvue-mobile 联动方式说明。
目录 jsonvue-mobile的联动类型分为两种 一种是命令式的: 另一种是响应式的: 联动场景 场景一:某一个字段的值变化时,同步修改另一个字段的值 命令式: 响应式: 场景一演示效果GIF 场景二ÿ…...

abseil中的微操
给分支预测器的建议 原始代码 以下代码用于实现多线程中只调用一次的效果,这里的if大多数情况下都是false,即已经被调用过了。这里是否被调用过用的是一个std::atomic<uint32_t>的原子变量 template <typename Callable, typename... Args>…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
