浮点数详解
目录
1.概述
2.浮点数的编码方式
2.1.float类型的IEEE编码
2.2.double类型的IEEE编码
2.3.现场问题
2.4.总结
1.概述
计算机也需要运算和存储数学中的实数。在计算机的发展过程中,曾产生过多种存储实数的方式,有的现在已经很少使用了。不管如何存储,都可以将其划分为定点实数存储方式和浮点实数存储方式两种。所谓定点实数,就是约定整数位和小数位的长度,比如用4字节存储实数,我们可以约定两个高字节存放整数部分,两个低字节存储小数部分。这样做的好处是计算效率高,缺点也显而易见:存储不灵活,比如我们想存储65536.5,由于整数的表达范围超过了2字节,就无法用定点实数存储方式了。对应地,也有浮点实数存储方式,道理很简单,就是用一部分二进制位存放小数点的位置信息,我们可以称之为“指数域”,其他的数据位用来存储没有小数点时的数据和符号,我们可以称之为"数据域" "符号域"。在访问时取得指数域,与数据域运算后得到真值,如67.625,利用浮点实数存储方式,数据域可以记录为67625,小数点的位置可以记为10的-3次方,对该数进行访问时计算一下即可。浮点实数存储方式的优缺点和定点实数存储方式的正好相反。在80286之前,程序员常常为实数的计算伤脑筋,而后来出现的浮点协处理器,可以协助主处理器分担浮点运算程序员计算实数的效率因此得到提升,于是浮点实数存储方式也就普及开来,成为现在主流的实数存储方式。但是,在一些条件恶劣的嵌入式开发场合,仍可看到定点实数的存储和使用。
在 C/C++中,使用浮点方式存储实数,用两种数据类型来保存浮点数: foat(单精度)和double(双精度)。float在内存中占4字节,double在内存中占8字节。由于占用空间大,double可描述的精度更高。这两种数据类型在内存中同样以十六进制方式存铺,但写大类型有所不同。
整型类型是将十进制转换成二进制保存在内存中,以十六进制方式显示。浮点类型并不是将一个浮点小数直接转换成二进制数保存,而是将浮点小数转换成的二进制码重新编码,再进行存储。C/C++的浮点数是有符号的。
在C/C++中,将浮点数强制转换为整数时,不会采用数学上四舍五人的方式,而是食弃掉小数部分,不会进位。
浮点数的操作不会用到通用寄存器,而是会使用浮点协处理器的浮点寄存器,专门对浮点数进行运算处理。
2.浮点数的编码方式
浮点数编码转换采用的是IEEE 规定的编码标准,float 和 double 这两种类型数据的转换原理相同,但由于表示的范围不一样,编码方式有些许区别。IEEE规定的浮点数编码会将一个浮点数转换为二进制数。以科学记数法划分,将浮点数拆分为3部分:符号、指数、尾数。
2.1.float类型的IEEE编码
foat类型在内存中占4字节(32位)。最高位用于表示符号,在剩余的31位中,从左向右取8位表示指数,其余表示尾数,如下图所示。

在进行二进制转换前,需要对单精度浮点数进行科学记数法转换。例如,将foat类型的12.25f转换为IEEE编码,须将12.25f转换成对应的二进制数1100.01,浮点数转二进制的方法为:二进制表示整数时,最低位代表2的0次方,往高位依次是2的1次方,2次方,3次方……那么对应的,二进制数小数点后面,最高位则是2的-1次方,-2次方,-3次方……如下图所示:

举几个例子:

那么12.25f转换成对应的二进制数的整数部分为1100,小数部分为01;小数点向左移动,每移动1次,指数加1,移动到除符号位的最高位为1处,停止移动,这里移动3次。对12.25f进行科学记数法转换后二进制部分为1.10001,指数部分为 3。在IEEE 编码中,由于在二进制情况下,最高位始终为1,为一个恒定值,故将其忽略不计。这里是一个正数,所以符号位添加0。
12.25f经 IEEE 转换后各位如下。
1)符号位:0
2)指数位:十进制 3+127=130,转换为二进制为10000010。
3)尾数位:10001000000000000000000(当不足23位时,低位补0填)。
由于尾数位中最高位1是固定值,故忽略不计,只要在转换回十进制数时加1即可。为什么指数位要加 127呢?这是因为指数可能出现负数,十进制数 127 可表示为二进制数01111111,IEEE编码方式规定,当指数小于0111111时为一个负数,反之为正数,因01111111为0。
将示例中转换后的符号位、指数位和尾数位按二进制拼接在一起,就成为一个完整的IEEE 浮点编码:01000001010001000000000000000000。转换成十六进制数为0x41440000内存中以小端方式进行排列,故为 00004441,分析结果如下图所示。 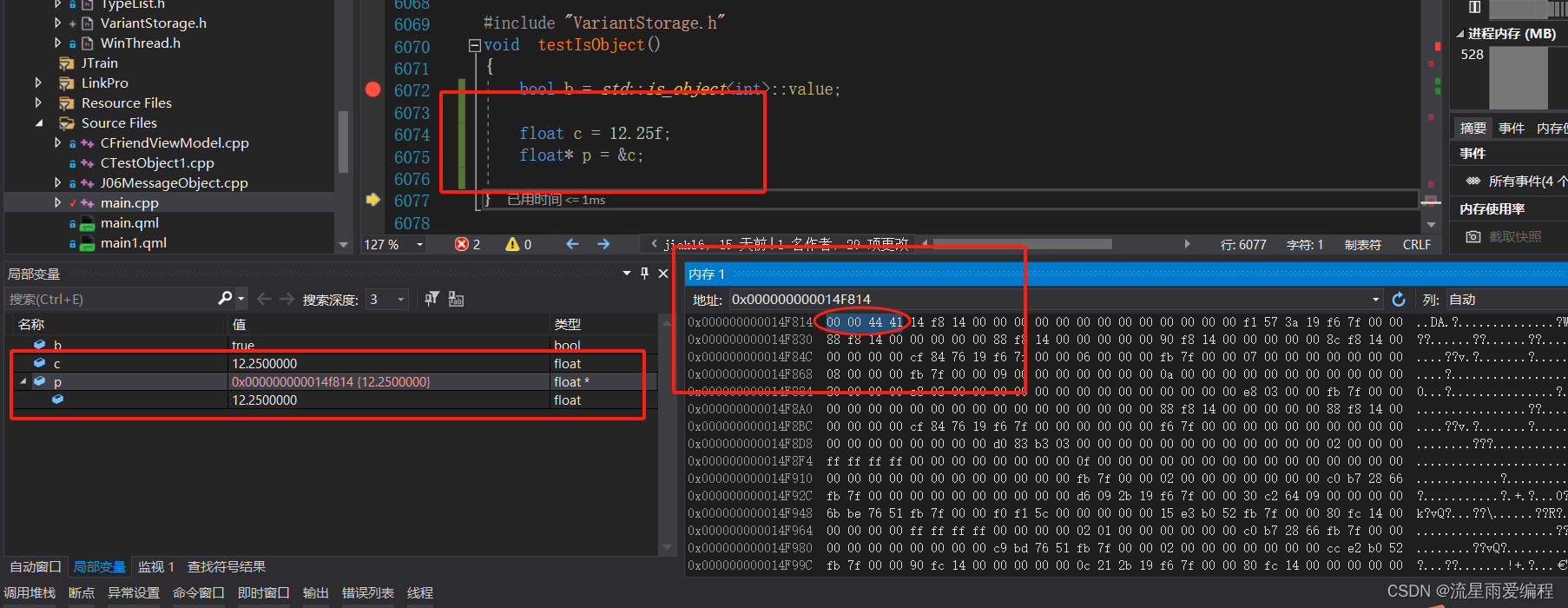
使用第三方工具软件计算更清楚更简便,如下图所示:
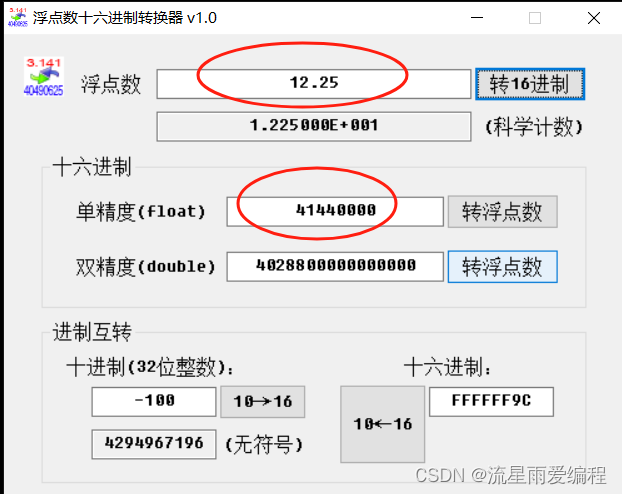
上面演示了符号位为正、指数位也为正的情况。那么什么情况下指数位可以为负呢?根据科学记数法,小数点向整数部分移动时,指数做加法。相反,小数点向小数部分移动时,指数需要以0起始做减法。浮点数-0.125f转换EEE编码后,将会是一个符号位为1、指数部分为负的数。-0.125f经转换后二进制部分为0.001,用科学记数法表示为1.0,指数为 -3。
-0.125fIEEE 转换后各位的情况如下。
1)符号位:1。
2)指数位:十进制 127+(-3 ),转换为二进制是 01111100,如果不足8位,则高位补 0。
3)尾数位:00000000000000000000000。
-0.125f转换后的 IEEE 编码二进制拼接为 10111110000000000000000000000000。转换成十六进制数为 0xBE000000,内存中显示为00 00 00 BE,分析结果如下图所示。
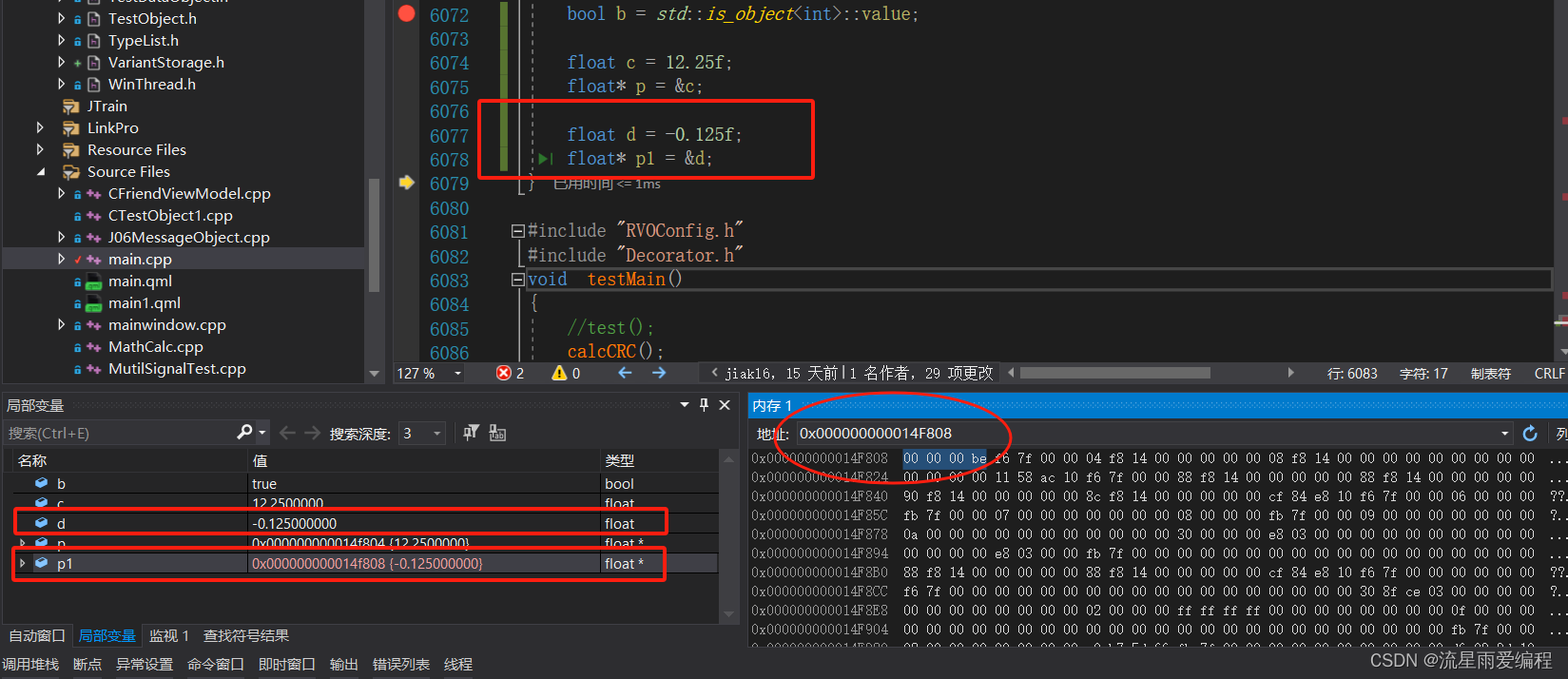
使用第三方工具软件计算更清楚,如下图所示:
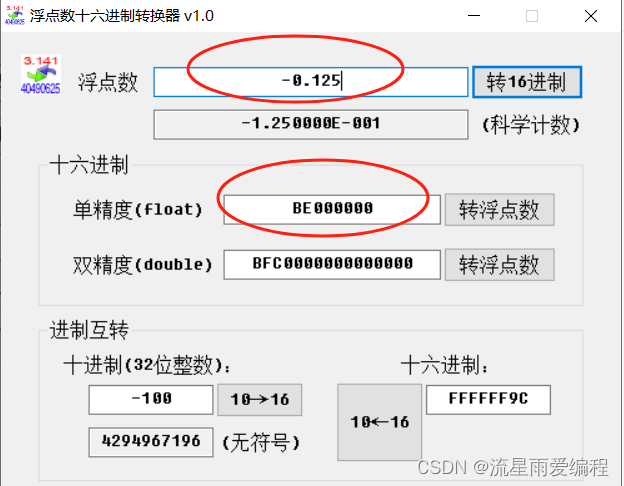
上面的两个浮点数小数部分转换为二进制时都是有穷的,如果小数部分转换为二进时得到一个无穷值,则会根据尾数部分的长度舍弃多余的部分。如单精度浮点数1.3f,数部分转换为二进制就会产生无穷值,依次转换为0.3、0.6、1.2、0.4、0.8、1.6、1.2、00.8……转换后得到的二进制数为 1.01001100110011001100110,到第23 位终止,尾数部分无法保存更大的值。
1.3f经 EEE 转换后各位的情况如下:
1)符号位:0。
2)指数位:十进制 0+127,转换二进制01111111。
3)尾数位:01001100110011001100110。
1.3f转换后的IEEE编码二进制拼接为00111111101001100110011001100110。转换十六进制数为0x3FA66666,在内存中显示为66 66 A6 3F。由于在转换二进制过程中产些了无穷值,舍弃了部分位数,所以进行IEEE编码转换后得到的是一个近似值,存在一定的误差。再次将这个IEEE编码值转换成十进制小数,得到的值为12516582,四合五人保留位小数之后为1.3。这就解释了为什么C++在比较浮点数值是否为0时,要做一个区同中较而不是直接进行等值比较。正确浮点数比较如下代码:
float f1=0.0001f;
if(f2 >=-f1 6& f2 <= f1)
{// f1等于0
}2.2.double类型的IEEE编码
前文讲解了单精度浮点类型的IEEE编码。double类型和 foat类型大同小异,只是double类型表示的范围更大,占用空间更多,是 foat类型所占空间的两倍。当然,精准度double 类型占8字节的内存空间,同样,最高位也用于表示符号,指数位占11位,剩也会更高。
在 float类型中,指数位范围用8位表示,加127后用于判断指数符号。在double类型余 52 位表示位数。中,由于扩大了精度,因此指数范围使用11位正数表示,加1023 后可用于指数符号判断。double 类型的 IEEE 编码转换过程与 foat 类型一样,读者可根据 foat类型的转换流程来转换 double类型,此处不再赘述。
2.3.现场问题
通过上面的讲解,我们知道浮点数是有可能出现经过IEEE编码转换后得到的是一个近似值,跟实际值存在一定的偏差。项目前期制定的设备两端通信协议设计某些字段为double类型,导致采集数据设备采集到的两端的二进制数据不一致的问题。后期调整,全部把double类型的数据转换为整数进行传输,才保证了两端二进制数据的一致性。
2.4.总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注本博客的其它内容。
参考:
浮点数与十六进制转换工具下载地址:https://download.csdn.net/download/haokan123456789/88771127?spm=1001.2014.3001.5501 浮点类型(float、double)在内存中如何存储?-腾讯云开发者社区-腾讯云
C++:float型数据存储原理及精度丢失溢出深入解析 - 知乎
相关文章:

浮点数详解
目录 1.概述 2.浮点数的编码方式 2.1.float类型的IEEE编码 2.2.double类型的IEEE编码 2.3.现场问题 2.4.总结 1.概述 计算机也需要运算和存储数学中的实数。在计算机的发展过程中,曾产生过多种存储实数的方式,有的现在已经很少使用了。不管如何存储…...

LED流水灯
这段代码是用于STM32F10x系列微控制器的程序,主要目的是初始化GPIOA并使其所有引脚按照特定的模式进行闪烁。下面是对这段代码的逐行解释: #include "stm32f10x.h":这一行包含了STM32F10x系列微控制器的设备头文件。这个头文件包含…...
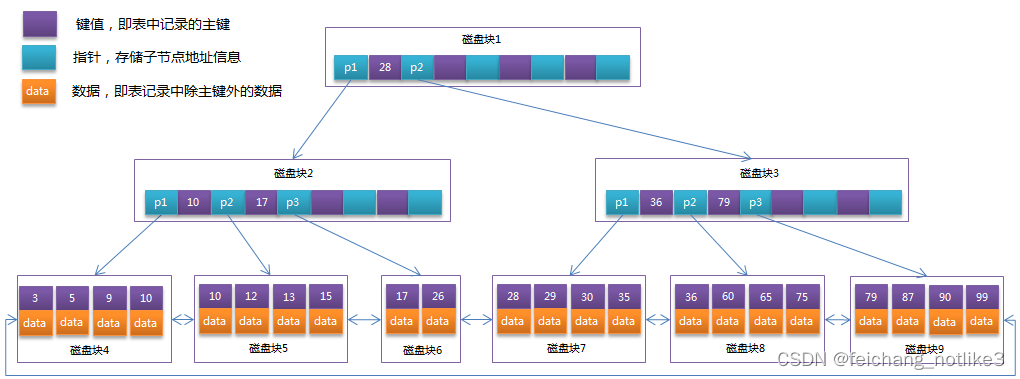
MySQL-B-tree和B+tree区别
B-tree(平衡树)和Btree(平衡树的一种变种)是两种常见的树状数据结构,用于构建索引以提高数据库的查询性能。它们在一些方面有相似之处,但也有一些关键的区别。以下是B-tree和Btree的主要区别: …...
架构篇08:架构设计三原则
文章目录 合适原则简单原则演化原则小结 成为架构师是每个程序员的梦想,但并不意味着把编程做好就能够自然而然地成为一个架构师,优秀程序员和架构师之间还有一个明显的鸿沟需要跨越,这个鸿沟就是“不确定性”。 对于编程来说,本…...
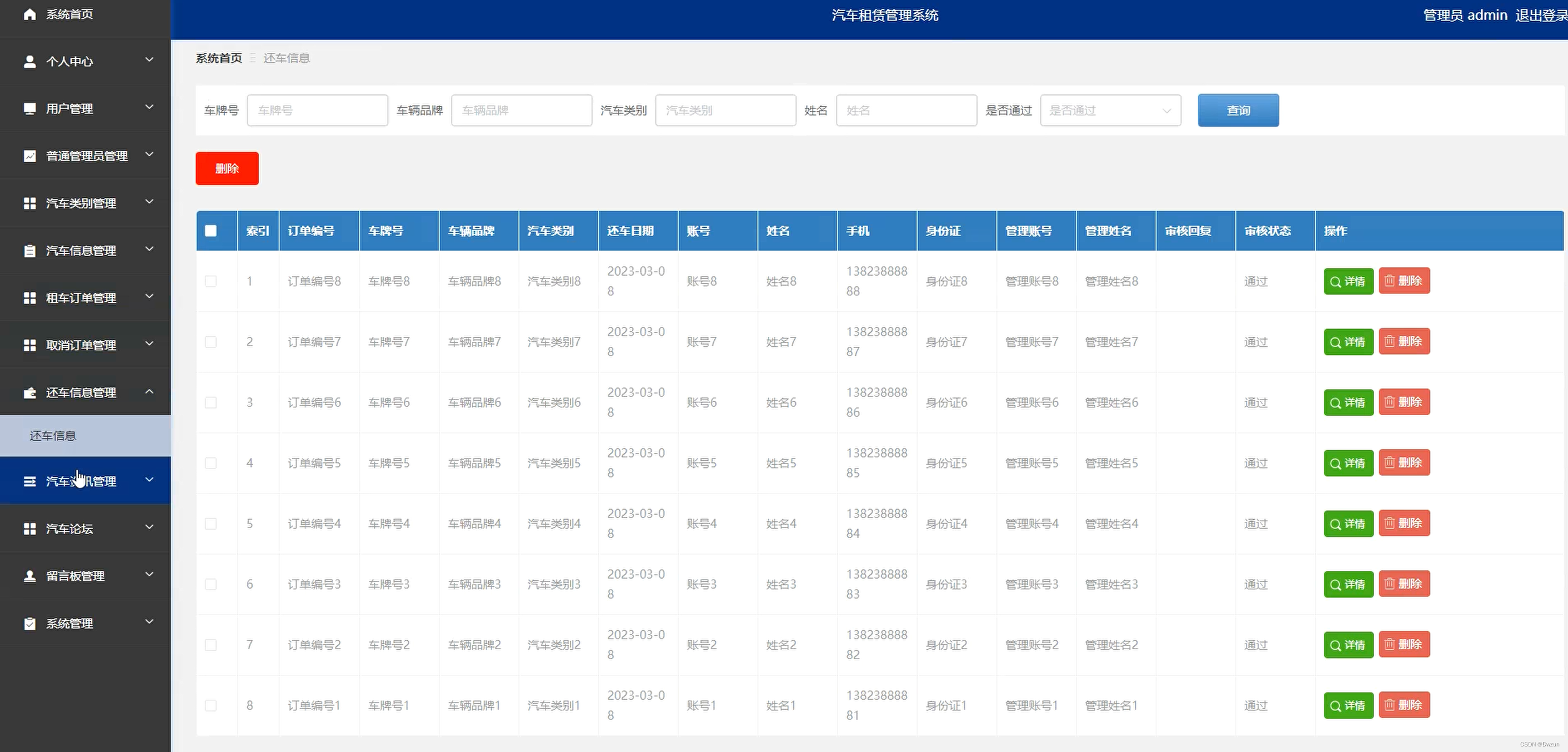
基于SpringBoot Vue汽车租赁系统
大家好✌!我是Dwzun。很高兴你能来阅读我,我会陆续更新Java后端、前端、数据库、项目案例等相关知识点总结,还为大家分享优质的实战项目,本人在Java项目开发领域有多年的经验,陆续会更新更多优质的Java实战项目&#x…...

idea带的maven在SpringBoot下载jar包出错、下载jar包速度慢
找到idea安装目录 /IntelliJ IDEA/plugins/maven/lib/maven3/conf/settings.xml 搜索:mirrors 添加到mirrors标签里。(默认下载包是从国外拉取,速度慢,现在替换成国内阿里的链接) <mirror><id>central</id><…...

datasets的一些使用技巧
#加载某类文件作为数据集 dataset load_dataset("json", data_files"./train_pair_1w.json", split"train") #加载数据集中的子数据集 datasets load_dataset("clue",name"afqmc",#trust_remote_codeTrue) train_datas…...
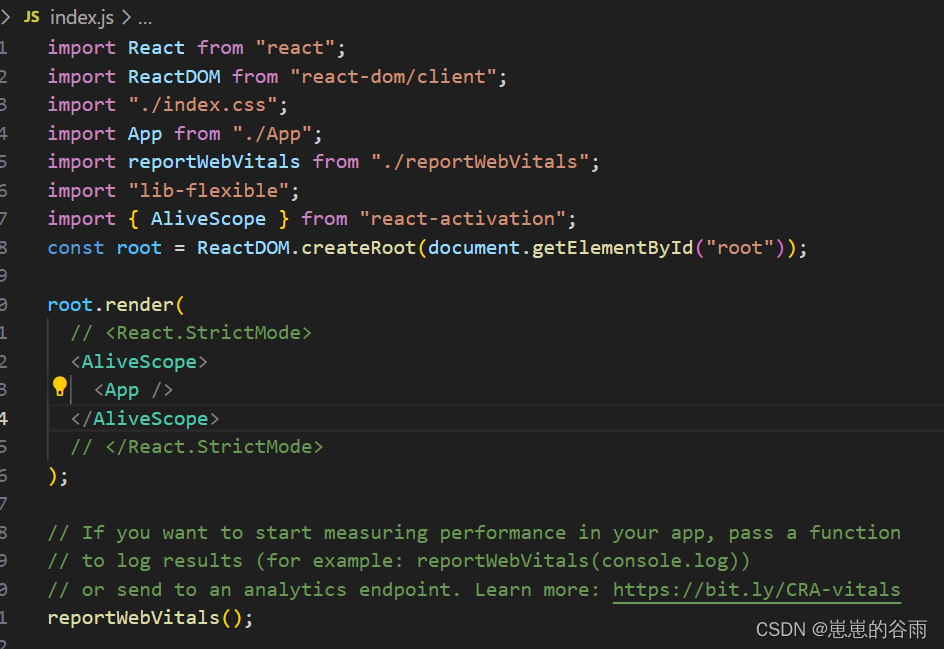
react 实现页面状态缓存(keep-alive)
前言: 因为 react、vue都是单页面应用,路由跳转时,就会销毁上一个页面的组件。但是有些项目不想被销毁,想保存状态。 比如:h5项目跳转其他页面返回时,页面状态不丢失。设想一个 页面我滑倒了中间…...

spring和springboot、springMVC有什么区别?
前言 大家好,我是chowley,今天来聊一下,刚在面试中被问到的一个经典问题 spring和springboot、springMVC有什么区别? Spring、Spring Boot 和 Spring MVC 是 Spring Framework 生态中的不同组件,各自有不同的角色和…...

centos 启动nacos pg版本
背景:支持国产化需求,不再使用mysql 1.修改插件 git clone https://github.com/wuchubuzai2018/nacos-datasource-extend-plugins.git cd nacos-datasource-extend-plugins/nacos-postgresql-datasource-plugin-ext mvn package编译成功后,…...

实验:MySQL 客户端SocketTimeout 抓包分析
实验准备 服务端环境准备 服务器信息 阿里云 99 大洋白嫖机 $ cat /proc/version Linux version 5.15.0-83-generic (builddlcy02-amd64-027) (gcc (Ubuntu 11.4.0-1ubuntu1~22.04) 11.4.0, GNU ld (GNU Binutils for Ubuntu) 2.38) #92-Ubuntu SMP Mon Aug 14 09:30:42 UT…...

rocketmq双主双从部署+dashbord
1、主机规划 主机节点地址主机Anamesrv192.168.2.228:9876主机Abroker-a192.168.2.228:10911主机Abroker-b192.168.2.228:11911主机Bnamesrv192.168.2.229:9876主机Bbroker-c192.168.2.229:10911主机Bbroker-d192.168.2.229:11911 2、两台主机都需要执行,创建mq需…...

OpenHarmony当前进展和未来趋势
操作系统自20世纪50年代诞生,经历了从专用操作系统到通用操作系统的转变。整体可以将操作系统的发展历史分为3个阶段:PC时代、移动互联网时代、万物互联时代。 PC时代主要以计算机为主,用户规模从1970年的10亿增长到1990年的30亿。这一时代诞…...

php学习
php基础语法 一 php程序 1.php标记 开始标记<?php 和结束标记 ?>中间写 PHP 代码 当解析一个文件时,PHP 会寻找起始和结束标记,也就是告诉php 开始和停止解析二者之间的代码。此种解析方式使得PHP 可以被嵌入到各种不同的文档中去ÿ…...

ruoyi框架教程
心血来潮,写一篇关于ruoyi【若依】框架从0-1的教程。说一下使用感受吧,如果有一个架构师或者老手已经把架构改造完成也能指导你如何快速上手,那么你在后面的增删改查系列开发起来会如鱼得水。如果没有人改造,也没有人教你…...

通过浏览器URL地址,5分钟内渗透你的网站!很刑很可拷!
今天我来带大家简单渗透一个小破站,通过这个案例,让你深入了解为什么很多公司都需要紧急修复各个中间件的漏洞以及进行URL解析拦截等重要操作。这些措施的目的是为了保护网站和系统的安全性。如果不及时升级和修复漏洞,你就等着被黑客攻击吧&…...
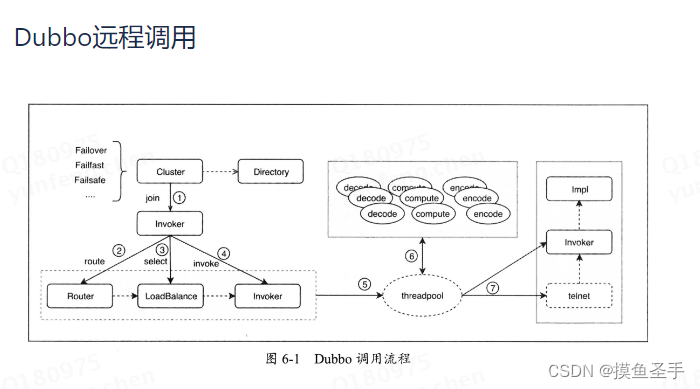
dubbo:深入理解Apache Dubbo与实战
dubbo核心组件 层次名 作 用 Service 业务层。包括业务代码的接口与实现,即开发者实现的业务代码 config 配置层。主要围绕ServiceConfig (暴露的服务配置)和ReferenceConfig (引用的服务配置)两个实现类展开…...
写着玩的程序:pycharm实现无限弹窗程序(非病毒程序,仅整蛊使用)
运行环境 PyCharm 2023.2.1 python3.11 具体内容 源代码 import tkinter as tk from tkinter import messagebox import threadingclass PopupGenerator:def __init__(self):self.root tk.Tk()self.root.geometry("200x120")self.root.title("无限弹窗&qu…...

计算机网络——运输层(2)暨小程送书
计算机网络——运输层(2)暨小程送书 小程一言专栏链接: [link](http://t.csdnimg.cn/ZUTXU) 运输层(2)TCP/IP对比TCP(传输控制协议):IP(互联网协议):总结 拥塞…...

FPGA高端项目:Xilinx Zynq7020 系列FPGA纯verilog图像缩放工程解决方案 提供3套工程源码和技术支持
目录 1、前言版本更新说明给读者的一封信FPGA就业高端项目培训计划免责声明 2、相关方案推荐我这里已有的FPGA图像缩放方案本方案在Xilinx Kintex7 系列FPGA上的应用本方案在Xilinx Artix7 系列FPGA上的应用本方案在国产FPGA紫光同创系列上的应用本方案在国产FPGA高云系列上的应…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
