GAMES104-现代游戏引擎:从入门到实践 - 物理引擎课程笔记汇总
文章目录
- 0 入门资料
- 1 物理引擎
- 基本概念
- Actor & shapes
- Rigid body dynamics
- Collision Detection
- Collision Resolution
- 应用与实践
- Character controller
- Ragdoll
0 入门资料
- GAMES104-现代游戏引擎:从入门到实践_课程视频_bilibili
- GAMES104官方账号 - 知乎
- 课程主页
- 课程小引擎Piccolo
- 课件:
- GAMES104_Lecture10_Physics System_Basic Concepts.pdf
- GAMES104_Lecture11_Physics System_Applications.pdf
1 物理引擎
- 物理引擎的用途:
- 碰撞检测
- 解决碰撞、其它约束限制
- 更新所有物体的世界坐标(world Transform)
基本概念
Actor & shapes
Actor
- 静态 static actor:不会移动,阻碍你
- 动态 dynamics actor:符合动力学原理,可以被 forces、torque、impulse影响
- 触发器 trigger
- kinematic actor:可以违背物理学,让它按照设计的运动
Actor Shapes
- 求交点
| Shapes | 图例 | 备注 |
|---|---|---|
| Spheres 球体 |  | |
| Capsules 胶囊体 | 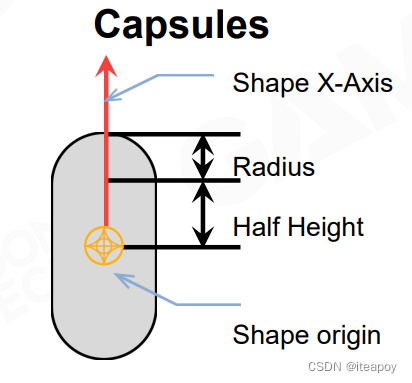 | - 人体 |
| Boxes 盒子 | 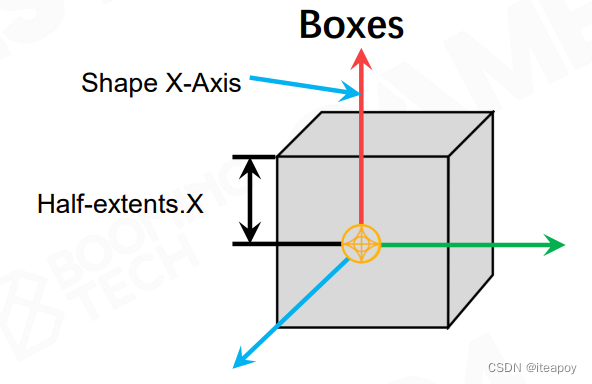 | |
| Triangle Meshes 三角 | 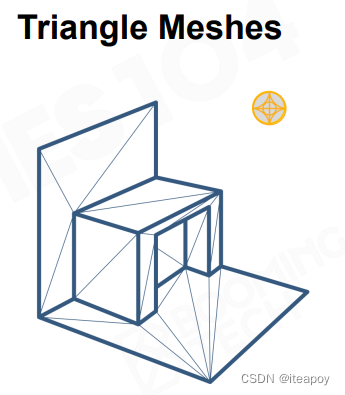 | - 必须是密闭的 - Dynamic actors 不能使用 |
| Height Fields | 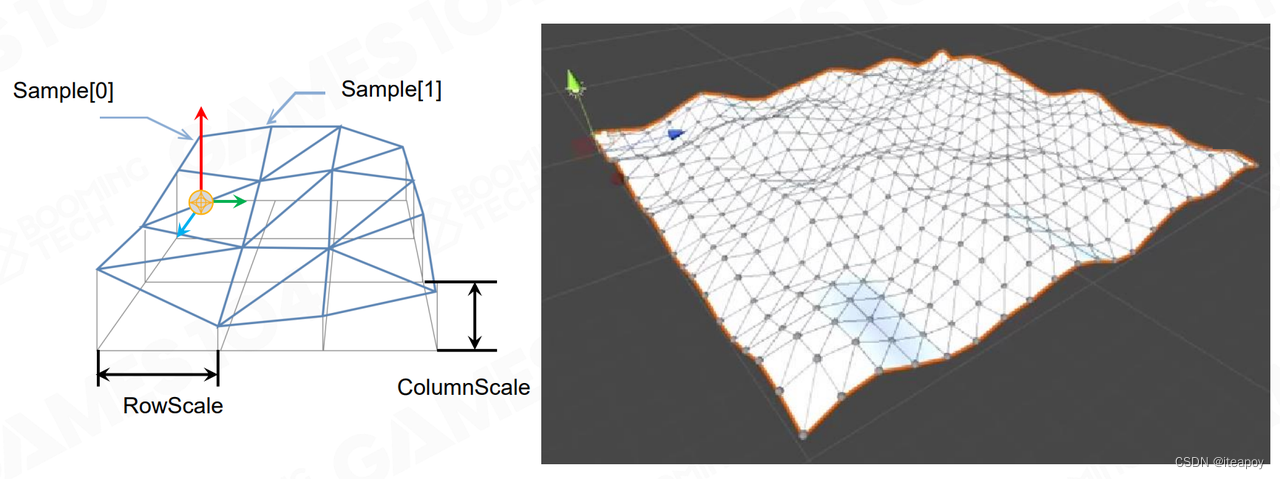 | - 用于地形 |
Shape 的属性
- 质量/密度 Mass and Density
- 质心 Center of Mass
- 摩擦力/弹性 Friction & Restitution :受到物理材质的影响
- 力 Forces:常见的力包括拉力、重力、摩擦力
- 冲力/冲量 impulse:例如爆炸
- 移动 movement
半隐式欧拉积分
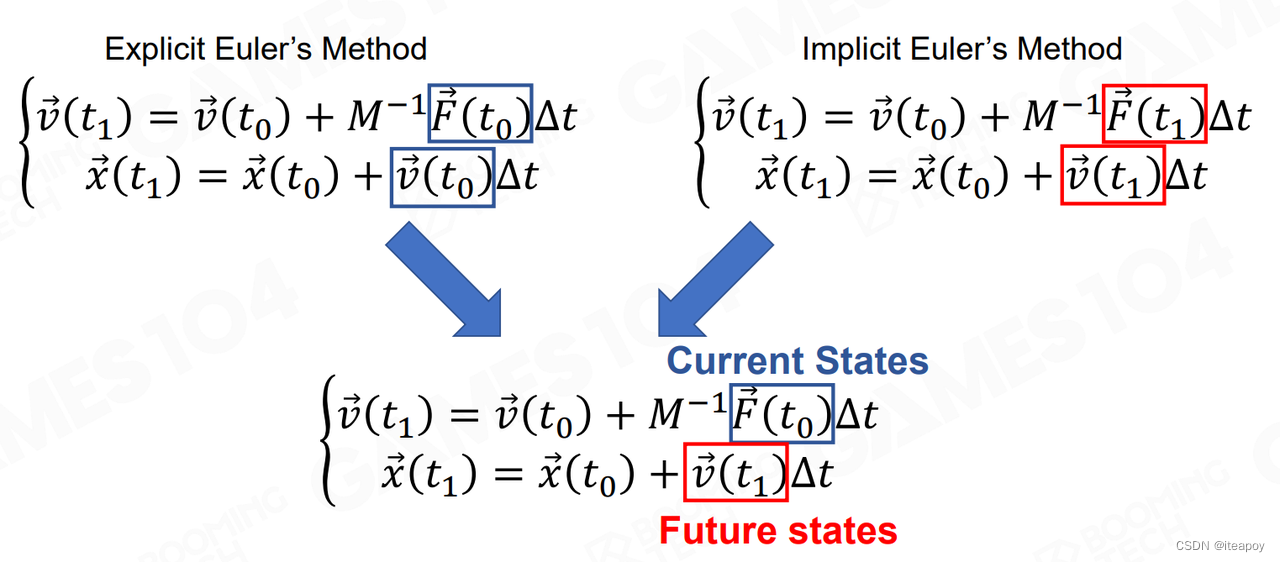
- 【优点】
- 容易模拟
- 较稳定
- 【缺点】
- 实际消耗时间比真实时间要久一点
Rigid body dynamics
| 粒子动力学 Particle Dynamics | 刚体动力学 Rigid body Dynamics |
|---|---|
| 位置 Position x ⃗ \vec{x} x | 旋转 Orientation R \boldsymbol{R} R |
| 线速度 Linear Velocity v ⃗ = d x ⃗ d t \vec{v}=\frac{\mathrm{d} \vec{x}}{\mathrm{~d} t} v= dtdx | 角速度 Angular velocity ω ⃗ = v ⃗ × r ⃗ ∣ r ⃗ ∣ 2 \vec{\omega}=\frac{\vec{v} \times \vec{r}}{|\vec{r}|^2} ω=∣r∣2v×r |
| 加速度 Acceleration a ⃗ = d v ⃗ d t = d 2 x ⃗ d t 2 \vec{a}=\frac{\mathrm{d} \vec{v}}{\mathrm{~d} t}=\frac{d^2 \vec{x}}{d t^2} a= dtdv=dt2d2x | 角加速度 Angular acceleration α ⃗ = d ω ⃗ d t = a ⃗ × r ⃗ ∣ r ⃗ ∣ 2 \vec{\alpha}=\frac{\mathrm{d} \vec{\omega}}{\mathrm{d} t}=\frac{\vec{a} \times \vec{r}}{|\vec{r}|^2} α=dtdω=∣r∣2a×r |
| 质心 Mass M = ∑ m i M=\sum m_i M=∑mi | 转动惯量 Inertia tensor I = R ⋅ I 0 ⋅ R T \mathbf{I}=\mathbf{R} \cdot \mathbf{I}_{\mathbf{0}} \cdot \mathbf{R}^{\mathrm{T}} I=R⋅I0⋅RT |
| 动量 Momentum p ⃗ = M v ⃗ \vec{p}=M \vec{v} p=Mv | 角动量 Angular momentum L ⃗ = I ω ⃗ \vec{L}=\mathbf{I} \vec{\omega} L=Iω |
| 力 Force F ⃗ = d p ⃗ d t = m a ⃗ \vec{F}=\frac{d \vec{p}}{d t}=m \vec{a} F=dtdp=ma | 力矩 Torque τ ⃗ = d L ⃗ d t \vec{\tau}=\frac{d \vec{L}}{d t} τ=dtdL |
Collision Detection
- 碰撞检测:东西是否撞上了
| 碰撞检测的两个阶段 | 方法 | |
|---|---|---|
| 粗筛 | 1. 直接用AABB找到相交的刚体 2. 找到潜在的重叠刚体对 | 1. BVH Tree 2. Sort and Sweep |
| 细筛 | 1. 进一步检测重叠 2. 得到相交信息 1. 相交点 2. 相交法线 3. 穿透深度 | 1. Basic Shape Intersection Test 2. MinkowskiDifference-based Methods 3. Separating Axis Theorem |
- Basic Shape Intersection Test
| 圆与圆碰撞 | 圆与胶囊体碰撞 | 胶囊体与胶囊体碰撞 |
|---|---|---|
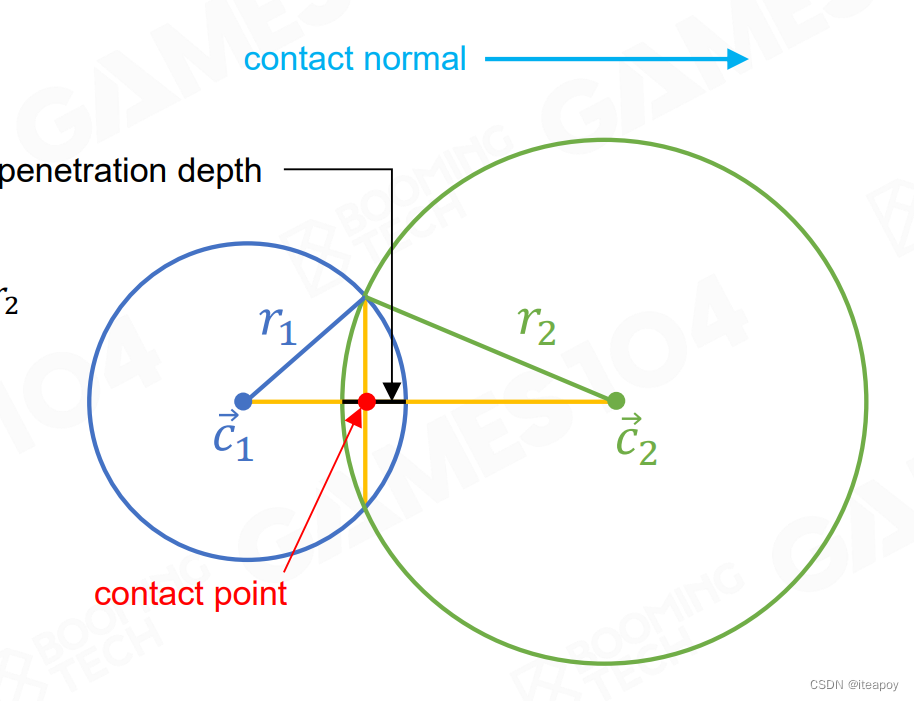 | 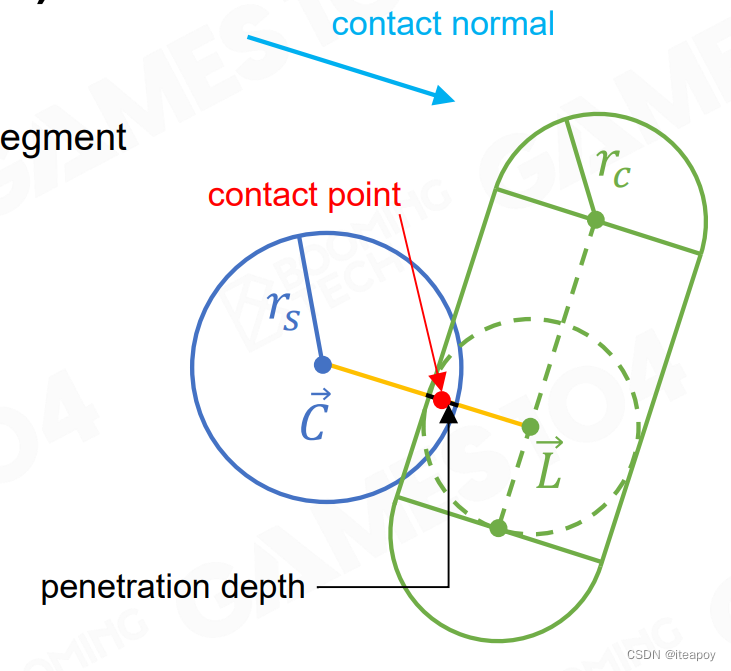 | 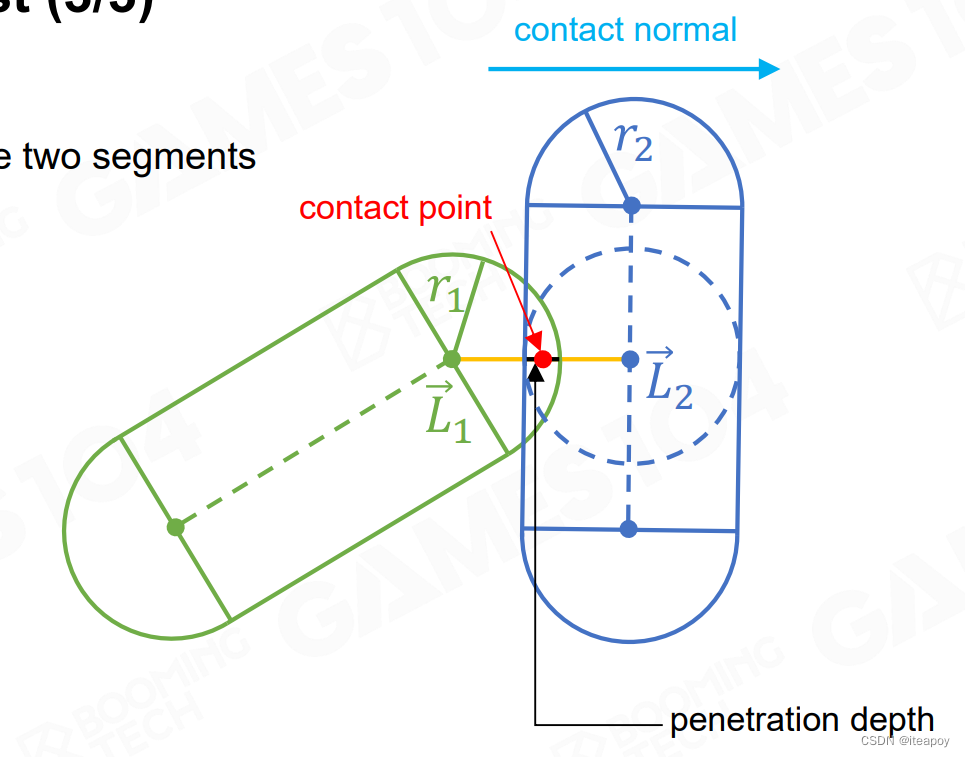 |
- MinkowskiDifference-based Methods
| 碰撞 | 未碰撞 |
|---|---|
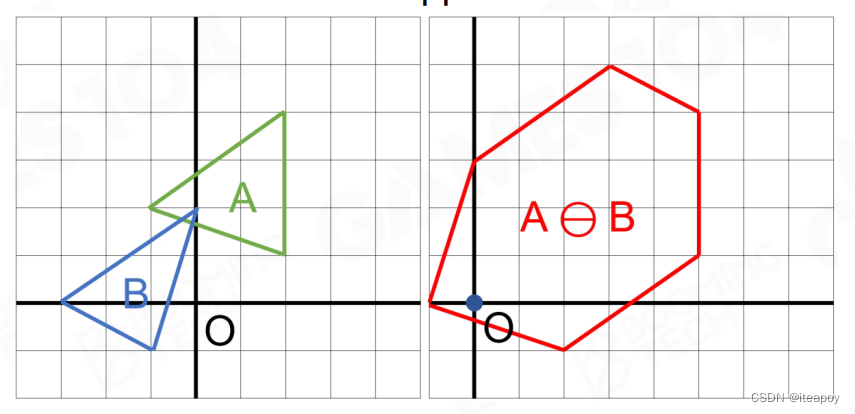 | |
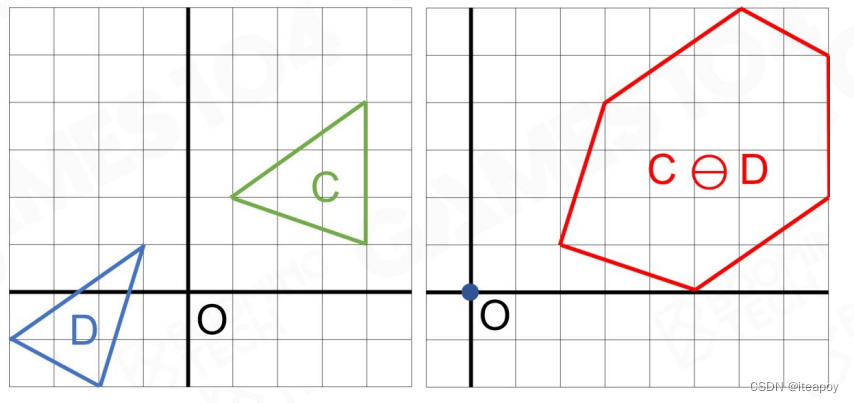 | |
- Separating Axis Theorem(SAT)
- 一定能找到一根轴,分离两个凸包
| 碰撞 | 不碰撞 | |
|---|---|---|
| 2D 情况 | 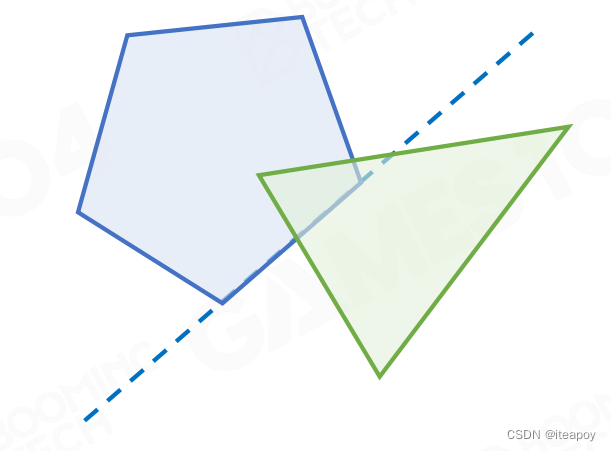 | 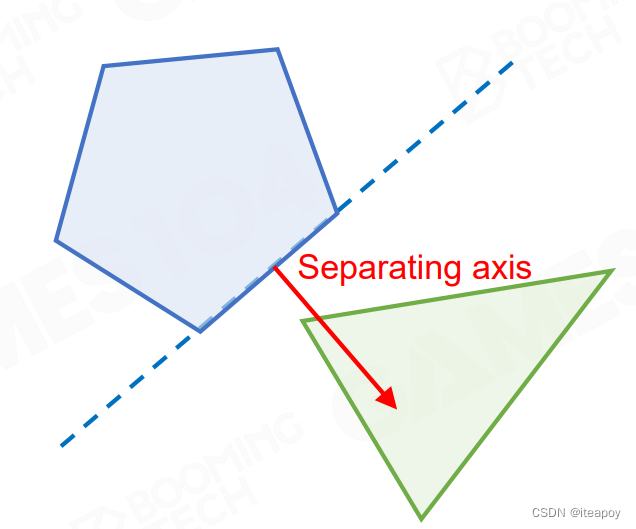 |
| 3D 情况 | 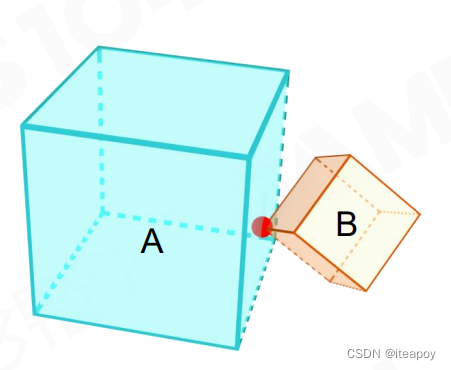 | 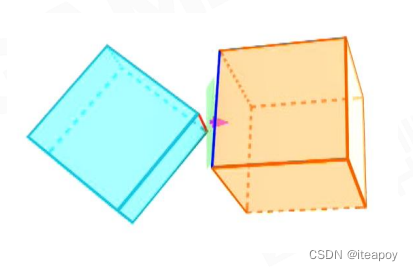 |
- 连续碰撞检测 Continuous Collision Detection(CCD)
Collision Resolution
- 如何处理碰撞?分离
| 方法 | 具体方法 | |
|---|---|---|
| 加入Penalty Force分离 | 加一个反向的惩罚力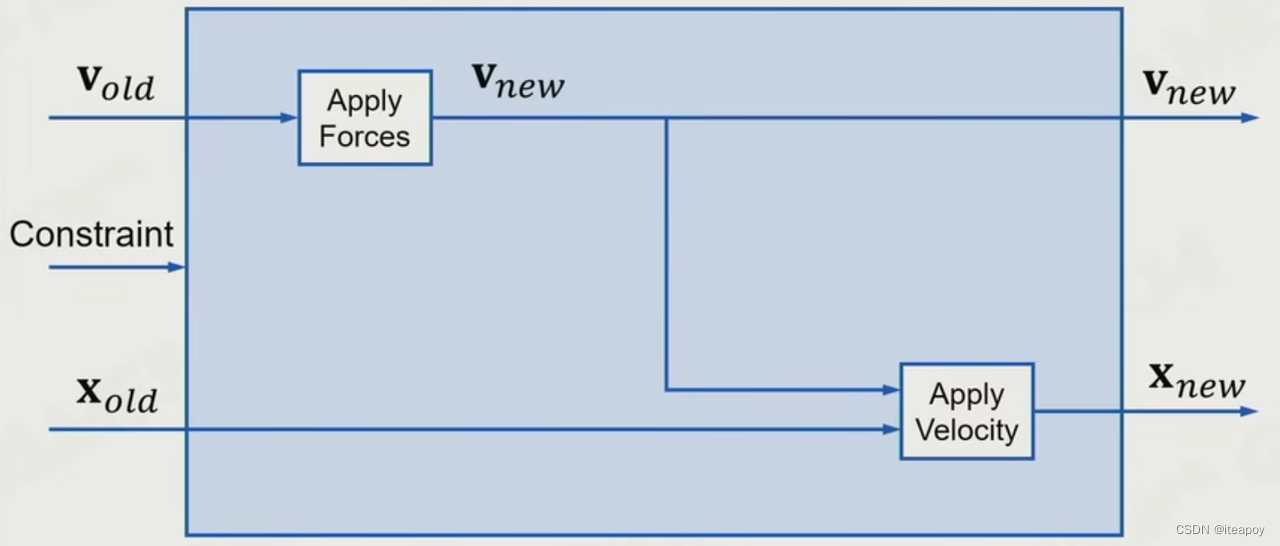 | |
| 转为约束问题 | 解决速度约束 | 不断尝试给一个冲量 |
| 解决位置约束 | 见 ragdoll - joint constraints |
应用与实践
Character controller
- 反物理的系统:摩擦力无穷大
- 用 Kinematic Actor
- 不受物理规则影响
- 推动别的物体
- 形状
- 双层胶囊
- Sweep test
- 与物体碰撞后,往旁边平移
- Stepping 爬楼梯
- 尝试往上提,再往前走
Ragdoll
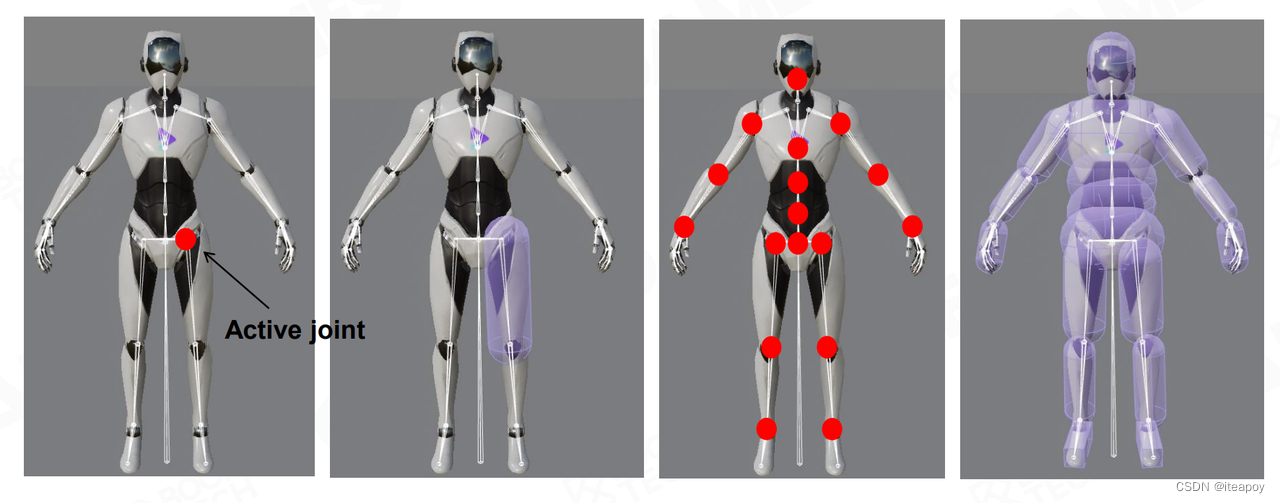
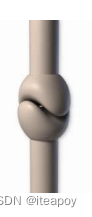
- 人体的 joint 约束(joint constraints)
| Hinge 铰链 | Ball-and-socket 球窝 | Pivot 枢轴 | Saddle 鞍状 | Condyloid 髁状突 | Gliding 滑行 |
 |  |  |  |  |  |
相关文章:

GAMES104-现代游戏引擎:从入门到实践 - 物理引擎课程笔记汇总
文章目录 0 入门资料1 物理引擎基本概念Actor & shapesRigid body dynamicsCollision DetectionCollision Resolution 应用与实践Character controllerRagdoll 0 入门资料 GAMES104-现代游戏引擎:从入门到实践_课程视频_bilibiliGAMES104官方账号 - 知乎课程主页…...

【linux】Xorg的工作原理
介绍 在linux系统上执行nvidia-smi时,总有一个进程占用gpu。 1 N/A N/A 2174 G /usr/lib/xorg/Xorg 4MiB /usr/lib/xorg/Xorg 是与X Window System(简称X11或X)相关的一个应用程序。X Window System是一个…...

02-docker下部署seata
官方部署文档 http://seata.io/zh-cn/docs/ops/deploy-by-docker 配置参数说明 http://seata.io/zh-cn/docs/user/configurations 1、镜像拉取 docker pull seata-server2、复制配置文件 mkdir /home/server/seata cd /home/server/seata docker run -d -p 8091:8091 -p 709…...
回归预测 | Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测
回归预测 | Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测 目录 回归预测 | Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测预测效果基本描述程序设计参考资料 预测效果 基本描述 1.Matlab实现GA-APSO-MBP、GA-MBP、MBP、BP多输入单输出回归预测&…...

精益生产咨询背后的秘密:企业如何实现价值最大化
精益生产,起源于丰田生产系统,是一种集中于削减浪费、优化流程、提升顾客价值的生产方法。它的核心在于确保每一步生产过程都能为顾客创造价值。以下是实现精益生产咨询的详细步骤: 1.确定客户价值 一切从顾客需求出发。企业需深入理解顾客…...

创建SERVLET
创建SERVLET 要创建servlet,需要执行以下任务: 编写servlet。编译并封装servlet。将servlet部署为Java EE应用程序。通过浏览器访问servlet。编写servlet 要编写servlet,需要扩展HttpServlet接口的类。编写servlet是,需要合并读取客户机请求和返回响应的功能。 读取和处…...
python算法与数据结构(搜索算法和拓扑排序算法)---深度优先搜索
课程目标 了解树/图的深度遍历,宽度遍历基本原理;会使用python语言编写深度遍历,广度遍历代码;掌握拓扑排序算法 搜索算法的意义和作用 搜索引擎 提到搜索两个子,大家都应该会想到搜索引擎,搜索引擎的基…...

thinkphp5实战之phpstudy v8环境搭建,解决Not Found找不到路径问题
引言 thinkphp以快速、简约的大道至简的思想广受欢迎,适合开发小型项目。本地环境下,phpstudy v8是一款比较优秀的集成环境软件。部署完项目后,访问的时候傻眼,报错。 解决方案 不要慌,这个是伪静态的原因。选择apach…...
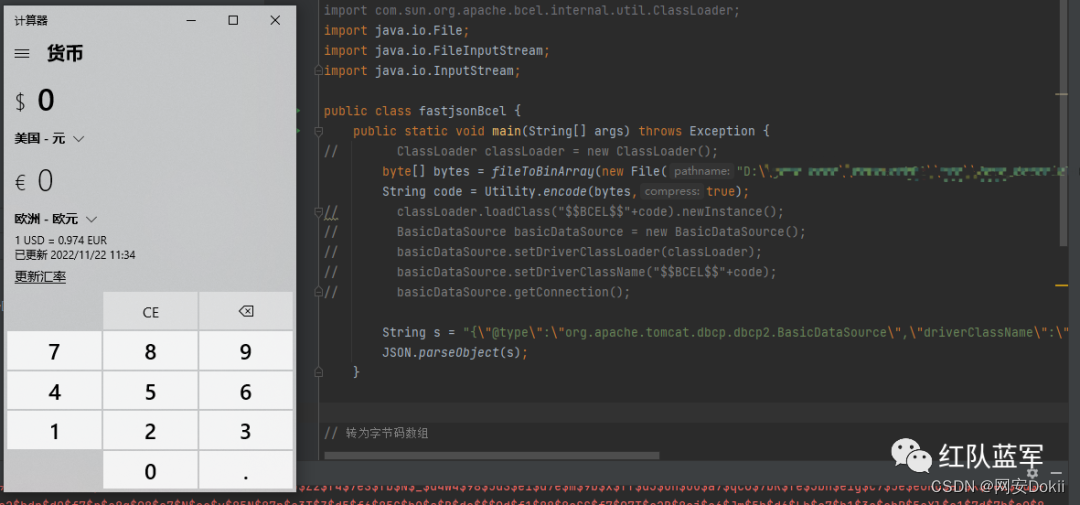
fastjson-BCEL不出网打法原理分析
FastJson反序列化漏洞 与原生的 Java 反序列化的区别在于,FastJson 反序列化并未使用 readObject 方法,而是由 FastJson 自定一套反序列化的过程。通过在反序列化的过程中自动调用类属性的 setter 方法和 getter 方法,将JSON 字符串还原成对…...

部署mysql主从同步,部署mysql数据读写分离结构+mycat2
主要命令 [rootmysql59 ~]# yum –y install mysql-server mysql[rootmysql59 ~]# systemctl start mysqld[rootmysql59 ~]# vim /etc/my.cnf.d/mysql-server.cnf[mysqld]server-id59log-binmysql59:wq[rootmysql59 ~]# systemctl restart mysqld//用户授权[rootmysql59 ~]# my…...

【最新!超详细C++入门】
01_C语言基础 一、课程目标 1、掌握 C基本语法:变量、常量、注释、标识符命名规范 2、掌握C数据类型 3、掌握C的输入和输出 4、掌握C运算符和表达式 5、掌握条件语句 6、掌握循环语句 二、课程内容 1 C初识 1.1 第一个C程序 编写一个C程序总共分为4个步骤…...

【Linux】【实战系列】10 分钟掌握日常开发中 Linux 网络处理相关命令
文章目录 lsofnetstatpingnslookupsshssh-keygenscpsftp 网络工具 curl网络工具 wget最后个人简介 hello,大家好,我是 Lorin,上一期和大家分享一期日常开发中常用的 Linux 文件和文本命令实战教学,这一期给大家带来常用的网络处理…...
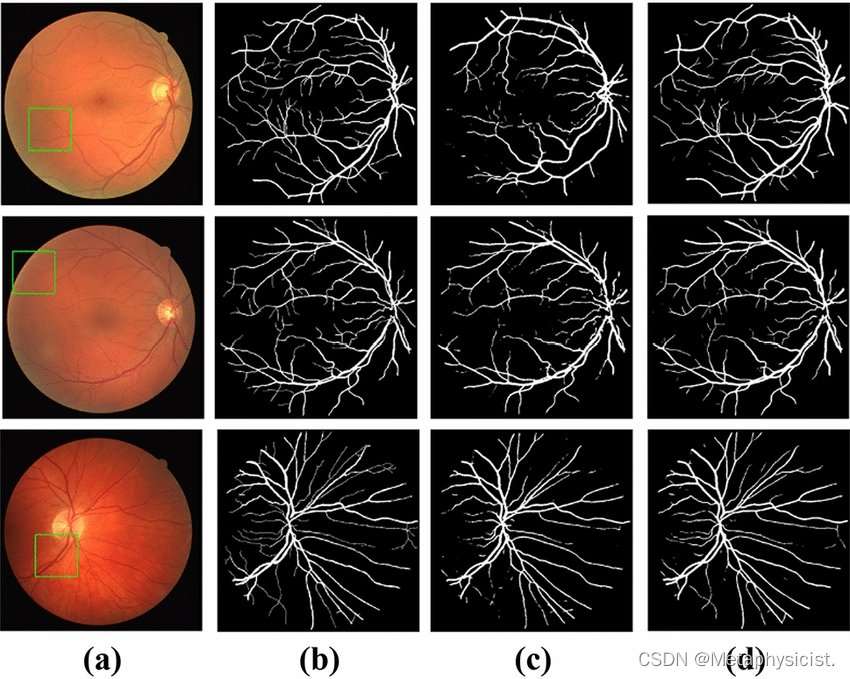
语义分割常用评价指标
在图像处理领域中,语义分割是很重要的一个任务。在实际项目开发中,评估模型预测效果以及各指标的含义对于优化模型极为重要。 本文将主要评价指标的计算算法进行了详细说明,并加上注释解释每个指标的含义。这对理解各指标背后的数学原理以及能否在实践中应用或许有…...

从0开始学习C++ 第一课:你的第一个C++程序
第一课:你的第一个C程序 当然可以。让我们从C的基础开始,我们的第一课将覆盖以下几个主题: 程序结构编写和运行你的第一个C程序基本的输入输出(I/O) 第一课:你的第一个C程序 在C中,所有的程…...
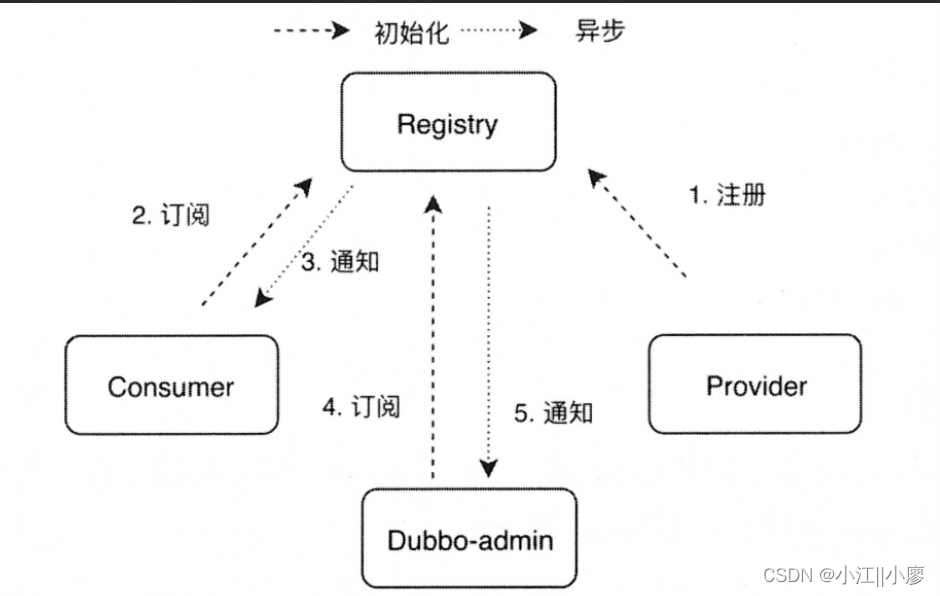
Dubbo-admin监控中心
监控中心 Dubbo-admin监控中心执行操作启动provider和consumer项目进行测试总体流程 Dubbo-admin监控中心 dubbo-admin下载路径 git clone https://github.com/apache/dubbo-admin.git图1-1 dubbo-admin项目文件展示 执行操作 # 启动zookeeper# 前端 cd dubbo-admin-ui npm i…...
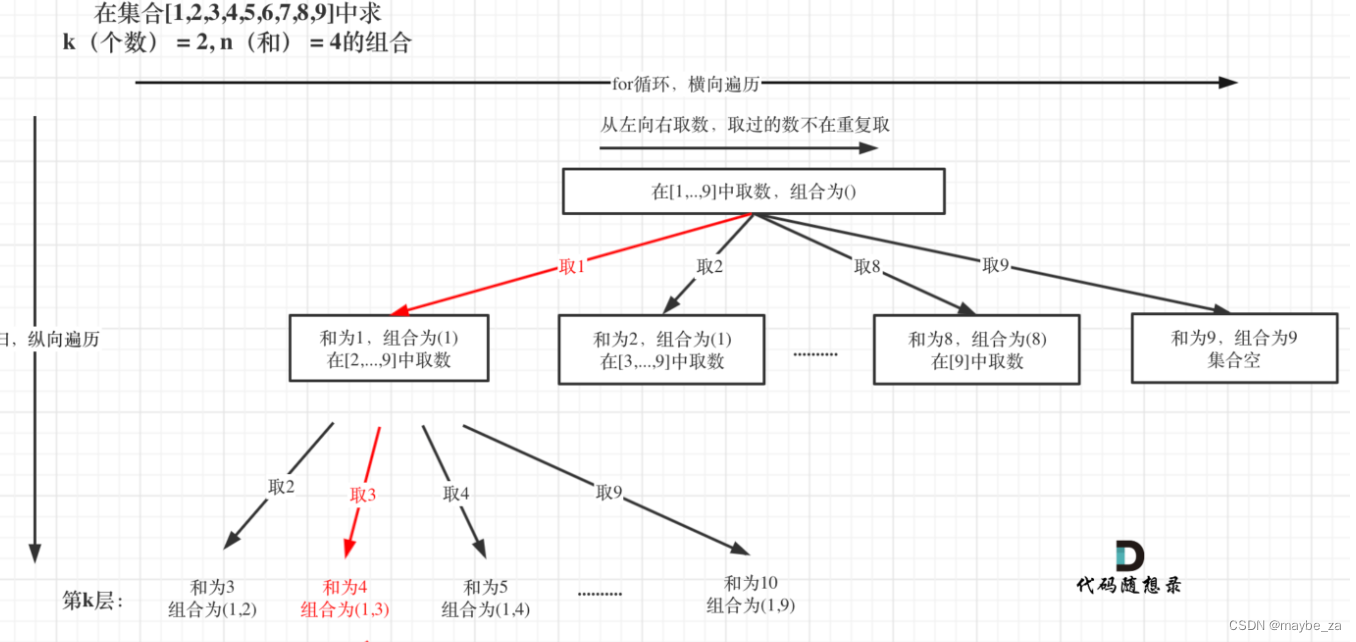
216. 组合总和 III - 力扣(LeetCode)
题目描述 找出所有相加之和为 n 的 k 个数的组合,且满足下列条件: 只使用数字1到9每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 输入示例 k 3, n 7输出示例 [[1,2,…...
 时间插入、删除和获取随机元素)
LeetCode-题目整理【5】:O(1) 时间插入、删除和获取随机元素
RandomizedSet结构体存在切片和哈希表的原因: 变长数组由于可以根据下标定位到特定元素,因此可以在 O(1)的时间内完成获取随机元素操作,但是由于无法在 O(1) 的时间内判断元素是否存在,因此不能在 O(1) 的时间内完成插入和删除操作…...

服务器感染了.wis[[Rast@airmail.cc]].wis勒索病毒,如何确保数据文件完整恢复?
导言: 在当今数字化的时代,恶意软件攻击已经变得越来越复杂和狡猾,[[MyFilewaifu.club]].wis [[backupwaifu.club]].wis[[Rastairmail.cc]].wis勒索病毒是其中的一种新威胁。本文91数据恢复将深入介绍[[MyFilewaifu.club]].wis [[backupwaif…...

ContentNegotiationManagerFactoryBean 内容协商
一.什么是内容协商 简单点说,就是同一资源,可以有多种表现形式,比如xml、json等,具体使用哪种表现形式,是可以协商的。 这是RESTfull的一个重要特性,Spring Web MVC也支持这个功能。 1.Spring MVC REST是如何决定采用…...

html css js 开发一个猜数字游戏
以下是一个使用HTML、CSS和JS开发的简单猜数字游戏的示例: HTML代码: <!DOCTYPE html> <html> <head><title>猜数字游戏</title><link rel"stylesheet" type"text/css" href"style.css&quo…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
