跳跃游戏-算法
题目
给定一个数组nums = {1,2,3,4,5},每个元素nums[i]表示从i这个位置最多可以向前跳跃nums[i]个台阶,求最小需要跳几次就可以调到末尾
思路
反向查找
从末尾开始逐个向前判断最远的起跳位置,接着再以该位置递归的判断
public int jumpToTheEndWithMinSteps(int[] nums){int position = nums.length-1;int steps = 0;while(position>0){for(int i=0;i<position;i++){if(i+nums[i]>=position){position = i;steps++;break; } } }return steps;
}效果
时间复杂度:O(n^2)
空间复杂度:O(1)
正向查找
从i=0位置开始向后找,每次在当前最远位置如i,计算从i开始跳跃空间nums[i]内这个区间内能够跳的最远位置是哪里,然后以此类推
public int jumpToTheEndWithMinSteps(int[] nums){int length = nums.length;int end = 0;int maxPosition = 0;int steps = 0;for(int i=0;i<length;i++){//计算i<j<=end区间内能够跳的最远的位置,将其记录为maxPositionmaxPosition = Math.max(maxPosition,i+nums[i]);//每次区间结束,都更新一下最新调的最远的位置if(i==end){end = maxPosition;steps++; } }return steps;
}效果
时间复杂度:O(n)
空间复杂度:O(1)
相关文章:

跳跃游戏-算法
题目 给定一个数组nums {1,2,3,4,5},每个元素nums[i]表示从i这个位置最多可以向前跳跃nums[i]个台阶,求最小需要跳几次就可以调到末尾 思路 反向查找 从末尾开始逐个向前判断最远的起跳位置,接着再以该位置递归的判断 public int jumpT…...
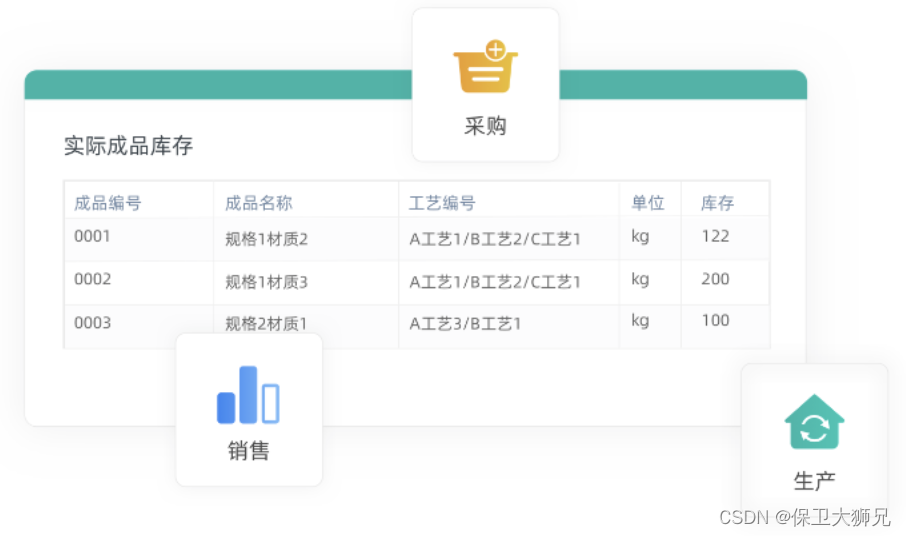
ERP系统哪个好用?用友,金蝶,ORACLE,SAP综合测评
ERP系统哪个好用?用友,金蝶,ORACLE,SAP综合测评 ERP领域SAP、ORACLE相对于国内厂商如用友、金蝶优势在哪? SAP,ORACLE操作习惯一般国人用不惯;相对于国产软件,界面也很难看&#x…...

外汇天眼:美国证券交易委员会(SEC)采纳了一系列规定,以加强与特殊目的收购公司(SPACs)相关的投资者保护
美国证券交易委员会(SEC)今天通过了一系列新规和修订,以增强特殊目的收购公司(SPACs)的首次公开募股(IPOs)中的披露,并在SPACs与目标公司之间的后续业务合并交易(de-SPAC…...

kotlin map 与 flatmap
kotlin map 与 flatmap 是2个不同的概念的 map 是一种数据结构,flatmap 是一个高阶函数,处理集合用的 Map Map 是一种数据结构,它由一系列的键值对组成,每个键都是唯一的,并且与一个特定的值相关联。你可以通过键来…...
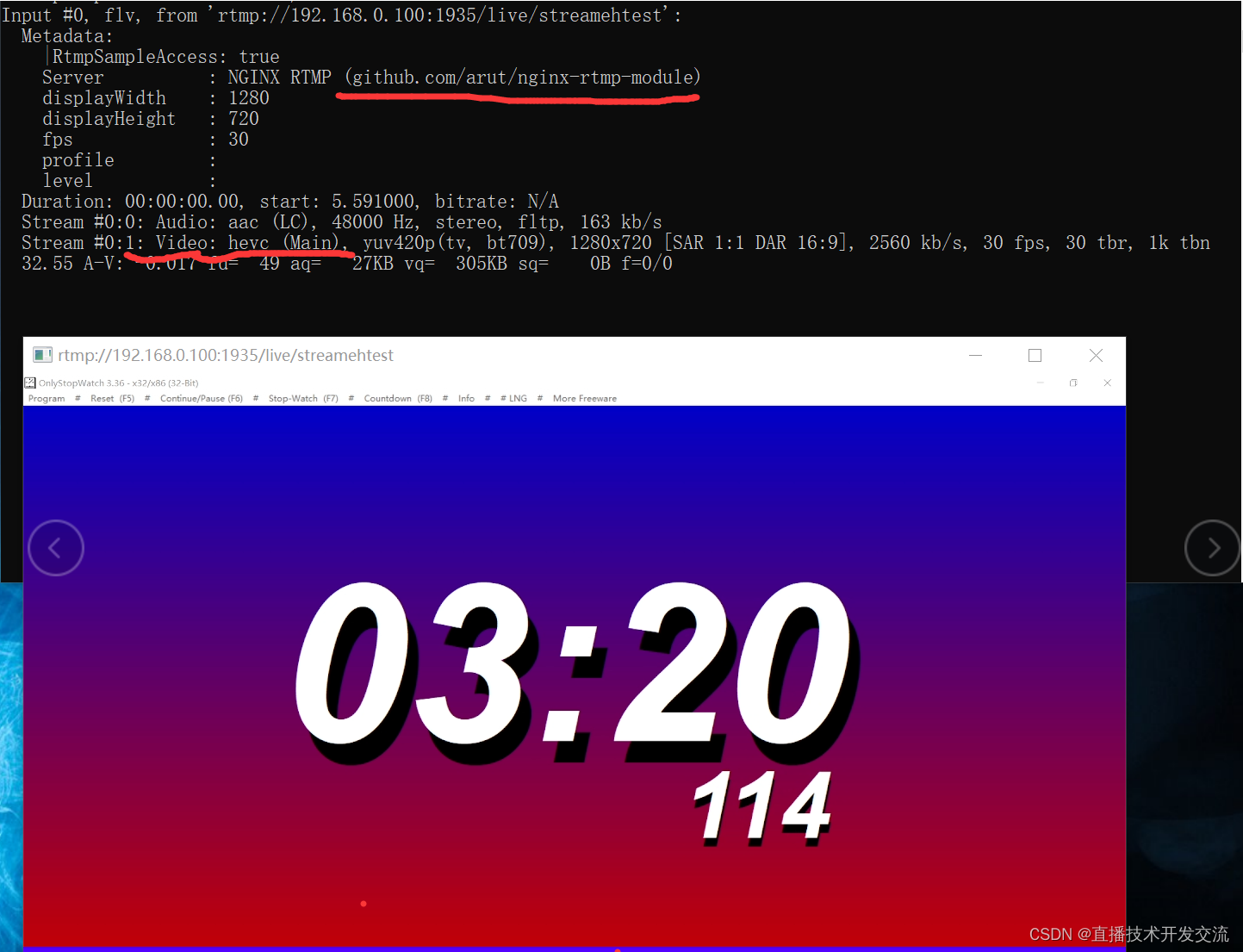
nginx-rtmp-module 支持 Enhancing RTMP HEVC(H.265)
Enhancing RTMP, FLV 2023年7月31号正式发布,主要支持了HEVC(H.265)、VP9、AV1视频编码,发布差不多半年了,很多开源项目已支持,最近打算播放和推送端也支持下,想找个支持的rtmp server方便测试用,但没找到合…...

2024最新JDK1.8+JDK17+JDK21安装包下载+文档
2024年更新,JDK8的64位和32位安装包都有,Java8最新文档也有,JDK17和JDK21的最新安装包也有 因为网上的安装包都不是最新的,所以自己去Oracle官网登录下载保存了一份,需要的朋友下面网盘链接下载 JDK8—64位安装程序&…...

如何利用chatgpt提升工作效率
chatgpt全领域小助手 项目管理:制定项目计划、跟踪进度、分配任务和记录里程碑。客户服务:回答常见问题、提供产品支持和处理客户投诉,提升客户满意度。销售支持:提供销售培训、销售脚本和客户资料,辅助销售团队进行销…...
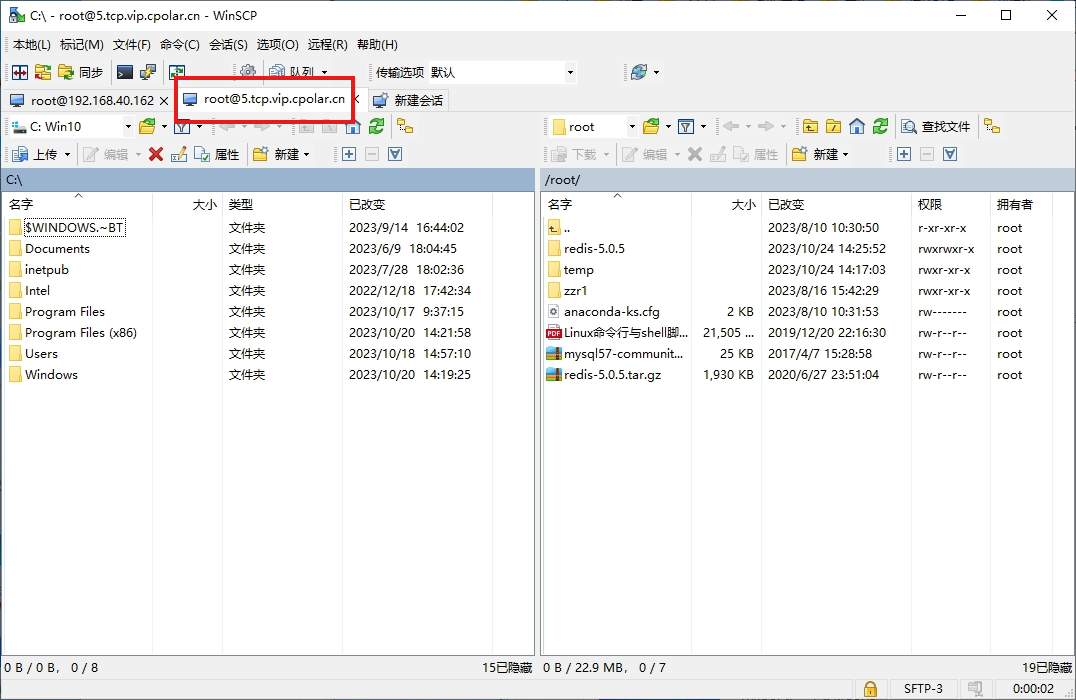
WinSCP下载安装并实现远程SSH本地服务器上传文件
文章目录 1. 简介2. 软件下载安装:3. SSH链接服务器4. WinSCP使用公网TCP地址链接本地服务器5. WinSCP使用固定公网TCP地址访问服务器 1. 简介 Winscp是一个支持SSH(Secure SHell)的可视化SCP(Secure Copy)文件传输软件,它的主要功能是在本地与远程计…...

QEMU搭建arm虚拟机开发环境
获取QEMU代码 git clone https://gitlab.com/qemu-project/qemu.git 切换对应的工程分支 使用git指令切换到对应的分支上,我这里使用的是stable-4.0的分支 git checkout -b stable-4.0 remotes/origin/stable-4.0 配置&编译 在工程的根目录下执行 ./conf…...

web 应用常见的安全问题
一xss攻击 人们经常将跨站脚本攻击(Cross Site Scripting)缩写为CSS,但这会与层叠样式表(Cascading Style Sheets,CSS)的缩写混淆。因此,有人将跨站脚本攻击缩写为XSS。 跨站脚本攻击ÿ…...

502. IPO
502. IPO 题目链接:502. IPO 代码如下: //堆的使用 class Solution { public:int findMaximizedCapital(int k, int w, vector<int>& profits, vector<int>& capital) {vector<pair<int,int>> mp;//优先队列默认的是大…...
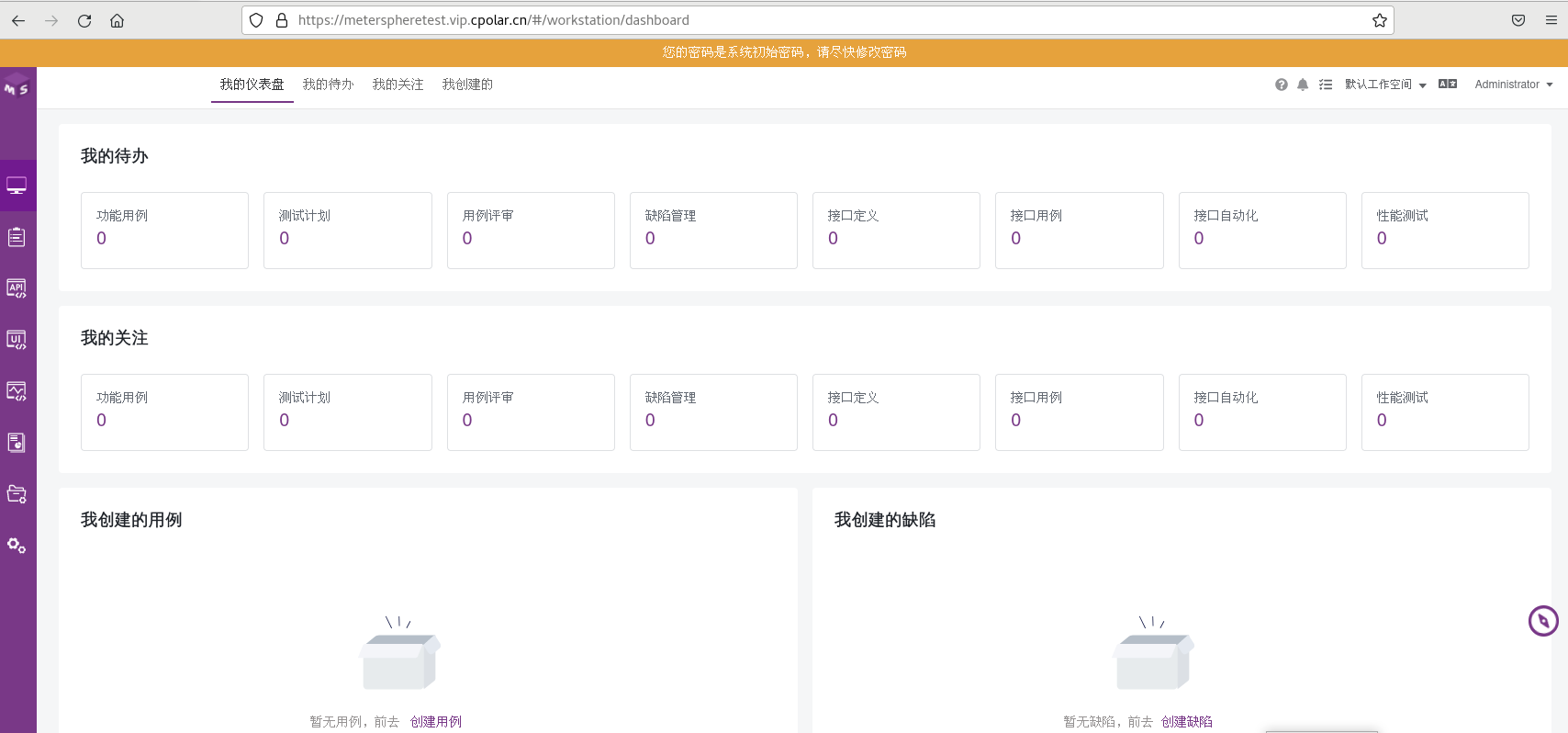
如何安装MeterSphere并实现无公网ip远程访问服务管理界面
文章目录 前言1. 安装MeterSphere2. 本地访问MeterSphere3. 安装 cpolar内网穿透软件4. 配置MeterSphere公网访问地址5. 公网远程访问MeterSphere6. 固定MeterSphere公网地址 正文开始前给大家推荐个网站,前些天发现了一个巨牛的 人工智能学习网站, 通…...

做FP独立站怎么引流?这个引流法宝收好了!
近年来,由于卖家数量飙升导致平台竞争持续升级,卖家之间的恶性循环竞争以及平台政策的不断调整等,造成了众多亚马逊等跨境卖家纷纷从平台转向独立站。可是,转型做独立站前要先考虑清楚独立站与平台二者之间的区别。 如果在第三方平…...

幻兽帕鲁PalWorld服务器搭建教程,1分钟开服,纯小白教程,无需基础
雨云面板服快速开幻兽帕鲁PalWorld服务器的教程,配置文件修改方法和配置项中文注释。 最近这游戏挺火,很多人想跟朋友联机,如果有专用服务器,就不需要房主一直开着电脑,稳定性也好得多。 幻兽帕鲁简介 《幻兽帕鲁》…...

算法小抄01
1. 计数排序是一种基于 统计 的排序算法 2. 基于比较的排序算法有:(1)直接插入排序;(2)冒泡排序;(3)简单选择排序;(4)希尔排序&#…...
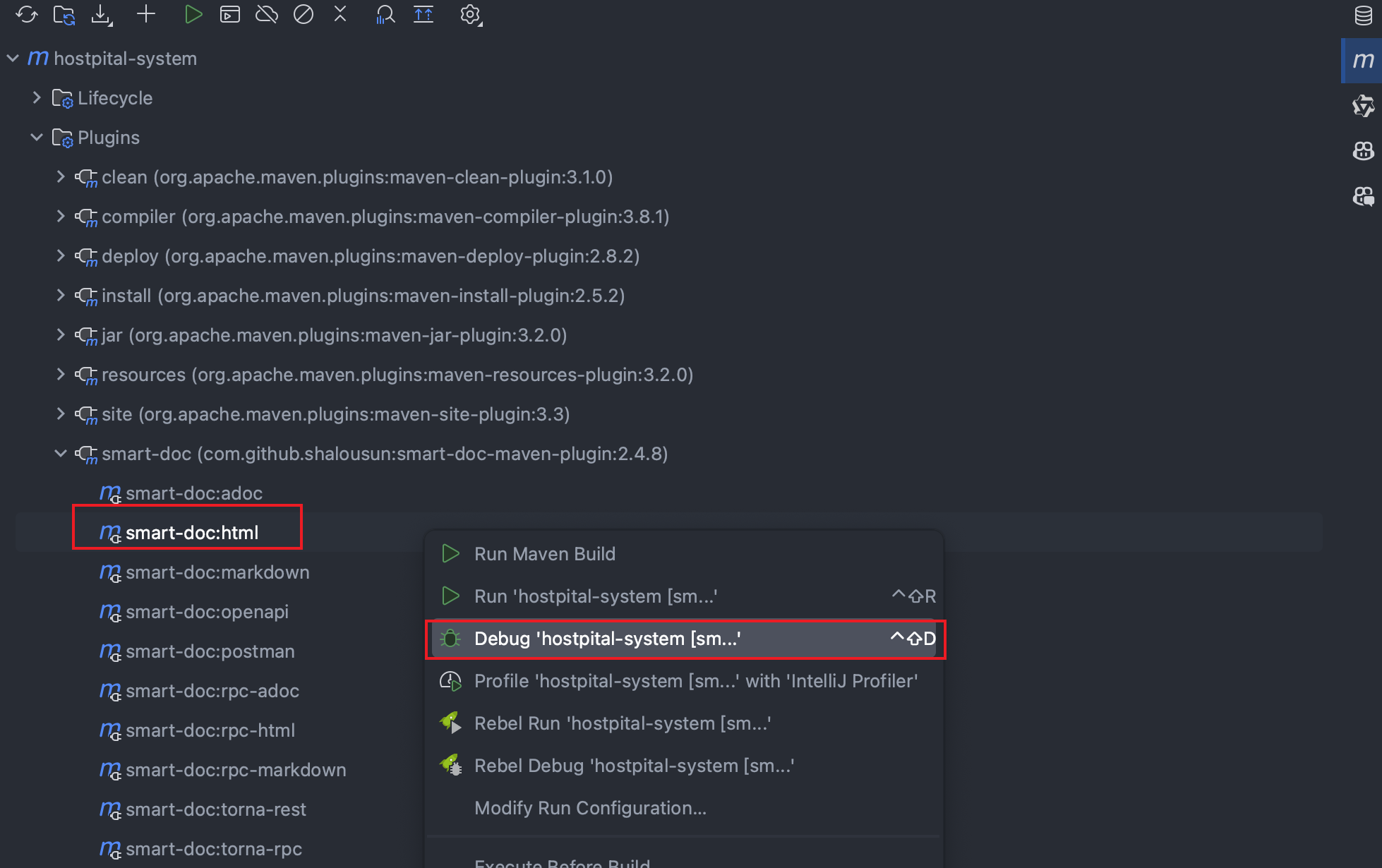
Spring Boot 集成 API 文档 - Swagger、Knife4J、Smart-Doc
文章目录 1.OpenAPI 规范2.Swagger: 接口管理的利器3.Swagger 与 SpringFox:理念与实现4.Swagger 与 Knife4J:增强与创新5.案例:Spring Boot 整合 Swagger35.1 引入 Swagger3 依赖包5.2 优化路径匹配策略兼容 SpringFox5.3 配置 Swagger5.4 S…...

2024年软考报名时间及条件,小白必看
不少考生开始准备报名2024年软件水平考试,那么报名软考有没有学历、专业以及工作经验等方面的限制呢?今天就给大家梳理下2024年软考考试,若有变更,也会及时更新内容。 免费送备考资料。联系我 2024年软考考试时间 2024年软考有两次考试&a…...

vue 跨域XMLHttpRequest
vue 跨域 使用XMLHttpRequest 亲测好使 let url=http://127.0.0.1:9000/pssnotifyyb?b=1//url=https://api.j4u.ink/v1/store/other/proxy/remote/moyu.jsonvar xhr=new XMLHttpRequest()xhr.open(GET,url,true)//第三个参数是是否异步请求,默认true xhr.onreadyst…...
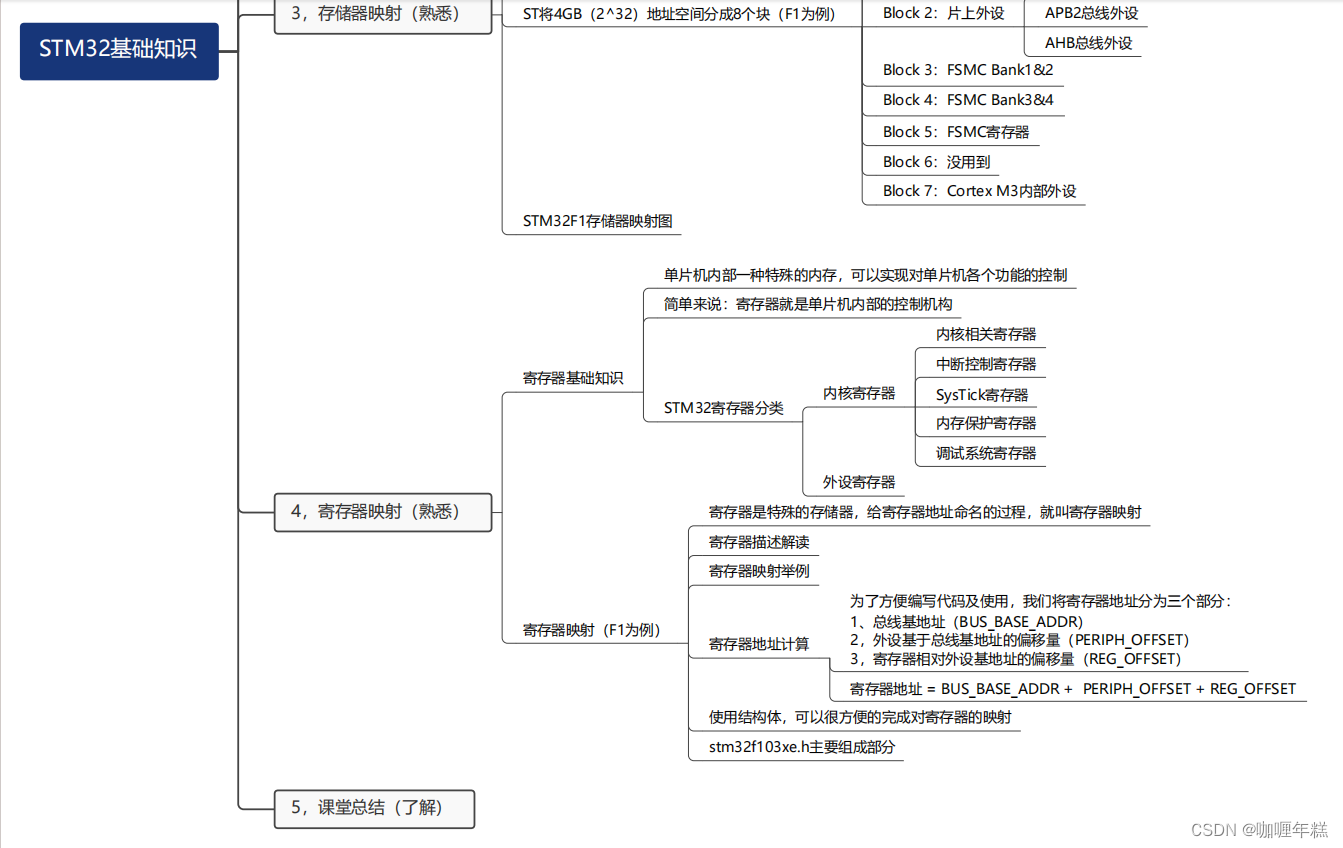
【正点原子STM32】STM32基础知识(F1F4F7H7 STM32系统框架、寻址范围、存储器映射的存储器功能划分、寄存器映射)
一、STM32系统框架 1.1、Cortex M内核 & 芯片1.2、F1系统架构1.3、F4系统架构1.4、F7系统架构1.5、H7系统架构 二、STM32的寻址范围? 三、存储器映射 存储器功能划分(F1为例)STM32F1存储器映射图 四、寄存器映射 寄存器基础知识STM3…...

Oracle、MySQL数据库常规命令语法-简易记录(非常规持续更新)
前言:呈现的是非常基础必备命令以及常规关联语法,因涉及到不同数据库其表达都会有所区别,此篇纯属做个仓库记录更非常规持续更新,专业人士可忽略,且看且珍惜… MySQL: 关系型数据库、重点开源、支持大型规模、标准SQL数据语言、多平台多架构、高可用集群、可定制开发等等、…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
