解决TSP旅行商问题3个可以用Python编程的优化路径算法
旅行商问题(Traveling Salesman Problem, TSP)是一个经典的组合优化问题,它要求找到访问一系列城市并返回起点的最短可能路线,同时每个城市仅访问一次。这个问题是NP-hard的,意味着没有已知的多项式时间复杂度的精确算法来解决它。尽管如此,仍然有许多启发式算法和元启发式算法可以用来找到接近最优解的解。6547网提供以下是三种可以用Python编程来解决TSP问题的算法,以及它们的编程难度级别、时间复杂度和所需的库:
-
最近邻算法(Nearest Neighbor Algorithm)
编程难度级别:初级
时间复杂度:O(n^2),其中n是城市的数量
所需库:无,标准Python库即可
import numpy as np import sys def nearest_neighbor(distances): num_cities = len(distances) tour = [0] # 假设从城市0开始 for _ in range(num_cities - 1): current_city = tour[-1] next_city = np.argmin(distances[current_city]) tour.append(next_city) tour.append(tour[0]) # 回到起点 return tour
2.遗传算法(Genetic Algorithm)
编程难度级别:中级
时间复杂度:依赖于实现和迭代次数,通常是O(n * gen_count * pop_size),其中gen_count是迭代次数,pop_size是种群大小
所需库:deap 或 ga
from deap import base, creator, tools, algorithms # 创建问题相关的数据结构
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin) # 初始化种群和遗传算法参数
toolbox = base.Toolbox()
toolbox.register("attr_city", random.randint, 0, len(distances) - 1)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_city, n=len(distances))
toolbox.register("population", tools.initRepeat, list, toolbox.individual) # 定义适应度函数和遗传操作
def evaluate(individual): route_distance = calculate_route_distance(individual, distances) return route_distance, toolbox.register("evaluate", evaluate)
toolbox.register("mate", tools.cxOrdered, indpb=0.5)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3) # 运行遗传算法
pop = toolbox.population(n=pop_size)
hof = tools.HallOfFame(1)
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", np.mean, axis=0)
stats.register("min", np.min, axis=0)
stats.register("max", np.max, axis=0) pop, logbook = algorithms.eaSimple(pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=ngen, stats=stats, halloffame=hof, verbose=True) # 返回最佳解
best_ind = hof[0]
best_route = [0] + best_ind + [0] # 添加起始城市并闭合路线
return best_route
3.模拟退火算法(Simulated Annealing)
编程难度级别:中级
时间复杂度:依赖于迭代次数和温度下降策略,通常是O(n * iterations)
所需库:标准Python库即可
import random import math def simulated_annealing(distances, initial_temp, final_temp, alpha, iterations): current_route = random.sample(range(len(distances)), len(distances)) current_route.append(current_route[0]) # 闭合路线 current_cost = calculate_route_distance(current_route, distances) best_route = current_route best_cost = current_cost temp = initial_temp for _ in range(iterations): new_route = current_route.copy() swap_indices = random.sample(range(1, len(new_route
相关文章:

解决TSP旅行商问题3个可以用Python编程的优化路径算法
旅行商问题(Traveling Salesman Problem, TSP)是一个经典的组合优化问题,它要求找到访问一系列城市并返回起点的最短可能路线,同时每个城市仅访问一次。这个问题是NP-hard的,意味着没有已知的多项式时间复杂度的精确算…...

10英寸安卓车载平板电脑丨ONERugged车载工业平板:解决农业工作效率
农业是人类社会的基石之一,而农业工作效率的提升一直是农民和农业专业人士关注的重要议题。随着技术的不断进步,车载工业平板成为了解决农业工作效率的创新解决方案。本文将探讨车载工业平板如何为农业带来巨大的改变,提高农民的工作效率和农…...

Mysql报错:too many connections
1 问题原因 MySQL报错“too many connections”通常是由于数据库的最大连接数超过了MySQL配置的最大限制。有以下几个原因: (1)访问量过高:当MySQL服务器面对大量的并发请求时,已经建立的连接数可能会不足以处理所有的请求,从而导致连接池耗尽、连接被拒绝、出现“too …...
1Panel面板如何安装并结合内网穿透实现远程访问本地管理界面
文章目录 前言1. Linux 安装1Panel2. 安装cpolar内网穿透3. 配置1Panel公网访问地址4. 公网远程访问1Panel管理界面5. 固定1Panel公网地址 前言 1Panel 是一个现代化、开源的 Linux 服务器运维管理面板。高效管理,通过 Web 端轻松管理 Linux 服务器,包括主机监控、…...
的Python导入pandas包,报错:ImportError: No module named ‘_bz2‘)
Linux(Debian系)的Python导入pandas包,报错:ImportError: No module named ‘_bz2‘
前言: 硬件操作系统国产化路漫漫,由此可见华为的厉害。 今天在香橙派上用自己编译的python导入pandas时,报错: from _bz2 import BZ2Compressor, BZ2Decompressor ImportError: No module named _bz2ImportError: No module name…...

React useEffect使用
第一 export default function App() { const [name,setname] useState(huhu) useEffect(()>{ setname(name.substring(0,1).toUpperCase()name.substring(1)) },[name]) //[name,age]//可以有多个参数 //带参数,第一次默认执行一次,第二次name更新…...
三网码支付系统源码,三网免挂有PC软件,有云端源码,附带系统搭建教程
搭建教程 1.先上传云端源码 然后配置Core/Config.php文件里面数据库信息注改;数据库帐号密码 2.云端源码里面Core/Api_Class/Instant_Url_List.php文件配置终端地址注改;第4 http://终端地址/ 3.导入云端数据库 账号admin 密码123456注改࿱…...

编程笔记 html5cssjs 073 JavaScript Object数据类型
编程笔记 html5&css&js 073 JavaScript Object数据类型 一、创建 Object二、Object 类型的属性与方法三、示例四、参考小结 JavaScript 中的 Object 数据类型是该语言中最复杂也最灵活的数据类型之一,它是其他所有内置对象和用户自定义对象的基础。在 JavaS…...
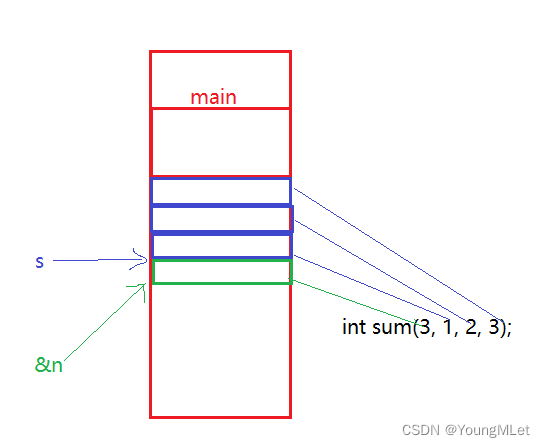
【Linux】基于管道进行进程间通信
进程间通信 一、初识进程间通信1. 进程间通信概念2. 进程间通信分类 二、管道1. 管道概念2. 管道原理3. 匿名管道4. 匿名管道系统接口5. 管道的特性和情况6. 匿名管道的应用(1)命令行(2)进程池 7. 命名管道(1ÿ…...

Vue中间件的讲解案例分析
Vue中间件的讲解案例分析 1. Axios中间件: Axios是一个常用的HTTP客户端,可以与Vue结合使用,处理网络请求和数据获取。您可以创建一个Axios实例,并将其作为Vue的原型属性或插件使用,以便在整个应用程序中共享和使用。…...

【C生万物】C语言分支和循环语句
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️ 🙏小杨水平有…...
Vue代理模式和Nginx反向代理(Vue代理部署不生效)
在使用axios时,经常会遇到跨域问题。为了解决跨域问题,可以在 vue.config.js 文件中配置代理: const { defineConfig } require(vue/cli-service) module.exports defineConfig({transpileDependencies: true,devServer: {port: 7070,prox…...

C语言中的作用域与生命周期
作用域(scope)是程设计概念,通常来说,一段程序代码中所⽤到的名字并不总是有效的,而限定这个名字的可⽤性的代码范围就是这个名字的作用域。 局部变量的作用域是变量所在的局部范围。全局变量的作用域是整个工程&…...

MATLAB计算多边形质心/矩心
前言:不规则四边形的中心 不规则四边形的出心有多种定义,以下是最常见的三种: 1.重心:重心是四边形内部所有顶点连线交点的平均位置。可以通过求解四个顶点坐标的平均值来找到重心。 2.质心:质心是四边形内部所有质点…...

IP地址如何保护网络安全
面对网络攻击时,仅依靠常态化的网络安全防御系统已捉襟见肘,如联合使用IP地址数据可以形成多元化的安全解决方案,全面监控网络活动,发现潜在威胁,制定有针对性的应对措施。 网络攻击追踪 当网站或应用遭受DDoS等网络攻…...
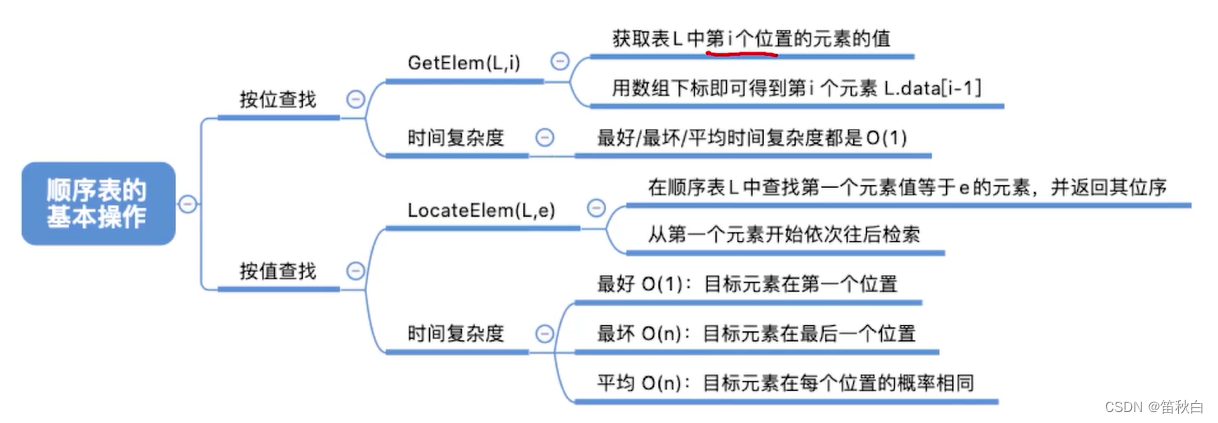
考研数据结构笔记(3)
顺序表存储结构 存储结构顺序结构定义基本操作的实现静态分配问题 动态分配代码功能 顺序表的特点: 顺序表小结顺序表的插入删除插入删除小结 顺序表的查找按位查找按值查找小结 存储结构 顺序结构 定义 线性表是具有相同数据类型的n(n>0)个数据元素的有限序列(每个数据元素…...

第二讲 数据结构 AcWing 827. 双链表
目录 双链表代码 && 思路 双链表 实现一个双链表,双链表初始为空,支持 5 种操作: 在最左侧插入一个数; 在最右侧插入一个数; 将第 k个插入的数删除; 在第 k 个插入的数左侧插入一个数;…...

假期作业 2月6号
一、填空题 1、一个类的头文件如下所示,num初始化值为5,程序产生对象T,且修改num为10,并使用show()函数输出num的值10。 #include <iostream.h> class Test { private: static int num; public: Test(int); void show(); };…...
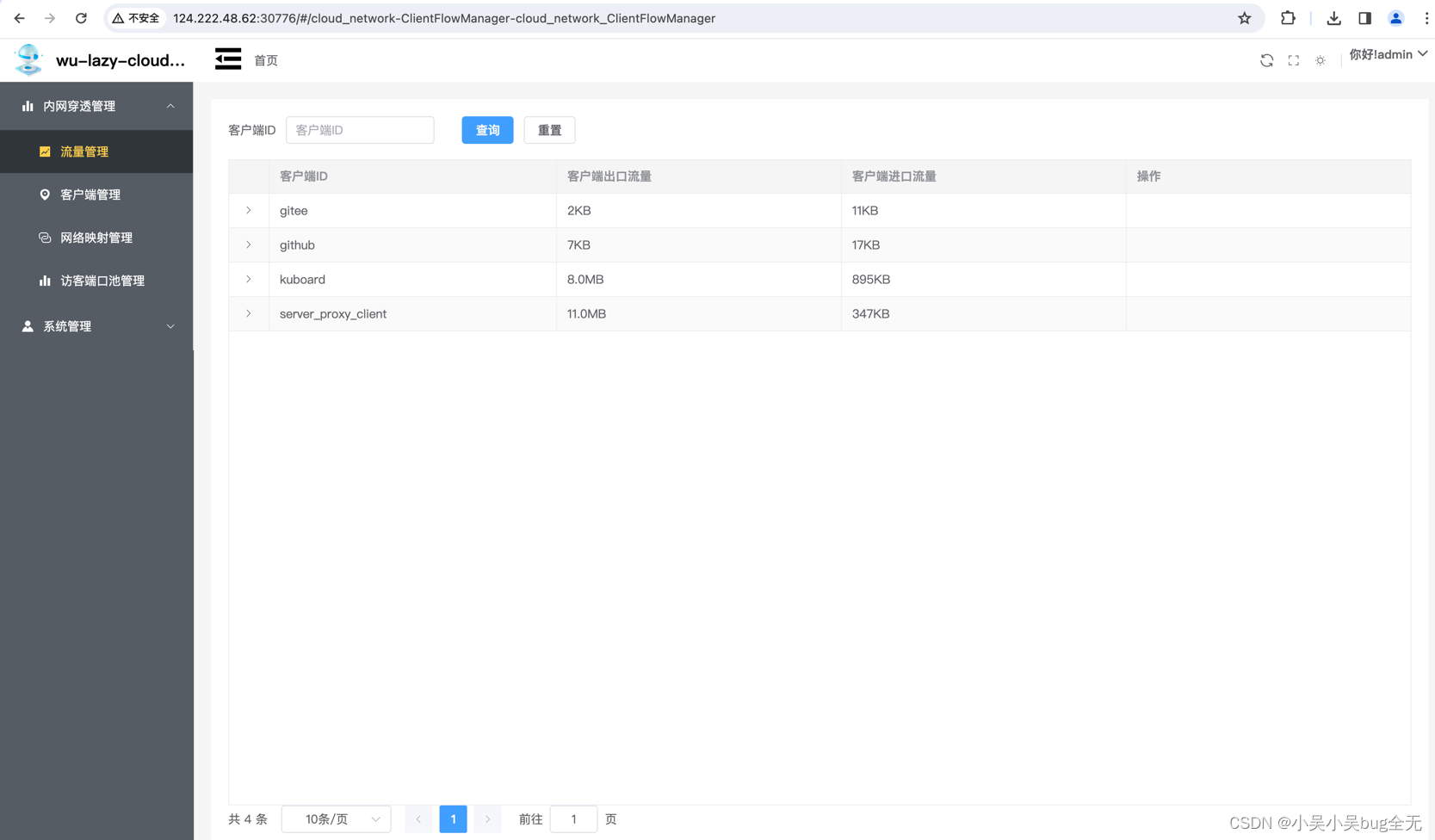
【wu-lazy-cloud-network】Java自动化内网穿透
项目介绍 wu-lazy-cloud-network 是一款基于(wu-framework-parent)孵化出的项目,内部使用Lazy ORM操作数据库,主要功能是网络穿透,对于没有公网IP的服务进行公网IP映射 使用环境JDK17 Spring Boot 3.0.2 功能 1.内网…...
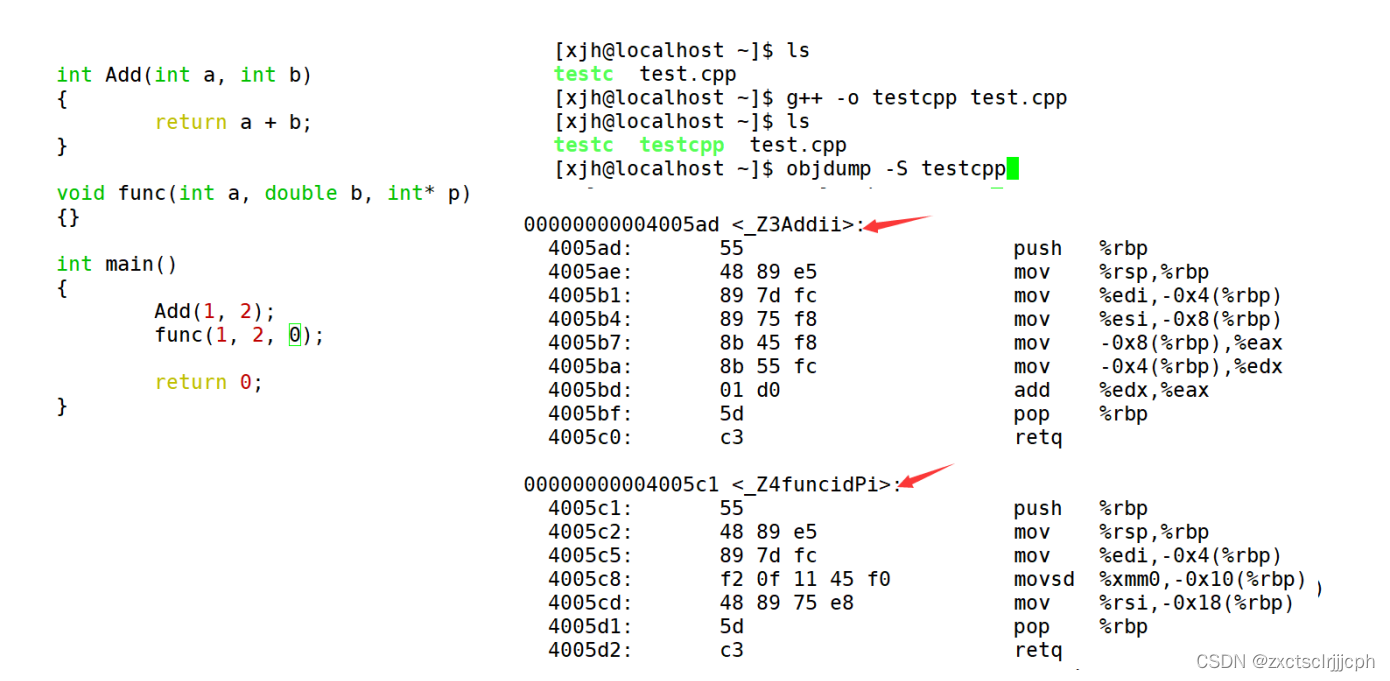
【C++】C++入门(二)
个人主页 : zxctsclrjjjcph 文章封面来自:艺术家–贤海林 如有转载请先通知 文章目录 1. 前言2. 缺省参数2.1 缺省参数概念2.2 缺省参数分类 3. 函数重载3.1 函数重载概念3.2 C支持函数重载的原理--名字修饰(name Mangling) 1. 前言 在前面一篇文章中简…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
