贪心算法篇

“靠漫步,将生趣填饱~”
贪心算法简介?
贪心算法(Greedy Algorithm),也称为贪婪算法,是一种在解决问题时采取贪心策略的方法。其基本原理是很简单的:
“在每个决策点上都选择当下看似最好的选项,而不是寻求全局最优点”。
我们举几个,常使用贪心算法的小例:
找零问题:
此时你的顾客一手掏出50“大米”递给你,一手拿着一瓶快乐水——“nutrition happy line”(you know,这瓶饮料的价格为4)。现如今,这位顾客正一脸疑惑地盯着你的一举一动,因为你接过纸币后,目不转睛地瞅着那数字不小的“大米”愣神。你总会在感到一股苍劲的凉风过后,两眼冒星,腥咸的液体会被你从口中送入食管——你应当马上给他找零了。拉开你正下方,散发着浓烈朽木味儿的抽屉,你从中看到了无数的纸币,其中的面额如下:[20, 10 , 5 ,1]。你需要使用最少的纸币,完成找零工作:
已知,我们要给这位虎背熊腰的壮汉的找零数是:46。又要求我们使用最小的纸币数,所以,我们将两张黄旧的、纸面油印为20的纸币重叠好,再选取面额分别为5和1的纸币,一并夹在手指之间,塞给了这位壮汉。我们的选择为:20 * 2 + 5 * 1 + 1 * 1 = 46。总共需要四张纸币,完成这份找零工作。这便是最少使用纸币的解法。
最小路径和:
这天你命犯桃花,因为本应对你爱答不理、而你却日夜心念的邻家小妹邀请你同她加入到这一场由神秘人创办的乐园探险中。你本以为这仅仅只是一场普通的游乐主题,彼时暗自窃喜,怀揣着想入非非的心思,幻想着邻家小妹把你相拥、同你腻歪的恋爱场景。然而,这场游戏完完全全没有表面看起来那么简单,处处透露着诡异、怪诞,你莫名被卷入到了一场恐怖的布局和惊天的阴谋之中,感受来自黑暗的惊悚:消失的人脸、怪异的乞丐、脱落的车轨以及血腥、压抑的迷宫……
每个格子的数字,代表着探寻这个九宫格格子的时间。你需要花最少的时间,进入到右下角的最后一个格子之中,从恶魔的祭奠仪式拯救邻家小妹……

上述的两个例子,对于第一个例子而言,选择的方案:“尽可能选择较大面额的纸币” ,最终我们可以得到“最优解”。相反,对于第二个例子而言,我们的选择是 “选择花费时间较少的格子”进行探索,然而事实上,得出的并不是最优解。
贪心算法通常会逐步构建问题的解空间,每次尝试将下一个待选元素加入到解集中,直到无法再添加为止。这个过程会使得问题简化为一系列子问题,每个子问题都可以通过同样的贪婪策略来解决,从而逐步接近整体的最优解。
所谓的这些从局部的角度考虑选择的方案,实质上就是“贪心”策略。然而,“贪心”策略也可能是“错误”的方法,让我们得不出最有解。所以,正确的“贪心”策略,是需要进行验证、证明的。
柠檬水找零
(1) 题目解析

(2) 算法原理

class Solution {
public:bool lemonadeChange(vector<int>& bills) {// 记录5$ 10$的个数int five = 0,ten = 0;for(auto& bill:bills){if(bill == 5) five++; // 5$ 直接收下else if(bill == 10){if(five == 0) return false; // 没有5$ 不能找零else five--;ten++; // 收下10$}else{if(five && ten) five--,ten--; // 贪心策略:尽量保留5$else if(five > 2) five -= 3;else return false;}}return true;}
};贪心证明:
贪心只是一种策略,考虑的角度也仅仅是局部的“最优解”,所以,贪心策略也可能是“错误的”
如何确定贪心求得的解就是最优解,还需要进行证明求真。
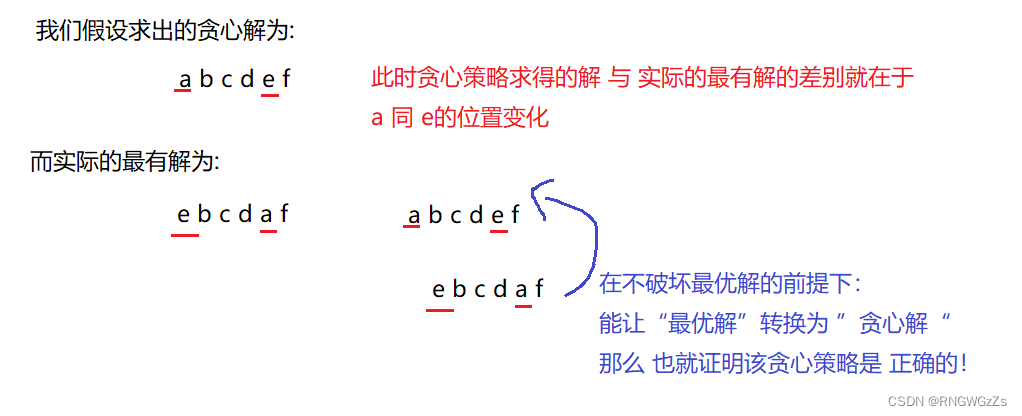
🥃 证明策略1:交换论证

将数组和减半的最少操作次数
(1) 题目解析 
(2) 算法原理

class Solution {
public:int halveArray(vector<int>& nums) {priority_queue<double> pq;double sum = 0;for(auto n:nums){pq.push(n);sum += n; }sum /= 2.0;// 数组减半int count = 0; // 记录操作次数while(sum > 0){double top = pq.top();pq.pop();top /= 2.0;sum -= top;pq.push(top);count++;}return count;}
};贪心证明:
🍷 交换论证法:

最大数
(1) 题目解析

(2) 算法原理

class Solution {
public:string largestNumber(vector<int>& nums) {vector<string> strs;for(auto x:nums) strs.push_back(to_string(x));sort(strs.begin(),strs.end(),[](const string& s1,const string& s2){return s1 + s2 > s2 + s1;});// 提取结果string res;for(auto& s:strs) res += s;// 处理前置0if(res[0] == '0') return "0";return res;}
};贪心证明:
似乎,没有看到本题的贪心策略呢? 贪心在何处?

摆动序列
(1) 题目解析

(2) 算法原理 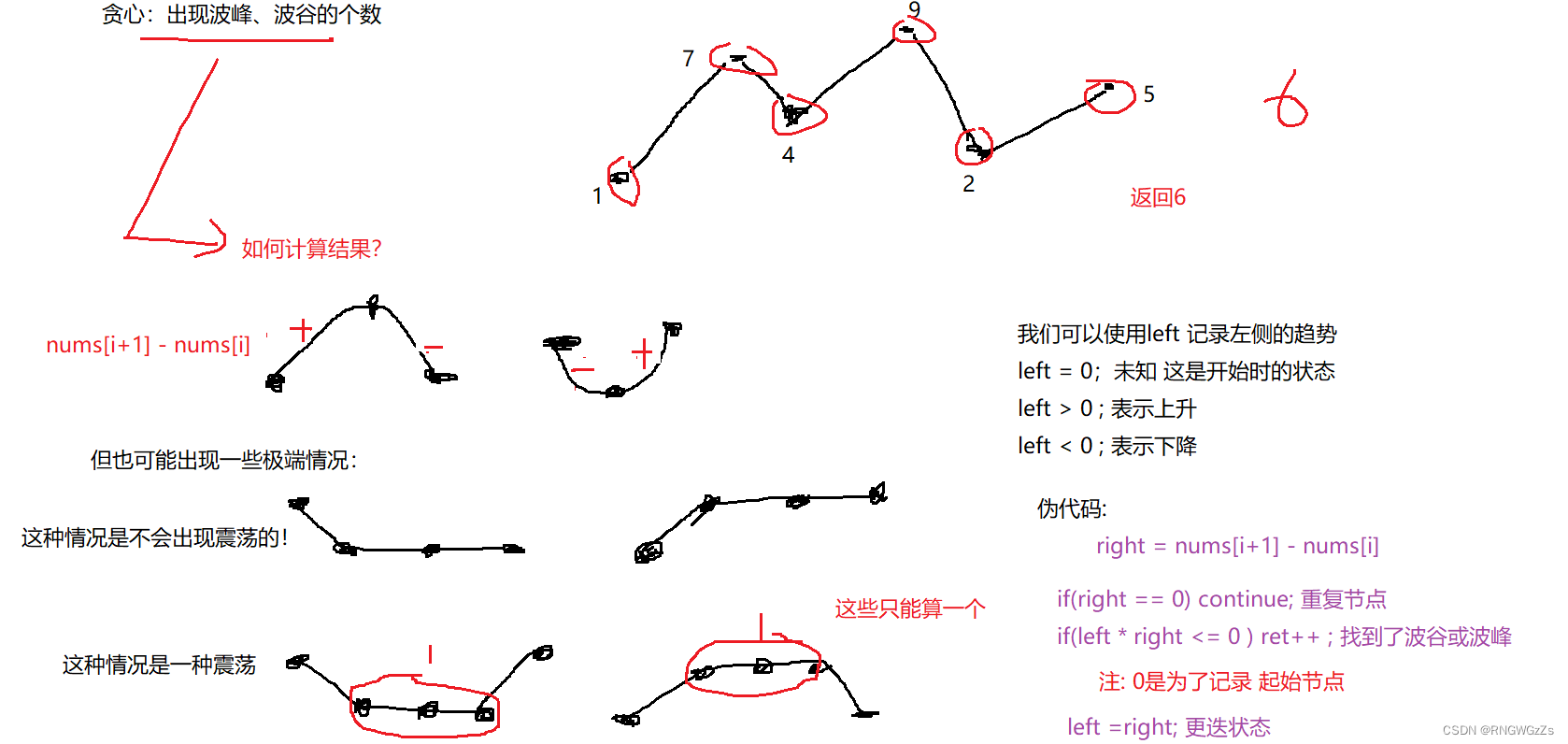
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size() < 2) return nums.size();int ret = 0,left = 0;for(int i=0;i < nums.size() - 1;++i){int right = nums[i+1] - nums[i];if(right == 0) continue;if(left * right <=0) ret++;left = right;}// +1表示末尾节点return ret + 1;}
};贪心证明:
🥣 反证法:

本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~

相关文章:

贪心算法篇
“靠漫步,将生趣填饱~” 贪心算法简介? 贪心算法(Greedy Algorithm),也称为贪婪算法,是一种在解决问题时采取贪心策略的方法。其基本原理是很简单的: “在每个决策点上都选择当下看似最好的选项…...

springboot/ssm大学生就业服务平台就业招聘宣传管理系统Java系统
springboot(ssm大学生就业服务平台 就业招聘宣传管理系统Java系统 开发语言:Java 框架:springboot(可改ssm) vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql…...

上下固定中间自适应布局
实现上下固定中间自适应布局 1.通过position:absolute实现 定义如下结构 <body> <div class"container"> <div class"top"></div> <div class"center"></div> <div class"bottom&…...
3分钟部署完成Docker Registry及可视化管理工具Docker-UI
安装docker-registry 由于镜像文件会非常占用空间,因此需要选择一个磁盘充裕的位置来存放镜像数据。 这里设置为:-v /data/registry:/var/lib/registry,其中/data/registry是宿主机存放数据的位置。 docker run -d -p 5000:5000 --restart…...
【npm】修改npm全局安装包的位置路径
问题 全局安装的默认安装路径为:C:\Users\admin\AppData\Roaming\npm,缓存路径为:C:\Users\admin\AppData\Roaming\npm_cache(其中admin为自己的用户名)。 由于默认的安装路径在C盘,太浪费C盘内存啦&#…...

数据库切片大对决:ShardingSphere与Mycat技术解析
欢迎来到我的博客,代码的世界里,每一行都是一个故事 数据库切片大对决:ShardingSphere与Mycat技术解析 前言ShardingSphere与Mycat简介工作原理对比功能特性对比 前言 在数据库的舞台上,有两位颇受欢迎的明星,它们分别…...
macbook电脑如何永久删除app软件?
在使用MacBook的过程中,我们经常会下载各种App来满足日常的工作和娱乐需求。然而,随着时间的积累,这些App不仅占据了宝贵的硬盘空间,还可能拖慢电脑的运行速度。那么,如何有效地管理和删除这些不再需要的App呢…...
)
安卓——计算器应用(Java)
步骤 1: 设置Android Studio项目 创建一个新的Android项目,选择Java作为编程语言。 步骤 2: 设计用户界面 打开activity_main.xml文件,在res/layout目录下,设计你的计算器用户界面。这个例子使用了LinearLayout来排列两个EditText输入框和…...

【笔记】Helm-5 Chart模板指南-8 命名模板
命名模板 此时需要越过模板,开始创建其他内容了。该部分我们会看到如何在一个文件中定义 命名模板,并在其他地方使用。命名模板(有时称作一个部分或一个子模板)仅仅是在文件内部定义的模板,并使用了一个名字。有两种创…...
Github 2024-02-08 开源项目日报 Top9
根据Github Trendings的统计,今日(2024-02-08统计)共有9个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Ruby项目1HTML项目1Python项目1Scala项目1PLpgSQL项目1Rust项目1NASL项目1C项目1TypeScript项目1非开发语言项目…...

c语言贪食蛇游戏
演示视频 目录 一.概述 二.游戏开始前 修改控制台程序标题和大小 Win32 API GetStdHandle函数 GetConsoleCursorInfo函数和SetConsoleCursorInfo函数 SetConsoleCursorPosition函数 游戏开篇界面处理 创建地图 蛇身节点以及食物节点初始化 蛇身的初始化 整体蛇节点…...

国际物流数字化运输方式选择指南 | 箱讯科技
国际物流涉及多种运输方式,每种方式都有其独特的优势和适用场景。选择合适的运输方式对于确保货物安全、及时到达目的地并控制成本至关重要。以下是对六种主要国际运输方式的简要介绍和选择建议: 国际快递:适用于小件、高价值或急需的货物。…...

FPS游戏框架漫谈第二十天
今天我们聊的话题是: 《吃鸡中武器护甲逻辑》 当我们接到一个需求就是给我们游戏中的特定的模式指定的武器支持加护甲的功能 那么这个流程是什么样的呢? 第一步一般这个新增护甲的配置属性肯定是加载武器的Config json文件里面的呢,并且是支持…...
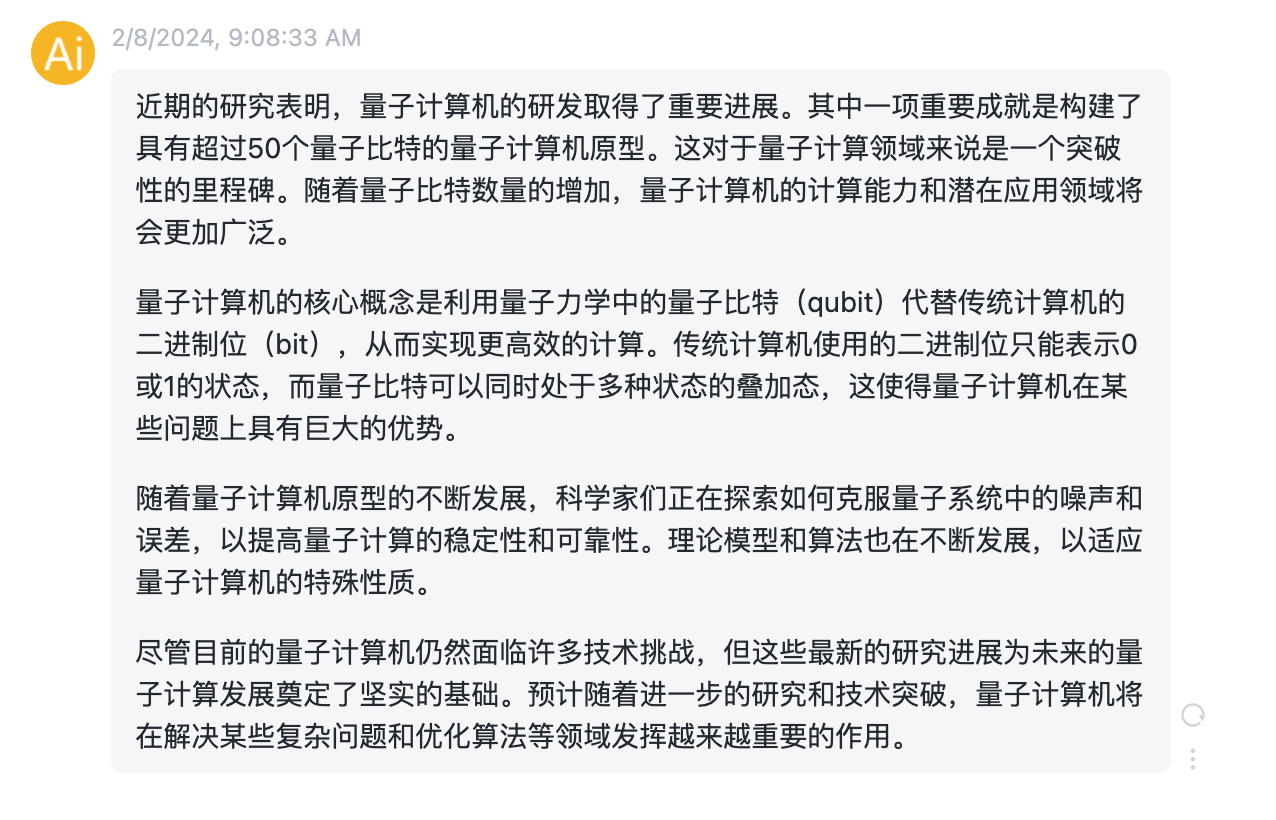
ChatGPT高效提问—prompt常见用法(续篇四)
ChatGPT高效提问—prompt常见用法(续篇四) 1.1 知识生成 知识生成是指使用自然语言处理技术,通过ChatGPT等AI模型生成与特定主题相关的知识、文本或回答。在知识生成过程中,模型接收prompt输入的问题、指令或上下文信息&…...
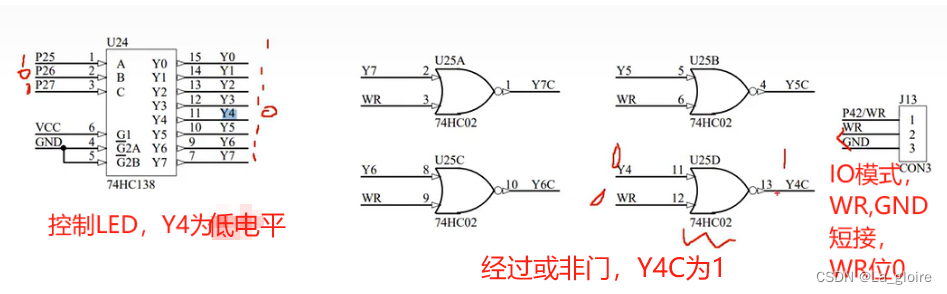
【蓝桥杯单片机记录】IO基础与LED控制
目录 一、IO基础 1.1 IAP15F2K61S2芯片原理图 1.2不同工作模式 二、新建工程的一些补充 2.1 keil中没有IAP15F2K61S2的头文件 解决:在isp软件中找到如下编辑 2.2keil中的芯片选择 2.3推荐字体 三、sbit关键字 四、LED控制 4.1原理图 4.2不能直接通过IO…...

java 回答问题
1. How do you create a variable with the numeric value 5? int x 5; 2. The value of a string variable can be surrounded by single quotes. False 3. Which method can be used to return a string in upper case letters? toUpperCase()...
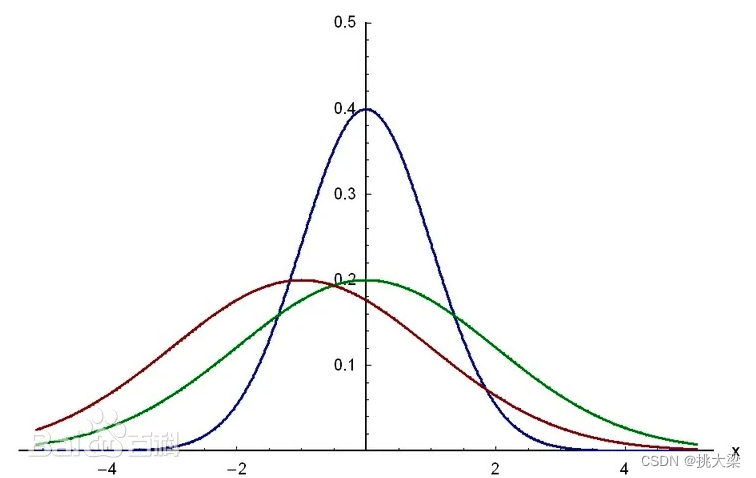
彻底学会系列:一、机器学习之线性回归(一)
1.基本概念(basic concept) 线性回归: 有监督学习的一种算法。主要关注多个因变量和一个目标变量之间的关系。 因变量: 影响目标变量的因素: X 1 , X 2 . . . X_1, X_2... X1,X2... ,连续值或离散值。 目标变量: …...

FPGA:我的零基础学习路线(2022秋招已上岸)持续更新中~
可内推简历,丝我即可 前言 初次接触FPGA是在2022年3月左右,正处在研二下学期,面临着暑假找工作,周围的同学大多选择了互联网,出于对互联网的裁员形势下,我选择了FPGA,对于硬件基础知识我几乎是…...

阿里云游戏服务器多少钱一个月?
阿里云游戏服务器租用价格表:4核16G服务器26元1个月、146元半年,游戏专业服务器8核32G配置90元一个月、271元3个月,阿里云服务器网aliyunfuwuqi.com分享阿里云游戏专用服务器详细配置和精准报价: 阿里云游戏服务器租用价格表 阿…...
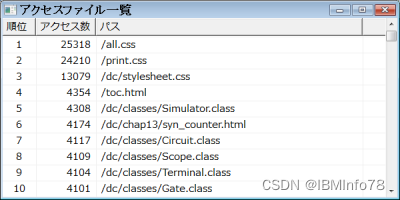
Win32 SDK Gui编程系列之--ListView自绘OwnerDraw(续)
通过所有者绘制的列表视图(2) 所有者绘制列表视图的基础已在前一页中说明。本页将展示如何在所有者绘制列表视图中显示数据库表数据。 1、访问日志 正如在另一个页面中所述,本网站的访问日志目前是通过SQLite3数据库管理的。 以下是上述程序执行的结果。为…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...
