2024.1.26力扣每日一题——边权重均等查询
2024.1.26
- 题目来源
- 我的题解
- 方法一 使用dfs对每一组查询都求最近公共祖先(会超时,通不过)
- 方法二 不需要构建图,直接在原始数组上进行求最大公共祖先的操作。
题目来源
力扣每日一题;题序:2846
我的题解
方法一 使用dfs对每一组查询都求最近公共祖先(会超时,通不过)
使用dfs对每一组查询都去找最近公共祖先,并在这个过程中统计边的权重,最后通过TreeMap计算出边权重集合中元素重复的最大次数,贪心策略可知,结果为:查询路径上总共的边-最大次数。
时间复杂度:O( n 2 n^2 n2)
空间复杂度:O( m × n m\times n m×n)
List<Integer> list;public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {Map<Integer,Integer>[] graph=createGraph(n,edges);int qn=queries.length;int[] res=new int[qn];for(int i=0;i<qn;i++){int from=queries[i][0];int to=queries[i][1];if(from==to)continue;list=new ArrayList<>();boolean[] visited=new boolean[n];dfs(graph,from,to,visited,new ArrayList<>());res[i]=needChange(list);}return res;}public int needChange(List<Integer> l){TreeMap<Integer, Long> frequencyMap = new TreeMap<>(l.stream().collect(Collectors.groupingBy(Function.identity(), Collectors.counting())));TreeMap<Integer, Long> frequencySortMap=new TreeMap<>(Comparator.comparing(frequencyMap::get));frequencySortMap.putAll(frequencyMap);return l.size()-Integer.parseInt(frequencySortMap.get(frequencySortMap.lastKey()).toString());}public Map<Integer,Integer>[] createGraph(int n,int[][] edges){Map<Integer,Integer>[] graph=new HashMap[n];for(int i=0;i<n;i++)graph[i]=new HashMap<>();for(int[] e:edges){int from =e[0];int to=e[1];int val=e[2];graph[from].put(to,val);graph[to].put(from,val);}return graph;}public void dfs(Map<Integer,Integer>[] graph,int from,int to,boolean[] visited,List<Integer> path){if(from==to){list=new ArrayList(path);return ;}visited[from]=true;for(int next:graph[from].keySet()){if(!visited[next]){path.add(graph[from].get(next));dfs(graph,next,to,visited,path);path.remove(path.size()-1);}}visited[from]=false;}
方法二 不需要构建图,直接在原始数组上进行求最大公共祖先的操作。
参考:官方题解
以节点 0 为根节点,使用数组 count[i]记录节点 i到根节点 0 的路径上边权重的数量,即 count[i][j] 表示节点 i到根节点 0 的路径上权重为 j的边数量。对于查询 queries[i]=[ a i a_i ai, b i b_i bi],记节点 l c a i lca_i lcai为节点 a i a_i ai与 b i b_i bi的最近公共祖先,那么从节点 a i a_i ai到节点 b i b_i bi的路径上,权重为 j 的边数量 t j t_j tj的计算如下:
t j = count [ a i ] [ j ] + count [ b i ] [ j ] − 2 × count [ lca i ] [ j ] t_j = \textit{count}[a_i][j] + \textit{count}[b_i][j] - 2 \times \textit{count}[\textit{lca}_i][j] tj=count[ai][j]+count[bi][j]−2×count[lcai][j]
为了让节点 a i a_i ai到节点 b i b_i bi路径上每条边的权重都相等,贪心地将路径上所有的边都更改为边数量最多的权重即可,即从节点 a i a_i ai到节点 b i b_i bi路径上每条边的权重都相等所需的最小操作次数 r e s i res_i resi的计算如下: res i = ∑ j = 1 W t j − max 1 ≤ j ≤ W t j \textit{res}_i = \sum_{j=1}^{W}t_j - \max_{1 \le j \le W}t_j resi=∑j=1Wtj−max1≤j≤Wtj
其中 W=26W = 26W=26 表示权重的最大值。
时间复杂度:O((m+n)×W+m×logn),其中 n 是节点数目,m 是查询数目,W 是权重的可能取值数目。
空间复杂度:O(n×W+m)
class Solution {static final int W = 26;public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {int m = queries.length;Map<Integer, Integer>[] neighbors = new Map[n];for (int i = 0; i < n; i++) {neighbors[i] = new HashMap<Integer, Integer>();}for (int[] edge : edges) {neighbors[edge[0]].put(edge[1], edge[2]);neighbors[edge[1]].put(edge[0], edge[2]);}List<int[]>[] queryArr = new List[n];for (int i = 0; i < n; i++) {queryArr[i] = new ArrayList<int[]>();}for (int i = 0; i < m; i++) {queryArr[queries[i][0]].add(new int[]{queries[i][1], i});queryArr[queries[i][1]].add(new int[]{queries[i][0], i});}int[][] count = new int[n][W + 1];boolean[] visited = new boolean[n];int[] uf = new int[n];int[] lca = new int[m];tarjan(0, -1, neighbors, queryArr, count, visited, uf, lca);int[] res = new int[m];for (int i = 0; i < m; i++) {int totalCount = 0, maxCount = 0;for (int j = 1; j <= W; j++) {int t = count[queries[i][0]][j] + count[queries[i][1]][j] - 2 * count[lca[i]][j];maxCount = Math.max(maxCount, t);totalCount += t;}res[i] = totalCount - maxCount;}return res;}public void tarjan(int node, int parent, Map<Integer, Integer>[] neighbors, List<int[]>[] queryArr, int[][] count, boolean[] visited, int[] uf, int[] lca) {if (parent != -1) {System.arraycopy(count[parent], 0, count[node], 0, W + 1);count[node][neighbors[node].get(parent)]++;}uf[node] = node;for (int child : neighbors[node].keySet()) {if (child == parent) {continue;}tarjan(child, node, neighbors, queryArr, count, visited, uf, lca);uf[child] = node;}for (int[] pair : queryArr[node]) {int node1 = pair[0], index = pair[1];if (node != node1 && !visited[node1]) {continue;}lca[index] = find(uf, node1);}visited[node] = true;}public int find(int[] uf, int i) {if (uf[i] == i) {return i;}uf[i] = find(uf, uf[i]);return uf[i];}
}
困难题果然不是我会做的,做做搬运工得了
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

2024.1.26力扣每日一题——边权重均等查询
2024.1.26 题目来源我的题解方法一 使用dfs对每一组查询都求最近公共祖先(会超时,通不过)方法二 不需要构建图,直接在原始数组上进行求最大公共祖先的操作。 题目来源 力扣每日一题;题序:2846 我的题解 …...

C语言操作符超详细总结
文章目录 1. 操作符的分类2. 二进制和进制转换2.1 2进制转10进制2.1.1 10进制转2进制数字 2.2 2进制转8进制和16进制2.2.1 2进制转8进制2.2.2 2进制转16进制 3. 原码、反码、补码4.移位操作符4.1 左移操作符4.2 右移操作符 5. 位操作符:&、|、^、~6. 逗号表达式…...
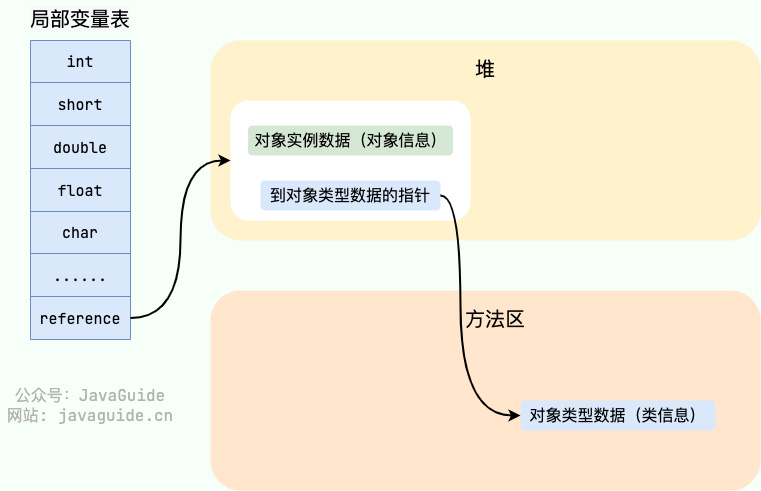
【Java八股面试系列】JVM-内存区域
目录 Java内存区域 运行时数据区域 线程独享区域 程序计数器 Java 虚拟机栈 StackFlowError&OOM 本地方法栈 线程共享区域 堆 GCR-分代回收算法 字符串常量池 方法区 运行时常量池 HotSpot 虚拟机对象探秘 对象的创建 对象的内存布局 句柄 Java内存区域 运…...

计划任务功能优化,应用商店上架软件超过100款,1Panel开源面板v1.9.6发布
2024年2月7日,现代化、开源的Linux服务器运维管理面板1Panel正式发布v1.9.6版本。 在v1.9.5和v1.9.6这两个小版本中,1Panel针对计划任务等功能进行了多项优化和Bug修复。此外,1Panel应用商店新增了3款应用,上架精选软件应用超过1…...
2023省赛真题3:收集帛书碎片)
蓝桥杯(Web大学组)2023省赛真题3:收集帛书碎片
需要实现: 1.将二维数组转为一维数组; 2.数组去重 一、将二维数组转为一维数组: 二、数组去重: function collectPuzzle(...puzzles) {// console.log(puzzles);// console.log(...puzzles);// TODO:在这里写入具体的实现逻辑/…...
使用QT编写一个简单QQ登录界面
widget.cpp #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//设置窗口标题this->setWindowTitle("QQ");//设置窗口图标this->setWindowIcon(…...

TryHackMe-Net Sec Challenge练习
本文相关的TryHackMe实验房间链接:TryHackMe | Why Subscribe nmap nmap -T5 -p- 10.10.90.32 -T5 扫描速度 -p- 全端口扫描 答题: 这题叫我们找藏在http服务下的flag,根据上面扫出来的端口,所以我们开始搞80 这里简单介绍一下…...

面试 JavaScript 框架八股文十问十答第五期
面试 JavaScript 框架八股文十问十答第五期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)常见的位运算符有…...

[职场] 如何通过运营面试_1 #笔记#媒体#经验分享
如何通过运营面试 盈利是公司的事情,而用户就是你运营的事情。你需要彻底建立一个庞大而有效的用户群,这样才能让你们的公司想盈利就盈利,想战略就战略,想融资就融资。 一般从事运营的人有着强大的自信心,后台数据分析…...
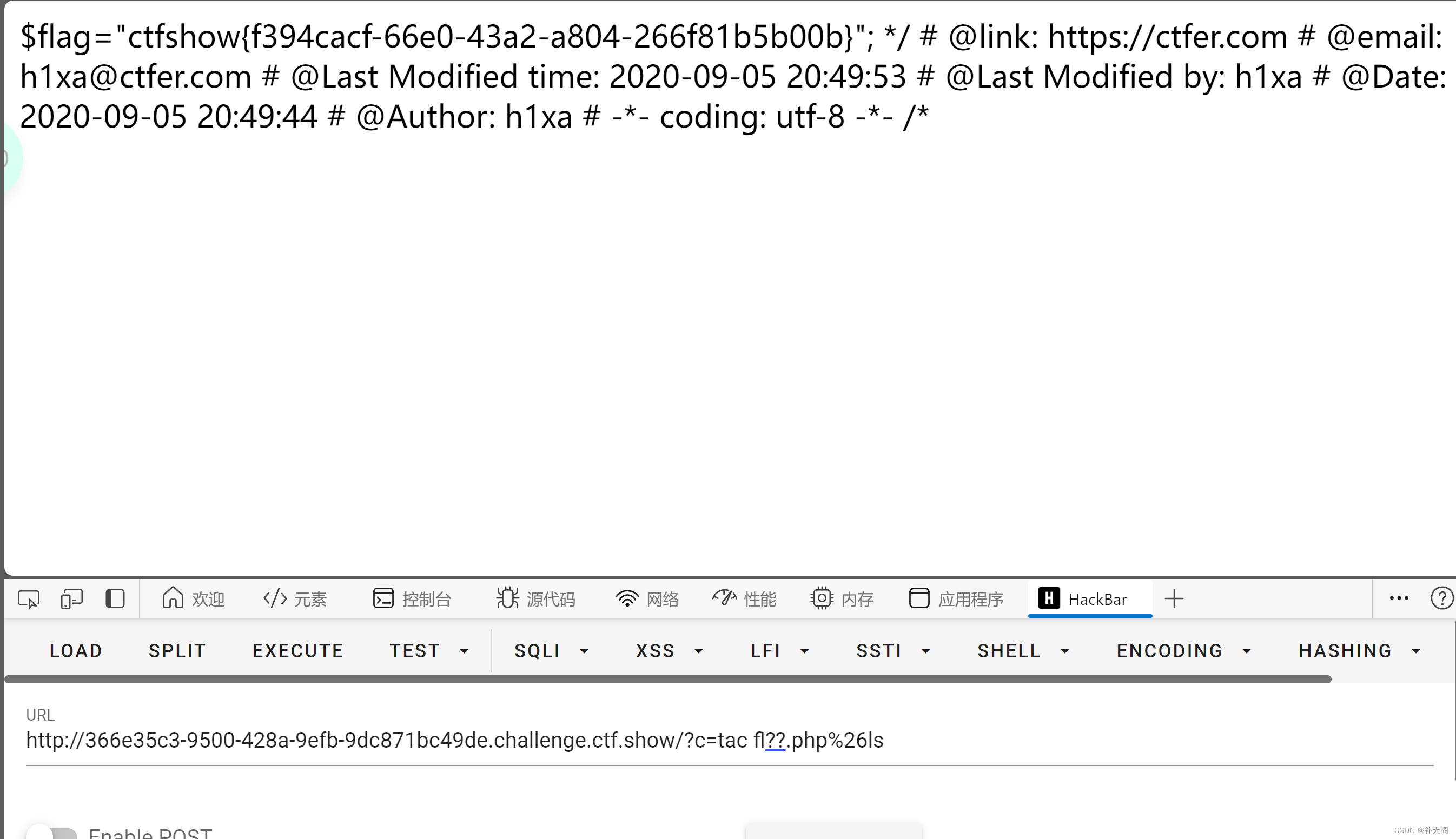
CTFshow web(命令执行 41-44)
web41 <?php /* # -*- coding: utf-8 -*- # Author: 羽 # Date: 2020-09-05 20:31:22 # Last Modified by: h1xa # Last Modified time: 2020-09-05 22:40:07 # email: 1341963450qq.com # link: https://ctf.show */ if(isset($_POST[c])){ $c $_POST[c]; if(!p…...

XML介绍和基本语法
XML简介 XML(eXtensible Markup Language,可扩展标记语言)是一种用于标记电子文件使其具有结构性的标记语言。它允许用户定义自己的标记元素,使得信息的共享和数据的存储更加便捷和通用。XML广泛应用于Web开发、配置文件、数据交…...
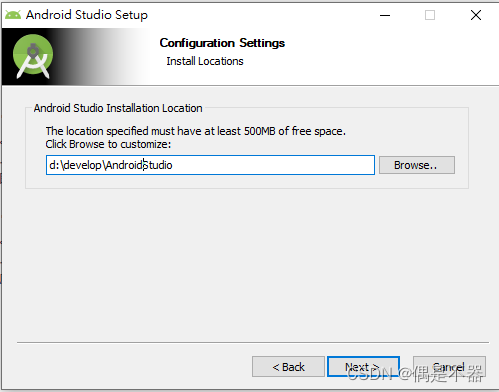
Android:Android Studio安装及环境配置
1开发环境搭建 Android开发需要使用java的jdk环境,所以需要下载JAVA JDK。 1.1安装配置JAVA JDK Java的JDK下载: https://www.oracle.com/technetwork/java/javase/downloads/index.html 配置java的环境变量: JAVA_HOME:java安装路径。 新增环境变量CLASSPATH 在Path环境…...

力扣刷题之旅:进阶篇(三)
力扣(LeetCode)是一个在线编程平台,主要用于帮助程序员提升算法和数据结构方面的能力。以下是一些力扣上的入门题目,以及它们的解题代码。 --点击进入刷题地址 一、动态规划(DP) 首先,让我们来…...

代码随想录 Leetcode55. 跳跃游戏
题目: 代码(首刷自解 2024年2月9日): class Solution { public:bool canJump(vector<int>& nums) {int noz 0;for (int i nums.size() - 2; i > 0; --i) {if (nums[i] 0) {noz;continue;} else {if (nums[i] > noz) noz …...

Go Context -- 管理请求的上下文信息
在Go语言中,管理请求的上下文信息对于构建可靠的并发程序至关重要。context 包为我们提供了一种优雅的方式来传递请求的取消信号、超时信息和请求范围的值。接下来将深入探讨Go中的 context 包,包括其基本概念、用法、实际应用场景和最佳实践,…...
springboot170图书电子商务网站的设计与实现
简介 【毕设源码推荐 javaweb 项目】基于springbootvue 的 适用于计算机类毕业设计,课程设计参考与学习用途。仅供学习参考, 不得用于商业或者非法用途,否则,一切后果请用户自负。 看运行截图看 第五章 第四章 获取资料方式 **项…...
适配器模式)
设计模式(结构型模式)适配器模式
目录 一、简介二、使用2.1、目标接口2.2、被适配者2.3、适配器2.4、使用 一、简介 适配器模式是一种结构型设计模式,允许将一个类的接口转换成客户端所期望的另一个接口,使得原本由于接口不兼容而不能一起工作的类能够协同工作。适配器模式通常用于连接两…...

计算机网络基本知识(二)
文章目录 概要分层为什么分层怎么分层?1.实体2.协议3.服务 分层基本原则正式认识分层详细例子解释 总结 概要 分层知识:概念理解 分层 为什么分层 大致以上五点 为了解决上面的问题(复杂) 大问题划分为小问题 怎么分层&#…...

158基于matlab的用于分析弧齿锥齿轮啮合轨迹的程序
基于matlab的用于分析弧齿锥齿轮啮合轨迹的程序,输出齿轮啮合轨迹及传递误差。程序已调通,可直接运行。 158 matlab 弧齿锥齿轮啮合轨迹 传递误差 (xiaohongshu.com)...

C#中的浅度和深度复制(C#如何复制一个对象)
文章目录 浅度和深度复制浅度复制深度复制如何选择 浅度和深度复制 在C#中,浅度复制(Shallow Copy)和深度复制(Deep Copy)是两种不同的对象复制方式,满足不同的应用场景需求,它们主要区别在于处…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
