python巧用定理判断素数
目录
判断一个数n是否是素数
求一个数的素因数个数
求大于等于指定数的最小素数
在数论中有三个非常重要的关于素数的定理
1、任何数都可以表示成若干个素数的乘积
2、任意数的素因子一个大于根号n的自然数,另一个与其对应的因子则必小于根号n。
3、除了2和3以外的所有素数都是6k±1型(k=1、2、3、...),这里要反过来是不成立的,也就是说6k±1型的不一定都是素数,例如35是6k-1型,但它不是素数
判断一个数n是否是素数
方法1:遍历从2到n-1的所有因子,时间复杂度
def is_prime(n):if n < 2: # 小于2的肯定不是素数return 0for i in range(2, n):if n % i == 0: #如果存在2到n的因子,则不是素数return 0return 1 #如果2到n遍历完后都没有,则是素数方法2:使用性质2,我们其实可以只遍历从2到根号n,此时时间复杂度降为
def is_prime(n):if n < 2: # 小于2的肯定不是素数return 0for i in range(2, int(n**0.5)+1): #这里int会向下取整,所以加1消除误差if n % i == 0: return 0return 1 方法3:使用性质2和性质3,从2到根号n,然后每隔6个数遍历,此时时间复杂度降为
def is_prime(n):if n < 2: return 0if n <= 3: # 2或3肯定是素数return 1if n % 2 == 0 or n % 3 == 0: # 如果能整除2或3,则不是素数return 0for i in range(5, int(n ** 0.5) + 1, 6):#从5开始,步长为6if n % i == 0 or n % (i + 2) == 0: # i表示6k-1,i+2表示6k+1return 0return 1
求一个数的素因数个数
根据定理1,任意数都可以表示为若干个素数的乘积,写一个程序,要求计算一个数的素因子个数
题目链接
https://www.lanqiao.cn/problems/2155/learning/?page=1&first_category_id=1&sort=students_count&category_id=3&name=%E8%B4%A8%E5%9B%A0%E6%95%B0
ans = 0
n = int(input())
# 2和3单独讨论
for i in [2, 3]:if n % i == 0: # 如果可以整除i,即含有素因子ians = ans + 1 # 计数加1while n % i == 0: # 将n一直除以i,直到n中没有因子in = n // ifor i in range(5, int(n ** 0.5) + 1, 6): for j in [i, i + 2]: # j分别表示6k-1和6k+1# 以下过程与上面同理if n % j == 0:ans = ans + 1while n % j == 0:n = n // jif n != 1: # 如果最后除出来结果不是1,说明还剩个素因数,还需要再加1ans = ans + 1print(ans)
输入396,结果为3,因为396有2、3、11三个素因子

求大于等于指定数的最小素数
def is_prime(n):if n < 2:return 0if n <= 3:return 1if n % 2 == 0 or n % 3 == 0:return 0for i in range(5, int(n ** 0.5) + 1, 6):if n % i == 0 or n % (i + 2) == 0:return 0return 1n = int(input())if is_prime(n): # 如果是素数则直接输出print(n)
else:for j in range(1, 7): # 根据性质,最多隔6位肯定会有素数,所以一直给n加1,直到n是素数则输出n = n + 1if is_prime(n):print(n)break输入17

输入35

相关文章:

python巧用定理判断素数
目录 判断一个数n是否是素数 求一个数的素因数个数 求大于等于指定数的最小素数 在数论中有三个非常重要的关于素数的定理 1、任何数都可以表示成若干个素数的乘积 2、任意数的素因子一个大于根号n的自然数,另一个与其对应的因子则必小于根号n。 3、除了2和3以…...

2023年总结
人们总说时间会改变一切,但事实上你得自己来。 今年开始给自己的时间读书、工作、生活都加上一个2.0的release版本号,相比过去的一年还是有很多进步的。 就跟git commit一样,一步一步提交优化,年底了发个版本。用李笑来的话说&am…...
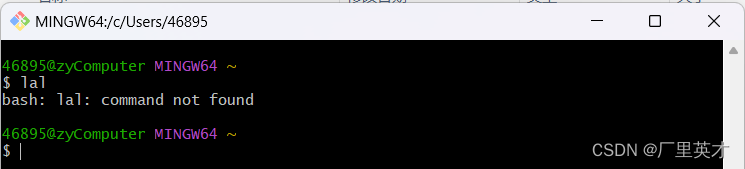
Git中为常用指令配置别名
目录 1 前言 2 具体操作 2.1 创建.bashrc文件 2.2 添加指令 2.3 使其生效 2.4 测试 1 前言 在Git中有一些常用指令比较长,当我们直接输入,不仅费时费力,还容易出错。这时候,如果能给其取个简短的别名,那么事情就…...

STM32内部Flash
目录 一、内部Flash简介 二、内部Flash构成 1. 主存储器 2. 系统存储区 3. 选项字节 三、内部Flash写入过程 1. 解锁 2. 页擦除 3. 写入数据 四、工程空间分布 某工程的ROM存储器分布映像: 1. 程序ROM的加载与执行空间 2. ROM空间分布表 一、内部Flash…...

html5 audio video
DOMException: play() failed because the user didn‘t interact with the document first.-CSDN博客 不可用: 可用: Google Chrome Close AutoUpdate-CSDN博客...
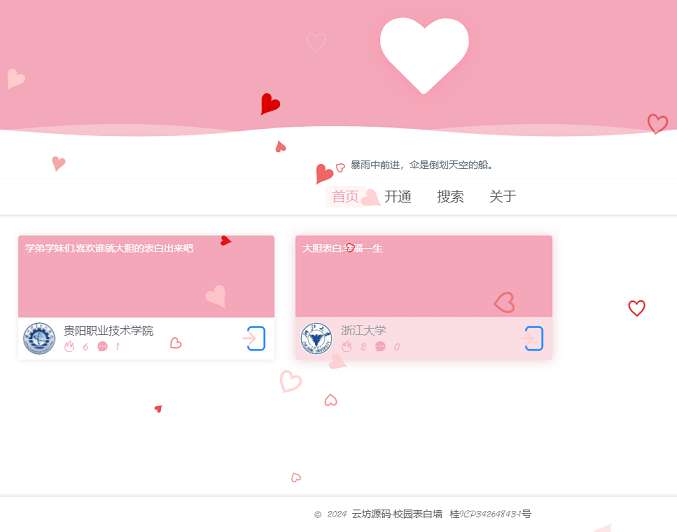
LoveWall v2.0Pro社区型校园表白墙源码
校园表白墙,一个接近于社区类型的表白墙,LoveWall。 源码特色; 点赞, 发评论, 发弹幕, 多校区, 分享页, 涉及违禁物等名词进行检测! 安装教程: 环境要求;…...
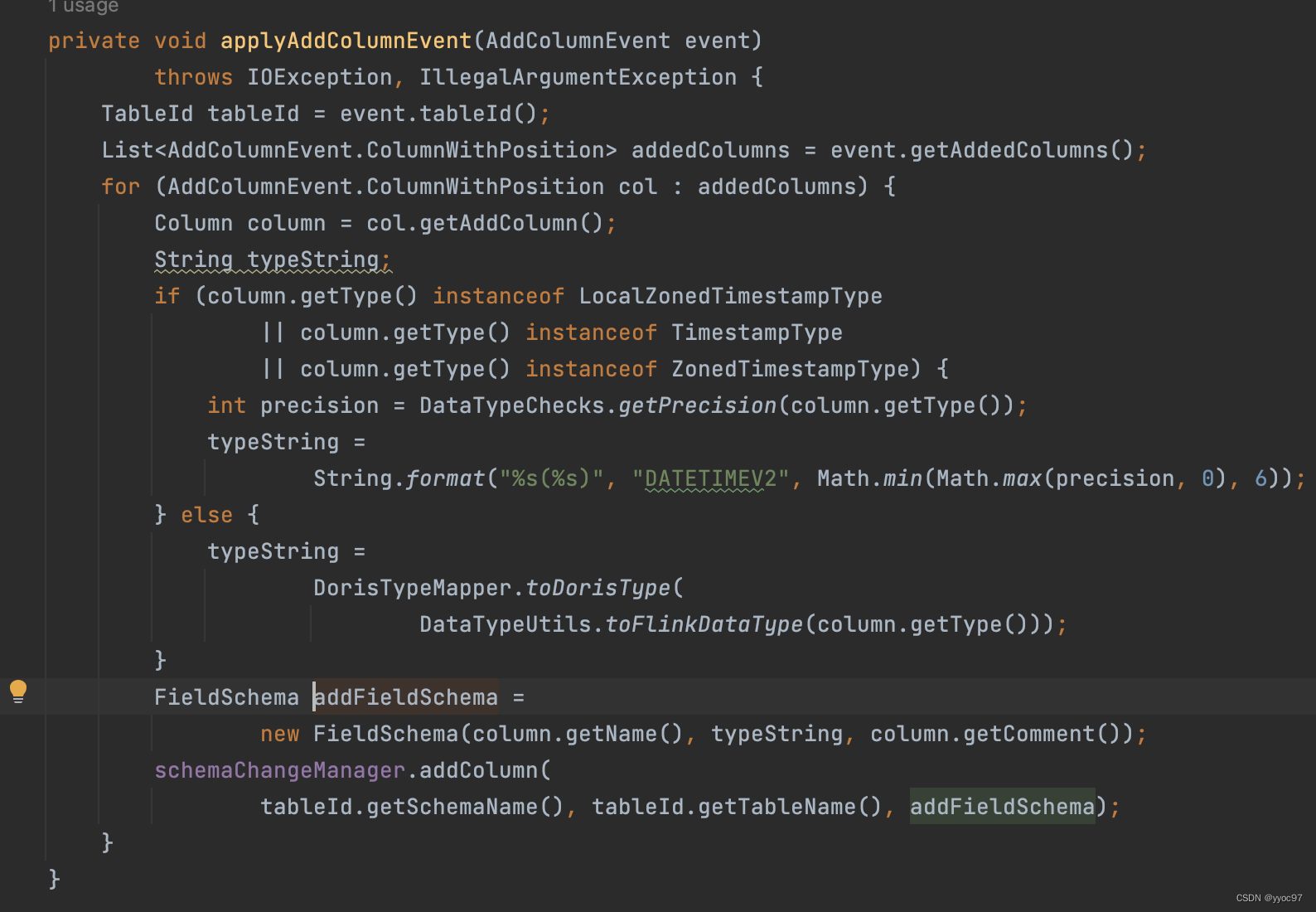
Flink cdc3.0动态变更表结构——源码解析
文章目录 前言源码解析1. 接收schema变更事件2. 发起schema变更请求3. schema变更请求具体处理4. 广播刷新事件并阻塞5. 处理FlushEvent6. 修改sink端schema 结尾 前言 上一篇Flink cdc3.0同步实例 介绍了最新的一些功能和问题,本篇来看下新功能之一的动态变更表结…...

WWW 2024 | 时间序列(Time Series)和时空数据(Spatial-Temporal)论文总结
WWW 2024已经放榜,本次会议共提交了2008篇文章,research tracks共录用约400多篇论文,录用率为20.2%。本次会议将于2024年5月13日-17日在新加坡举办。 本文总结了WWW 2024有关时间序列(Time Series)和时空数据…...

代码随想录算法——数组
目录 1、二分查找法 2、移除元素 3、有序数组的平方 4、长度最小的子数组 5、螺旋矩阵II 1、二分查找法 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在…...
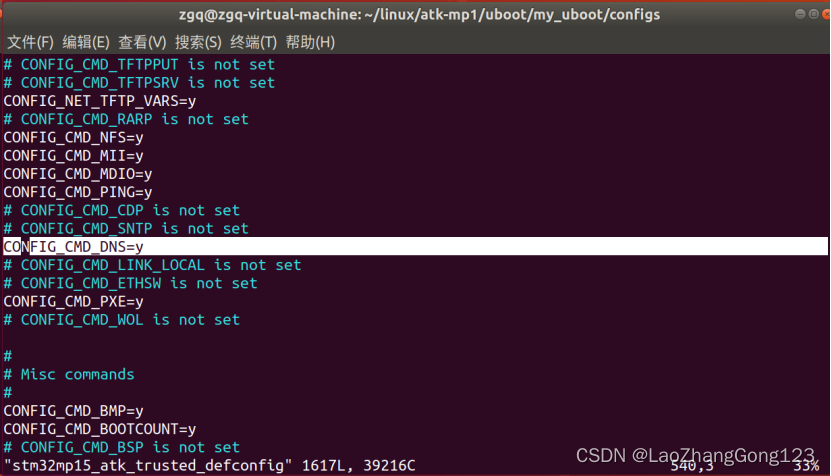
Linux第45步_通过搭建“DNS服务器”学习图形化配置工具
学习的意义:通过搭建“DNS服务器”,来学习“图形化配置工具”。“DNS服务器”,我们用不到,但为后期移植linux系统服务,因为在移植系统时,需要用到这个“图形化配置工具”。 1、“menuconfig图形化配置工具…...

【Linux取经路】探寻shell的实现原理
文章目录 一、打印命令行提示符二、读取键盘输入的指令三、指令切割四、普通命令的执行五、内建指令执行5.1 cd指令5.2 export指令5.3 echo指令 六、结语 一、打印命令行提示符 const char* getusername() // 获取用户名 {return getenv("USER"); }const char* geth…...
【MATLAB】使用随机森林在回归预测任务中进行特征选择(深度学习的数据集处理)
1.随机森林在神经网络的应用 当使用随机森林进行特征选择时,算法能够为每个特征提供一个重要性得分,从而帮助识别对目标变量预测最具影响力的特征。这有助于简化模型并提高其泛化能力,减少过拟合的风险,并且可以加快模型训练和推理…...
2024Node.js零基础教程(小白友好型),nodejs新手到高手,(六)NodeJS入门——http模块
047_http模块_获取请求行和请求头 hello,大家好,那第二节我们来介绍一下如何在这个服务当中来提取 HTT 请求报文的相关内容。首先先说一下关于报文的提取的方法,我在这个文档当中都已经记录好了,方便大家后续做一个快速的查阅。 …...
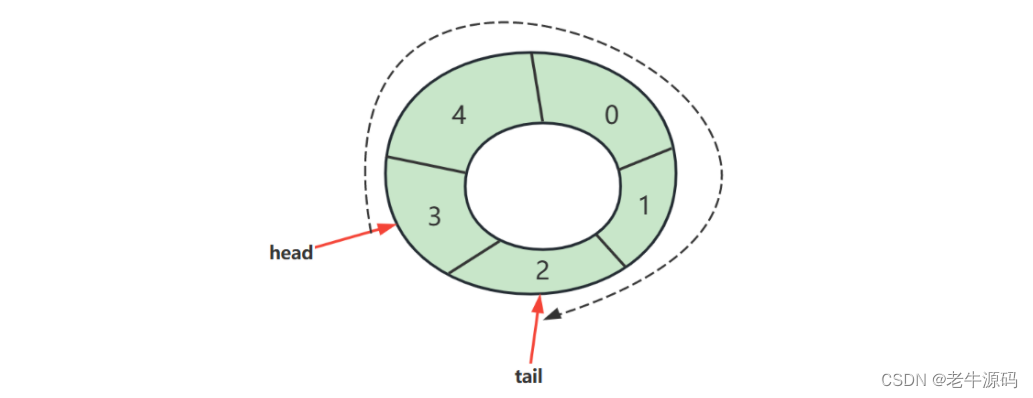
【数据结构与算法】(5)基础数据结构之队列 链表实现、环形数组实现详细代码示例讲解
目录 2.4 队列1) 概述2) 链表实现3) 环形数组实现 2.4 队列 1) 概述 计算机科学中,queue 是以顺序的方式维护的一组数据集合,在一端添加数据,从另一端移除数据。习惯来说,添加的一端称为尾,移除的一端称为头…...
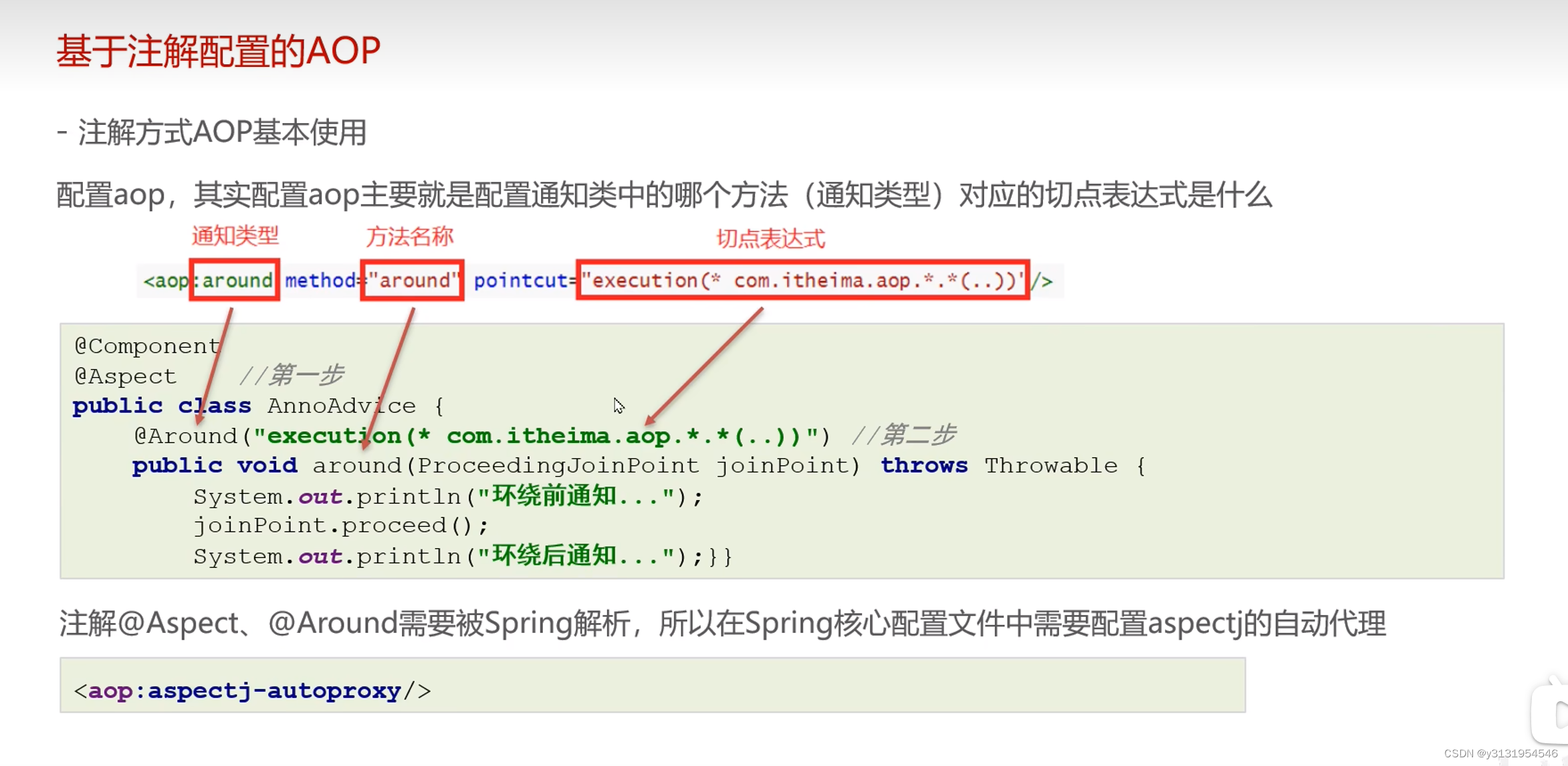
(注解配置AOP)学习Spring的第十七天
基于注解配置的AOP 来看注解式开发 : 先把目标与通知放到Spring里管理 : Service("userService") public class UserServiceImpl implements UserService {Overridepublic void show1() {System.out.println("show1......");}Overridepublic void show2…...

[C++] opencv + qt 创建带滚动条的图像显示窗口代替imshow
在OpenCV中,imshow函数默认情况下是不支持滚动条的。如果想要显示滚动条,可以考虑使用其他库或方法来进行实现。 一种方法是使用Qt库,使用该库可以创建一个带有滚动条的窗口,并在其中显示图像。具体步骤如下: 1&…...
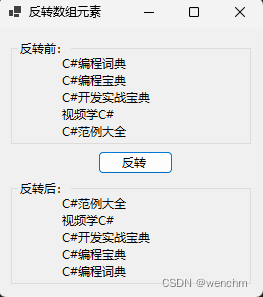
C#用Array类的Reverse方法反转数组中元素
目录 一、Array.Reverse 方法 1.重载 2.Reverse(Array, Int32, Int32) 3. Reverse(Array) 4.Reverse(T[]) 5. Reverse(T[], Int32, Int32) 二、实例 1.Array.Reverse 方法4种重载方法综合实例 2.Reverse(Array)方法的实例 一、Array.Reverse 方法 反转一维 Array 或部…...
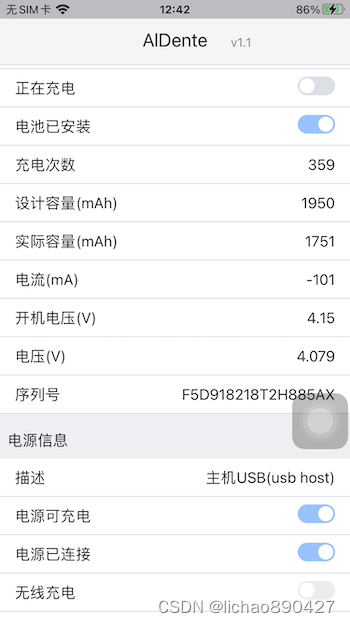
iOS AlDente 1.0自动防过充, 拯救电池健康度
经常玩iOS的朋友可能遇到过长时间过充导致的电池鼓包及健康度下降问题。MacOS上同样会出现该问题,笔者用了4年的MBP上周刚拿去修了,就是因为长期不拔电源的充电,开始还是电量一半的时候不接电源会黑屏无法开机,最后连着电源都无法…...

春晚刘谦魔术——约瑟夫环
昨晚,刘谦在春晚上表演了一个魔术,通过对四张撕成两半的纸牌连续操作,最终实现了纸牌的配对。 这个魔术虽然原理不是很难,但是通过刘谦精湛的表演还是让这个魔术产生了不错的效果(虽然我感觉小尼的效果更不错ÿ…...

itextpdf使用:使用PdfReader添加图片水印
gitee参考代码地址:https://gitee.com/wangtianwen1996/cento-practice/tree/master/src/test/java/com/xiaobai/itextpdf 参考文章:https://www.cnblogs.com/wuxu/p/17371780.html 1、生成带有文字的图片 使用java.awt包的相关类生成带文字的图片&…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
